Determination of 3 D structure avg density total

Determination of 3 D structure, avg density, total mass and plasma properties of an EUV filament observed by So. HO/CDS, So. HO/SUMER and VTT/MSDP Pavol Schwartz Astron. Inst. , Academy of Sci. of the Czech Rep. , Ondřejov, Czech Republic Peter Heinzel Astron. Inst. , Academy of Sci. of the Czech Rep. , Ondřejov, Czech Republic Brigitte Schmieder Observatoire de Paris, Section Meudon, France

Ha filament full-disk observations 15 October 1999 area of CDS observations MEUDON Ha full-disk observations

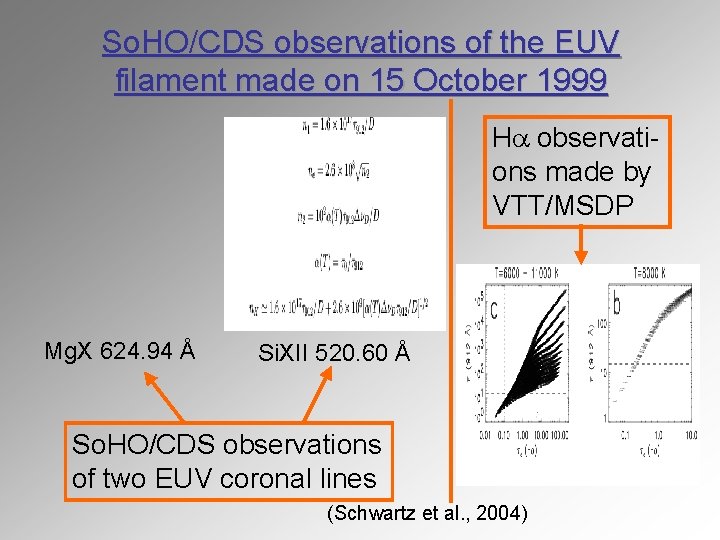
So. HO/CDS observations of the EUV filament made on 15 October 1999 Ha observations made by VTT/MSDP Mg. X 624. 94 Å Si. XII 520. 60 Å So. HO/CDS observations of two EUV coronal lines (Schwartz et al. , 2004)

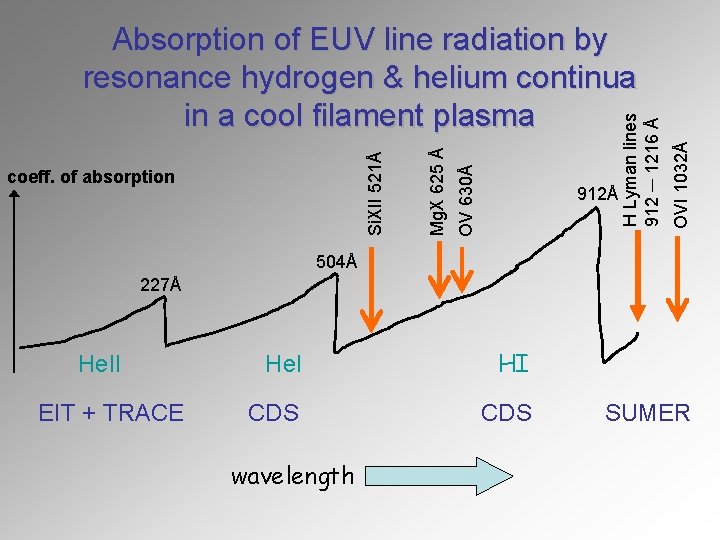
intensity decrease of TR and coronal EUV lines in an EUV filament is caused by: • Absorption by resonance hydrogen & helium continua in a cool filament plasma (coronal and TR lines with wavelengths lower than 912 Å) • volume blocking ─ volume of an EUV filament is not occupied by hot coronal plasma unlike surrounding corona therefore EUV coronal lines are not emitted from this volume

OVI 1032Å 912Å H Lyman lines 912 ─ 1216 Å OV 630Å coeff. of absorption Mg. X 625 Å Si. XII 521Å Absorption of EUV line radiation by resonance hydrogen & helium continua in a cool filament plasma 504Å 227Å He. II EIT + TRACE He. I HI CDS wavelength SUMER

Why are EUV-filaments more extended than their Ha counterparts ? Because opacity in their extensions in EUV is large enough to be observed as dark structures but in Ha is opacity too low. to(Ha) ─ optical thickness at Ha center t(912 Å) ─ optical thickness at H Lyman continuum head dtn=kn dz Ha filament EUV extension (Heinzel et al. , 2001)

Spectroscopic model intensity at height h normalized to quiet-Sun is defined as f(h); e (h) is volume emissivity solar surface quiet-Sun intensity as volume emissivity integrated along whole line of sight intensity emitted from EUV filament is influenced both by absorption and volume blocking the top height of Ha counterpart can be computed from contribution to intensity from corona above this Ha counterpart (Heinzel, Anzer and Schmieder, 2003)

Schwartz et al. (2004) 3 D structure of EUV extension seen from different view angles (t 912=5)

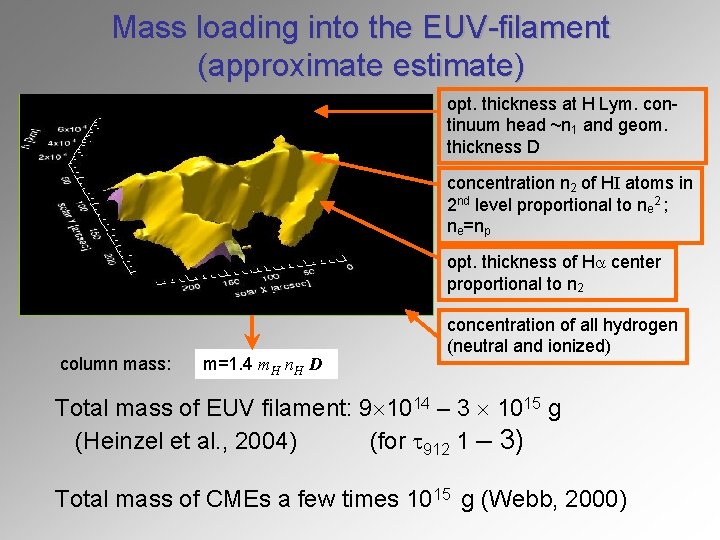
Mass loading into the EUV-filament (approximate estimate) opt. thickness at H Lym. continuum head ~n 1 and geom. thickness D concentration n 2 of HI atoms in 2 nd level proportional to ne 2 ; ne=np opt. thickness of Ha center proportional to n 2 column mass: m=1. 4 m. H n. H D concentration of all hydrogen (neutral and ionized) Total mass of EUV filament: 9 1014 – 3 1015 g (Heinzel et al. , 2004) (for t 912 1 – 3) Total mass of CMEs a few times 1015 g (Webb, 2000)

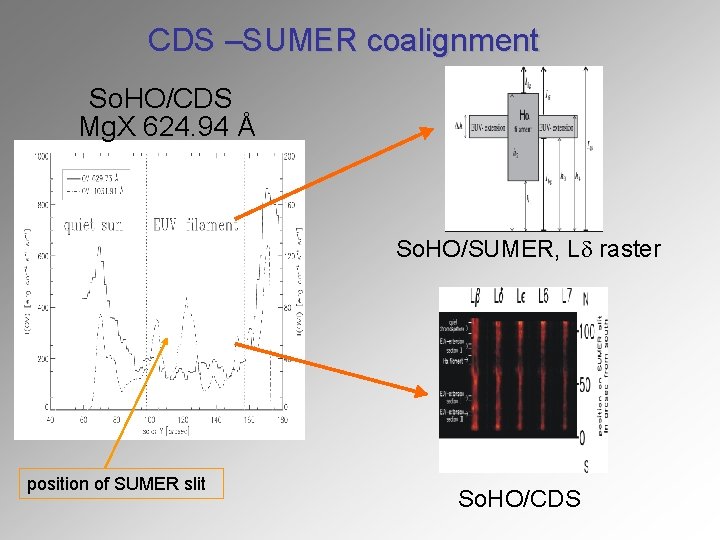
CDS –SUMER coalignment So. HO/CDS Mg. X 624. 94 Å So. HO/SUMER, Ld raster position of SUMER slit So. HO/CDS

So. HO/SUMER OVI & CDS OV observations: verifying the SUMER slit position in CDS raster OV and OVI lines correlate well outside the EUV-filament area

Spectra of hydrogen Lyman lines in the filament and in the chromosphere observed by So. HO/SUMER on 15 Oct 1999 10: 42 ─ 10: 56 UT

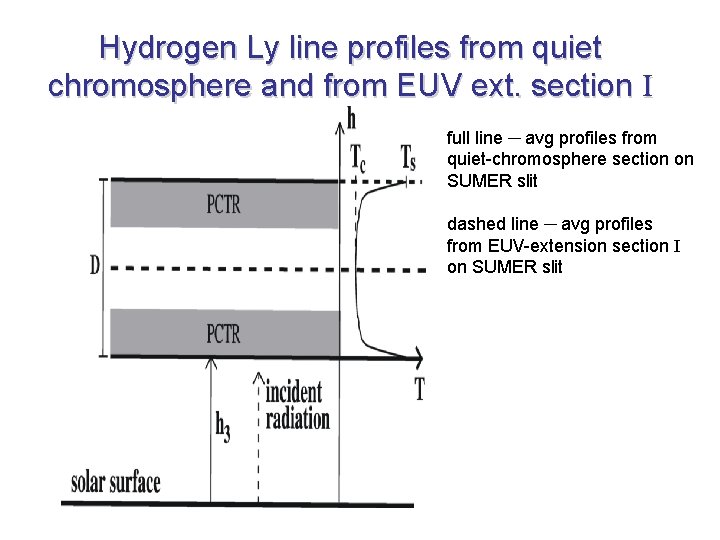
Hydrogen Ly line profiles from quiet chromosphere and from EUV ext. section I full line ─ avg profiles from quiet-chromosphere section on SUMER slit dashed line ─ avg profiles from EUV-extension section I on SUMER slit

1 D-slab model of an filament gas pressure P=const turbulent velocity vt 5 km s-1 (Heinzel, Schmieder and Vial, 1997)

Fitting observed profiles with synthetic profiles § creation of the catalog of synthetic H Lyman profiles using 1 D-slab models with different sets of parameters: h 3 and D known from 3 D structure and vt=5 km s-1 are kept constant. Tc, Ts, factor g of steepness of temperature increase/ decrease in PCTR, P, filling factor are changing. The larger g is the steeper increase/decrease of temperature in PCTRs occurs and the thinner PCTRs are. § search for the best model in catalog by minimization of 2 of observed and synthetic profiles

EUV extension I H ………… h 3 gamma …. . g v_t ……. . . vt fil. fact. …. . . filling factor tau_o(H_alpha) …. to(Ha)

Plasma properties for EUV ext. I across the 1 D-slab model

EUV extension II

EUV extension III

Future plans • compute bigger and more fine grids of models • try to model also profiles from Ha filament ─ we know only top height of Ha filament therefore its geometrical thickness cannot be estimated • use Levenberg-Marquart method for 2 minimization ─ 2 assumptions: computer cluster and need to rewrite code for parallelization • More realistic models with more fine structure ─ fibers approximated by multiple 1 D slabs

The END