Determinan dan Invers Determinan suatu matriks A didefinisikan

Determinan dan Invers Determinan suatu matriks A didefinisikan sebagai : Determinan (aij) = aij = Invers aij = cij = (-1)i+j. Mij contoh : Berapakah nilai x 1, x 2 dan x 3 dari sistem persamaan berikut : x 1 + 0, 5 x 2 2 x 1 + x 2 + x 3 0, 5 x 1 + 0, 5 x 2 + x 3 = 100 = 200 = 100

Dalam bentuk matriks : invers: Determinan ; = 1, 0 (1, 0– 0, 5) – 0, 5(2, 0– 0, 5) + 0 = 0, 25 cij c 11 c 12 c 13 c 21 c 22 c 23 c 31 c 32 c 33 = (-1). M ij = 1(1, 0 - 0, 5) = -1(2, 0 - 0, 5) = 1(1, 0 - 0, 5) = -1(0, 5 – 0) = 1(1, 0 - 0) = -1(0, 5 – 0, 25) = 1(0, 5 – 0) = -1(1, 0 – 0) = 1(1, 0 – 1, 0) = 0, 5 = -1, 5 = 0, 5 = -0, 5 = 1, 0 = -0, 25 = 0, 5 = -1, 0 =0

nilai xj : jadi : x 1 = 0; x 2 = 200, dan x 3 = 0

Eliminasi gauss Prosedur penyelesaian dari metoda ini adalah mengurangi sistem persamaan ke dalam bentuk segitiga sedemikian sehingga salah satu dari persamaan-persamaan tersebut hanya mengandung satu bilangan tak diketahui, dan setiap persamaan berikutnya hanya terdiri dari satu tambahan bilangan tak diketahui baru

Contoh : Selesaikan sistem persamaan berikut ini: 3 x - 0. 1 y – 0. 2 z = 7. 85 0. 1 x + 7 y – 0. 3 z = -19. 3 0. 3 x – 0. 2 y + 10 z = 71. 4 Dalam bentuk matriks :

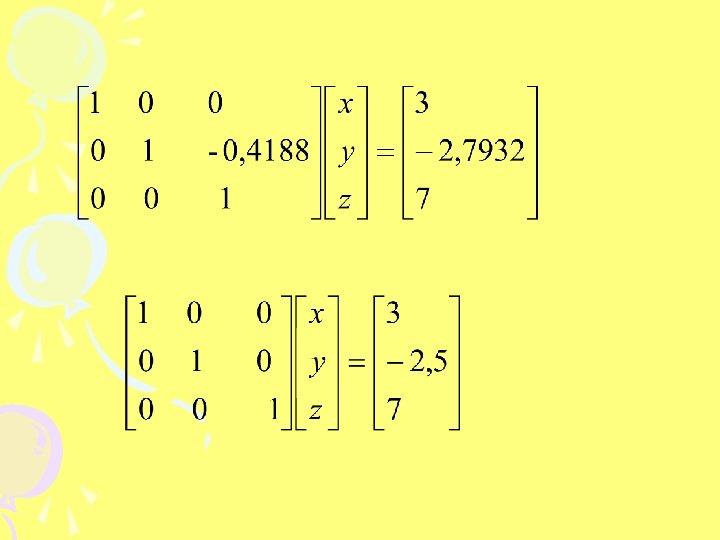
Metode Gauss Jordan • Metode Gauss jordan adalah pengembangan dari eliminasi gauss • Matriks di rubah menjadi segitiga bawah dan atas (matriks identitas) • Variabel persamaan bisa langsung dibaca

Contoh : Selesaikan sistem persamaan berikut ini: 3 x - 0. 1 y – 0. 2 z = 7. 85 0. 1 x + 7 y – 0. 3 z = -19. 3 0. 3 x – 0. 2 y + 10 z = 71. 4 Dalam bentuk matriks :

Metode Gauss Seidel • Meode ini menerapkan terkaan-terkaan awal dan kemudian diiterasi untuk memperoleh taksiran-taksiran yang diperhalus dari penyelesaiannya Contoh : Selesaikan sistem persamaan berikut ini: 3 x - 0. 1 y – 0. 2 z = 7. 85 0. 1 x + 7 y - 0. 3 z = -19. 3 0. 3 x – 0. 2 y + 10 z = 71. 4

prosedur : ØNilai yang belum diketahui dianggap nol ØHasil dari perhitungan digunakan untuk perhitungan selanjutnya. v. Iterasi pertama ØDengan menganggap bahwa y dan z adalah nol, maka x dapat dihitung:

Nilai y ini dengan anggapan nilai z adalah nol dan x adalah hasil yang barus saja dididapat, kemudian disubtitusikan ke persamaan berikut : Nilai y dan nilai x , disubtitusikan untuk mencari nilai z

v. Iterasi ke-2

v. Iterasi ke-3

v. Iterasi ke-4