Detection Limits All instrumental methods have a degree

When a graphical display of results is obtained, the detection limit of the instrument

Peak-to-peak noise level as a basis for detection limit. A “detectable” analyte signal would

2. Detection Limit is the concentration that gives a signal three times the standard

Example A blank solution in a colorimetric analysis resulted in absorbance readings of 0.

The net reading of the standard = 0. 051 – 0. 004 = 0.

Review of Fundamental Concepts Formula Weight It is assumed that you can calculate the

Assuming approximate atomic weights of 1. 00, 16. 00, 23. 00, 35. 5, and

In the same manner, the number of mmol of a substance contained in a

The number of mmol of Na 2 WO 4 (FW = 293. 8 mg/mmol)

The number of mg contained in 0. 25 mmol of Fe 2 O 3

Calculations Involving Solutions Molarity (M) Molarity of a solution can be defined as the

Calculations Involving Molarity = mol/L = mmol/m. L This can be further formulated as

Find the molarity of a solution resulting from dissolving 1. 26 g of Ag.

We can find the molarity directly in one step using dimensional analysis ? mol

Let us find the number of mg of Na. Cl per m. L of

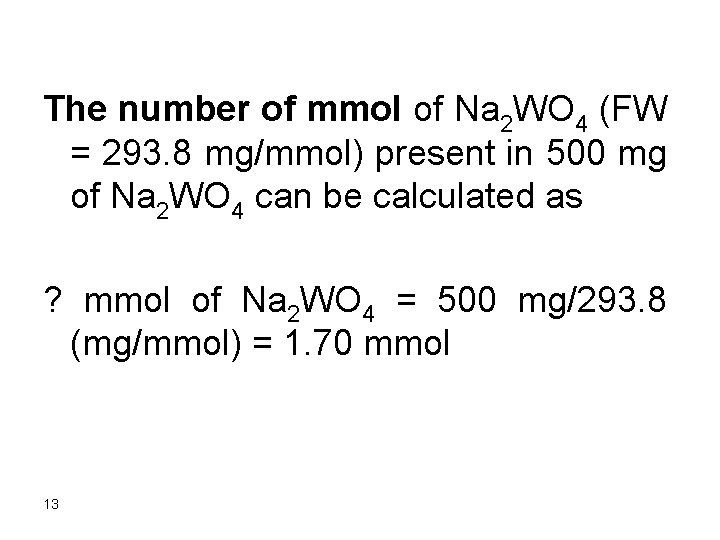
Slides: 19

Download presentation

Detection Limits All instrumental methods have a degree of noise associated with the measurement that limits the amount of analyte that can be detected. 1. Detection Limit is the lowest concentration level that can be determined to be statistically different from an analyte blank. 1

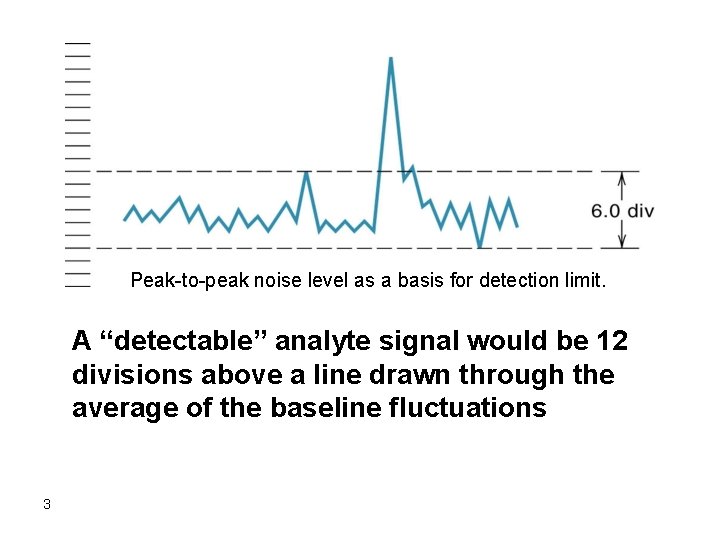
When a graphical display of results is obtained, the detection limit of the instrument can be defined as the concentration of analyte resulting in a signal that is twice as the peak to peak noise (the distance between the two dashed lines in the schematic below). 2

Peak-to-peak noise level as a basis for detection limit. A “detectable” analyte signal would be 12 divisions above a line drawn through the average of the baseline fluctuations 3

2. Detection Limit is the concentration that gives a signal three times the standard deviation of the background signal. To calculate the detection limit: a. Find the average of the blank signal b. Find the standard deviation of the blank c. Find the net analyte signal DL = 4 analyte conc. * 3*s analyte signal

Example A blank solution in a colorimetric analysis resulted in absorbance readings of 0. 000, 0. 008, 0. 006, and 0. 003. A 1 ppm standard solution of the analyte resulted in a reading of 0. 051. Calculate the detection limit. The standard deviation of the four data points of the blank can be calculated to be + 0. 0032 and the mean of the blank is 0. 004 5

The net reading of the standard = 0. 051 – 0. 004 = 0. 047 The detection limit is the concentration which results in three times the standard deviation (3 x 0. 0032 = 0. 0096). Detection limits = 1 ppm x 0. 0096/0. 047 = 0. 2 ppm The absorbance reading of the least detectable concentration = 0. 0096 + 0. 004 = 0. 014 6

Stoichiometric Calculations 7

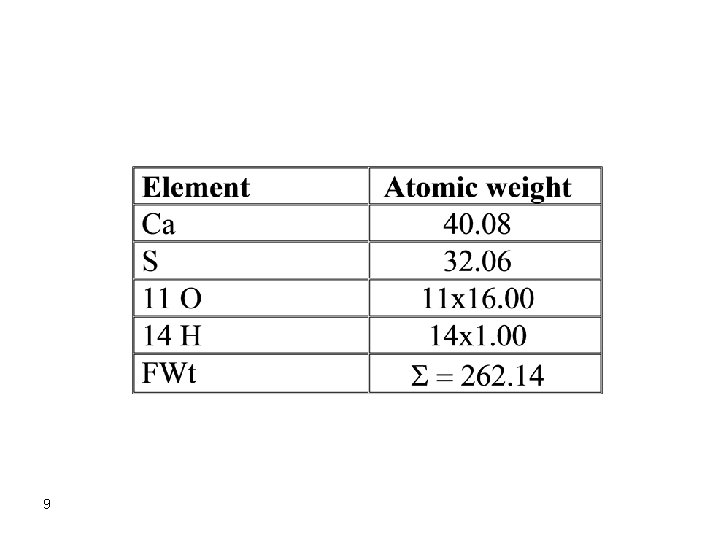
Review of Fundamental Concepts Formula Weight It is assumed that you can calculate the formula or molecular weights of compounds from respective atomic weights of the elements forming these compounds. The formula weight (FW) of a substance is the sum of the atomic weights of the elements from which this substance is formed from. The formula weight of Ca. SO 4. 7 H 2 O is 8

The Mole 10

Assuming approximate atomic weights of 1. 00, 16. 00, 23. 00, 35. 5, and 12. 00 atomic mass units for hydrogen, oxygen, sodium, chlorine atom, and carbon, respectively. The number of moles contained in a specific mass of a substance can be calculated as: mol = g substance/FW substance The unit for the formula weight is g/mol 11

In the same manner, the number of mmol of a substance contained in a specific weight of the substance can be calculated as mmol = mol/1000 Or, mmol = mg substance/FW substance 12

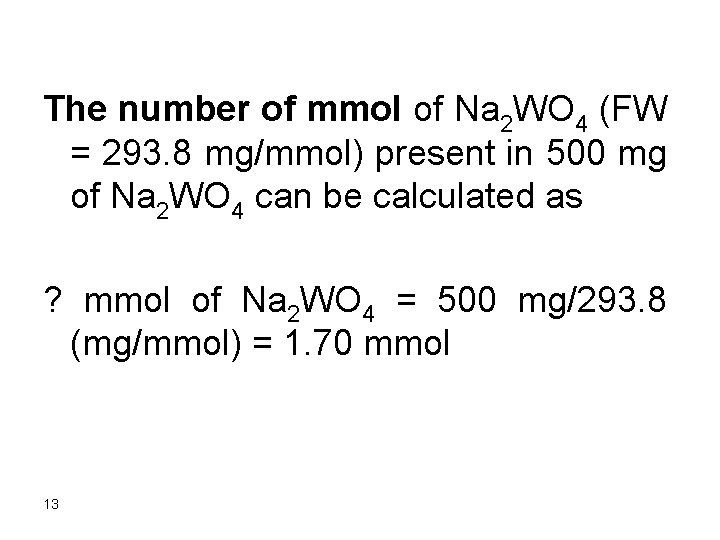
The number of mmol of Na 2 WO 4 (FW = 293. 8 mg/mmol) present in 500 mg of Na 2 WO 4 can be calculated as ? mmol of Na 2 WO 4 = 500 mg/293. 8 (mg/mmol) = 1. 70 mmol 13

The number of mg contained in 0. 25 mmol of Fe 2 O 3 (FW = 159. 7 mg/mmol) can be calculated as ? mg Fe 2 O 3 = 0. 25 mmol Fe 2 O 3 x 159. 7 (mg/mmol) = 39. 9 mg Therefore, either the number of mg of a substance can be obtained from its mmols or vice versa. 14

Calculations Involving Solutions Molarity (M) Molarity of a solution can be defined as the number of moles of solute dissolved n 1 L of solution. This means that 1 mol of solute will be dissolved in some amount of water and the volume will be adjusted to 1 L. The amount of water may be less than 1 L as the final volume of solute and water is exactly 1 L. 15

Calculations Involving Molarity = mol/L = mmol/m. L This can be further formulated as Number of moles = Molarity X volume in Liters, or mol = M (mol/L) x VL Number of mmol = Molarity x volume in m. L , or mmol = M (mmol/m. L) x Vm. L 16

Find the molarity of a solution resulting from dissolving 1. 26 g of Ag. NO 3 (FW = 169. 9 g/mol) in a total volume of 250 m. L solution. First find mol Ag. NO 3 = 1. 26 g Ag. NO 3 / 169. 9 g/mol = 7. 42 x 10 -3 mol Also you should know that 250 m. L = 0. 25 L Now one can calculate the molarity directly from Molarity = mol/L M = 7. 42 x 10 -3 mol/0. 25 L = 0. 0297 mol/L 17

We can find the molarity directly in one step using dimensional analysis ? mol Ag. NO 3 / L = (1. 26 g Ag. NO 3 / 250 m. L) x ( mol Ag. NO 3/169. 9 g Ag. NO 3) x (1000 m. L/1 L) =0. 0297 M 18

Let us find the number of mg of Na. Cl per m. L of a 0. 25 M Na. Cl solution First we should be able to recognize the molarity as 0. 25 mol/L or 0. 25 mmol/m. L. Of course, the second term offers what we need directly ? mg Na. Cl in 1 m. L = (0. 25 mmol Na. Cl/m. L) x (58. 5 mg Na. Cl/mmol Na. Cl) = 14. 6 mg Na. Cl/m. L 19