Detecting threedimensional magnetic reconnection in Earths magnetosphere John

Detecting three-dimensional magnetic reconnection in Earth’s magnetosphere John C. Dorelli NASA/GSFC 1. Magnetic geometry and topology are weakly coupled in three dimensions; what are the implications for spacecraft observations or reconnection signatures? 2. Can we use simultaneous magnetic field observations at multiple spacecraft to detect three-dimensional magnetic nulls? Collaborators: Joo Hwang (NASA/GSFC) Melvyn Goldstein (NASA/GSFC)

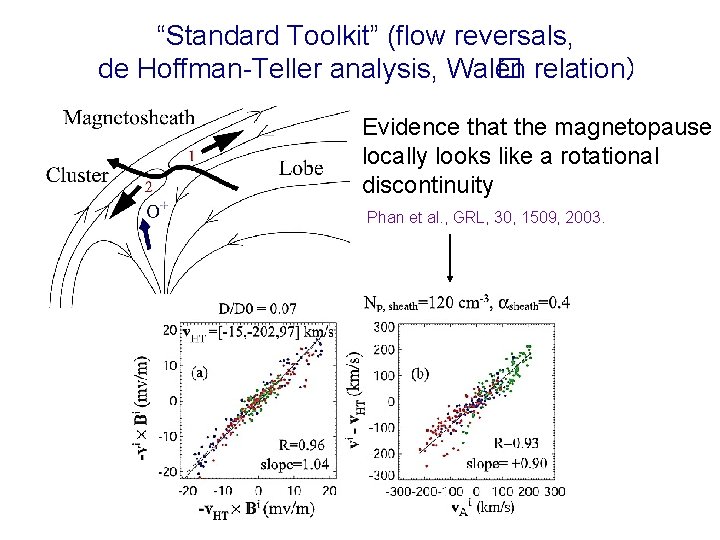
“Standard Toolkit” (flow reversals, de Hoffman-Teller analysis, Wal� én relation) Evidence that the magnetopause locally looks like a rotational discontinuity Phan et al. , GRL, 30, 1509, 2003.

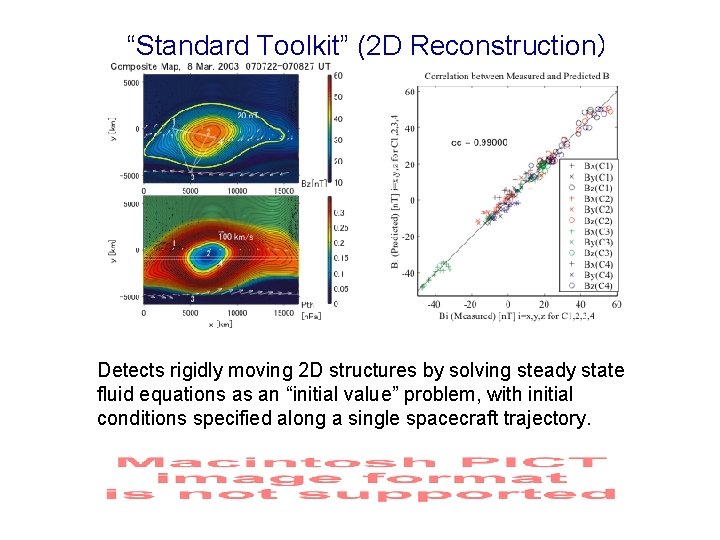
“Standard Toolkit” (2 D Reconstruction) Detects rigidly moving 2 D structures by solving steady state fluid equations as an “initial value” problem, with initial conditions specified along a single spacecraft trajectory.

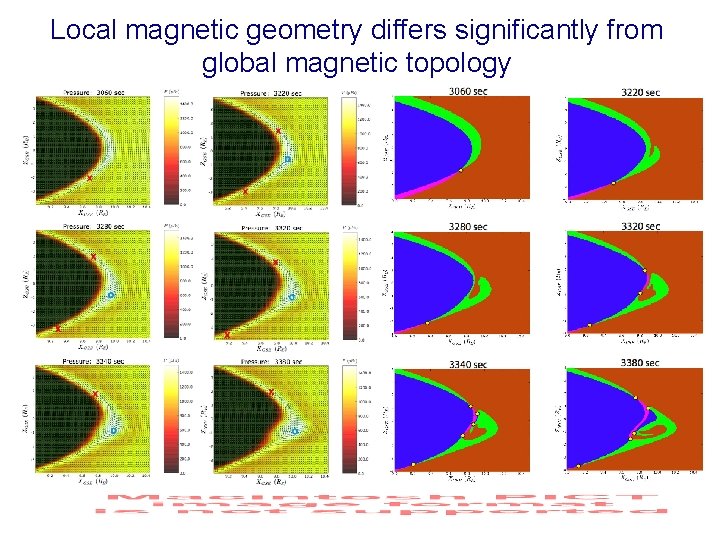
Local magnetic geometry differs significantly from global magnetic topology

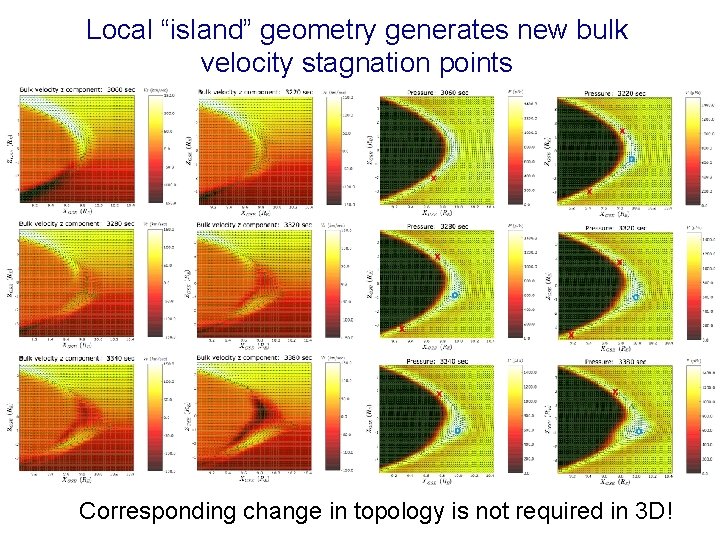
Local “island” geometry generates new bulk velocity stagnation points Corresponding change in topology is not required in 3 D!

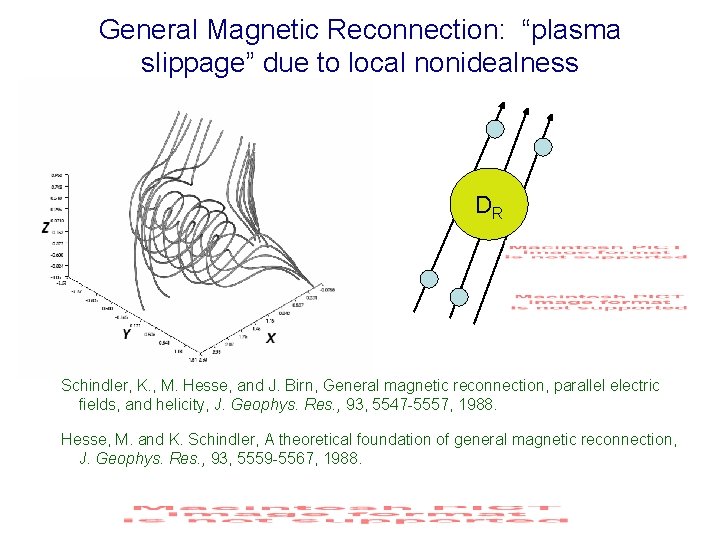
General Magnetic Reconnection: “plasma slippage” due to local nonidealness DR Schindler, K. , M. Hesse, and J. Birn, General magnetic reconnection, parallel electric fields, and helicity, J. Geophys. Res. , 93, 5547 -5557, 1988. Hesse, M. and K. Schindler, A theoretical foundation of general magnetic reconnection, J. Geophys. Res. , 93, 5559 -5567, 1988.

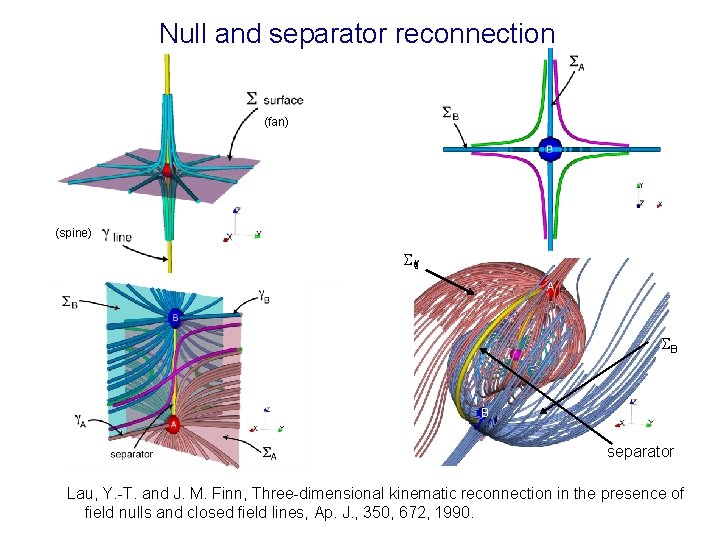
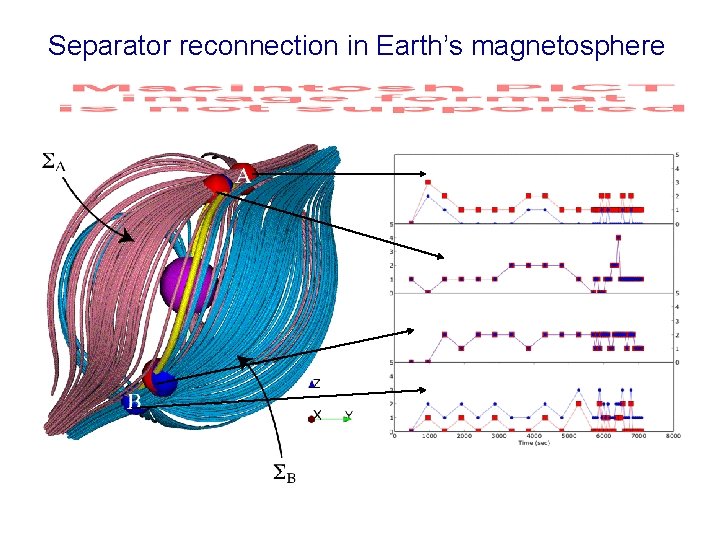
Null and separator reconnection (fan) (spine) A B B separator Lau, Y. -T. and J. M. Finn, Three-dimensional kinematic reconnection in the presence of field nulls and closed field lines, Ap. J. , 350, 672, 1990.

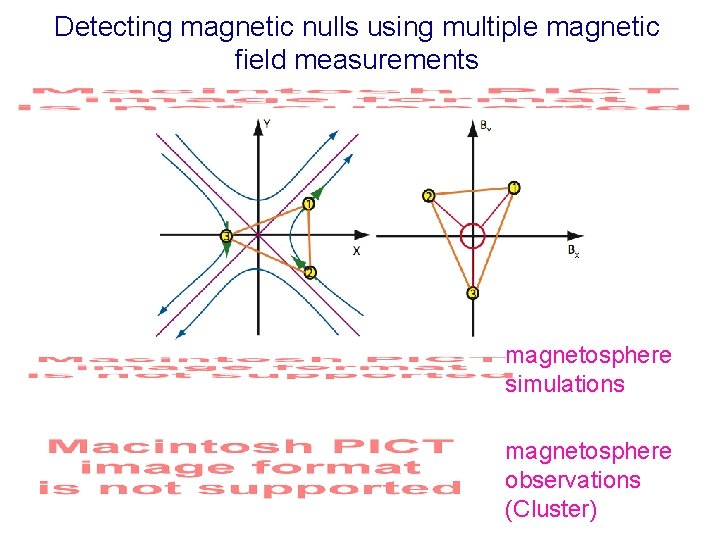
Detecting magnetic nulls using multiple magnetic field measurements magnetosphere simulations magnetosphere observations (Cluster)

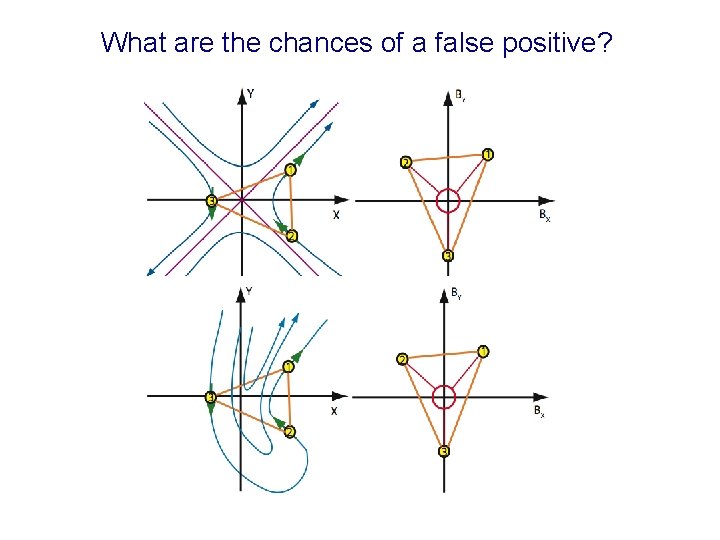
What are the chances of a false positive?

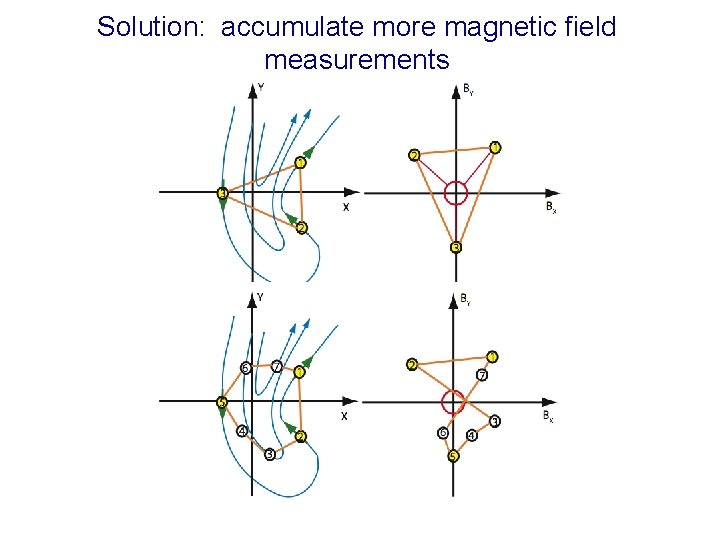
Solution: accumulate more magnetic field measurements

An improved null detection algorithm 1. Accumulate high time resolution magnetic field measurements at the four Cluster spacecraft over some time interval T. 2. Compute the convex hull of the field measurement locations in a coordinate system defined by identifying the motion of a coherent magnetic structure (e. g. , Shi et al. , Motion of observed structures calculated from multi-point magnetic field measurements: Application to Cluster, Geophys. Res. Lett. , 33, L 08109, doi: 10. 1029/2005 GL 025073, 2006. ) 3. Triangulate the hull computed in step 2. 4. Map the triangles computed in step 3 to three-dimensional magnetic field space (“B-space”). 5. Apply Greene’s algorithm to the ordered sequence of B-space triangles computed in step 4.

Separator reconnection in Earth’s magnetosphere

Summary 1. Magnetic geometry and topology are weakly coupled in three dimensions (particularly in non-toroidal systems like Earth’s magnetosphere); thus, spacecraft analysis techniques (“Standard Toolkit”) which are designed to detect interesting local geometrical consequences of magnetic reconnection will likely miss important global topological features of reconnection. 2. Existing techniques for detecting/reconstructing magnetic nulls suffer from a sparse data problem (not enough data to rule out alternative magnetic topologies). 3. It should be straightforward to improve the existing null detection algorithms by: 1) establishing a coordinate system for moving coherent magnetic structures, 2) accumulating more magnetic field observations. 4. We are currently testing the Improved Null Detection Algorithm on simulations; applications to Cluster data will soon follow.