Detecting the Inferior Thoracic Aperture using Statistical Shape

Outline • Introduction – What is the Inferior Thoracic Aperture (ITA)? – Why segment

Inferior Thoracic Aperture • 3 D closed contour. • Near the periphery of human

Relation to Diaphragm • Diaphragm hangs off the ITA. • Diaphragm related to normal

Difficulty • Diaphragm hangs off the ITA. • Difference between ITA and boundary of

Partitioning ITA shape • • Two parts A and C. A >> easy to

Additional points considered • • • (1, 2) ends of Xiphoid process. (3, 4,

Identifying Landmarks • B >> Known corresponding landmarks. • A, C >> Landmark sliding

Identifying Landmarks • Initial rough correspondence – Equal distance sampling of A and C.

Constructing PDM • • • Set of training shapes. Find corresponding landmarks on each.

Detecting the ITA • v is the set of landmarks along shape to be

Detecting landmarks along A, B • B >> anatomic landmarks, easy to extract. •

Mahalanobis distance • D = (v - m)TS-1(v - m) • D = (v.

Experiments • 14 shapes. • Leave one out. • e 1 = average distance

Results • Better than direct interpolation.

Conclusion • A new method to detect the Inferior Thoracic Aperture. • Better performance

Slides: 20

Download presentation

Detecting the Inferior Thoracic Aperture using Statistical Shape Models Pahal Dalal Department of Computer Science & Engineering, University of South Carolina

Outline • Introduction – What is the Inferior Thoracic Aperture (ITA)? – Why segment the ITA? – Why is segmenting the ITA difficult? • Construction of Shape Model • Detecting the ITA • Conclusion

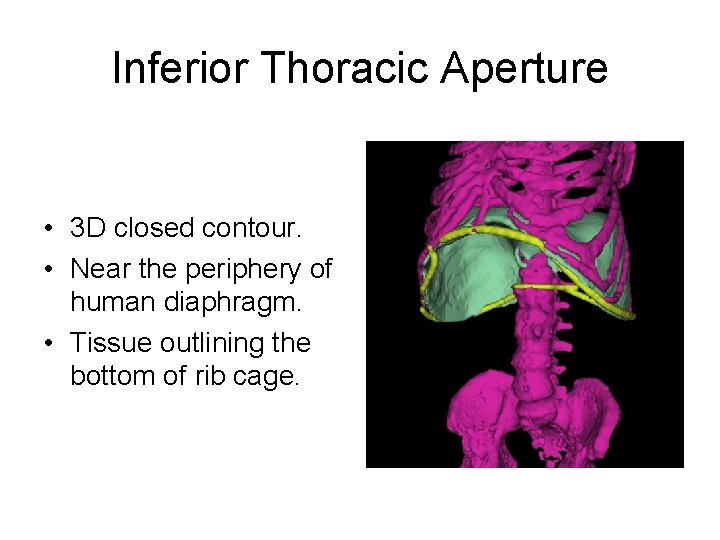
Inferior Thoracic Aperture • 3 D closed contour. • Near the periphery of human diaphragm. • Tissue outlining the bottom of rib cage.

Relation to Diaphragm • Diaphragm hangs off the ITA. • Diaphragm related to normal pulmonary function. • Extracting ITA can help extract diaphragm.

Difficulty • Diaphragm hangs off the ITA. • Difference between ITA and boundary of diaphragm difficult to find. • CT images very fuzzy in certain parts.

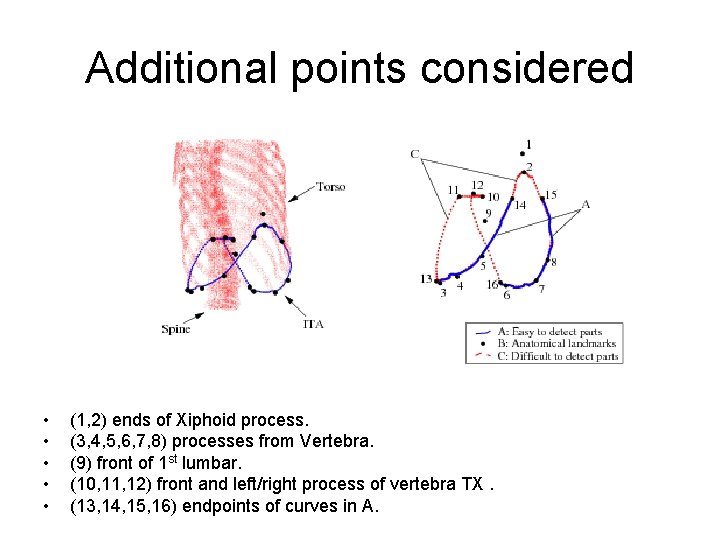
Partitioning ITA shape • • Two parts A and C. A >> easy to extract. C >> difficult to extract. B >> additional anatomical points on/near ITA.

Additional points considered • • • (1, 2) ends of Xiphoid process. (3, 4, 5, 6, 7, 8) processes from Vertebra. (9) front of 1 st lumbar. (10, 11, 12) front and left/right process of vertebra TX. (13, 14, 15, 16) endpoints of curves in A.

Identifying Landmarks • B >> Known corresponding landmarks. • A, C >> Landmark sliding approach. • Wang, S. , Kubota, T. , Richardson, T. : Shape correspondence through landmark sliding. In: CVPR. (2004) I– 143– 150

Identifying Landmarks • Initial rough correspondence – Equal distance sampling of A and C. • Refinement – Thin Plate Spline Bending Energy. – Landmark Sliding. – Strict partitioning enforced.

Constructing PDM • • • Set of training shapes. Find corresponding landmarks on each. Mean shape >> m. Co-variance >> S. Shape model >> (m, S).

Detecting the ITA • v is the set of landmarks along shape to be found. • m = [ m. P m. Q ] • v = [ v. P v. Q ] • P >> landmarks along A and B. • Q >> landmarks along C.

Detecting landmarks along A, B • B >> anatomic landmarks, easy to extract. • A >> easy to extract. • Landmark sliding approach. • m. P used as template landmarks. • Gives v. P.

Mahalanobis distance • D = (v - m)TS-1(v - m) • D = (v. Q m. Q)S 4(v. Q- m. Q) +2(v. P - m. P)TS 2(v. Q- m. Q) +k • Partial derivative = 0 • v. Q = m. Q - S 4 -1 S 2(v. P - m. P) • Interpolate landmarks along A and C to obtain complete shape.

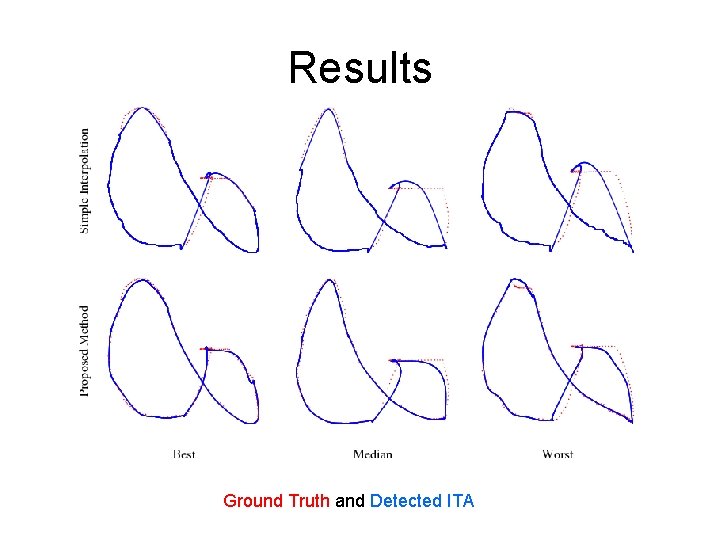
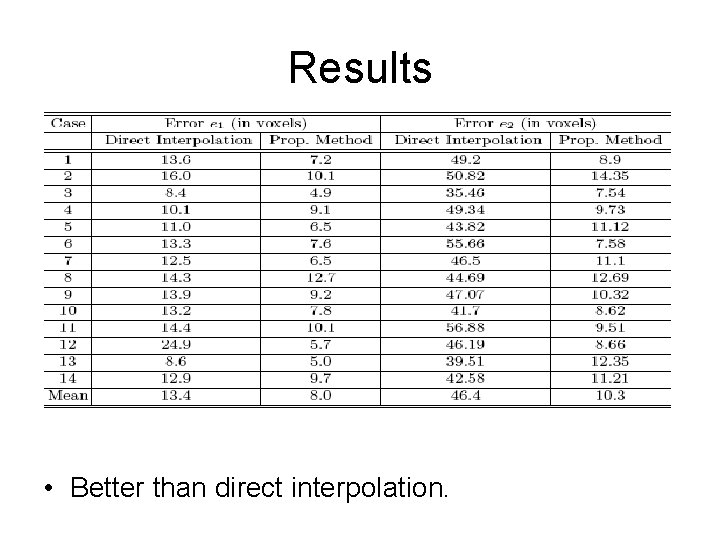
Experiments • 14 shapes. • Leave one out. • e 1 = average distance between predicted shape and truth. • e 2 = average distance between predicted landmark and truth landmark.

Results Ground Truth and Detected ITA

Results • Better than direct interpolation.

Conclusion • A new method to detect the Inferior Thoracic Aperture. • Better performance than direct interpolation.

Questions?