Designing Programs that Check Their Work Manuel Blum

Designing Programs that Check Their Work Manuel Blum Sampath Kannan by Jeffrey Corbell

Overview • • • Introduction to a Program Checker Other Methods of Determining Correctness Definition of a Program Checker Example of a Checker: Graph Isomorphism Beigel’s Theorem

What is a program checker • Program that checks the output of a program to determine if the program is correct or buggy Formally: – P and C are programs, I is the input – For any I run on P, C is run and determines whether P is correct for I or buggy

Other Methods of Determining Correctness • Program verification – Use a proof to prove a program is correct – Very difficult to do – Argued that it doesn't improve confidence in correctness • very complex • may contain errors which would be difficult to detect

Other Methods of Determining Correctness • Program testing – Run program on input that you know the correct output for – Compare program output to expected output – Problems • No general way to create test data • No theorems to describe behavior if they do pass tests

Differences Between a Checker and Testing • A checker is a program that uses its own algorithm that allows it to check the output • Program testing usually only uses a small amount of predetermined cases for specific input

Definition of a Bug • Let π represent a decision or search problem • x represents an input to π with π(x) representing the output • P is a deterministic program that supposedly solves π P has a bug if for some instance x of π P(x) ≠ π(x)

Definition of a Checker • Let Cπ be the checker, k be the number of different cases the checker tries, and I be the group of test inputs • CπP(I, k) is the output of the checker and follows these conditions: 1. If P(x) = π(x), then with probability ≥ 1 - 1/2 k CπP(I, k) = CORRECT 2. If P(x) ≠ π(x), then with probability ≥ 1 - 1/2 k CπP(I, k) = BUGGY

Definition of a Checker • However, if P has bugs but P(I)=π(I) then CπP(I, k) may output either CORRECT or BUGGY

Definition of a Checker • Assumed P halts on all inputs • Not always the case • If P(x) exceeds a predetermined bound then the checker should raise a flag, CπP(I, k) = TIME

Definition of a Checker • Runtime includes the time it takes to submit input and receive output from P • Does not include the time it takes P to run

Definition of a Checker • If a checker is a program, how can you be sure the checker is correct? • You can’t really • Checker must have the little oh property with respect to the runtime of P – Ensures the checker is programmed differently than the original program

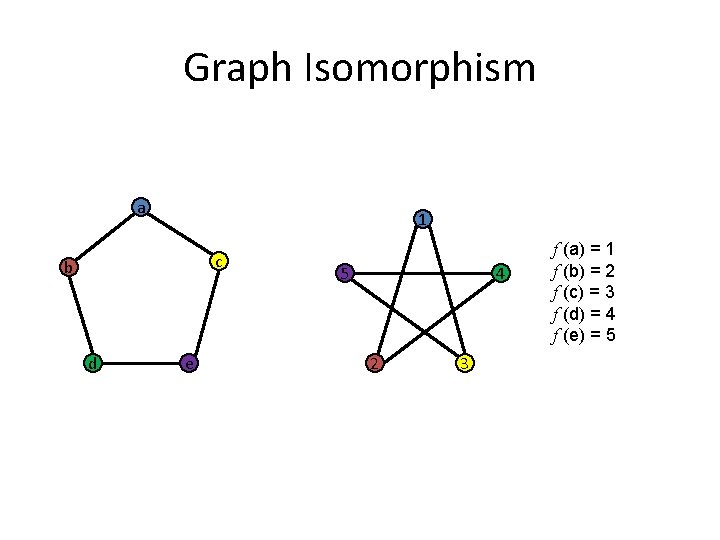
Graph Isomorphism a 1 c b d e 5 4 2 3 f (a) = 1 f (b) = 2 f (c) = 3 f (d) = 4 f (e) = 5

Graph Isomorphism Checker • Let P be a program that solves graph isomorphism – Input: two graphs G and H – Output: YES if G is isomorphic to H; NO otherwise • CGIP(G, H, k) checks P on input G and H

Graph Isomorphism Checker • Compute P(G, H) • If P(G, H)=YES then – Use P to search for an isomorphism from G to H – Check if the resulting correspondence is an isomorphism – If not, return BUGGY; if yes, return CORRECT

Graph Isomorphism Checker • If P(G, H)=NO then – Do k times: • Toss a fair coin • If coin = heads then – Generate a random permutation G’ of G – Compute P(G, G’) – If P(G, G’)=NO then return BUGGY • Return CORRECT • If coin = tails then – Generate a random permutation H’ of H – Compute P(G, H’) – If P(G, H’)=YES then return BUGGY

Graph Isomorphism Checker • CGIP runs in polynomial time • If P has no bugs and G is isomorphic to H, then CGIP(G, H, k) creates an isomorphism from G to H and outputs CORRECT • If P has no bugs and G is not isomorphic to H, then CGIP(G, H, k) tosses coins. It discovers P(G, G’)=YES for all G’ and P(G, H’) for all H’ so outputs CORRECT

Graph Isomorphism Checker • If P(G, H) is incorrect then there are two cases: – If P(G, H)=YES but G is not isomorphic to H, then CGIP fails to construct an isomorphism and outputs BUGGY – If P(G, H)=NO but G is isomorphic to H, the only way that C will return CORRECT is if P(G, G’)= YES if the coin is heads and P(G, H’)= NO when it is tails. But G and H are permuted randomly to produce G’ and H’. Therefore P correctly distinguishes G’ from H’ only by chance for just 1 of 2 k possible sequences

Beigel’s Theorem • Let π1 and π2 be two polynomial-time equivalent decision problems. Then from any polynomial time checker for π1 it is possible to construct a polynomial-time checker for π2.

Beigel’s Theorem • Have a checker Cπ1 for π1 and a program P 2 for π2 • Also have two way polynomial time transformations f 1, 2 and f 2, 1 • This gives us a program for π1 – P 1(x) =P 2(f 1, 2(x))

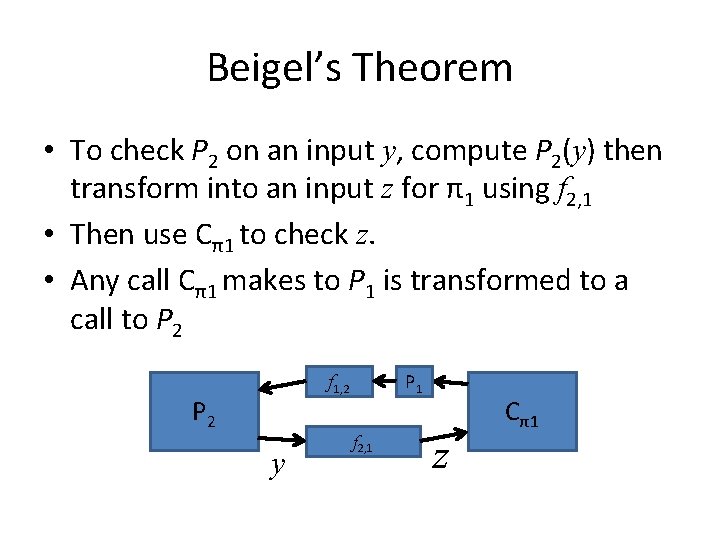
Beigel’s Theorem • To check P 2 on an input y, compute P 2(y) then transform into an input z for π1 using f 2, 1 • Then use Cπ1 to check z. • Any call Cπ1 makes to P 1 is transformed to a call to P 2 P 1 f 1, 2 P 2 y f 2, 1 Cπ1 z

Beigel’s Theorem • If P 2 is correct then P 1 will be correct because P 1 is defined in terms of P 2 • Thus if P 1 is correct on z then P 2 is correct on y • If P 2 is wrong on y and P 1 is correct on z then there’s a contradiction because P 2(y)=P 1(z) • If P 1 is wrong on z then the checker Cπ1 will catch it

Beigel’s Theorem • This checker for π2 runs in polynomial time – Running the checker for π1 – One transformation of f 2, 1 – Polynomial number of applications of f 1, 2

Bibliography • Designing programs that check their work - M. Blum and S. Kannan • Social Processes and Proofs of Theorems and Programs - R. A. De Millo, R. J. Lipton, and A. J. Perlis. • Introduction to the Theory of Computation – M. Sipser • www. wikipedia. org