Designing Hash Tables Sections 5 3 5 4

Designing Hash Tables • Sections 5. 3, 5. 4, 5. 5 1

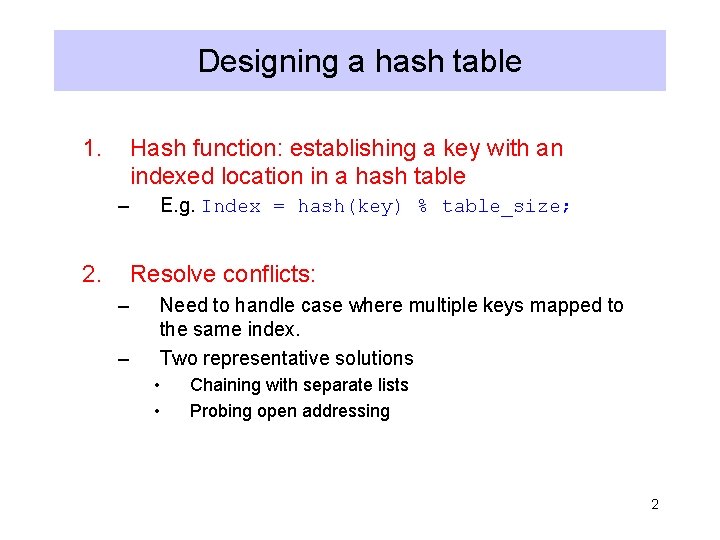
Designing a hash table 1. Hash function: establishing a key with an indexed location in a hash table – 2. E. g. Index = hash(key) % table_size; Resolve conflicts: – – Need to handle case where multiple keys mapped to the same index. Two representative solutions • • Chaining with separate lists Probing open addressing 2

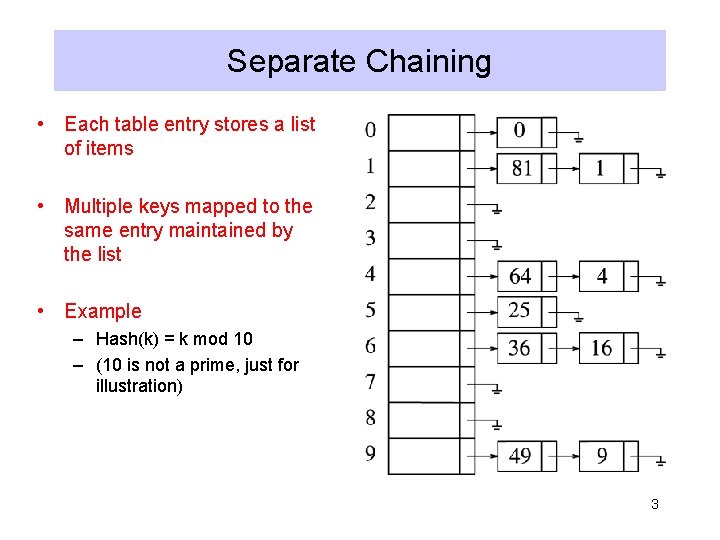
Separate Chaining • Each table entry stores a list of items • Multiple keys mapped to the same entry maintained by the list • Example – Hash(k) = k mod 10 – (10 is not a prime, just for illustration) 3

Separate Chaining Implementation Type Declaration for Separate Chaining Hash Table 4

Hashed. Obj • Needs to provide – Hash function • Provided for string and int (the two non-member functions) – Equality operators (operator== or operator!= ) 5

An example class for Hashed. Obj 6

Chaining 7

Chaining (contd. ) 8

Chaining (contd. ) 9

Analysis of Chaining • Consider an array of size M with N records – Worst case insert without uniqueness check = O(1) • Find location to insert and push_back/front – Worst case remove/find/unique insert = O(N) – Expected case unique insert/find/remove • 1 + O(N/M) – Let us resize the table is N/M exceeds some constant – Expected time = 1 + O( ) = O(1) 10

Hash Tables Without Chaining • Try to avoid buckets with separate lists • How use Probing Hash Tables – If collision occurs, try another cell in the hash table. – More formally, try cells h 0(x), h 1(x), h 2(x), h 3(x)… in succession until a free cell is found. • hi(x) = hash(x) + f(i) • And f(0) = 0 11

Linear Probing • f(i)=i Insert (assume no duplicated keys) 1. 2. 3. Index = hash(key) % table_size; If table[index] is empty, put information (key and others) in entry table[index]. If table[index] is not empty then Index ++; index = index % table_size; goto 2. Search (key) 1. 2. 3. 4. Index = hash(key) % table_size; If (table[index] is empty) return – 1 (not found). Else if (table[index]. key == key) return index; Index ++; index = index % table_size; goto 2. 12

Example Insert 89, 18, 49, 58, 69 (hash(k) = k mod 10) 13

Linear probing • Delete – Can be tricky, must maintain the consistency of the hash table. – What is the simplest deletion strategy you can think of? ? 14

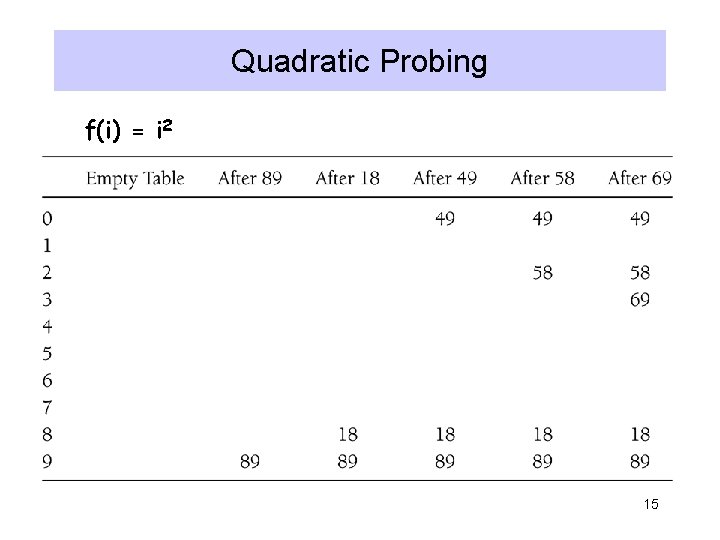
Quadratic Probing f(i) = i 2 15

Probing strategy hash table 16

Double Hashing • f(i) = i*hash 2(x) • E. g. hash 2(x) = 7 – (x % 7) What if hash 2(x) = 0 for some x? 17

Analysis of Hash Table Without Chaining • Expected case analysis of insertion into a table of size M containing n records – i=1 i probability of trying i buckets – = 1 (M-n)/M + 2(n/M)(M-n)/M + 3(n/M)2(M-n)/M +. . . • Let = n/M – Time = 1*(1 - ) + 2 (1 - ) + 3 2(1 - ) +. . . – = 1 - + 2 - 2 2 + 3 2 - 3 3 + 4 3 - 4 4. . . – = 1 + + 2 + 3 +. . . = 1/(1 - ) • Assume < 1 – Keep bounded by some constant < 1 18

Rehashing • Hash Table may get full – No more insertions possible • Hash table may get too full – Insertions, deletions, search take longer time • Solution: Rehash – Build another table that is twice as big and has a new hash function – Move all elements from smaller table to bigger table • Cost of Rehashing = O(N) – But happens only when table is close to full – Close to full = table is X percent full, where X is a tunable parameter 19

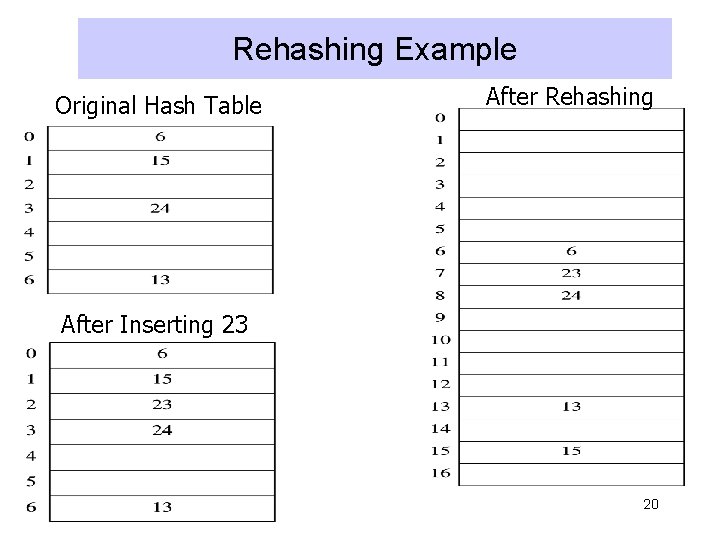
Rehashing Example Original Hash Table After Rehashing After Inserting 23 20

Rehashing Implementation 21

Rehashing implementation 22