Designing Floating Codes for Expected Performance Hilary Finucane

Designing Floating Codes for Expected Performance Hilary Finucane Zhenming Liu Michael Mitzenmacher

Floating Codes • A new model for flash memory. • State is an n-ary sequence of q-ary numbers. – Represents block of n cells; each cell holds an electric charge. • State mapped to variable values. – Gives k-ary sequence of l-ary numbers. • State changes by increasing one or more cell values, or reset entire block. – Adding charge is easy; removing charge requires resetting everything. – Resets are expensive!!!!

Floating Codes: The Problem • As variable values change, need state to track variables. • How do we choose the mapping function from states to variables AND the transition function from variable changes to state changes to maximize the time between reset operations?

History • Write-once memories (WOMs) – Rivest and Shamir, early 1980’s. – Punch cards, optimal disks. – Can turn 0’s to 1’s, but not back again. • Many related models: WOMs, WAMs, WEMs, WUMs. • Floating codes (Jiang, Bohossian, Bruck) use model for Flash Memory. – Designed to maximize worst-case time between resets.

Contribution : Expected Time • Argument: Worst-case time between resets is not right design criterion. – Many resets in a lifetime. – Mass-produced product. – Potential to model user behavior. • Statistical performance guarantees more appropriate. – Expected time between resets. – Time with high probability. – Given a model.

Specific Contributions • Problem definition / model • Codes for simple cases

Formal Model • General Codes • We consider limited variation; one variable changes per step.

Formal Model Continued • Above : when – Cost is 0 when R moves to cell state above previous, 1 otherwise. • Assumption : variables changes given by Markov chain. – Example : ith bit changes with prob. pi – Given D, R, gives Markov chain on cell states. – Let be equilibrium on cell states. • Goal is to minimize average cost: – Same as maximize average time between resets.

Variations • Many possible variations – – Multiple variables change per step More general random processes for values Rules limiting transitions General costs, optimizations • Hardness results? – Conjecture some variations NP-hard or worse.

Specific Case • Binary values : l = 2 • 2 bits : k = 2 • Markov model: only bit changes at each step. First bit changes with probability p. • Result : Asympotically optimal code. – Code handles n(q-1)-o(nq) value changes with high probability. – Same code works for every value of p.

Code : n = 2, k = 2, l = 2 • 2 bit values. • 2 cells. • Code based on striped Gray code. • Expected time/time with high probability before reset = 2 q - o(q) • Asymptotically optimal for all p, 0 < p < 1. • Worst case optimal: approx 3 q/2. D(0, 0) = 00 D(1, 3) = 11 R((1, 0), 2, 1) = (2, 0)

Proof Sketch • “Even cells”: down with probability p, right with probability 1 -p. • “Odd cells” : right with probability p, down with probability 1 -p. • Code hugs the diagonal. • Right/down moves approximately balance for first 2 q-o(q) steps.

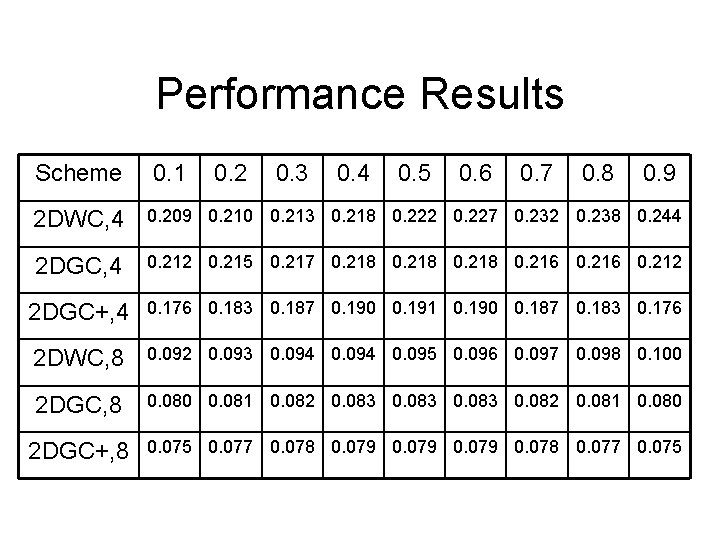
Performance Results Scheme 0. 1 0. 2 0. 3 0. 4 0. 5 0. 6 0. 7 0. 8 0. 9 2 DWC, 4 0. 209 0. 210 0. 213 0. 218 0. 222 0. 227 0. 232 0. 238 0. 244 2 DGC, 4 0. 212 0. 215 0. 217 0. 218 0. 216 0. 212 2 DGC+, 4 0. 176 0. 183 0. 187 0. 190 0. 191 0. 190 0. 187 0. 183 0. 176 2 DWC, 8 0. 092 0. 093 0. 094 0. 095 0. 096 0. 097 0. 098 0. 100 2 DGC, 8 0. 080 0. 081 0. 082 0. 083 0. 082 0. 081 0. 080 2 DGC+, 8 0. 075 0. 077 0. 078 0. 079 0. 078 0. 077 0. 075

Code : n = 3, k = 2, l = 2 • Layer Gray codes for n = 3. • Expected time/time whp before reset = 3 q - o(q) – Slightly hard argument. • Asymptotically optimal for all p, 0 < p < 1.

Codes for k = l = 2 • Glue together codes for larger n. • Example : n = 4. Go 2 q - o(q) in first two dimension, 2 q - o(q) in next two, so 4 q - o(q) overall. • Some further results in paper.

Conclusions • Introduce problem of maximizing expected time until a reset for floating codes. • Simple schemes for k = 2, l = 2 case based on Gray codes. – Building block for larger parameters?

Open Questions • Lots and lots of open questions. – Complexity of finding optimal designs for given parameters. – Asymptotically good codes for larger parameters. – Lower bounds. – Reasonable models for real systems. – Small “families” of codes good over ranges of different user behaviors. – Multi-objective: tradeoffs between average/worstcase performance. – Incorporating error-correction. – Extending to buffer codes, or other models. – And more.