Designing Biasfree Generic Number Guessing Games That Mimic

Designing Bias-free, Generic Number Guessing Games That Mimic the Stock Market and Eliminate Non-randomness Vincent Granville, Ph. D. , Co-founder Data Science Central vincentg@datasciencecentral. com www. Data. Science. Central. com October 20, 2019 CONFIDENTIAL 1

Overview n n Blending number theory, chaos theory, cryptography, HPC, computer science, statistical science, stochastic processes Number guessing game ¨ ¨ ¨ ¨ Public algorithm to compute next winning numbers Design your own ROI table Gains depend on distance between your guess and the winning number Public algorithm requires billions of operations on numbers with 250, 000 digits: not practical Private algorithm kept secret, patent-pending Impossible to reverse engineer (in theory) Blockchain to process financial transactions (victual currency)

Public Algorithm n n Start with initial values x(0) and y(0) that are positive integers, called seeds. Then for t = 0, 1, and so on, compute x(t+1) and y(t+1) iteratively as follows:

Winning Number (I) n 8 -bit system: ¨ ¨ ¨ n n Next winning numbers are always integers between 0 and 255. They occur only at iterations t = T, T + 8, T + 16, T + 24, and so on. Their value at iteration t is x(t) - 256 x(t - 8). The reason for skipping 7 out of 8 numbers is to make sure that winning numbers are not auto-correlated. Past 2, 000 winning numbers are public T > 30, 000 and kept secret even from the operators Seeds x(0), y(0) are public numbers with 250, 000 digits For x(0), see http: //www. datashaping. com/seed 1. txt ¨ For y(0), see http: //www. datashaping. com/seed 2. txt ¨

Winning Number (II) n We guarantee the following: With the wrong seeds, you won't find the winning sub-sequence (matching public past winning numbers) in your lifetime, no matter how much computing power you use. ¨ With the right seeds, you will find the winning sub-sequence (matching public past winning numbers) only once, and in less than 32 trillion iterations ¨ n The algorithm discussed is just an example Linked to the binary digits of 21/2 ¨ 32 -bit and analog systems available too ¨ Private algo is basic: look for 2, 000 past winning numbers in a precomputed sequence of numbers; the next one is next winning number ¨

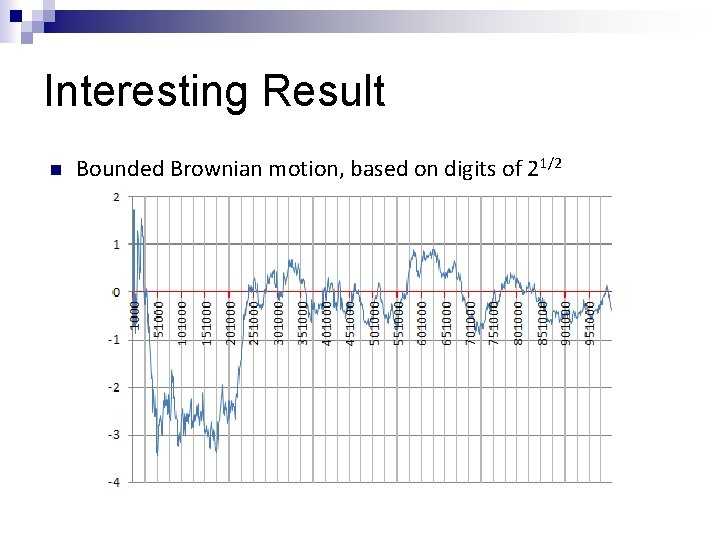
Interesting Result n Bounded Brownian motion, based on digits of 21/2

Unbiased ROI Tables (I) n Definitions and properties (for 8 -bit systems) k = d(x, z) = min(|x - z|, 256 - |x - z|) is the distance between your guess z and the winning number x ¨ G(k) is the multiplier (your $1 bet becomes G(k) dollars) ¨ Unbiased system if ¨ ¨ Variance:

Unbiased ROI Tables (II) n The operator wants An unbiased system (the user pays a fee to participate) ¨ Controlled variance to minimize risks ¨ n Originality Money earned by winners is not based on a re-distribution scheme, unlike lotteries (it’s more like a neutral stock market) ¨ The operator can predict, with a 3 -5% margin of error (depending on the max variance allowed) how much float (gains minus losses) will be left on any given day ¨ Participants can build they own unbiased G(k) function (also called ROI table) that they feel comfortable with, within variance constraints set by the operator or its partners ¨

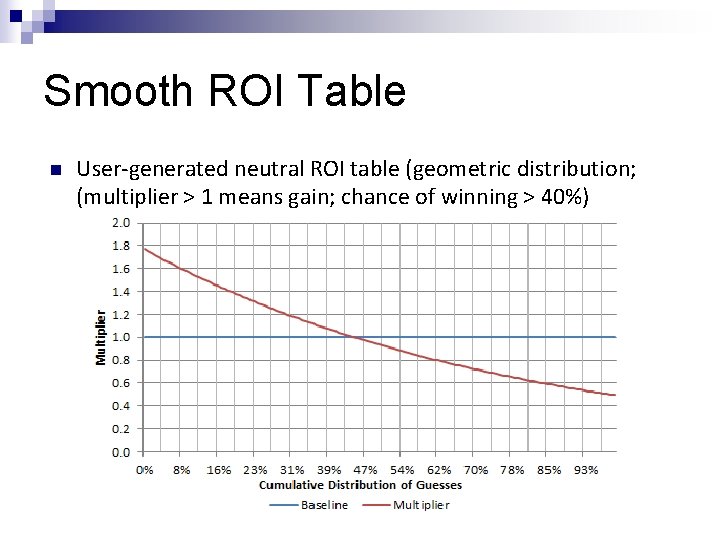
Smooth ROI Table n User-generated neutral ROI table (geometric distribution; (multiplier > 1 means gain; chance of winning > 40%)

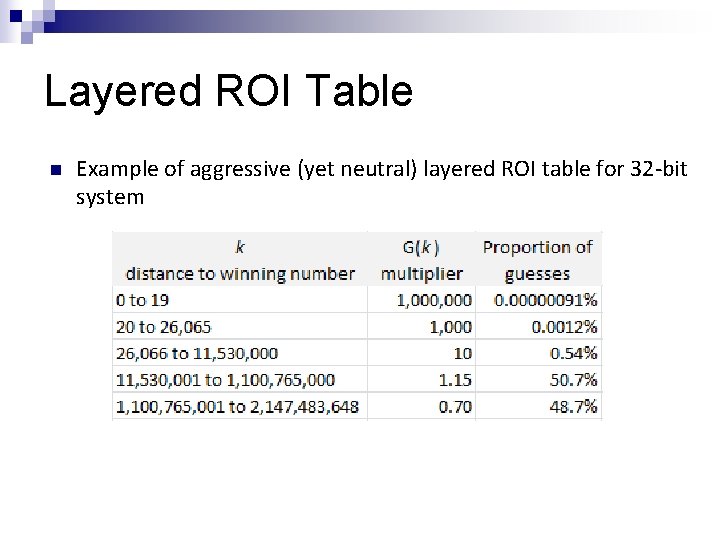
Layered ROI Table n Example of aggressive (yet neutral) layered ROI table for 32 -bit system

Analog System (I) n n The winning number has infinitely many digits. x(t + 1) = { 2 x(t) } where the brackets represent the fractional part function; x(0) = log 2 – log 3. Geometric ROI table: G(k) = p / qk, with p, q > 1, and k (distance to winning number) is now a real number in [0, 1] Properties ¨ ¨ ¨ The maximum multiplier is p The minimum multiplier is p / q The system is fair (un-biased) if p (q - 1) = q log q If the system is fair, the probability of winning is (q - 1) / (q log 2 q) d(x, z) = min(|x - z|, 1 - |x - z|)

Analog System (II) n Implementation details ¨ n x(t) = A(t) log 3 + B(t) log 2 + C(t) where A(t), B(t), and C(t) are integers. Public information The formula x(t + 1) = { 2 x(t) } ¨ Last 2, 000 winning numbers x(T - 1), . . . , x(T - 2000), computed with 20 correct digits ¨ Exact values of A(t), B(t) and C(t) for some secret t between 0 and T ¨ The two constants log 3 and log 2. ¨ n n High precision computing (exact arithmetic) is essential! Need to decorrelate the sequence x(t).

References 1. 2. 3. 4. 5. New Stock Trading and Lottery Game Rooted in Deep Math: https: //dsc. news/2 Ujw 56 b Fascinating New Results in the Theory of Randomness: https: //dsc. news/2 HLUj. TO Two New Deep Conjectures in Probabilistic Number Theory: https: //dsc. news/2 m 0 e. Ued Statistics: New Foundations, Toolbox, and Machine Learning Recipes (300 pages): https: //dsc. news/2 IBy. Rkm Applied Stochastic Processes, Chaos Modeling, and Probabilistic Properties of Numeration Systems (100 pages): https: //dsc. news/2 J 80 pjl