Designing and Building FileFolder Bridges as an Introduction

Designing and Building File-Folder Bridges as an Introduction to Engineering The Waddell ATruss Bridge COL Stephen Ressler, P. E. , Ph. D. Department of Civil & Mechanical Engineering U. S. Military Academy, West Point

Objectives o Learn about structural engineering: n Through a hands-on bridge-building project. n Through the use of free computer software. o Learn about the ongoing West Point Bridge Design Contest.

Project o Students receive a pile of Popsicle sticks and some glue. o Students build a bridge, based on. . . A picture. n A vague idea of what a bridge should look like. n o Bridges are weighed. o Bridges are tested to failure. o Highest strength-to-weight ratio wins. What do students actually learn from this experience?

What They Don’t Learn The Essential Characteristics Of Engineering o. A systematic design process precedes construction. o Engineers design; Contractors build. o The design process is informed by math and science. o Design is iterative. o Structures are designed to carry code-specified loads safely and economically. n n Designed to stand up, not to fail. Strength-to-weight ratio is never the objective.

Why File Folders? o Inexpensive. o Easy to cut, bend, and glue. o Surprisingly predictable structural behavior. o Can be used to build: Tubes and bars. n Connections that are stronger than the attached structural members. n

Our Agenda o Introduction o Start to Truss Bridges building a truss o Forces and equilibrium o Continue building the truss o Structural o Finish analysis the truss o Materials testing o Structural evaluation o Structural design n n Manual method Using the West Point Bridge Designer This allows time for the glue to dry

What You Need to Know o For n building a file-folder bridge: NONE o For analyzing a file-folder bridge: Basic algebra n Geometry – Pythagorean Theorem n Trigonometry – sine and cosine n Physics – forces, equilibrium n Computers – spreadsheets n o For n the West Point Bridge Designer NONE These concepts could be taught in the context of this project
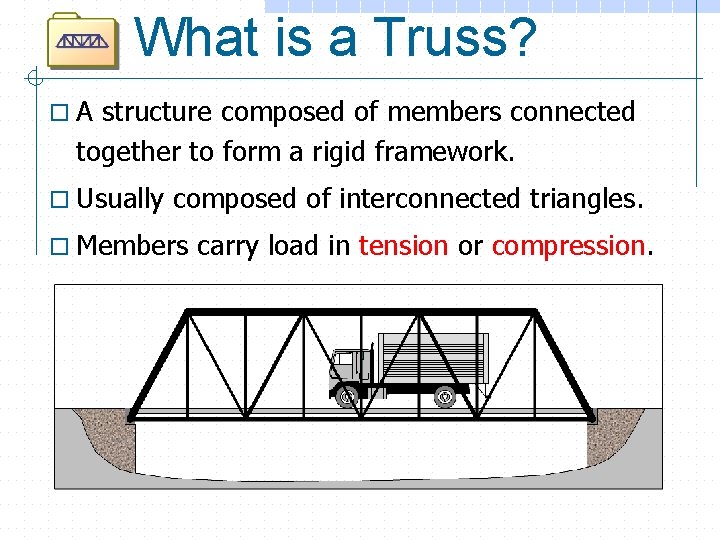
What is a Truss? o. A structure composed of members connected together to form a rigid framework. o Usually composed of interconnected triangles. o Members carry load in tension or compression.
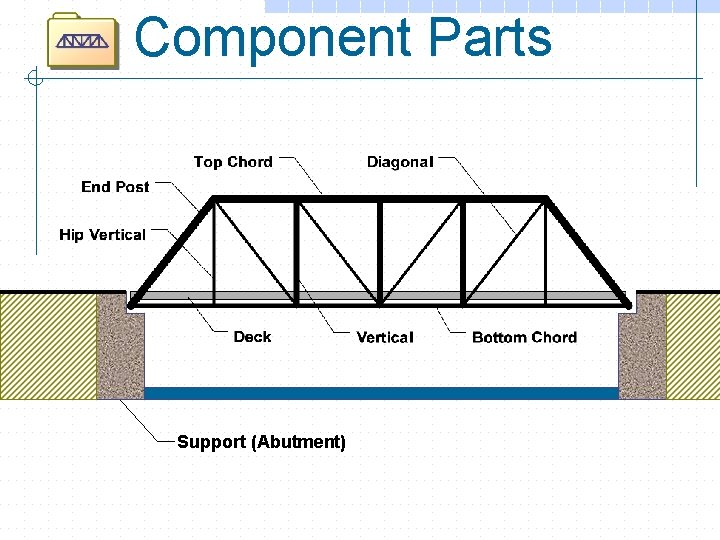
Component Parts Support (Abutment)

Configurations
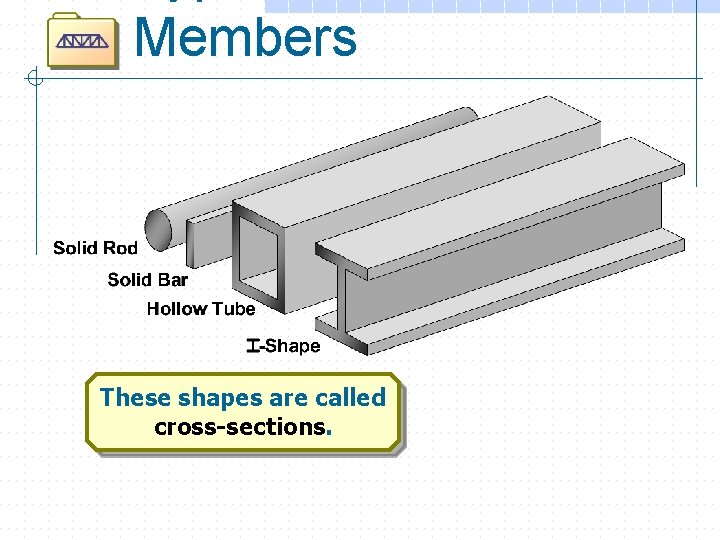
Members These shapes are called cross-sections.
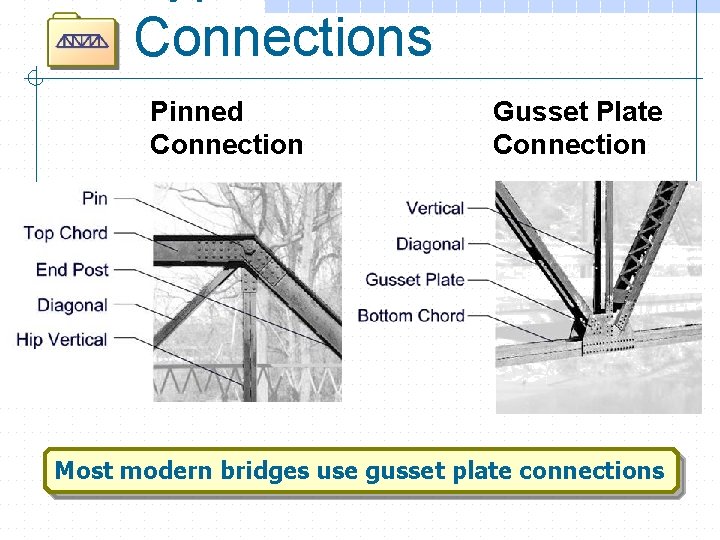
Connections Pinned Connection Gusset Plate Connection Most modern bridges use gusset plate connections

Let’s build this bridge. . . Waddel “A Truss” Bridge over Lin Branch Creek Trimble, MO
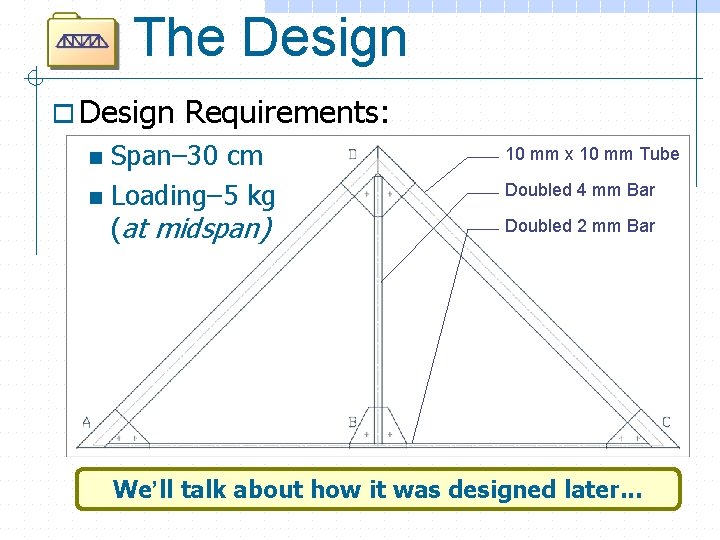
The Design o Design Requirements: Span– 30 cm n Loading– 5 kg (at midspan) n 10 mm x 10 mm Tube Doubled 4 mm Bar Doubled 2 mm Bar We’ll talk about how it was designed later. . .

Our A-Truss Bridge

Materials & Equipment o File folders o Yellow carpenter’s glue o Building board (Styrofoam or cork) o Pins o Scissors o Metal ruler* o Hobby knife or single-edge razor blade* o Rubber cement* *Required only for prefabrication of structural members
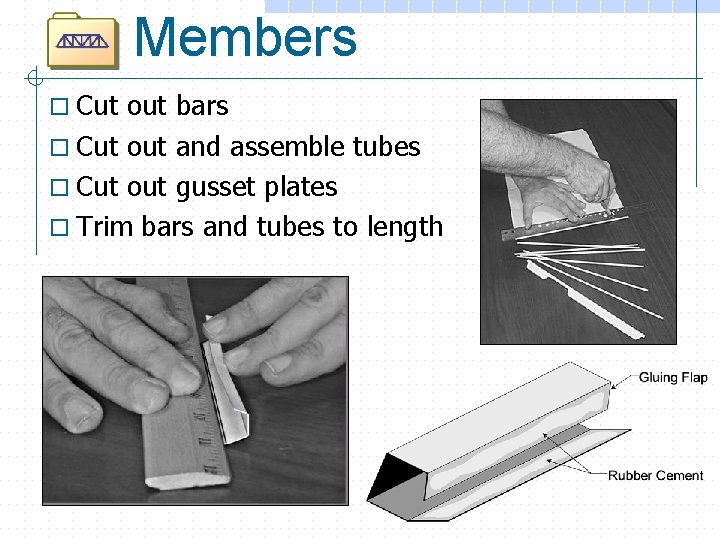
Members o Cut out bars o Cut out and assemble tubes o Cut out gusset plates o Trim bars and tubes to length
to Length Bottom Chords (2 per team)
to Length Bottom Chords (2 per team)
to Length Verticals (2 per team)
to Length Verticals (2 per team)
to Length End Posts (2 per team)
to Length End Posts (2 per team)
Board Each Team Member: o Place the layout drawing on your building board.
Board o Place a sheet of plastic wrap over the layout drawing.
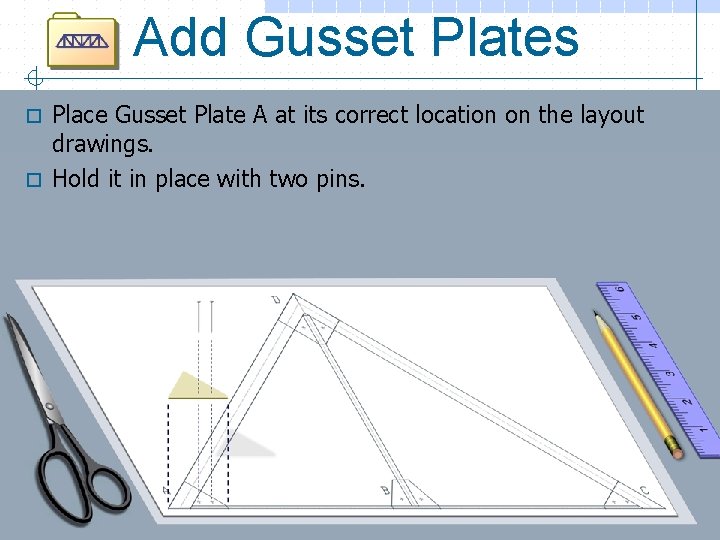
Add Gusset Plates Place Gusset Plate A at its correct location on the layout drawings. o Hold it in place with two pins. o
Add Gusset Plates o Repeat the process for Gusset Plates B, C, and D.
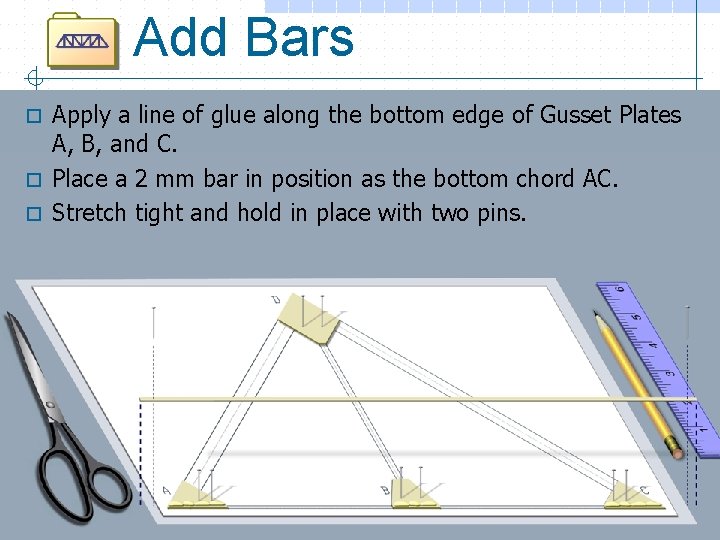
Add Bars Apply a line of glue along the bottom edge of Gusset Plates A, B, and C. o Place a 2 mm bar in position as the bottom chord AC. o Stretch tight and hold in place with two pins. o
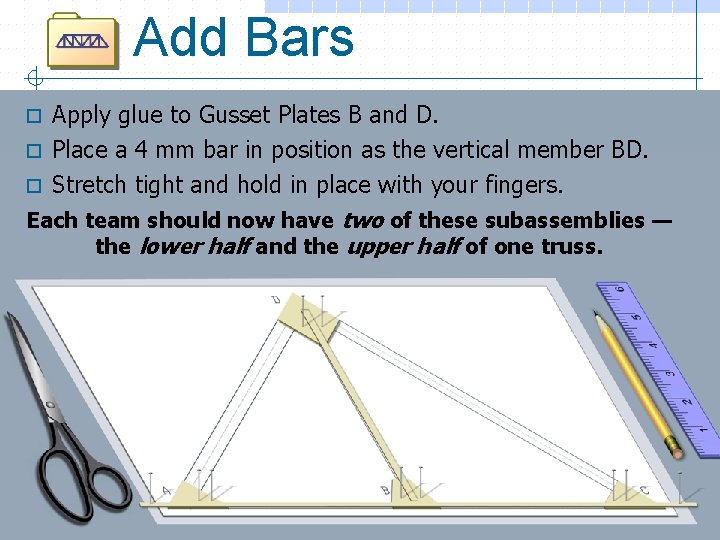
Add Bars Apply glue to Gusset Plates B and D. o Place a 4 mm bar in position as the vertical member BD. o Stretch tight and hold in place with your fingers. Each team should now have two of these subassemblies — the lower half and the upper half of one truss. o
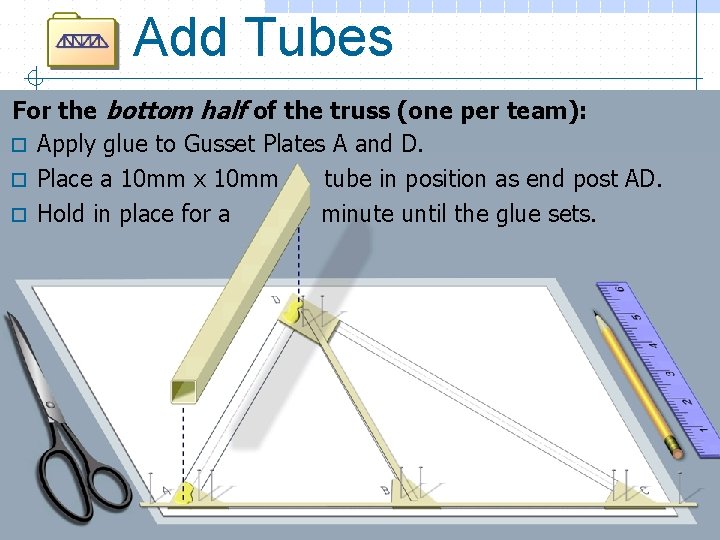
Add Tubes For the bottom half of the truss (one per team): o Apply glue to Gusset Plates A and D. o Place a 10 mm x 10 mm tube in position as end post AD. o Hold in place for a minute until the glue sets.

Add Tubes Apply glue to Gusset Plates C and D. o Place a 10 mm x 10 mm tube in position as end post AD. o Hold in place for a minute until the glue sets. o
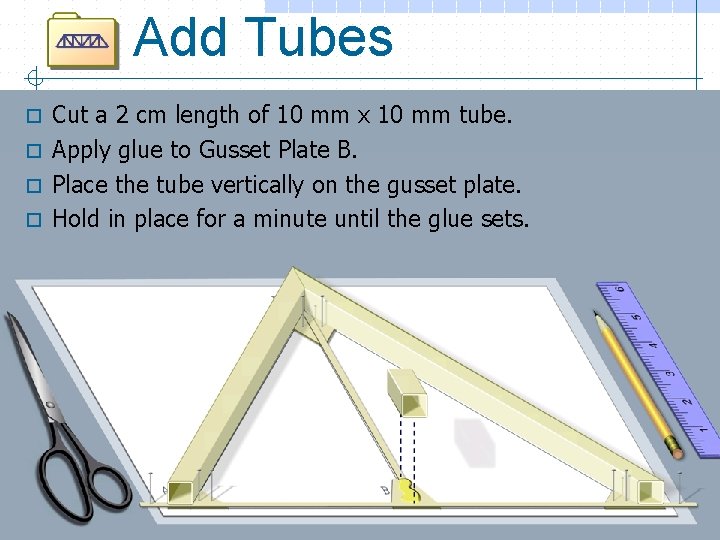
Add Tubes Cut a 2 cm length of 10 mm x 10 mm tube. o Apply glue to Gusset Plate B. o Place the tube vertically on the gusset plate. o Hold in place for a minute until the glue sets. o
Truss o Allow all glue joints to dry.

Reactions o Force – A push or pull. o Load – A force applied to a structure. Self-weight of structure, weight of vehicles, pedestrians, snow, wind, etc. o Reaction – A force developed at the support of a structure to keep that structure in equilibrium. Forces are represented mathematically as VECTORS.

Equilibrium Newton’s First Law: An object at rest will remain at rest, provided it is not acted upon by an unbalanced force. A Load. . . and Reactions

Compression An unloaded member experiences no deformation Tension causes a member to get longer Compression causes a member to shorten
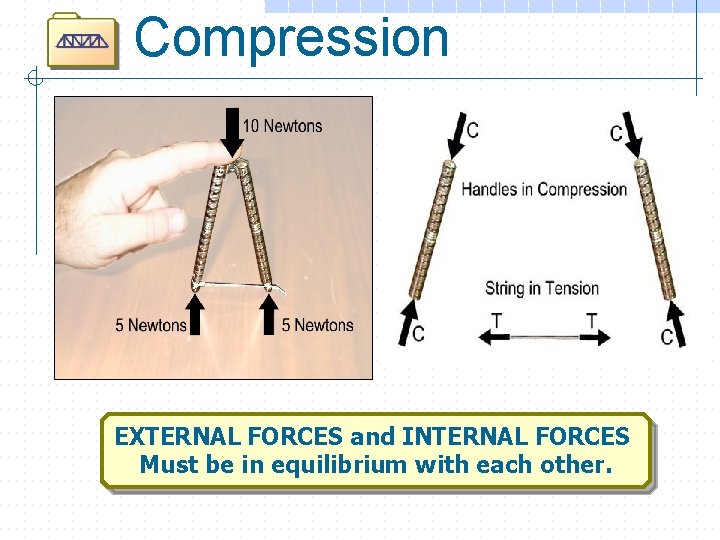
Compression EXTERNAL FORCES and INTERNAL FORCES Must be in equilibrium with each other.
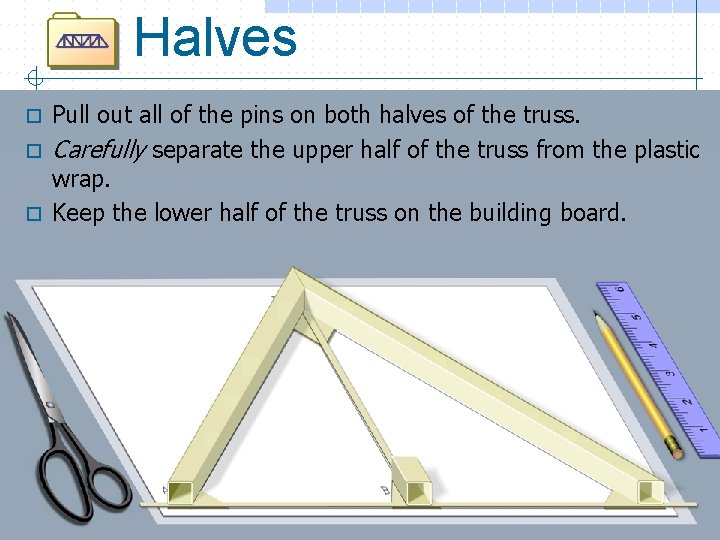
Halves Pull out all of the pins on both halves of the truss. o Carefully separate the upper half of the truss from the plastic wrap. o Keep the lower half of the truss on the building board. o
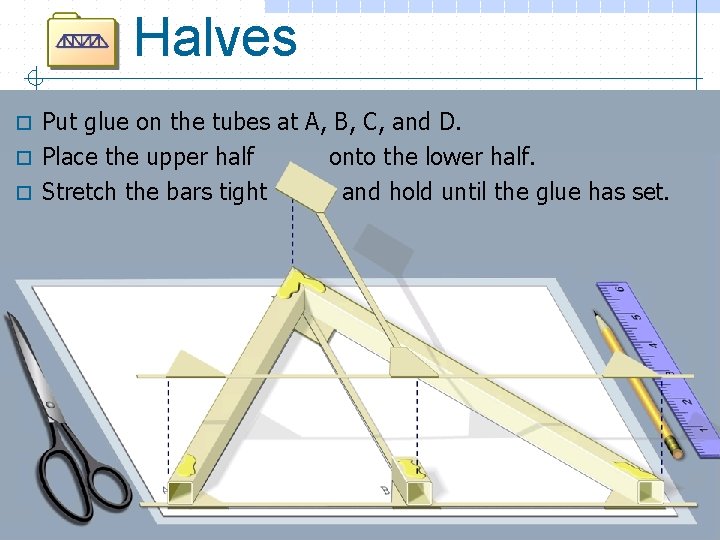
Halves Put glue on the tubes at A, B, C, and D. o Place the upper half onto the lower half. o Stretch the bars tight and hold until the glue has set. o

Halves o Allow all glue joints on the completed truss to dry.

Structural Analysis o For a given load, find the internal forces (tension and compression) in all members. o Why? o Procedure: n Model the structure: w Define supports w Define loads w Draw a free body diagram. Calculate reactions. n Calculate internal forces using “Method of Joints. ” n
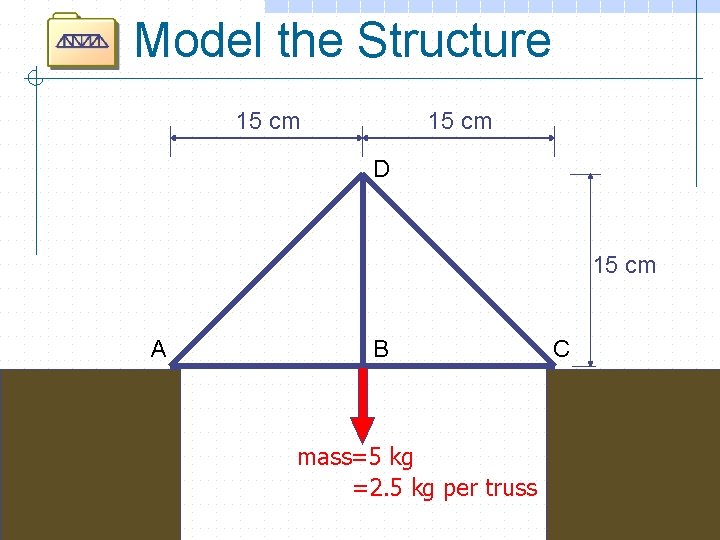
Model the Structure 15 cm D 15 cm A B mass=5 kg =2. 5 kg per truss C
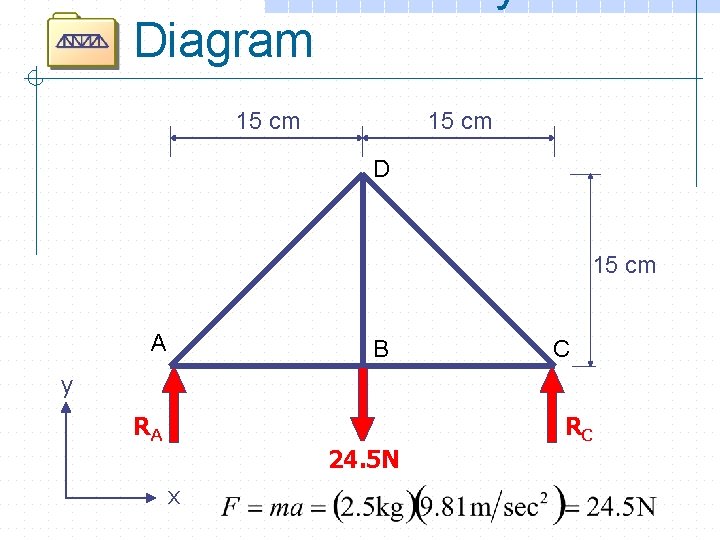
Diagram 15 cm D 15 cm A B C y RA mass=2. 5 24. 5 N kg x RC
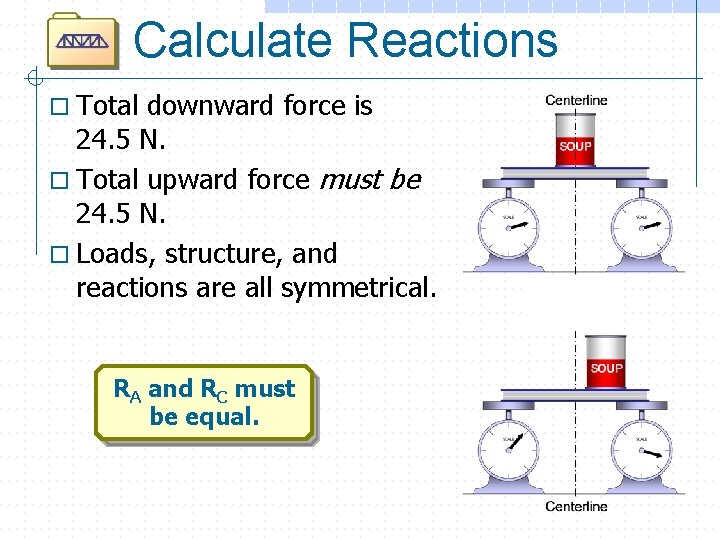
Calculate Reactions o Total downward force is 24. 5 N. o Total upward force must be 24. 5 N. o Loads, structure, and reactions are all symmetrical. RA and RC must be equal.
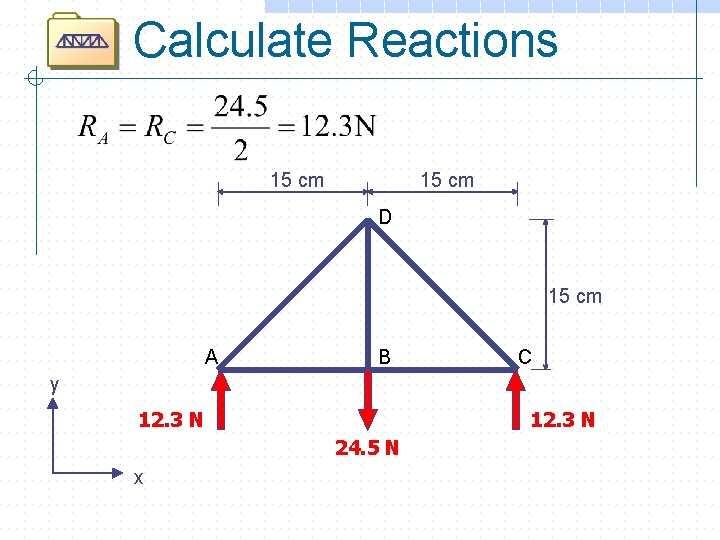
Calculate Reactions 15 cm D 15 cm A B C y 12. 3 RNA x 24. 5 N 12. 3 N R C
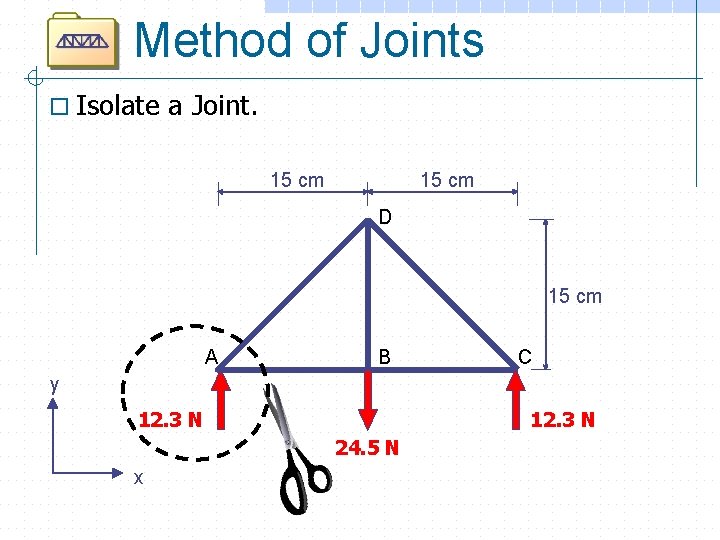
Method of Joints o Isolate a Joint. 15 cm D 15 cm A B C y 12. 3 N 24. 5 N x 12. 3 N R C

Method of Joints o Isolate a Joint. o Draw a free body diagram of the joint. n n n FAD y A FAB 12. 3 N Include any external loads of reactions applied at the joint. x Include unknown internal forces at every point where a member was cut. Assume unknown forces in tension. o Solve the Equations of Equilibrium for the Joint. EXTERNAL FORCES and INTERNAL FORCES Must be in equilibrium with each other.

Equations of Equilibrium o The sum of all forces acting in the x-direction must equal zero. FAD A y FAB 12. 3 N o The sum of all forces acting in the y-direction must equal zero. o For x forces that act in a diagonal direction, we must consider both the x-component and the y -component of the force.

Components of Force y (FAD)y FAD q A x q A (FAD)x o If magnitude of FAD is represented as the hypotenuse of a right triangle. . . o Then the magnitudes of (FAD)x and (FAD)y are represented by the lengths of the sides.
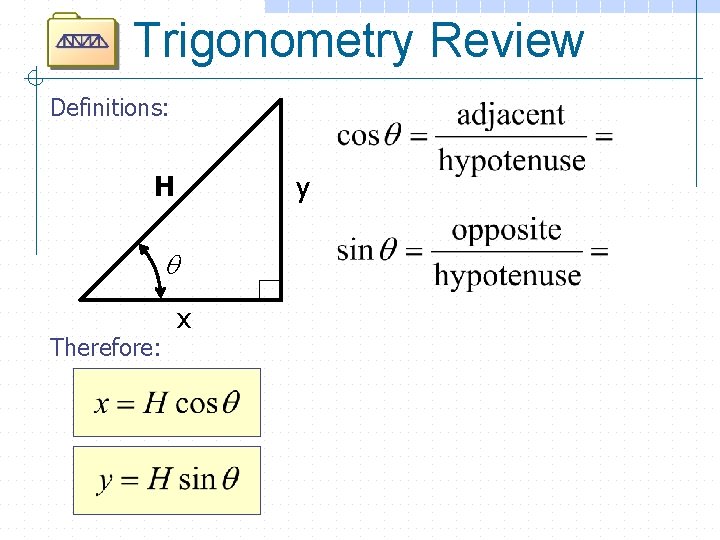
Trigonometry Review Definitions: H y q Therefore: x

Components of Force y (FAD)y FAD q= 45? o A Therefore: x q= 45? o A (FAD)x

Equations of Equilibrium 0. 707 FAD A y FAB 12. 3 N ? x FAB=12. 3 N (tension) FAD=17. 3 N (compression)
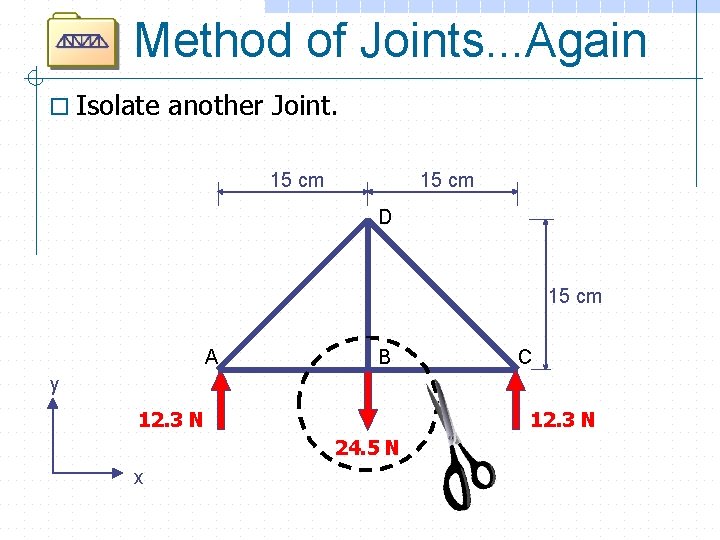
Method of Joints. . . Again o Isolate another Joint. 15 cm D 15 cm A B C y 12. 3 N 24. 5 N x 12. 3 N R C

Equations of Equilibrium FBD FAB FBC=12. 3 N (tension) B y 24. 5 N x FBD=24. 5 N (tension) FBC
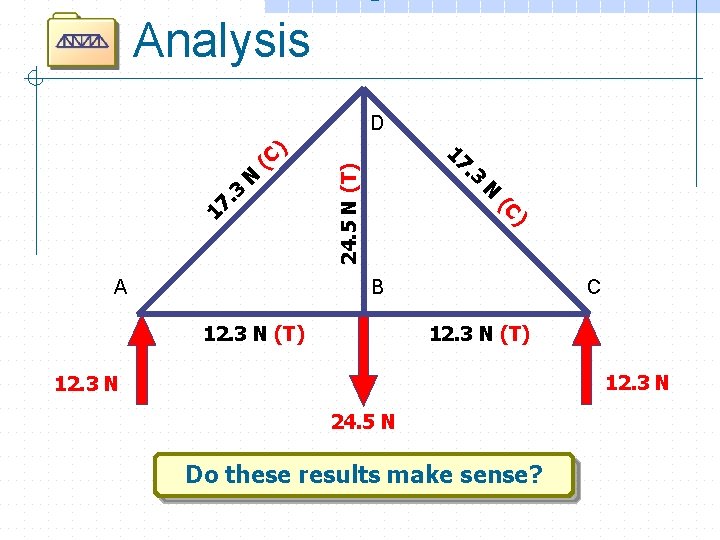
Analysis N 24. 5 N (T) N ) (C 17. 3 3 A . 17 (C ) D B 12. 3 N (T) C 12. 3 N (T) 12. 3 N 24. 5 N Do these results make sense?
Finish the Truss o Trim off the excess length on both bottom chords (AC).
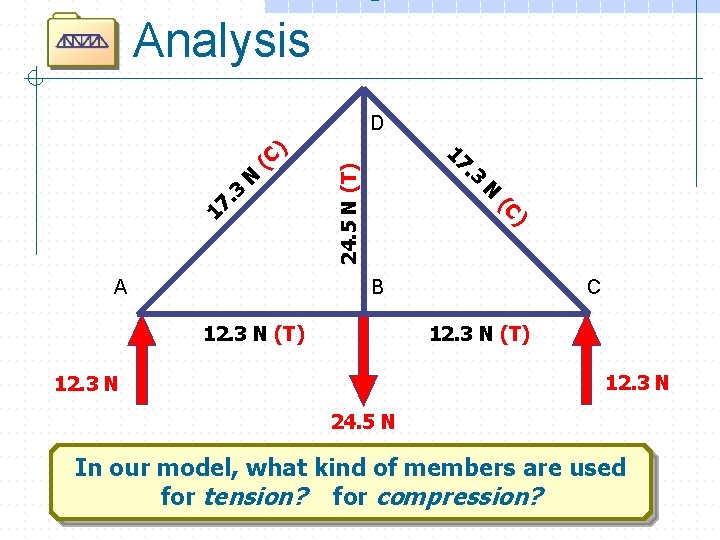
Analysis N 24. 5 N (T) N ) (C 17. 3 3 A . 17 (C ) D B 12. 3 N (T) C 12. 3 N (T) 12. 3 N 24. 5 N In our model, what kind of members are used for tension? for compression?

Materials Testing – The largest internal force a structural member can experience before it fails. o Failure – The condition that occurs when the internal force exceeds the strength of a member o Strength TENSILE STRENGTH ≠ COMPRESSIVE STRENGTH

Machine
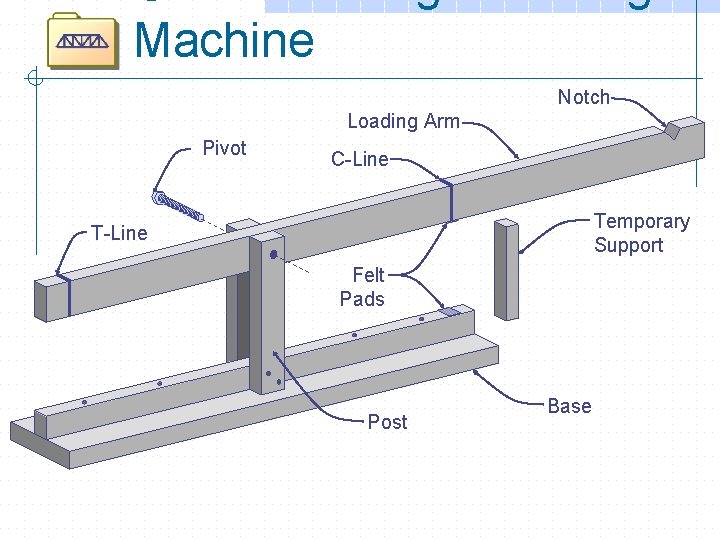
Machine Notch Loading Arm Pivot C-Line Temporary Support T-Line Felt Pads Post Base

Testing Tensile Strength The test setup.
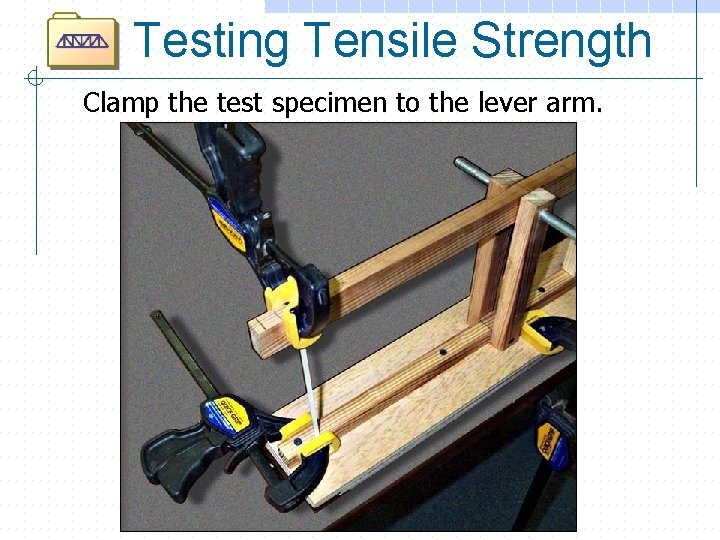
Testing Tensile Strength Clamp the test specimen to the lever arm.

Testing Tensile Strength Slowly add sand to the bucket.

Testing Tensile Strength When the specimen breaks, weigh the bucket and compute the tensile strength.
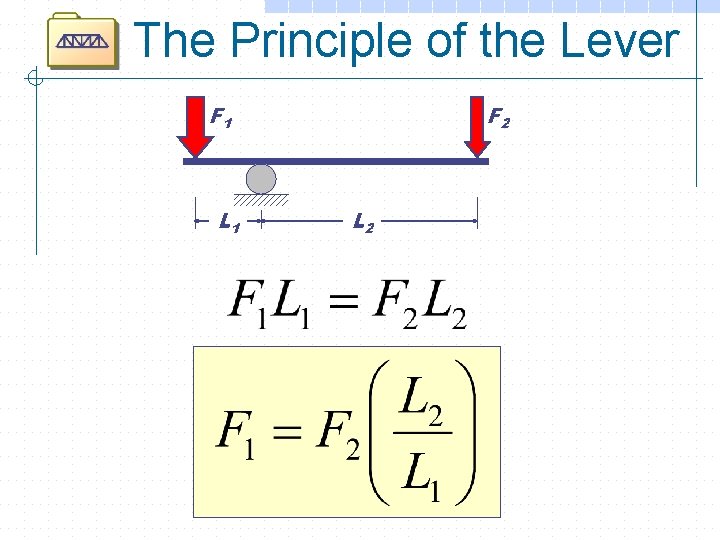
The Principle of the Lever F 1 L 1 F 2 L 2

Testing o Tensile strength depends on: Type of material n Thickness of cross-section n Width of cross-section n o Tensile strength does not depends on: Length of member n Shape of cross-section n
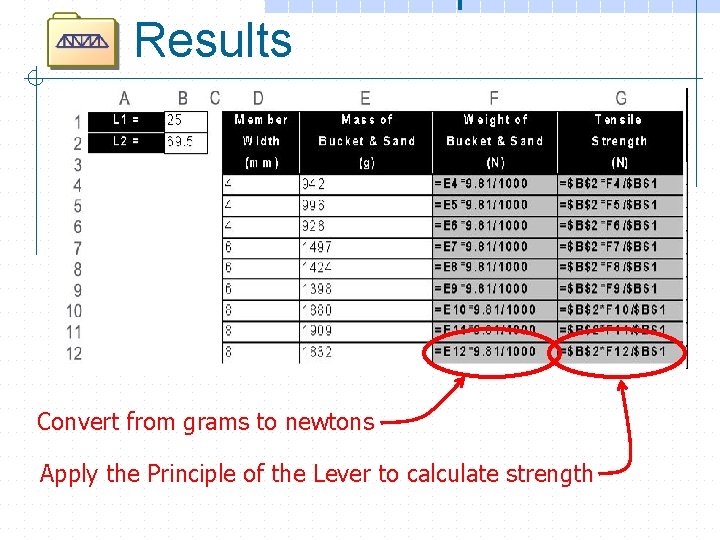
Results Convert from grams to newtons Apply the Principle of the Lever to calculate strength
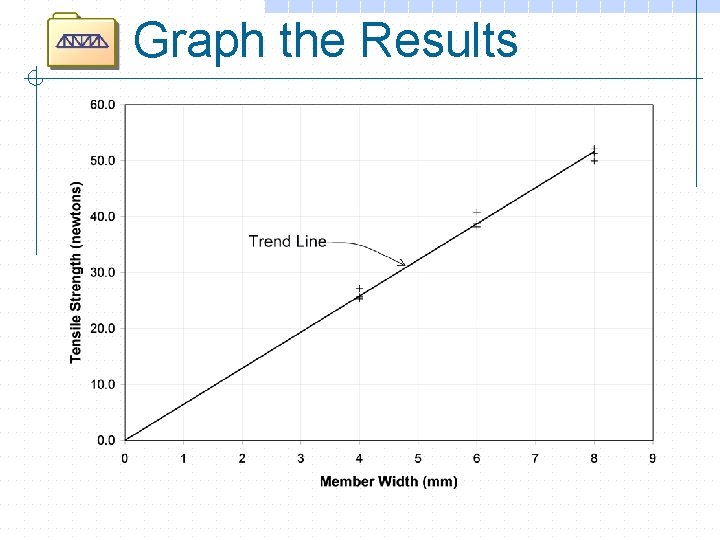
Graph the Results

Strength The test setup.

Strength A compression specimen at failure.
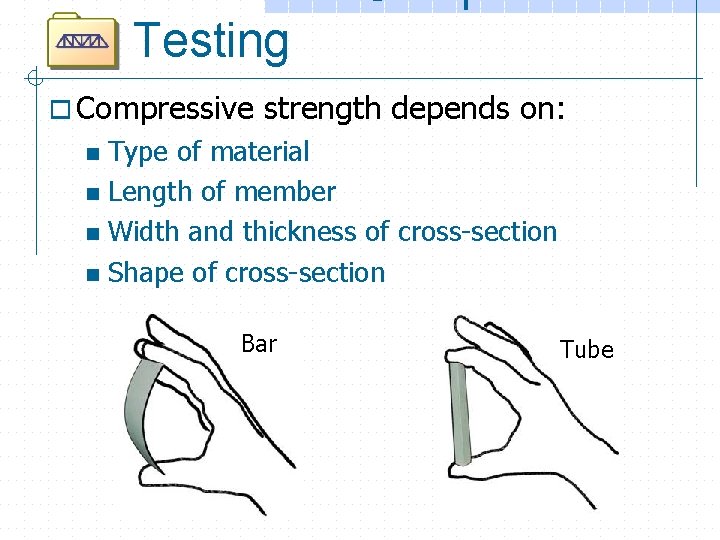
Testing o Compressive strength depends on: Type of material n Length of member n Width and thickness of cross-section n Shape of cross-section n Bar Tube
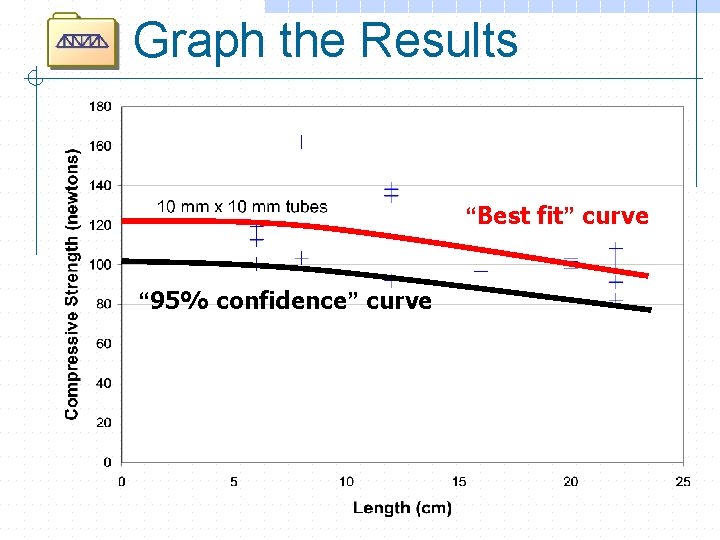
Graph the Results “Best fit” curve “ 95% confidence” curve

Structural Evaluation o Is the internal member force less than the strength for each member? o Calculate the Factor of Safety:
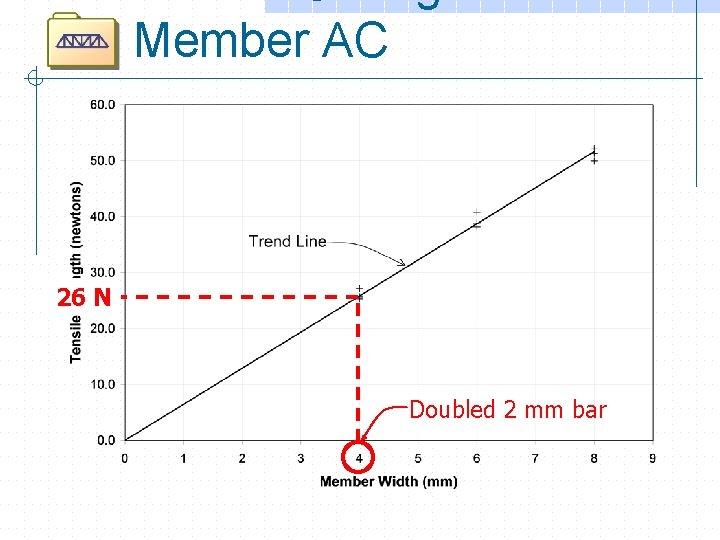
Member AC 26 N Doubled 2 mm bar

Member AC >1 SAFE! Structures are normally designed for a FS of at least 1. 6.
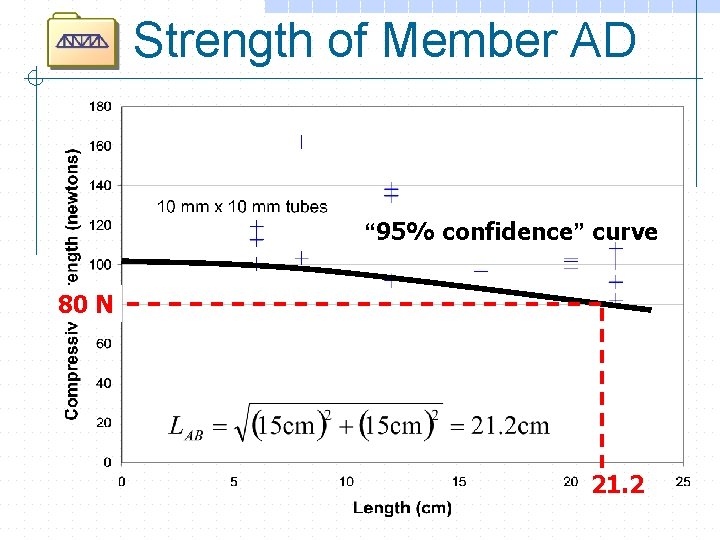
Strength of Member AD “ 95% confidence” curve 80 N 21. 2

Factor of Safety for AD > 1 VERY SAFE! Are the end posts excessively strong?

Service The completed bridge Load test with 5 kg of sand suspended from midspan

Structural Design o Design n Requirements: Span, loading, factor of safety o Decide on truss configuration. o Perform a structural analysis. n n Reactions Internal member forces o Select member sizes based on required strength. o Draw plans. Please don’t o Build the bridge. break o Test – Can the bridge carry the bridge! the required loading safely?

Designer o Look and feel of a standard CAD package. o Easy to create a successful design. o Hard to create a highly competitive design. o Highly successful: n n n Over 150, 000 copies downloaded since 2000. Two major national software awards. Formally endorsed as an educational tool by the American Society of Civil Engineers. o Runs on Windows 95 (or later) PC.
Design Contest o Started on January 8, 2004. o Students age 13 through grade 12 are eligible for prizes. o To enter: n Use the West Point Bridge Designer 2004 to design a bridge. n Upload the design to our website for automated judging. n Receive instant feedback about contest standing. o $15, 000 scholarships for the winners. o Participation is free!

Summary o File-folder n n n Accurate representation of real bridges Vehicle for learning engineering concepts. Design based on authentic applications of math, science, and computer technology. o The n n West Point Bridge Designer: Experience the engineering design process. Free! o The n bridges: West Point Bridge Design Contest: Please help us make it successful!
- Slides: 82