Design versus Programming in Custom Computing Experiences using

Design versus Programming in Custom Computing: Experiences using the ASM Method James P. Davis, Ph. D. Heather Wake Conor Leehaug Nirish Namilae University of South Carolina Department of Computer Science and Engineering MAPLD-04 Davis, Wake, Leehaug & Namilae 1 227 -MAPLD 04

Outline • Process – Custom Computing for Mobile Computing – Algorithm to Architecture – Language-based versus Model-based formulation • Method – Algorithmic State Machine (ASM) • Examples – Reed-Solomon coding for wireless networks. • Lessons Learned Davis, Wake, Leehaug & Namilae 2 227 -MAPLD 04

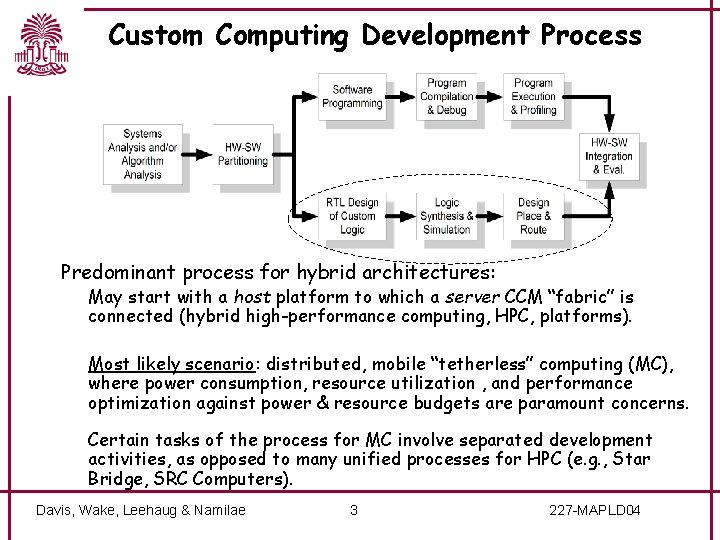
Custom Computing Development Process Predominant process for hybrid architectures: May start with a host platform to which a server CCM “fabric” is connected (hybrid high-performance computing, HPC, platforms). Most likely scenario: distributed, mobile “tetherless” computing (MC), where power consumption, resource utilization , and performance optimization against power & resource budgets are paramount concerns. Certain tasks of the process for MC involve separated development activities, as opposed to many unified processes for HPC (e. g. , Star Bridge, SRC Computers). Davis, Wake, Leehaug & Namilae 3 227 -MAPLD 04

Paths from Algorithm to Architecture Language-driven approach: Use programming language as medium for algorithm expression. Goal: hide the details of the platform from the programmer. Rely on technology embodied in tools: (1) programming idioms; (2) compiler technology; (3) abstraction libraries. Model-driven approach: Use explicit modeling language, providing algorithm constructs, and “cues” for constructing viable architectures. Goal: allow designer to use analogical reasoning, planning, & configuration skills to propose and refine solutions in space. Davis, Wake, Leehaug & Namilae 4 227 -MAPLD 04

Graphical Modeling versus Programming • Human mind works more effectively with visual and spatial information. – Learning, retention, manipulation of artifacts, & communicating ideas. – During human evolution, we spent more time using pictures to convey ideas rather than text writing (e. g. , petroglyphs at Lascaux, France). – We use graphical representation of design artifacts annotated with textual components. • Graphical notations more effective in “chunking” design information. – A few changes in graphical model imply larger number of changes in code. – More compact representation in graphics. – The “links” between constructs carry much information. • Design consists of planning and configuration tasks, which are easier to perform with diagrammatic representations than textual ones. • Graphics allows designers to keep focus on artifacts of architecture. – Analogical focus makes possible better trade-offs – Allows more “agile” exploration of design space. Davis, Wake, Leehaug & Namilae 5 227 -MAPLD 04

Algorithm to Architecture Description-1 • Sources for transforming to architecture model: – May start with mathematical formulation (e. g. , GF(2 m)). – May start with algorithm & abstract data type formulation. – May start with existing architecture pattern (e. g. , LFSR). Davis, Wake, Leehaug & Namilae 6 227 -MAPLD 04

Algorithm to Architecture Description-2 Davis, Wake, Leehaug & Namilae • Algorithm Specification: • Platform Independent Model: • Platform Specific Model: • Bounding the search space: – Describe problem solving in algorithm steps and abstract data type (ADT). – Mapping algorithm and ADT onto initial architecture choice. – Use behavioral & architectural patterns: (1) polling, (2) handshaking, (3) arbitration, (4) rendezvous, (5) pipelining, (6) iteration & repetition (systolic). – Explore architecture space: serial to increasingly parallel. – Refine PIM onto target platform to create PSM. – Account for device resources, number of devices, device interconnect. – Use of estimators (cf. , Quan et al. , 2004). – Characterize key points on architecture continuum, converge to “satisficing” point. 7 227 -MAPLD 04

Algorithmic State Machine Method-1 • Using Algorithmic State Machine Method – We use Executable ASM diagrams to model state machine behavior and datapath operations for the hardware. – Executable ASM models have graphical symbol set that looks like a flowchart. – Algorithm structure can be easily modeled using the ASM graphics. – The diagrams are annotated with register transfer notation (RTN) expressions for operations and events. – ASM models are executed in Nimbus. TM, are compiled into simulation model, then translated into VHDL code for circuit synthesis. Davis, Wake, Leehaug & Namilae 8 227 -MAPLD 04

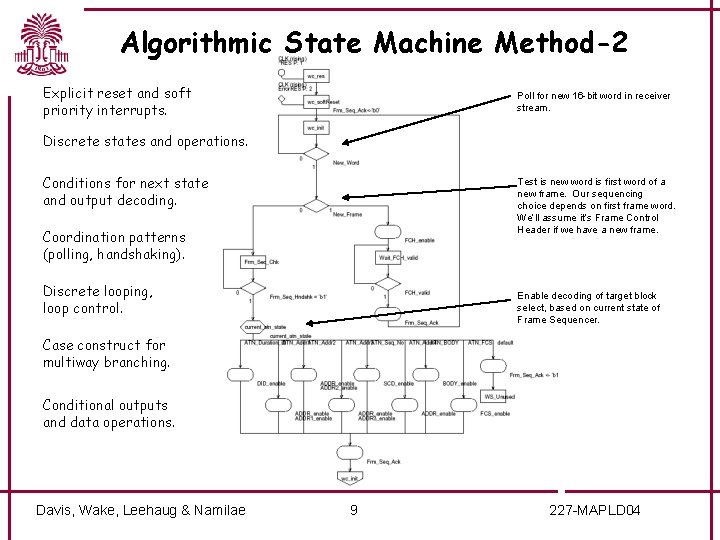
Algorithmic State Machine Method-2 Explicit reset and soft priority interrupts. Poll for new 16 -bit word in receiver stream. Discrete states and operations. Conditions for next state and output decoding. Test is new word is first word of a new frame. Our sequencing choice depends on first frame word. We’ll assume it’s Frame Control Header if we have a new frame. Coordination patterns (polling, handshaking). Discrete looping, loop control. Enable decoding of target block select, based on current state of Frame Sequencer. Case construct for multiway branching. Conditional outputs and data operations. Davis, Wake, Leehaug & Namilae 9 227 -MAPLD 04

Reed-Solomon R-S(n, k) Model • Background – Wireless communications in noisy environments can consume much bandwidth on frame retransmission after timeout. – What if we could not just detect errors, but correct certain error bursts, at speed? – We are interested in alternate error coding and correction schemes to evaluate tradeoffs in code strength, codeword overhead, channel error rate, and channel capacity. – We use IEEE 802. 11 b protocol as experimental platform: (1) construct circuit models for MAC/PHY layers, (2) collect station timing data from logic model, (3) correlate against network model in ns-2 simulator. – Replace CRC-32 with R-S(n, k) in 802. 11 b MAC Layer? Davis, Wake, Leehaug & Namilae 10 227 -MAPLD 04

Reed-Solomon R-S(n, k) Model • Structure – We have a symbol stream into which we want to append coding bits to form a “codeword”. – m-bit dataword sequence, with k data words encoded to form n codewords with 2 t parity words appended. – The symbol error correcting capability of the code is up to t words. • Mathematics – The construction of a code is done within a “finite field” that is closed under addition and multiplication. – Non-binary cyclic coding has better performance than binary, so we require a field extension over a GF(2 m) field when m isn’t a prime, but is a power of a prime (2 m). – We characterize the field, and its coding patterns, according to polynomial expressions. – We carry out finite field arithmetic (addition, multiplication) on a complete symbol. Generator polynomial for R-S(7, 3): g(X) = a 3 + a 1 X + a 0 X 2 + a 3 X 3 + X 4 Davis, Wake, Leehaug & Namilae 11 227 -MAPLD 04

R-S(7, 3) – Codeword Generation • Linear Feedback Shift Register (LFSR) – Means of formulating GF(23) polynomial code generator circuit. – Shift Register, (n-k) stages: k clock cycles to shift in m-bit input message words. – Input message words simultaneously moved to LFSR and output register Reg 4 (uncoded data portion of codeword). – LFSR, modulo arithmetic performed on message words to generate parity words. – Remainder of (n-k) cycles shift out the parity words appended to form complete codeword for transmission. Generator polynomial for R-S(7, 3): g(X) = a 3 + a 1 X + a 0 X 2 + a 3 X 3 + X 4 Source: Sklar, © 2001, Prentice-Hall Publishers, Inc. Davis, Wake, Leehaug & Namilae 12 227 -MAPLD 04

R-S(7, 3) – Syndrome Computation-1 • First pass modeling: – Define logical array to store received codeword, and obtain each symbol from the received bitstream in parallel (using a register file). – Syndrome values computed as result of parity check on the received computed codeword polynomial: r(X) = U(X) + e(X). r(X) = a 0 + a 2 X + a 4 X 2 + a 0 X 3 + a 6 X 4 + a 3 X 5 + a 5 X 6 – We run computation for MUL, then ADD, in order to check r(X) = 0 at each root of generator g(X) polynomial to see we have valid codeword. – Enable the MULs and ADDs for syndrome equations as register-based table lookups, in parallel for each syndrome symbol. – Broadcast active low ‘go_mul’ and ‘go_add’ signals to all concurrent ASM threads. Davis, Wake, Leehaug & Namilae 13 227 -MAPLD 04

R-S(7, 3) – Syndrome Computation-2 • Multiplication thread structure: – On enable, ASM thread uses a Case selection for coefficient lookup. – For small R-S(7, 3) code, this is likely most efficient. – For larger codewords, such as R-S(63, 59) or RS(255, 247), use of modulo arithmetic unit may be required to increase throughput. Davis, Wake, Leehaug & Namilae 14 227 -MAPLD 04

R-S(7, 3) – Syndrome Computation-3 • Addition thread structure: – Outer control loop for iterating on the S-alpha terms. – Lookup of S-alpha (q) to form offset for addition table (addbits). – Assignment for higher coefficients is mod(m), as multiple Case paths make the same assignment. – Check at the end of thread for syndrome = 0. – Logic for Error localization not shown. – Syndrome ADD logic debugged, then replicated into multiple, concurrent threads to increase parallelism. Davis, Wake, Leehaug & Namilae 15 227 -MAPLD 04

R-S(n, k) Modular Multiplication-1 Davis, Wake, Leehaug & Namilae 16 • Montgomery multiplier algorithm breaks logically into three parts: – convert to Montgomery numbers (within closed GF(n) field). – do the multiplication. – convert back to Integer numbers. • Each conversion requires both Multiplication and Modulo operations. – Conversion to/from modulo operators shown in ASM thread. – Actual MUL operations on modular operators abstracted to a sub-flow within scope of ASM thread. 227 -MAPLD 04

R-S(n, k) Modular Multiplication-2 Results of assignments used as inputs for later macro computations. • Montgomery modular MUL steps – Upon conversion into modular operators, carry out the 3 MUL operations. – No opportunity to increase parallelism in these MULs, because of dependencies. – However, we could modify the thread structure so that data path is pipelined. – Instead of having this as sub-flow, make it separate thread, controlled with handshaking signals. Davis, Wake, Leehaug & Namilae 17 227 -MAPLD 04

Sub-Multiplication – Parallel Partials Source: Carpinelli, © 2002 Pearson Publishing, Inc. Davis, Wake, Leehaug & Namilae 18 227 -MAPLD 04

Faster Addition – Multi-operand Trees Adder delay for a Carry Save Adder architecture is much less than other one. CSA has two-stage logic. It takes three operands, putting one on the Carry In and generates two outputs on the Sum and Carry Out. The (3, 2) reduction allows multi-operand addition to be done, which is faster than repeated 2 -operand addition. Here, all 16 partials are added at the same time. Source: Leehaug & Davis, 2004 Davis, Wake, Leehaug & Namilae 19 227 -MAPLD 04

ASM Model of 16 x 16 Wallace Multiplier Davis, Wake, Leehaug & Namilae 20 227 -MAPLD 04

Exploration Process - Methods & Tools Exsedia Nimbus. TM & IPalette. TM Xilinx ISE TM Download Bitstream Davis, Wake, Leehaug & Namilae 21 227 -MAPLD 04

Designer Productivity – Effort Distribution In the modeling exercise, three separate logic circuits of the larger architecture were explored: R-S(n, k) coding, modular MUL, Wallace MUL units within the Mod-MUL. R-S(n, k) circuit modeling of (7, 3) and one other scheme. Montgomery MUL modeled for 16, 32, 64, 128 -bit operands. Montgomery decomposed into 3 separate Integer units, realized using Wallace-tree MUL/ADDer units. Xilinx Spartan® FPGAs targeted for cost, power, performance and area tradeoffs. Davis, Wake, Leehaug & Namilae 22 227 -MAPLD 04

Lessons Learned • Design versus programming: “subjects” can be taught to explore a search space of candidate architectures to realize algorithms in programmable logic/custom computing platforms. – Design involves planning and configuration tasks in a state-space search. – Requisite knowledge burden can be minimized through use of model-based problem representation with a graphical notation as mediating interface. • Designer productivity: effort distribution data is consistent with earlier studies (Joshi et al. , 1997, Jawchinda et al. , 1999). – High productivity-design performance possible without VHDL expertise. • Designer productivity versus design performance: with careful analysis, search space can be significantly “pruned”. – Playing with problem formulation identified better “organizing principles” for architecture, changing shape of search space. – However, there is no substitute for experience (heuristic knowledge). – Furthermore, codifying heuristics and using automated “estimators” to guide selection of architecture candidates overcomes limitations in current language-based architecture compilers. Davis, Wake, Leehaug & Namilae 23 227 -MAPLD 04

Custom Computing for Mobile Computing • Executable algorithmic state machines: – Both control and datapath operations specified in “time” (cycle scheduling) and “space” (binding operations to resource types). – Basic data and memory operations supported in ASM method using datapath macro-functions and memory arrays. – Notation is directly executable in the tool set, hence, “executable” ASM. – Designer doesn’t give up design exploration or decision-making to a language compiler. • Using ASM diagrams: – A “thinking aid” for defining the structure and sequencing behavior of Finite State Machines. – Used in 3 different ways: (1) definition/specification of sequential systems, (2) analysis of sequential circuits, (3) design of combinational and sequential circuits behaviorally. – Use UML diagrams for specification (using IBM’s Rational Rose®) with architecture modeling with ASM (using Exsedia’s Nimbus. TM and IPalette. TM). – Designers were able to carry out complete design effort without knowledge of HDLs. • Algorithms, Patterns and Protocols – Directly support mapping of algorithm onto candidate architectures. – Directly support exploration of protocol implementations distributed across many concurrent threads of execution. Davis, Wake, Leehaug & Namilae 24 227 -MAPLD 04

Acknowledgements • This project was made possible with a software grant from Exsedia for use of their Nimbus software. • Additional tools from Synopsys and Xilinx were provided under a research grant from Department of Defense. • Formulation of the R-S(7, 3) is based on the coding model presented in Sklar, B. , Digital Communications: Fundemantal and Applications, 2 nd ed. , Prentice-Hall Publishers, Inc. , 2001. Davis, Wake, Leehaug & Namilae 25 227 -MAPLD 04