Design of Steel Structures Limit States Method N











































![Dynamic Effects • The draft code [IS 875 (Part 3)] stipulates that the dynamic Dynamic Effects • The draft code [IS 875 (Part 3)] stipulates that the dynamic](https://slidetodoc.com/presentation_image_h2/45a1bb760ecadbb6112723e3b7779caa/image-73.jpg)








- Slides: 84

Design of Steel Structures Limit States Method N. Subramanian © Oxford University Press 2016. All rights reserved.

Chapter 3 Loading and Load Combinations © Oxford University Press 2016. All rights reserved.

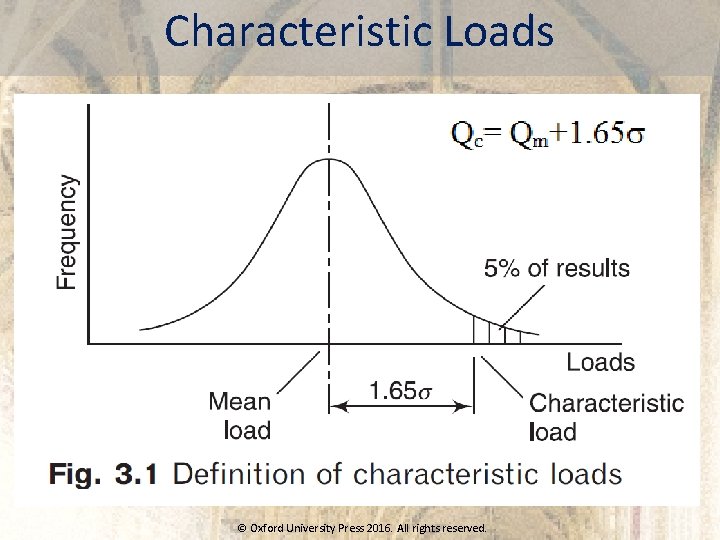
Characteristic Loads © Oxford University Press 2016. All rights reserved.

Dead Loads • A load fixed in magnitude and in position is called a dead load. • Determining the dead load of the structure requires the estimation of the weight of the structure together with its associated ‘nonstructural’ components. • Thus, the weight of bare steelwork (including items such as bolts, nuts, and weld material), slabs, beams, walls, columns, partition walls, false ceiling, cladding, water tanks, stairs, plaster finishes, and other services (cable ducts, water pipes, etc. ) are to be calculated. • Note that the dead load is not known before it is designed. Hence, an initial value is estimated based on experience. © Oxford University Press 2016. All rights reserved.

Imposed Loads • Imposed loads (previously referred to as live loads) are gravity loads other than dead loads and cover factors such as occupancy by people, movable equipment and furniture within buildings, stored materials such as books, machinery, and snow. They vary often in space and in time. • Imposed loads may be subdivided into two groups: -those which are applied gradually (may use static equivalent) -those that are applied dynamically • Imposed loads are specified in the codes (IS 875 -Part 2) based on observation and measurement. • Load due to partition: Increase the floor load by 33. 3% per metre run of partition wall subject to a minimum of 1 k. N/m 2. The total weight per metre run must be less than 4 k. N/m. © Oxford University Press 2016. All rights reserved.

Reduction in Imposed Load of Columns © Oxford University Press 2016. All rights reserved.

Imposed Load on Roofs © Oxford University Press 2016. All rights reserved.

How Real are Imposed Loads? • Srinivasa Rao and Krishnamurthy (1993) conducted a load survey on imposed loads acting on office buildings and found that the maximum imposed load is only of the order of 2. 35 k. N/ sq. m in such buildings without separate provision for store rooms. (This value is much smaller than 4 k. N/sq. m as specified in IS 875 (Part 2). ) • A similar survey was conducted by Sunil Kumar (2002), and Sunil Kumar and Kameswara Rao (1994) on residential buildings. The design imposed loads specified in the code are much higher than those estimated by the load survey © Oxford University Press 2016. All rights reserved.

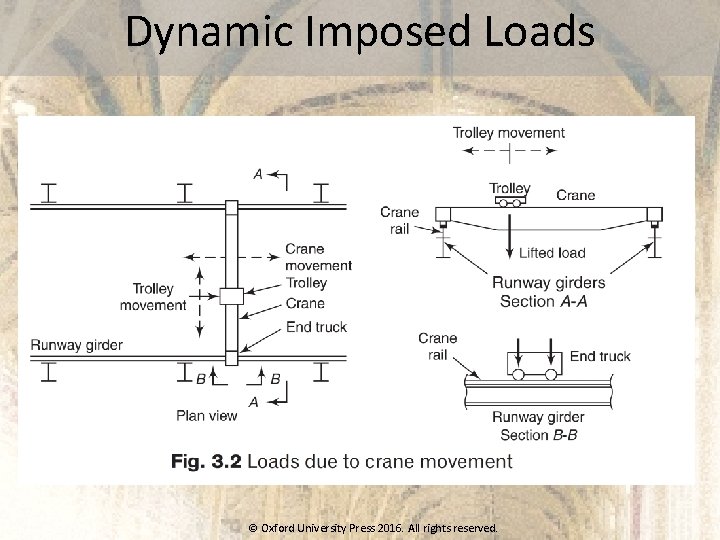
Dynamic Imposed Loads © Oxford University Press 2016. All rights reserved.

Dynamic Imposed Loads © Oxford University Press 2016. All rights reserved.

Snow Loads © Oxford University Press 2016. All rights reserved.

Snow Loads © Oxford University Press 2016. All rights reserved.

Unbalanced Snow Distribution © Oxford University Press 2016. All rights reserved.

Minimum Temperature -IS 875(Part 5) © Oxford University Press 2016. All rights reserved.

Maximum Temperature -IS 875(Part 5) © Oxford University Press 2016. All rights reserved.

Temperature Effects © Oxford University Press 2016. All rights reserved.

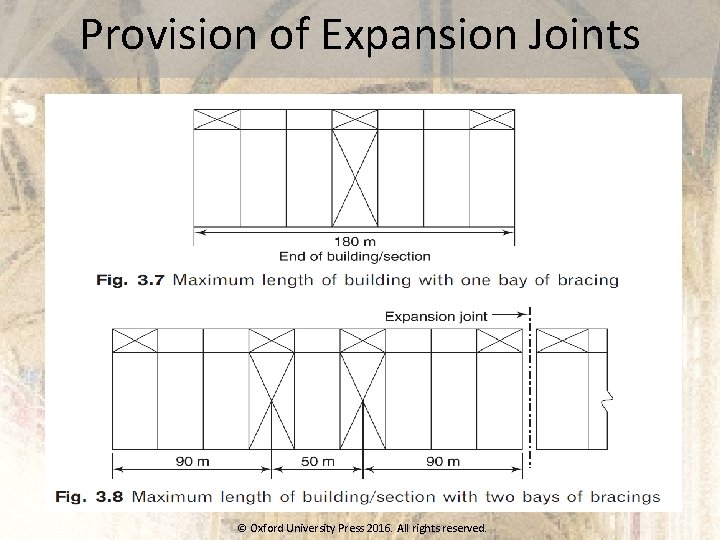
Provision of Expansion Joints © Oxford University Press 2016. All rights reserved.

Other Loads • Flood Loads • Erection Loads • Loads due to Settlement • Loads due to Ponding • Blast Loads • Creep & Shrinkage loads • Fire Loads • Fatigue Loads • Hydro-static Loads • Earth Pressure • Wave and Current Loads • Load due to Lack-of-fit • Resonant Loads • Load due to Differential Shortening of Columns • Dust Loads © Oxford University Press 2016. All rights reserved.

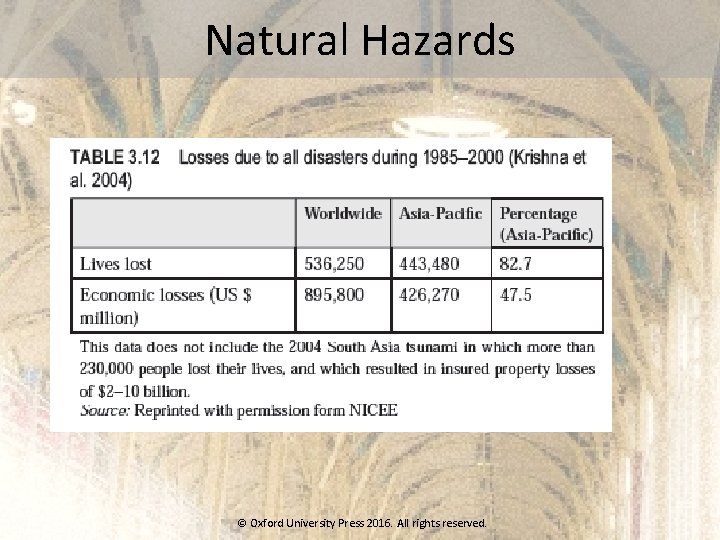
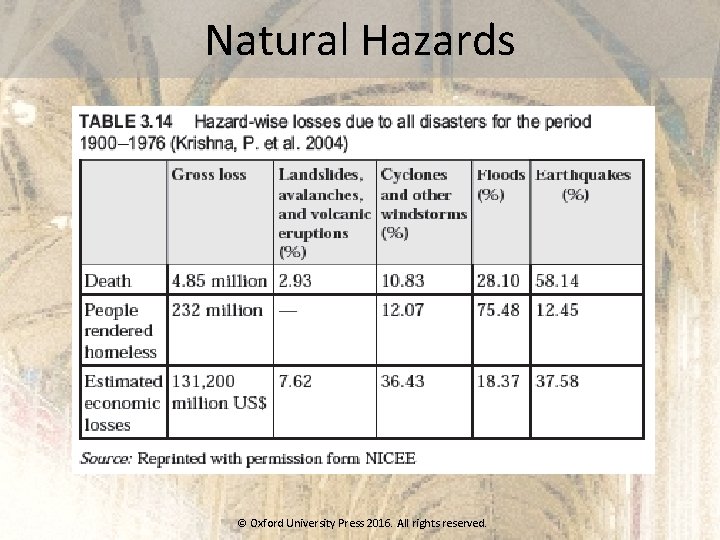
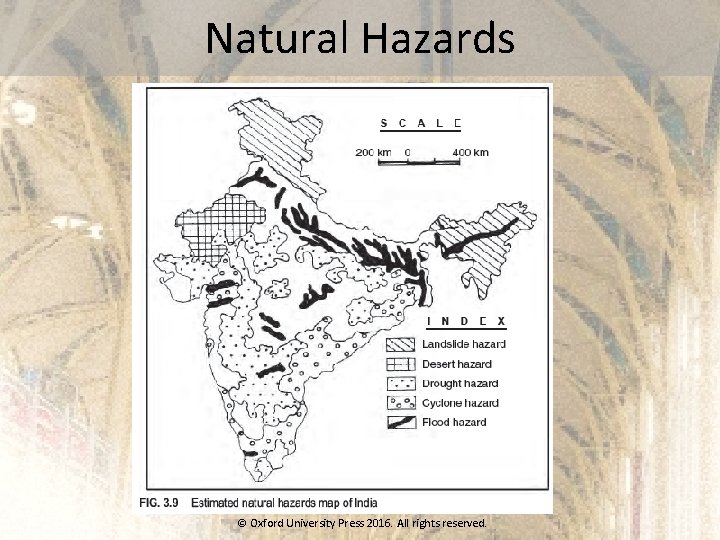
Natural Hazards © Oxford University Press 2016. All rights reserved.

Natural Hazards © Oxford University Press 2016. All rights reserved.

Natural Hazards © Oxford University Press 2016. All rights reserved.

Case Study: Chennai Floods, Dec. 2015 According to Skymet data, during the month of November, Chennai recorded a whopping 1218. 6 mm of rain – three times its usual monthly rainfall (as against annual rainfall of 1200 - 1300 mm). Again on December 1– 2, 2015, in 24 hours Chennai received 345 mm rain, which is the highest on any day since 1901. The flooding due to the rain and opening of gates of reservoirs around Chennai is the worst in a century. As of 10 December, more than 400 people have died and over 1. 8 million people have been displaced Flooding in Chennai during Dec. 2015 will cost India’s economy an estimated $3 billion in losses (worst disaster of its kind in 2015)in terms of damage to the economy. © Oxford University Press 2016. All rights reserved.

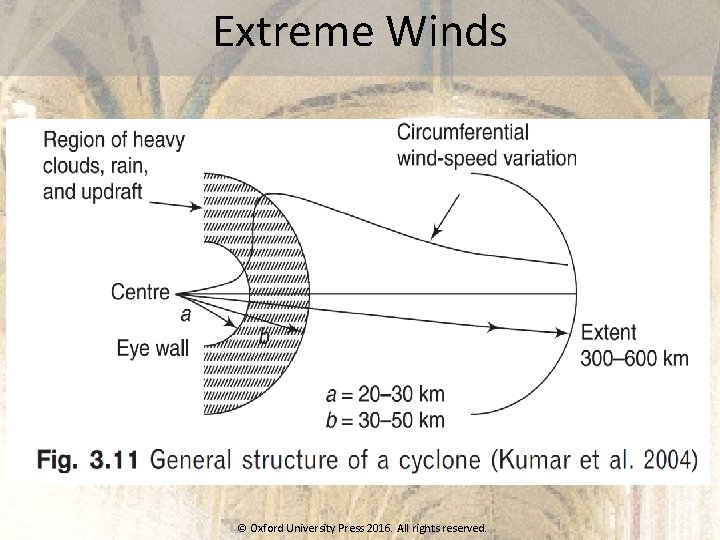
Extreme Winds © Oxford University Press 2016. All rights reserved.

Circulation of Winds © Oxford University Press 2016. All rights reserved.

Various Types of Windstorms © Oxford University Press 2016. All rights reserved.

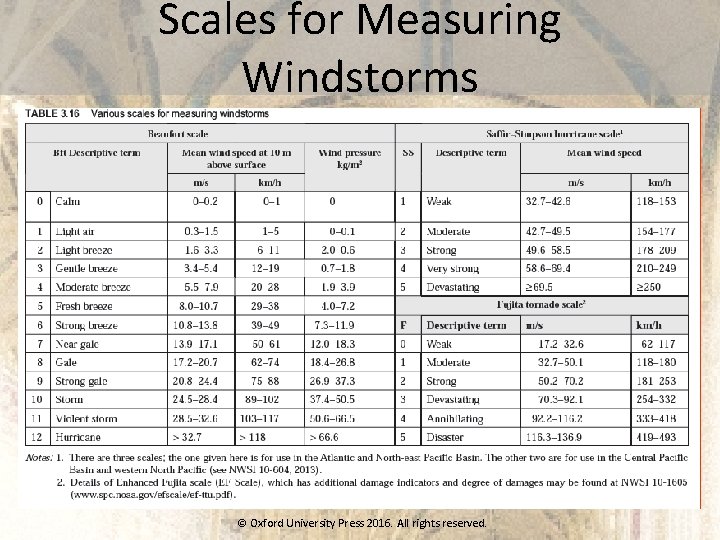
Scales for Measuring Windstorms © Oxford University Press 2016. All rights reserved.

Case Study: Hurricane Katrina, 2005 The total damage from Katrina is estimated at $81. 2 billion (2005 US dollars). Federal disaster declarations covered 233, 000 km² of the United States, an area almost as large as the United Kingdom. The hurricane left an estimated three million people without electricity. It was a category Five hurricane, on the Saffir–Simpson scale, with the highest wind speed of 280 km/h. It caused severe destruction along the Gulf coast from central Florida to Texas, much of it due to the storm surge. The storm surge breached levees, and made 80% Louisiana submerged. At least 1836 people lost their lives, making it the deadliest hurricane in the US since 1928. © Oxford University Press 2016. All rights reserved.

Case Study: Typhoon Haiyan, Philippines, 2013 The Category 5 Typhoon had winds reaching 315 km/h and became the strongest typhoon to make landfall ever recorded. The accompanying storm surge sent a wave up to five meters high. It killed 6, 201 people, 28, 626 injured(1, 785 still missing), 16 million people affected with 1. 2 million houses damaged/destroyed- property damage of $ 1. 5 billion. © Oxford University Press 2016. All rights reserved.

Variation of Wind Velocity with Height © Oxford University Press 2016. All rights reserved.

Variation of Wind Velocity with Height © Oxford University Press 2016. All rights reserved.

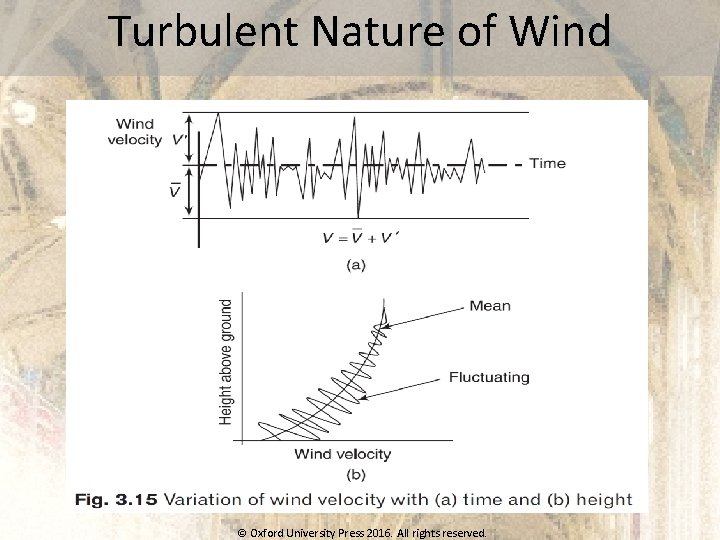
Turbulent Nature of Wind © Oxford University Press 2016. All rights reserved.

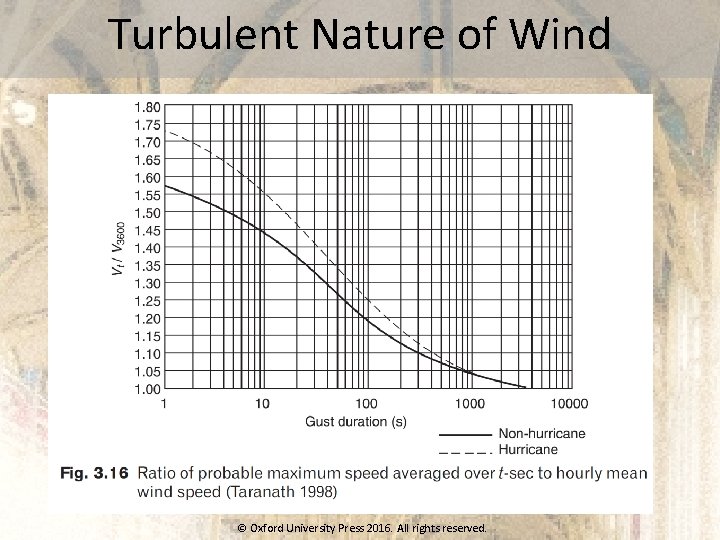
Turbulent Nature of Wind © Oxford University Press 2016. All rights reserved.

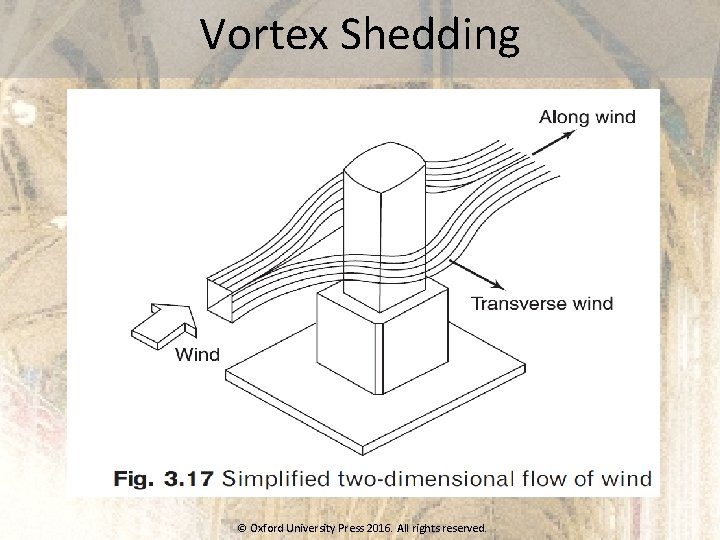
Vortex Shedding © Oxford University Press 2016. All rights reserved.

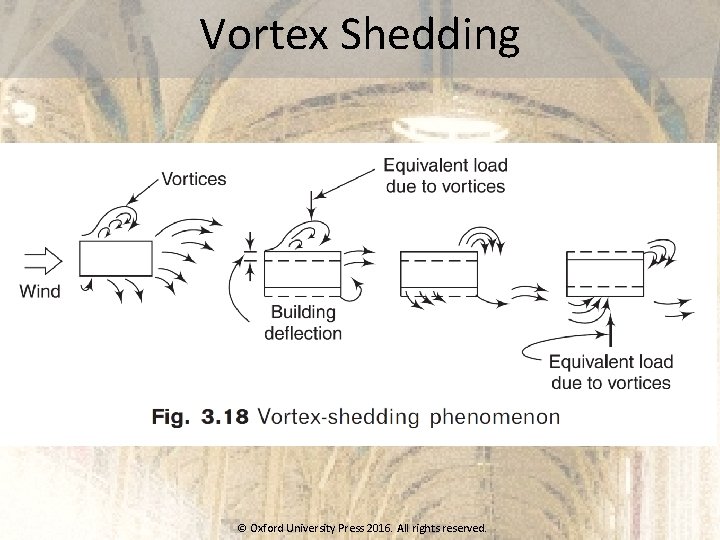
Vortex Shedding © Oxford University Press 2016. All rights reserved.

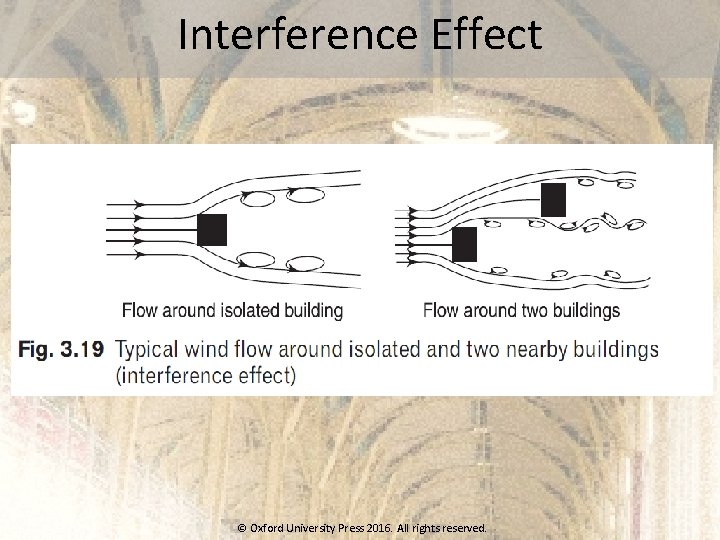
Interference Effect © Oxford University Press 2016. All rights reserved.

Wind Tunnel Tests In India also, several boundary-layer wind tunnel facilities exist, provided by NAL, Bangalore, IISc. , Bangalore, SERC Chennai, IIT Bombay, IIT Roorkee, and IIT Delhi. A small wind tunnel test may cost approximately Rs. 350, 000 © Oxford University Press 2016. All rights reserved.

Case Study: The Indian Ocean Tsunami, 2004 This second largest earthquake (magnitude 9. 1), since the 1984 Alaskan earthquake, caused an estimated 1600 km fault surface to slip under the ocean to of about 15 m, resulting in the earthquake (followed by the tsunami) to be felt simultaneously as far away as Bangladesh, Sri Lanka, India, Malaysia, Myanmar, Thailand, Singapore, and the Maldives. About 230, 000 people died (16, 000 in India), 500, 000 injured and several thousands were missing. In addition, 655, 000 people were made homeless. 1. 7 million people were displaced in 14 countries in Southeast Asia. Estimated cost of aid and reconstruction following tsunami: $7. 5 billion. © Oxford University Press 2016. All rights reserved.

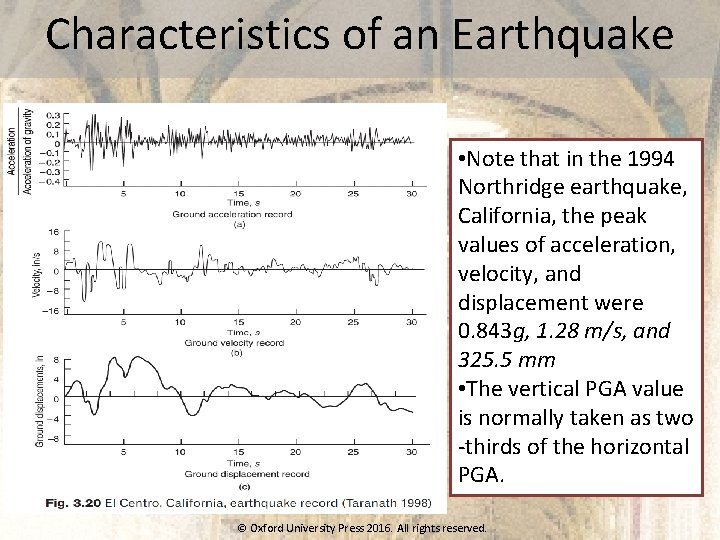
Characteristics of an Earthquake • Note that in the 1994 Northridge earthquake, California, the peak values of acceleration, velocity, and displacement were 0. 843 g, 1. 28 m/s, and 325. 5 mm • The vertical PGA value is normally taken as two -thirds of the horizontal PGA. © Oxford University Press 2016. All rights reserved.

Magnitude & Intensity of Earthquakes • The magnitude is measured on the Richter scale, which is a logarithmic scale • Note that an earthquake of magnitude 6 is 31. 6 times more powerful than one measuring 5 • Earthquakes of Richter magnitude 6, 7, and 8, respectively, are categorized as moderate, major, and great. • Although an earthquake has only one magnitude, it has many different intensities. The intensity at a place is evaluated considering the three features of shaking—perception by people, performance of buildings, and changes to natural surroundings. • Two commonly used intensity scales are: Modified Mercalli Intensity (MMI) scale and MSK scale. (See Appendix D of IS 1893) © Oxford University Press 2016. All rights reserved.

Case Study: Tohoku Earthquake, Japan, 2011 Largest ever recorded in Japan. Up to 40. 5 m tall tsunami waves (highest ever recorded in Japan). Costliest natural disaster in world history. One of the five most powerful earthquakes in the world since modern record. Killed an estimated 15, 889 persons, 6152 injured, and 2611 people missing. 127, 290 buildings totally collapsed, 272, 788 half-collapsed, and 747, 989 partially damaged. Extensive structural damage to Fukushima-Daiichi nuclear reactors. Economic losses estimated at US$ 235 billion © Oxford University Press 2016. All rights reserved.

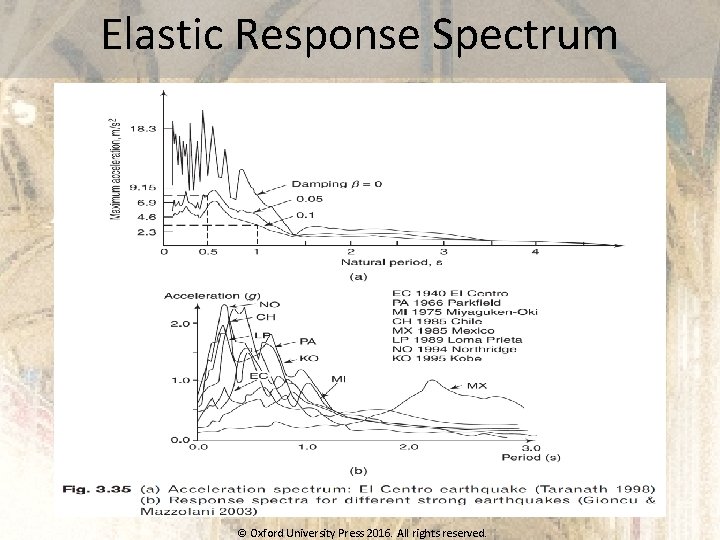
Elastic Response Spectrum © Oxford University Press 2016. All rights reserved.

Elastic Response Spectrum © Oxford University Press 2016. All rights reserved.

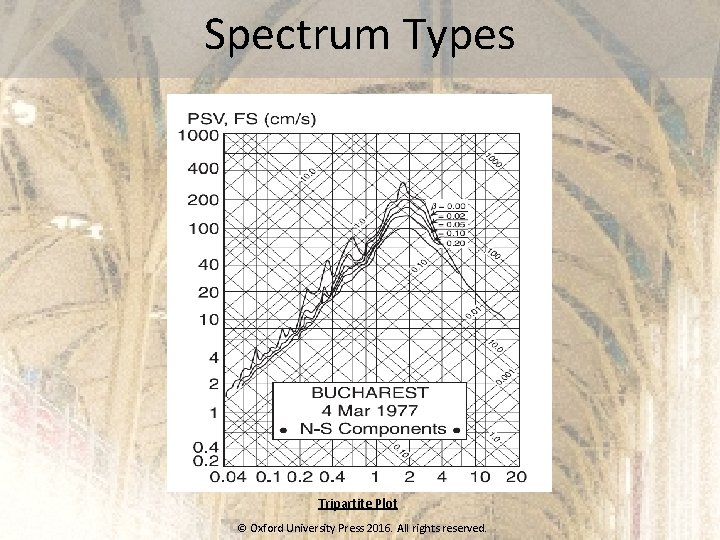
Spectrum Types Tripartite Plot © Oxford University Press 2016. All rights reserved.

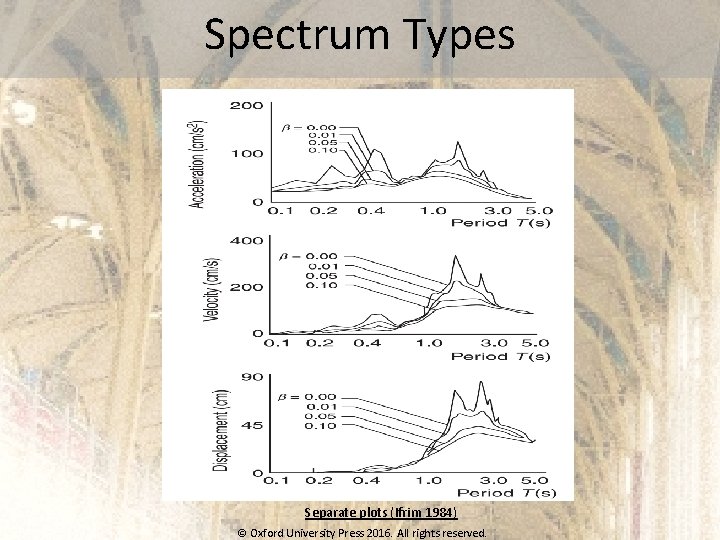
Spectrum Types Separate plots (Ifrim 1984) © Oxford University Press 2016. All rights reserved.

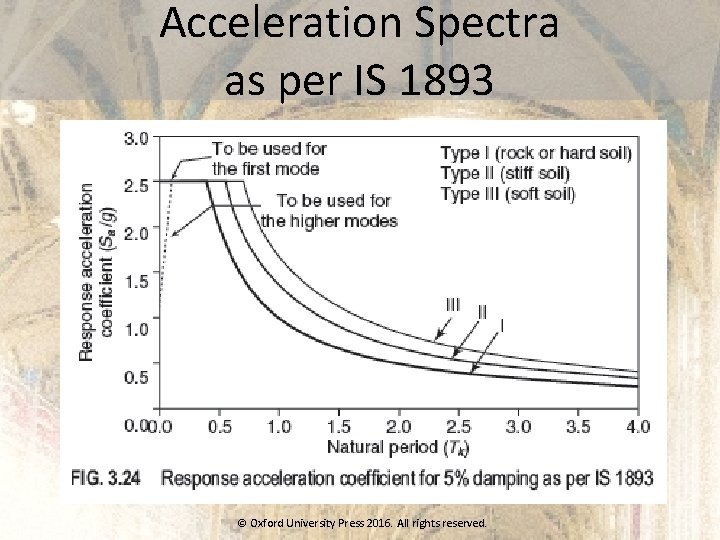
Acceleration Spectra as per IS 1893 © Oxford University Press 2016. All rights reserved.

Multiplication Factors for other Damping Values © Oxford University Press 2016. All rights reserved.

Determination of Earthquake Forces © Oxford University Press 2016. All rights reserved.

Seismic Design Philosophy • Minor and frequent earthquakes should not cause any damage to the structure. • Moderate earthquakes should not cause significant structural damage but could have some non-structural damage (the structure should be operational once the damaged members are repaired). • Major and infrequent earthquakes should not cause collapse but will stand so that people can be evacuated and property recovered. • Hence the structures are designed for much smaller forces than actual seismic loads during strong ground shaking. Note that this approach is different than that adopted in the case of wind, dead, live, and other loads, where the structure is designed for the anticipated loads © Oxford University Press 2016. All rights reserved.

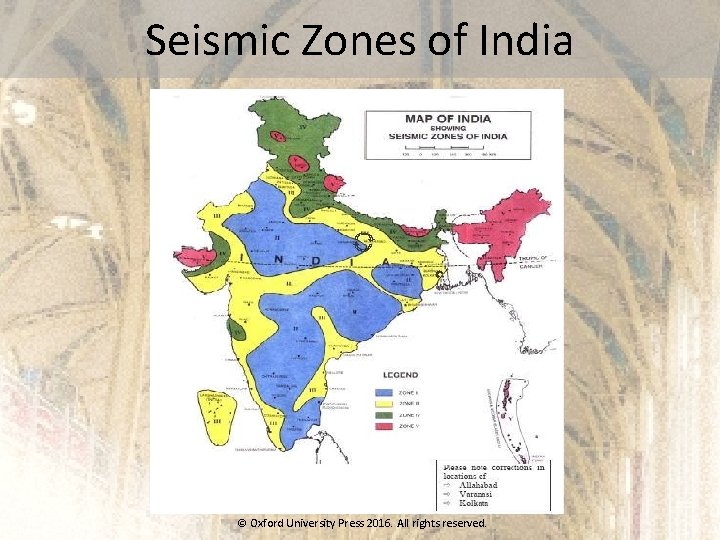
Seismic Zones of India © Oxford University Press 2016. All rights reserved.

Requirement of Dynamic Analysis © Oxford University Press 2016. All rights reserved.

Equivalent Lateral Base Shear Force Procedure The equivalent lateral base shear force procedure has traditionally been used by several building codes to simplify the design process. (This procedure is applied to regular structures only. ) As per the code (IS 1893) the design horizontal seismic coefficient for a structure is I= Importance Factor (1. 0 to 1. 5) R=Response Reduction Factor © Oxford University Press 2016. All rights reserved.

Requirement of Dynamic Analysis © Oxford University Press 2016. All rights reserved.

Equivalent Static Method The total design seismic base shear if determined by: K =2 © Oxford University Press 2016. All rights reserved.

Reduction in Imposed Load © Oxford University Press 2016. All rights reserved.

Mass to be Considered © Oxford University Press 2016. All rights reserved.

Approximate Natural Period The approximate fundamental natural period of vibration, in seconds, for a moment-resisting frame without brick infill panels is given by the code For all other buildings, including moment resisting frame buildings with brick infill: © Oxford University Press 2016. All rights reserved.

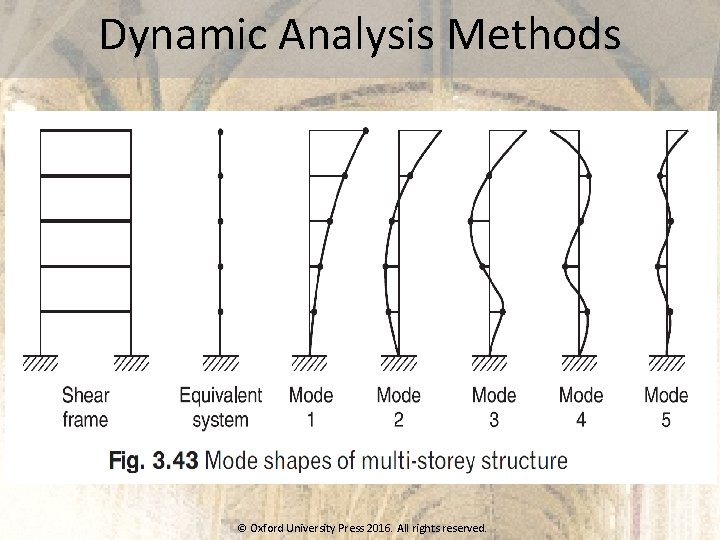
Dynamic Analysis Methods • Response Spectrum Method • Time History Method © Oxford University Press 2016. All rights reserved.

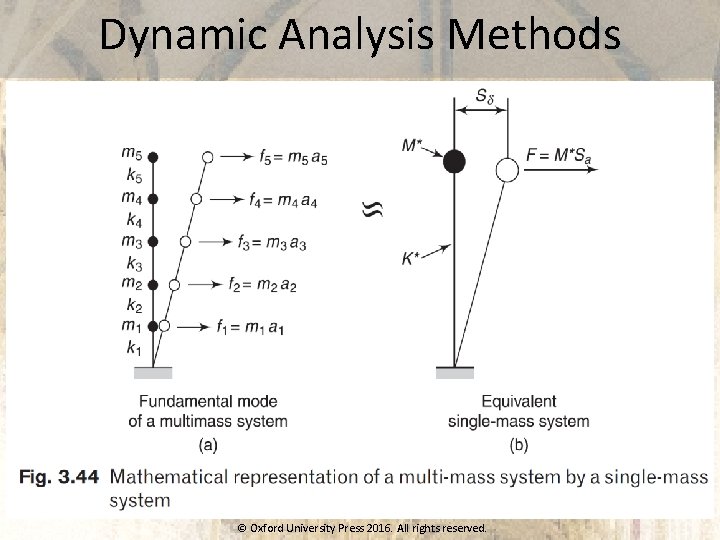
Dynamic Analysis Methods © Oxford University Press 2016. All rights reserved.

Dynamic Analysis Methods © Oxford University Press 2016. All rights reserved.

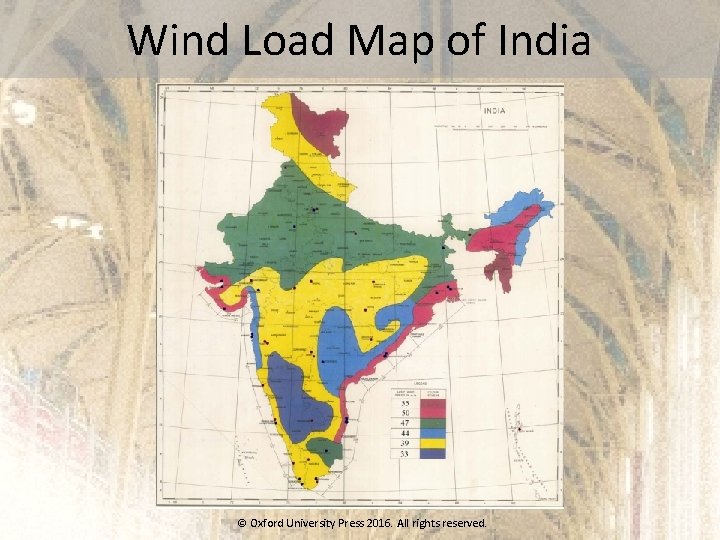
Wind Load Map of India © Oxford University Press 2016. All rights reserved.

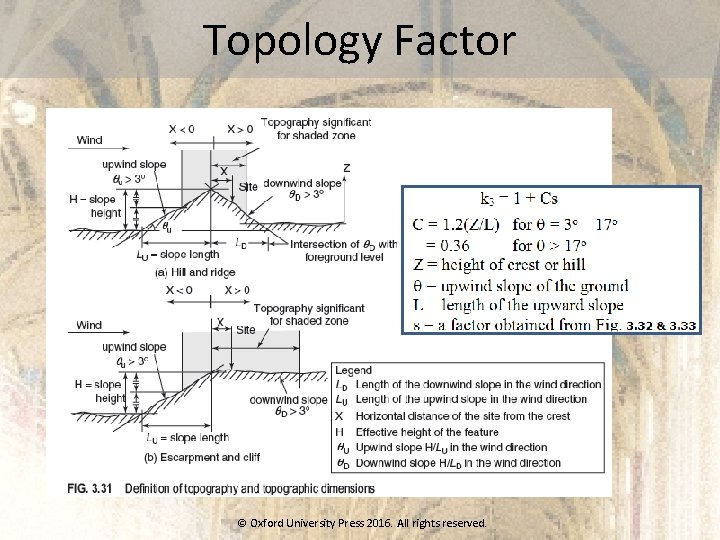
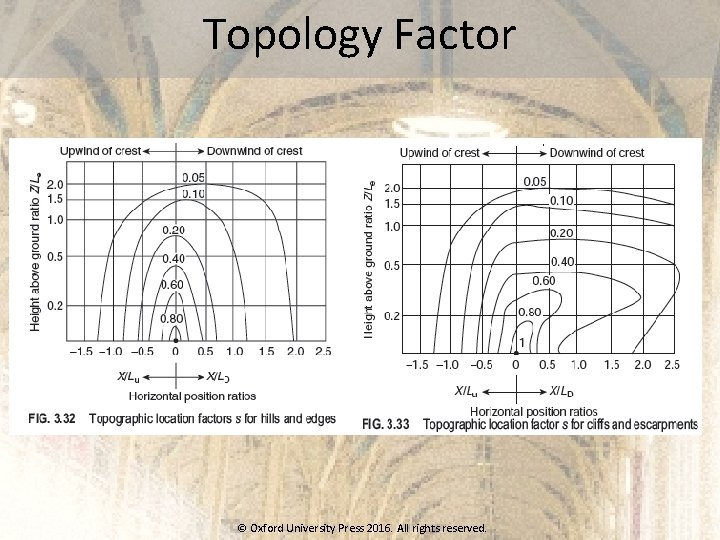
Design Wind Speed The design wind speed is obtained from the basic wind speed shown in Fig. 3. 30, after modifying it to include risk level, terrain roughness, height and size of structure, and local topography as © Oxford University Press 2016. All rights reserved.

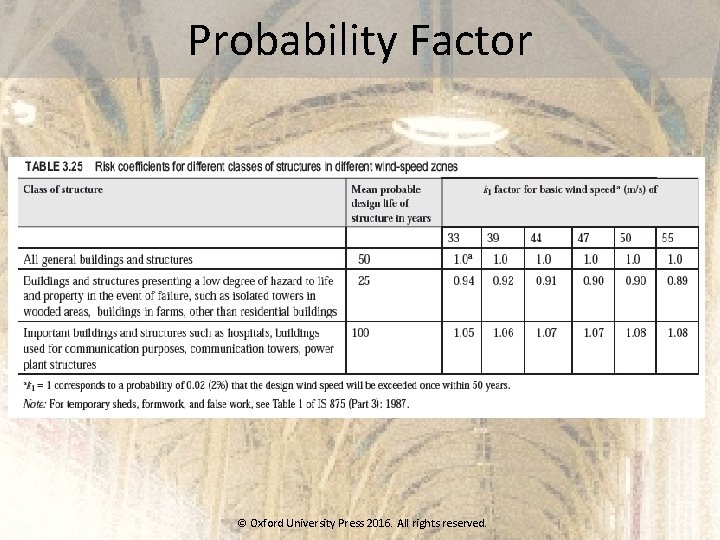
Probability Factor © Oxford University Press 2016. All rights reserved.

Terrain & Height Factor © Oxford University Press 2016. All rights reserved.

Topology Factor © Oxford University Press 2016. All rights reserved.

Topology Factor © Oxford University Press 2016. All rights reserved.

Importance factor for Cyclonic Regions In order to ensure greater safety of structures located within regions 60 km wide of the east coast as well as on the Gujarat coast (wind speed > 70 m/s during cyclones), the following values of k 4 are given in the draft code and IS 15498: 2004. © Oxford University Press 2016. All rights reserved.

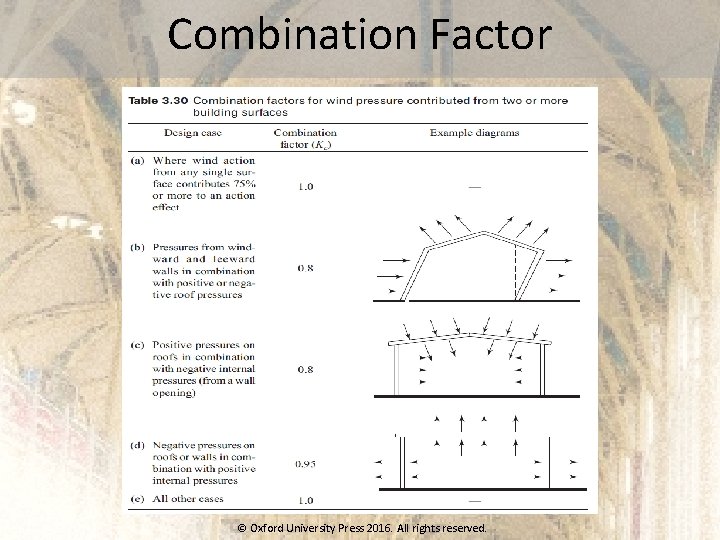
Combination Factor © Oxford University Press 2016. All rights reserved.

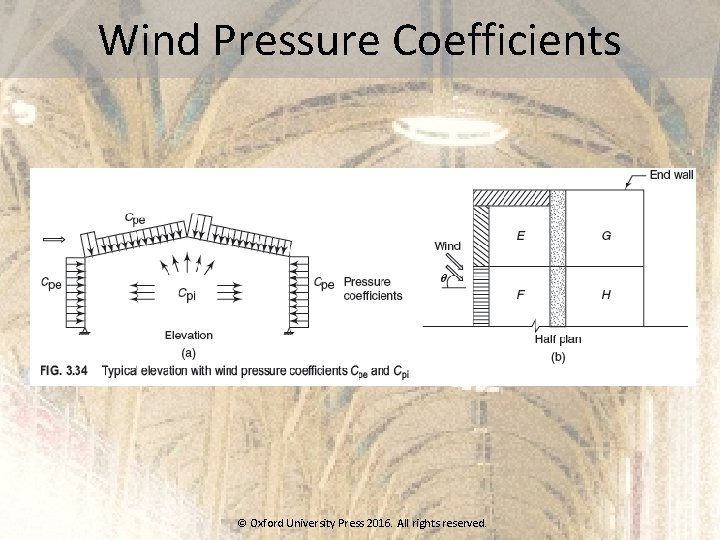
Wind Pressure Coefficients © Oxford University Press 2016. All rights reserved.

External Pressure Coefficients for Pitched Roofs © Oxford University Press 2016. All rights reserved.

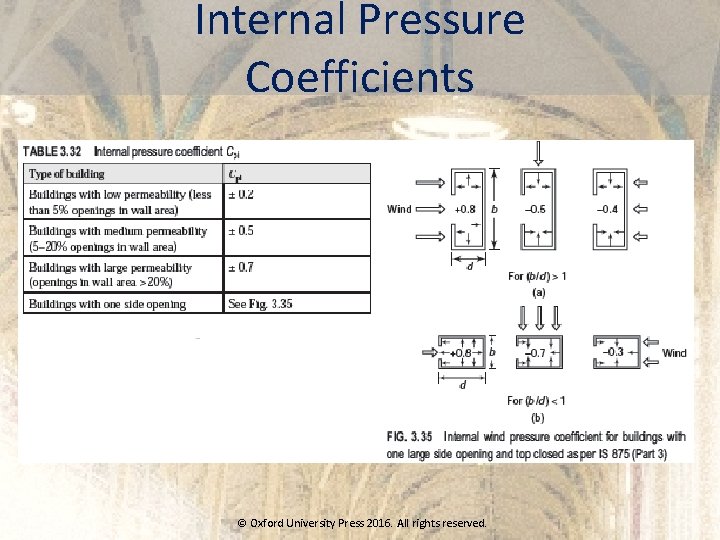
Internal Pressure Coefficients © Oxford University Press 2016. All rights reserved.

Frictional Drag To be calculated only where the ratio d/h or d/b is greater than 4. The frictional drag force, F′, in the direction of the wind is given by the following formulae. © Oxford University Press 2016. All rights reserved.

Interference Effects Interference is governed by a large number of geometrical parameters (such as shape, size, relative distance, and orientation between the structures involved) and flow parameters [wind direction, angle of attack, Strouhal number, or Reynolds number (in the case of rounded bodies)]. The draft IS 875 (Part 3) code gives a non-dimensional wind interference factor (IF), which should be used as a multiplying factor to be applied to the design wind pressure/force © Oxford University Press 2016. All rights reserved.
![Dynamic Effects The draft code IS 875 Part 3 stipulates that the dynamic Dynamic Effects • The draft code [IS 875 (Part 3)] stipulates that the dynamic](https://slidetodoc.com/presentation_image_h2/45a1bb760ecadbb6112723e3b7779caa/image-73.jpg)
Dynamic Effects • The draft code [IS 875 (Part 3)] stipulates that the dynamic effects of winds (excitations along and across the direction of the wind) should be studied for the following types of buildings (flexible slender buildings) and closed structures: 1. Those with a height to minimum lateral dimension ratio of more than 5. 0 (h/b > 5. 0) 2. Those whose fundamental natural frequency (first mode) is less than 1. 0 Hz • For these buildings, the calculated wind pressure at height z should be multiplied by the dynamic response factor Cdyn (instead of the gust factor G as suggested in the 1987 version of the code). For structures whose natural frequency in the first mode is more than 1 Hz, the dynamic response factor Cdyn may be taken as 0. 9. © Oxford University Press 2016. All rights reserved.

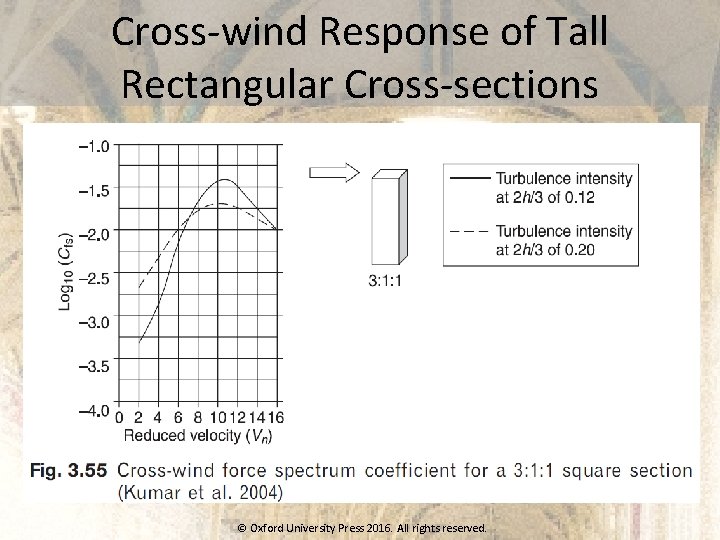
Cross-wind Response of Tall Rectangular Cross-sections © Oxford University Press 2016. All rights reserved.

Cross-wind Response of Tall Rectangular Cross-sections © Oxford University Press 2016. All rights reserved.

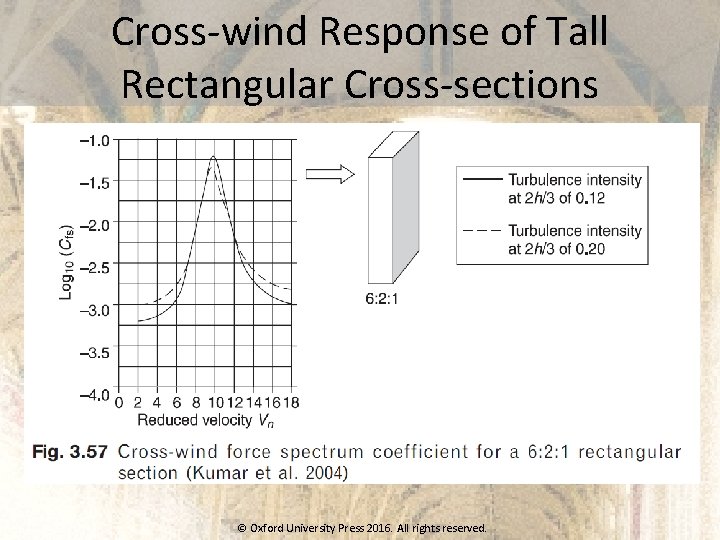
Cross-wind Response of Tall Rectangular Cross-sections © Oxford University Press 2016. All rights reserved.

Cross-wind Response of Tall Rectangular Cross-sections © Oxford University Press 2016. All rights reserved.

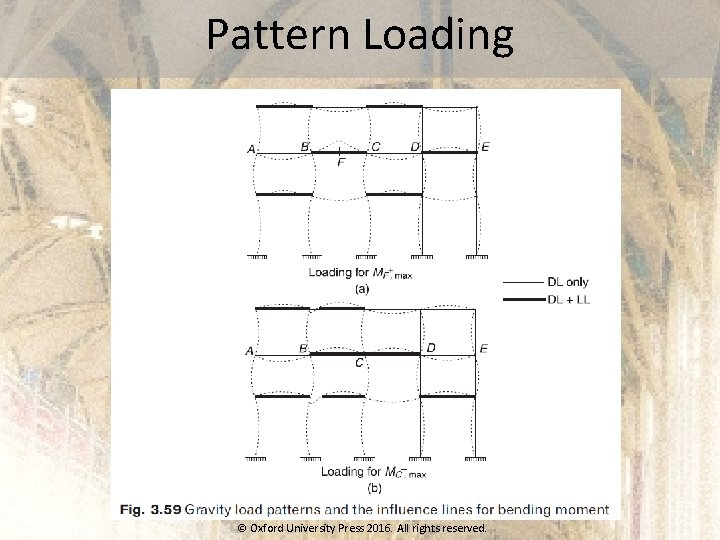
Pattern Loading © Oxford University Press 2016. All rights reserved.

Load Combinations In general, we have the following load combinations: © Oxford University Press 2016. All rights reserved.

Load Combinations © Oxford University Press 2016. All rights reserved.

Load Combination for Non-orthogonal Buildings Since the directions of earthquake forces are reversible, the following eight additional possibilities result. © Oxford University Press 2016. All rights reserved.

Conclusion Ø The four main phases in a structural design process are (i) Determining the structural system, (ii) Calculating the various loads acting on the system, (iii)Analyzing the structural system for these loads, and (iv)Designing the various members as per the codal provisions. Ø Of these, determining the various loads is the most difficult and important phase, since the final design is based on them. Ø One of the main reasons for several failures is the lack of consideration of the loads acting on the structures. © Oxford University Press 2016. All rights reserved.

Conclusion Ø Though dead loads can be evaluated accurately, Ø determining imposed, wind, and earthquake loads is difficult due to their uncertain probability of occurrence. Ø Some loads such as impact loads due to traffic on a bridge, crane loads, wind loads, and earthquake loads are dynamic in nature. Ø However, most often they are converted to equivalent static loads. Ø Dynamic analysis is resorted to only in the case of flexible structures, whose natural frequency in the first mode is less than 1. 0 Hz or whose height to least lateral dimension ratio is more than about 5. Ø Complicated structures should be avoided, especially in earthquake zones, since their analysis and modeling is difficult. © Oxford University Press 2016. All rights reserved.

Conclusion Ø For structures with complicated geometries, wind loading parameters should be derived from modal analysis in wind tunnels. Ø It is very important to realize that the earthquake codes require the designer to design the structure only to a fraction of the load that may act on the building. Ø Hence the designer has to detail the structure in such a way that, during a major earthquake, the structure may be damaged, but the occupants are able to escape on account of the ductility of the material and over-strength factors. © Oxford University Press 2016. All rights reserved.