Design of Robust and Flexible Onchip AnalogtoDigital Conversion

Design of Robust and Flexible On-chip Analog-to-Digital Conversion Architecture Ph. D. Dissertation Proposal Presentation of Daeik Kim Advisor : Prof. Martin Brooke School of Electrical and Computer Engineering Georgia Institute of Technology

Overview • • • Background Literature review Research proposal Preliminary research Future research Conclusion 2

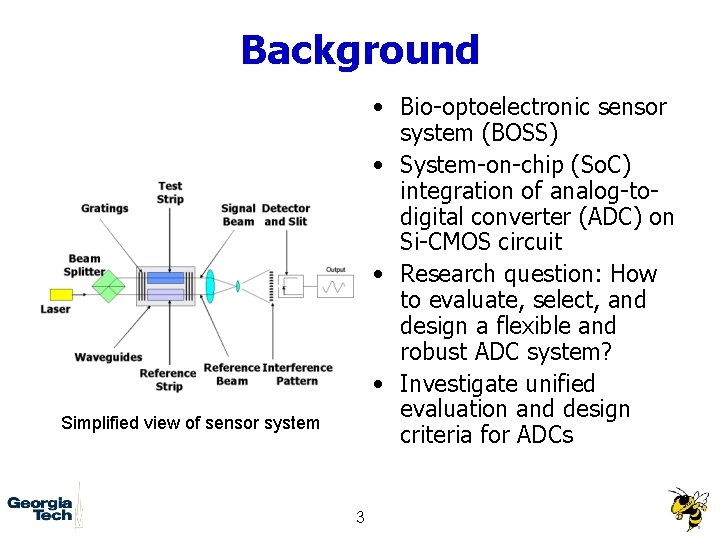
Background • Bio-optoelectronic sensor system (BOSS) • System-on-chip (So. C) integration of analog-todigital converter (ADC) on Si-CMOS circuit • Research question: How to evaluate, select, and design a flexible and robust ADC system? • Investigate unified evaluation and design criteria for ADCs Simplified view of sensor system 3

Literature Review • • Nyquist ADC Delta-sigma oversampling ADC Noise characterization Signal modeling 4

Nyquist ADC • Nyquist sampling theorem: sampling rate should be more than twice of maximum signal frequency for a lossless sampling • Examples of Nyquist ADCs – Single-slope ADC – Dual-slope ADC – Iterative algorithmic ADC – Flash ADC • Combinational ADC • Error in ADC 5

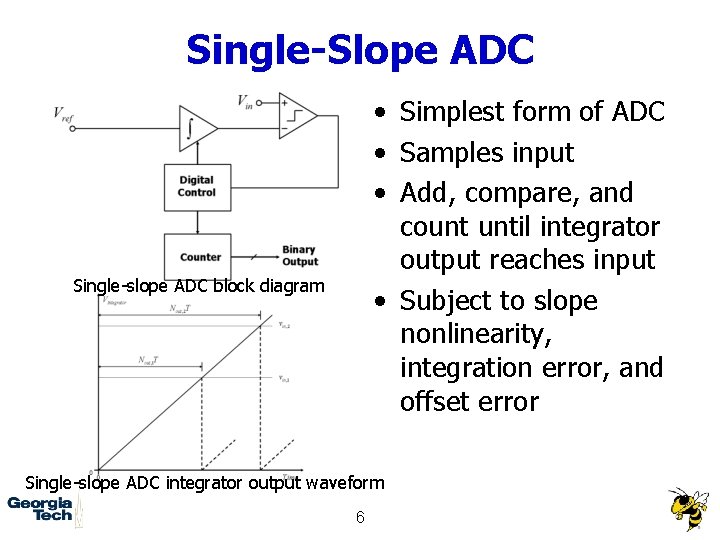
Single-Slope ADC • Simplest form of ADC • Samples input • Add, compare, and count until integrator output reaches input • Subject to slope nonlinearity, integration error, and offset error Single-slope ADC block diagram Single-slope ADC integrator output waveform 6

Dual-Slope Converter • Uses up and down slope to cancel slope nonlinearity, integration error, and offset error • Takes twice time than single-slope converter • Idea extends to tripleslope converter, etc. Dual-slope ADC block diagram Dual-slope ADC integrator output waveform 7

Iterative Algorithmic Converter • Performs binary encoding algorithm • Error in early stage propagates with multiplication • Requires high-accuracy matched parasitic components • Error – Offset and gain error in comparator and op-amp – Reference – Inaccurate multiplication and subtraction Algorithmic ADC block diagram 8

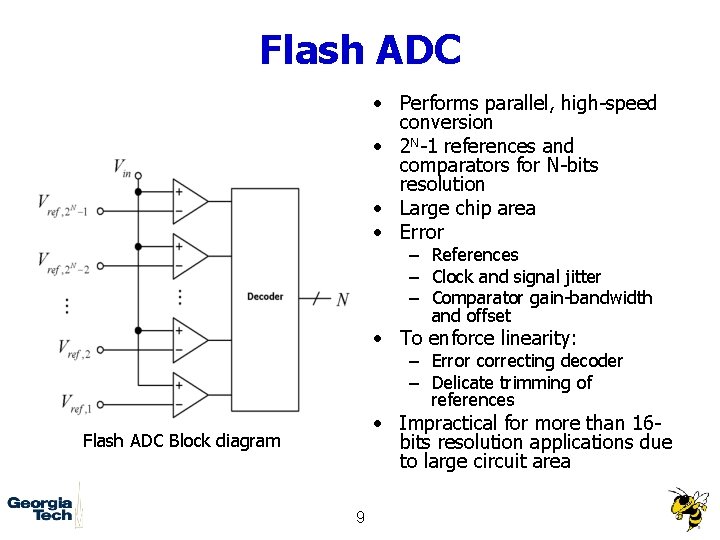
Flash ADC • Performs parallel, high-speed conversion • 2 N-1 references and comparators for N-bits resolution • Large chip area • Error – References – Clock and signal jitter – Comparator gain-bandwidth and offset • To enforce linearity: – Error correcting decoder – Delicate trimming of references • Impractical for more than 16 bits resolution applications due to large circuit area Flash ADC Block diagram 9

Combinational ADC • Mix of linear, binary, and flash conversion with time and space multiplexing is used as a tradeoff between power, speed, chip area, and resolution • Examples – – – Successive approximation ADC Single-bit iterative pipelined ADC Multi-bit pipelined ADC Interpolating ADC Folding ADC Time-interleaved ADC 10

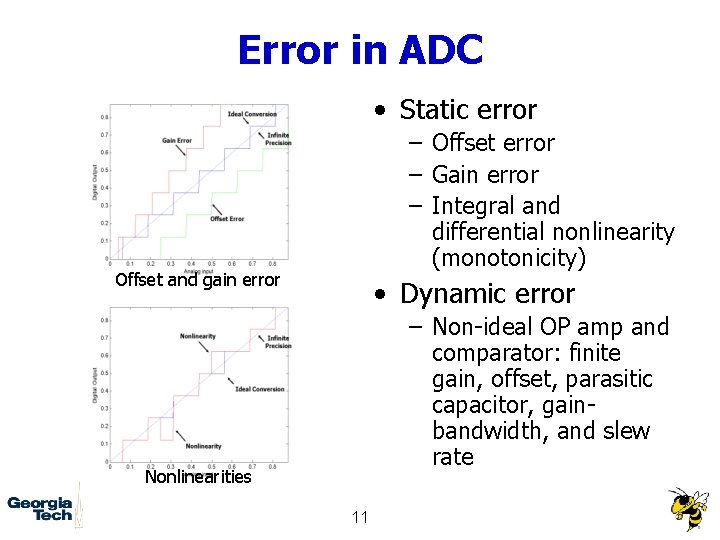
Error in ADC • Static error – Offset error – Gain error – Integral and differential nonlinearity (monotonicity) Offset and gain error • Dynamic error – Non-ideal OP amp and comparator: finite gain, offset, parasitic capacitor, gainbandwidth, and slew rate Nonlinearities 11

Delta-Sigma Oversampling ADC • • • Frequency normalization Quantization noise Oversampling Delta modulation Noise shaping Linear analysis Filtering and downsampling Issues Variations 12

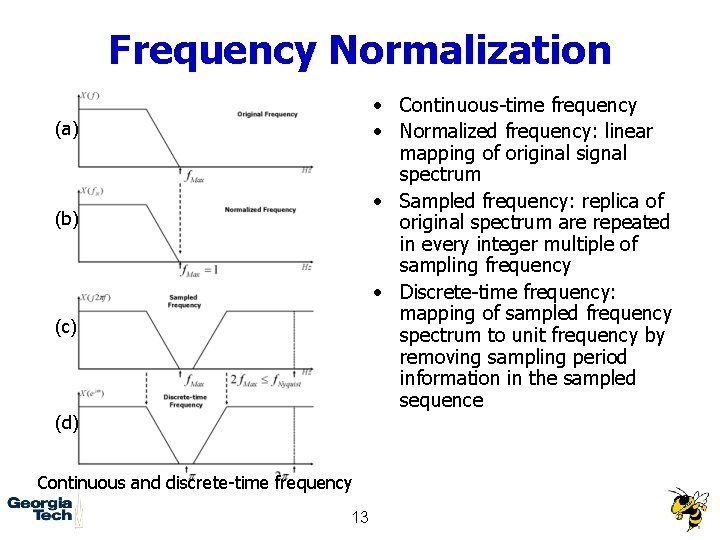
Frequency Normalization • Continuous-time frequency • Normalized frequency: linear mapping of original signal spectrum • Sampled frequency: replica of original spectrum are repeated in every integer multiple of sampling frequency • Discrete-time frequency: mapping of sampled frequency spectrum to unit frequency by removing sampling period information in the sampled sequence (a) (b) (c) (d) Continuous and discrete-time frequency 13

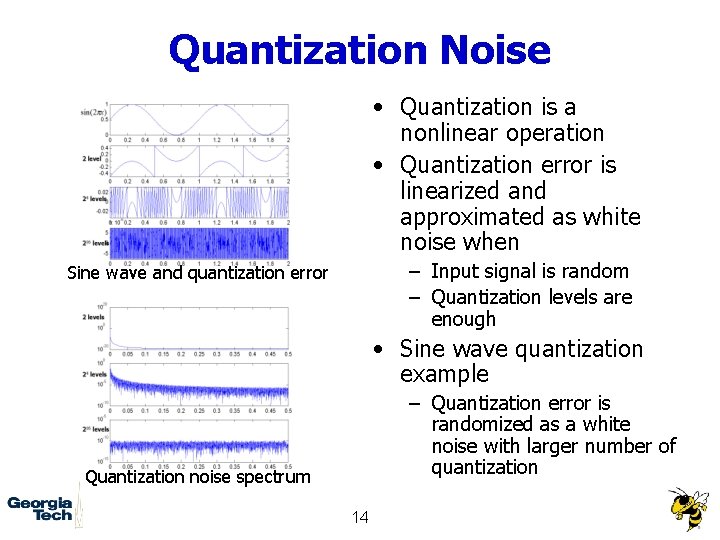
Quantization Noise • Quantization is a nonlinear operation • Quantization error is linearized and approximated as white noise when – Input signal is random – Quantization levels are enough Sine wave and quantization error • Sine wave quantization example – Quantization error is randomized as a white noise with larger number of quantization Quantization noise spectrum 14

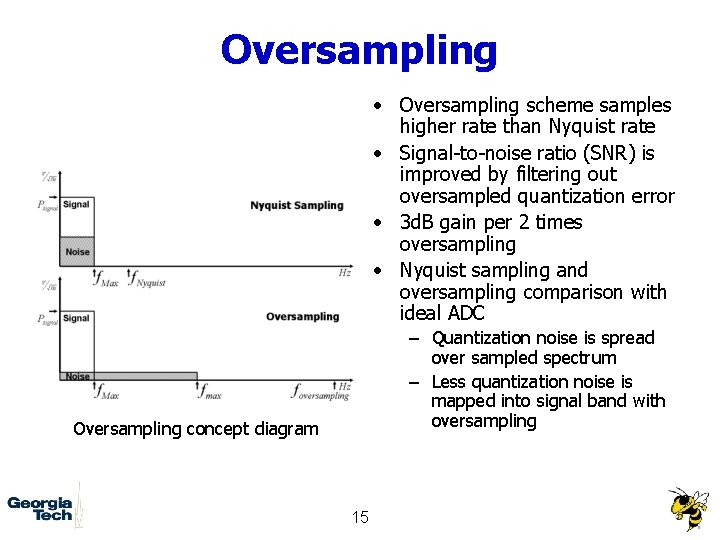
Oversampling • Oversampling scheme samples higher rate than Nyquist rate • Signal-to-noise ratio (SNR) is improved by filtering out oversampled quantization error • 3 d. B gain per 2 times oversampling • Nyquist sampling and oversampling comparison with ideal ADC – Quantization noise is spread over sampled spectrum – Less quantization noise is mapped into signal band with oversampling Oversampling concept diagram 15

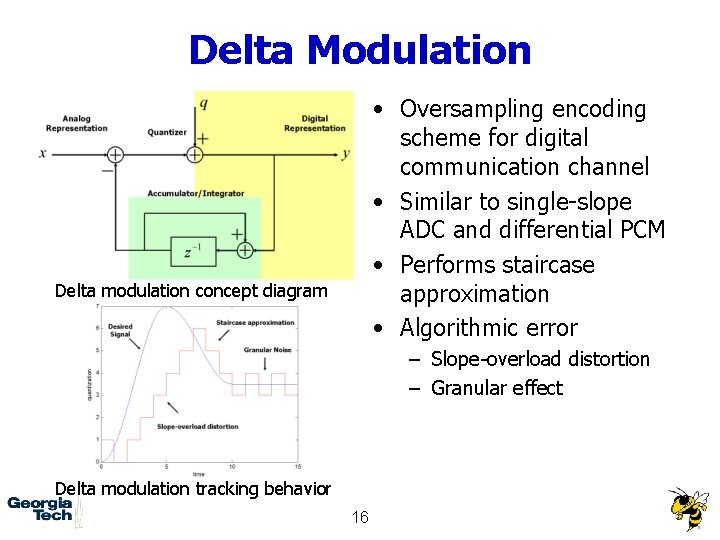
Delta Modulation • Oversampling encoding scheme for digital communication channel • Similar to single-slope ADC and differential PCM • Performs staircase approximation • Algorithmic error Delta modulation concept diagram – Slope-overload distortion – Granular effect Delta modulation tracking behavior 16

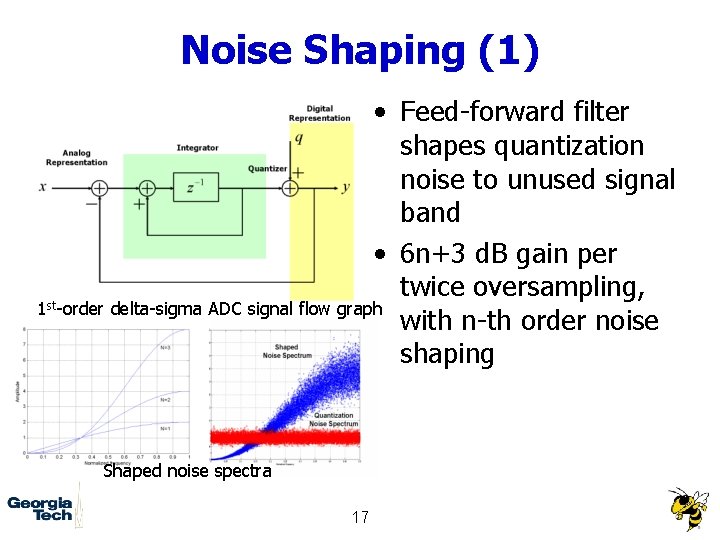
Noise Shaping (1) • Feed-forward filter shapes quantization noise to unused signal band • 6 n+3 d. B gain per twice oversampling, st 1 -order delta-sigma ADC signal flow graph with n-th order noise shaping Shaped noise spectra 17

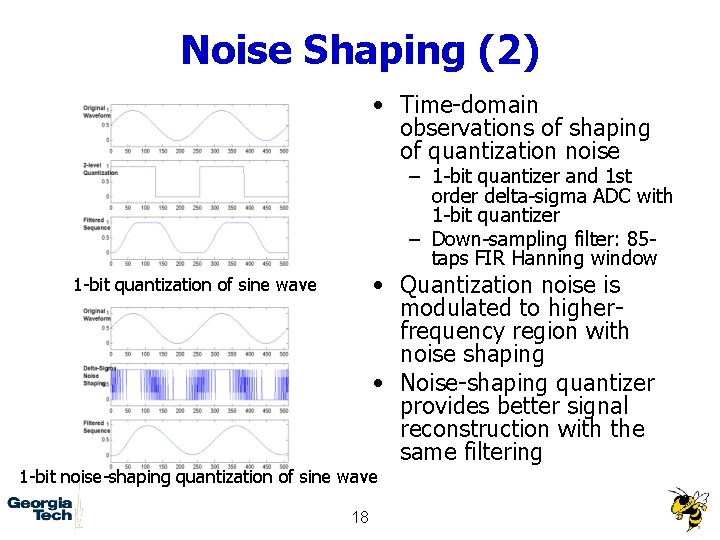
Noise Shaping (2) • Time-domain observations of shaping of quantization noise – 1 -bit quantizer and 1 st order delta-sigma ADC with 1 -bit quantizer – Down-sampling filter: 85 taps FIR Hanning window • Quantization noise is modulated to higherfrequency region with noise shaping • Noise-shaping quantizer provides better signal reconstruction with the same filtering 1 -bit quantization of sine wave 1 -bit noise-shaping quantization of sine wave 18

Linear Analysis • 1~6 th order delta-sigma modulators have been implemented based on linear approximation • Linear analysis provides good performance estimation for higher oversampling ratio (OSR) • In practice, OSR is above 64 since linear approximation does not hold for lower ratio Theoretical SNR with linear model 19

Filtering and Downsampling • Linear filters – Designed in frequency domain with linear approximation – 1~4 th order comb (sinc) filters – Various sub-optimal filters • Nonlinear dc level decoding schemes – Modeling of internal states and observation of time domain behavior – Cyclic model decoding – Autocorrelation method – Zoomer algorithm – Viterbi decoding • Nonlinear band-limited signal reconstruction algorithms – Based on projection on convex set (POCS) and singular value decomposition (SVD) 20

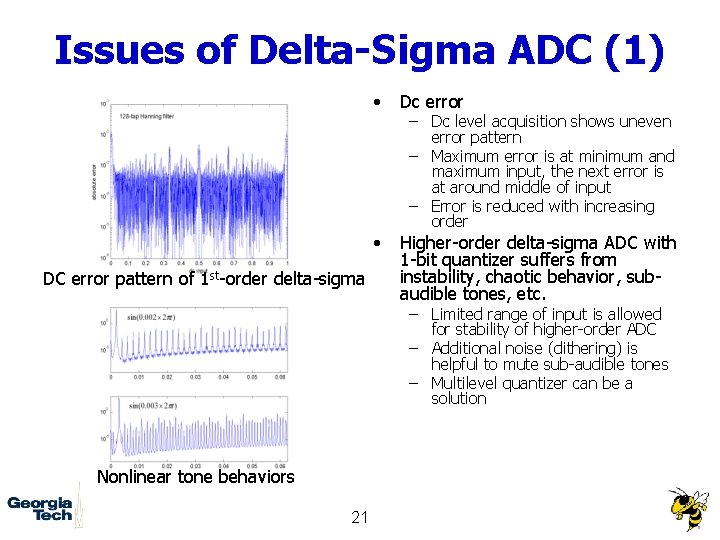
Issues of Delta-Sigma ADC (1) DC error pattern of 1 st-order delta-sigma • Dc error • Higher-order delta-sigma ADC with 1 -bit quantizer suffers from instability, chaotic behavior, subaudible tones, etc. – Dc level acquisition shows uneven error pattern – Maximum error is at minimum and maximum input, the next error is at around middle of input – Error is reduced with increasing order – Limited range of input is allowed for stability of higher-order ADC – Additional noise (dithering) is helpful to mute sub-audible tones – Multilevel quantizer can be a solution Nonlinear tone behaviors 21

Issues of Delta-Sigma ADC (2) • Nonlinear state space representation is useful for modeling time domain behavior • Nonlinear state space variable trajectories are useful for characterization of converter • In spite of problems, 1 -bit quantizer is preferred to avoid integral and differential nonlinearity error in feedback DAC Linear state space representation Nonlinear state space representation State space variable trajectory of 2 nd-order delta-sigma ADC 22

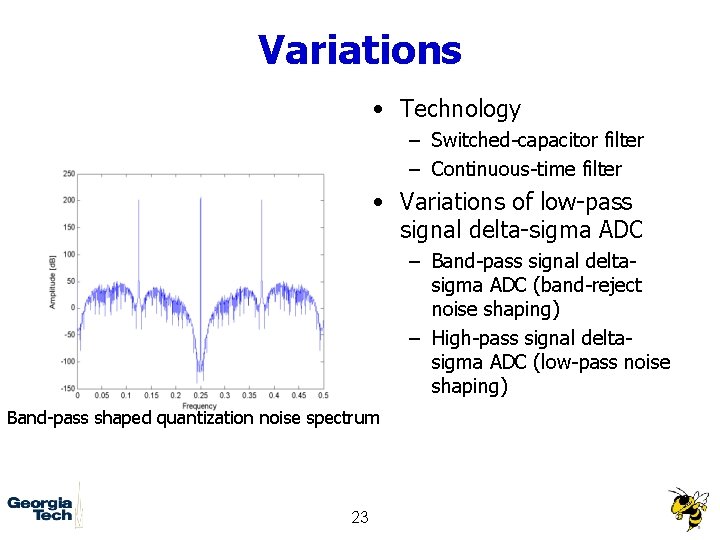
Variations • Technology – Switched-capacitor filter – Continuous-time filter • Variations of low-pass signal delta-sigma ADC – Band-pass signal deltasigma ADC (band-reject noise shaping) – High-pass signal deltasigma ADC (low-pass noise shaping) Band-pass shaped quantization noise spectrum 23

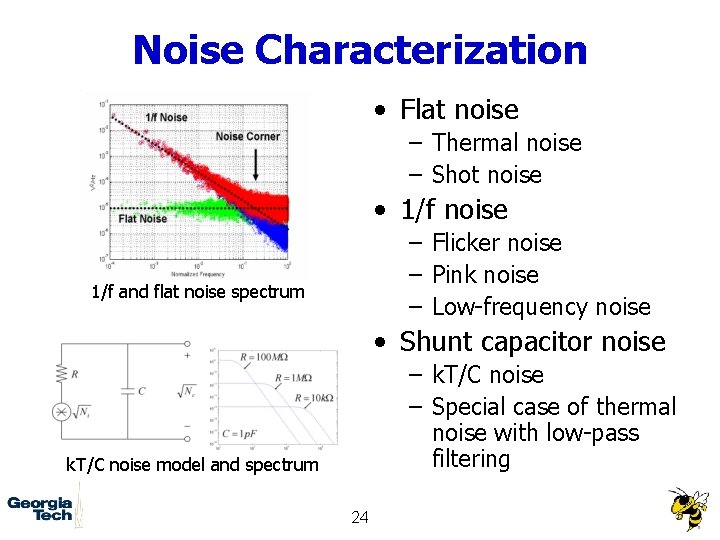
Noise Characterization • Flat noise – Thermal noise – Shot noise • 1/f noise – Flicker noise – Pink noise – Low-frequency noise 1/f and flat noise spectrum • Shunt capacitor noise – k. T/C noise – Special case of thermal noise with low-pass filtering k. T/C noise model and spectrum 24

Signal Modeling • Linear prediction coefficient (LPC) modeling performs better than filter bank modeling in general • Auto-regressive movingaverage (ARMA) modeling provides frequency-domain formulation with time-domain solution ARMA signal modeling – Pade, Prony, Shank • Levinson-(Durbin) recursion – – – Multi-pulse all-pole modeling of voice 25 Easy computation Stable Scalable Equivalent to lattice filter Less sensitive to coefficient error introduced by quantization than canonic forms

Research Proposal (1) • Investigate unified evaluation and design criteria for ADCs – Comparison on Nyquist sampling and oversampling ADCs with regard to flexibility, robustness, and system-on-chip integration • Analog front-end evaluation – FE Modeling – Performance estimation – Architectural comparison 26

Research Proposal (2) • Analog-to-digital encoder and decoder – Modeling ADC as encoder and search process – Optimality of encoding and decoding • Delta-sigma modulator – Decoding algorithm performance – Multidimensional space-time architecture – Stability analysis – Mixed-signal processing schemes 27

Preliminary Research: Analog Front-end Evaluation • Analysis on front-end (FE) of Analog-todigital Converter (ADC) • Function block models • FE Performance evaluation 28

Analysis on Analog FE of ADC • Definitions of analog FE • Problem statement • Proposed FE function blocks 29

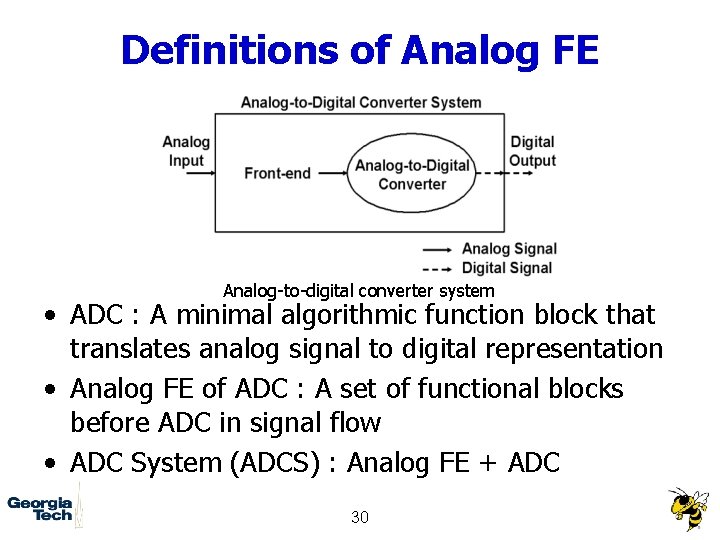
Definitions of Analog FE Analog-to-digital converter system • ADC : A minimal algorithmic function block that translates analog signal to digital representation • Analog FE of ADC : A set of functional blocks before ADC in signal flow • ADC System (ADCS) : Analog FE + ADC 30

Problem Statement • Analog FE – characterizes input signal and noise – limits performance of ADC – has been mixed with ADC – is overlooked in many ADC designs – has been assumed to be good enough without quantitative analysis 31

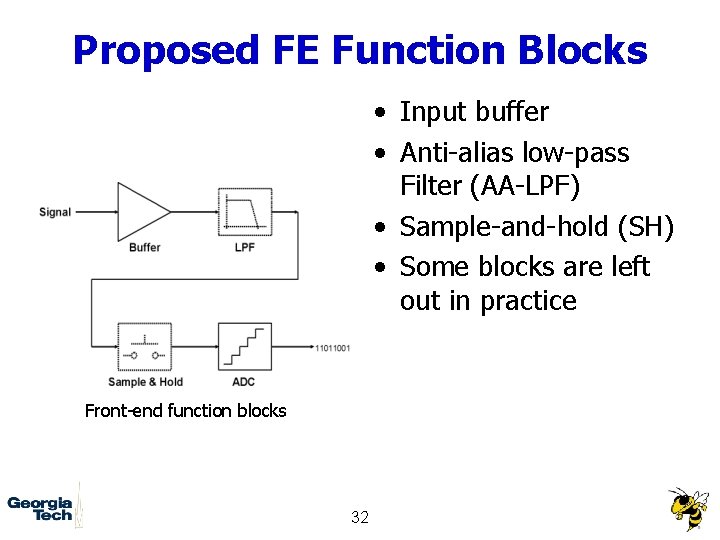
Proposed FE Function Blocks • Input buffer • Anti-alias low-pass Filter (AA-LPF) • Sample-and-hold (SH) • Some blocks are left out in practice Front-end function blocks 32

Function Block Models • • • Input buffer Anti-alias low-pass filter Sample-and-hold Input signal Signal and circuit noise Continuous-time delta-sigma ADC 33

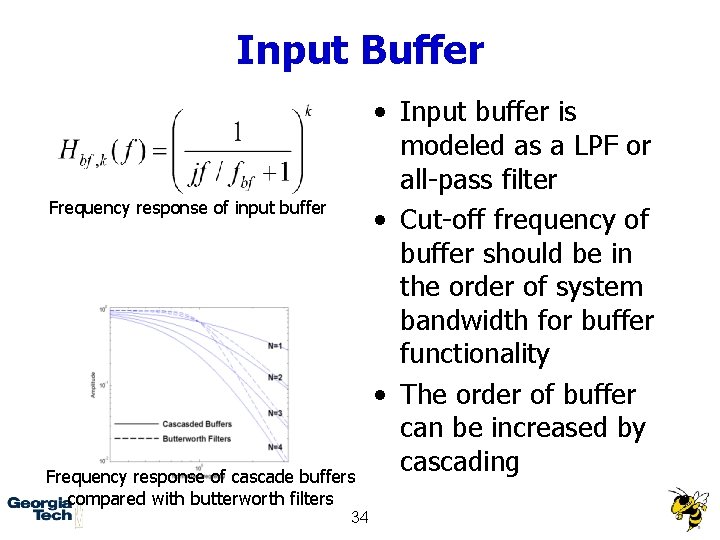
Input Buffer Frequency response of input buffer Frequency response of cascade buffers compared with butterworth filters 34 • Input buffer is modeled as a LPF or all-pass filter • Cut-off frequency of buffer should be in the order of system bandwidth for buffer functionality • The order of buffer can be increased by cascading

Anti-alias Low-pass Filter • Implementation Types – Butterworth – Chebyshev – Elliptic • Butterworth – Minimum pass-band ripples – Less sensitive to filter coefficient error Butterworth filter frequency response • Optimal cut-off frequency for maximum SNR against signal aliasing can be obtained SNR available for filter cut-off frequency 35

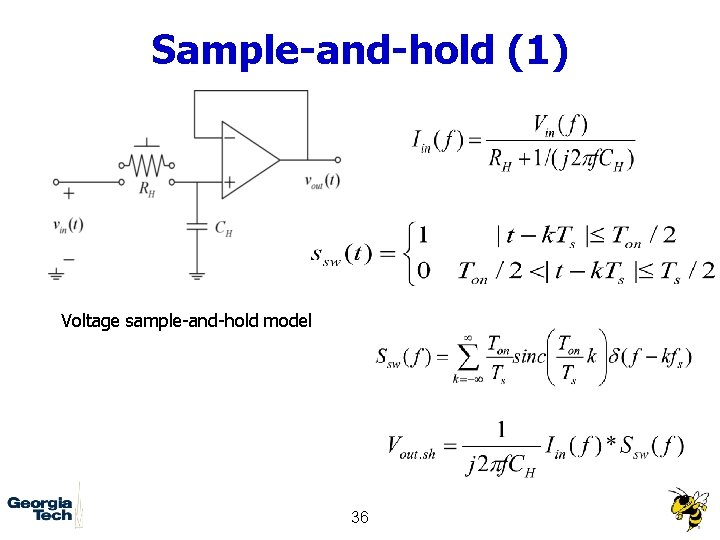
Sample-and-hold (1) Voltage sample-and-hold model 36

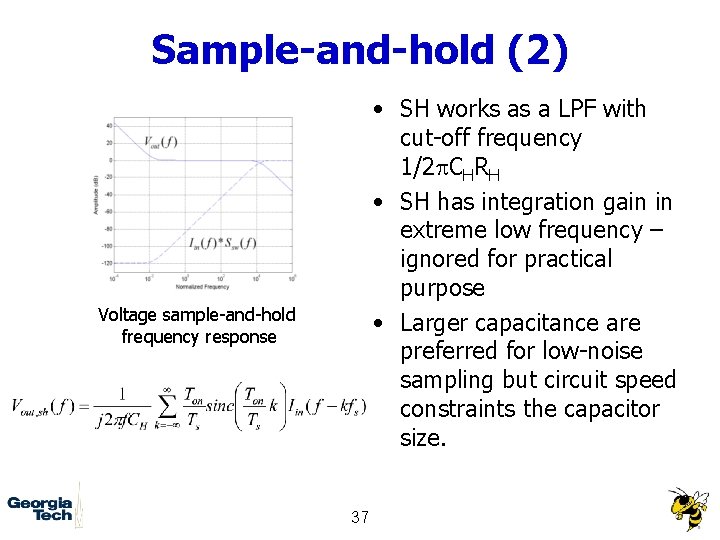
Sample-and-hold (2) • SH works as a LPF with cut-off frequency 1/2 p. CHRH • SH has integration gain in extreme low frequency – ignored for practical purpose • Larger capacitance are preferred for low-noise sampling but circuit speed constraints the capacitor size. Voltage sample-and-hold frequency response 37

Input Signal Model • Model A : Flat • Model B : Bandlimited • Model C : 1 st-order filtered Spectrum of signal models 38

Signal and Circuit Noise • Noise models for signal and circuit: – Flat (Thermal and Shot) noise – Sampling (k. T/C) noise – Signal aliasing • Input signal noise : flat noise with power spectral density (PSD) N 0=1 x 10 -10 • Circuit noise : flat noise with PSD N =1 x 10 t 10 • Sampling noise : k. T/C noise with noise power C=0. 1 n. F, Nc~0. 5 x 10 -10 39

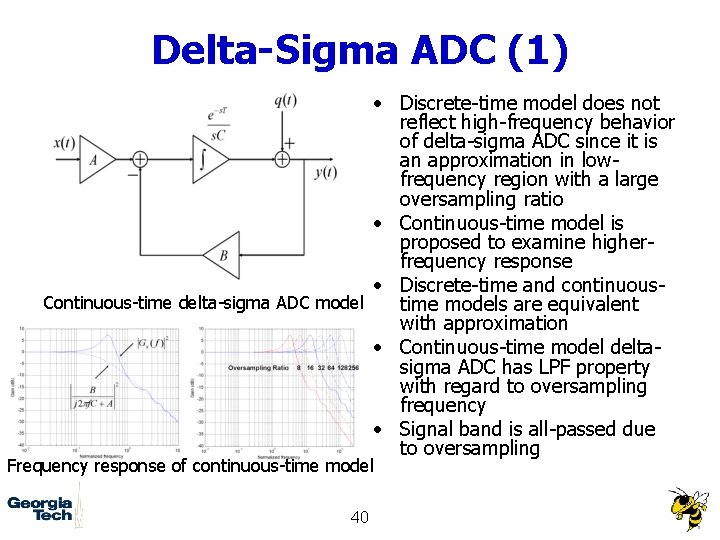
Delta-Sigma ADC (1) • Discrete-time model does not reflect high-frequency behavior of delta-sigma ADC since it is an approximation in lowfrequency region with a large oversampling ratio • Continuous-time model is proposed to examine higherfrequency response • Discrete-time and continuous. Continuous-time delta-sigma ADC model time models are equivalent with approximation • Continuous-time model deltasigma ADC has LPF property with regard to oversampling frequency • Signal band is all-passed due to oversampling Frequency response of continuous-time model 40

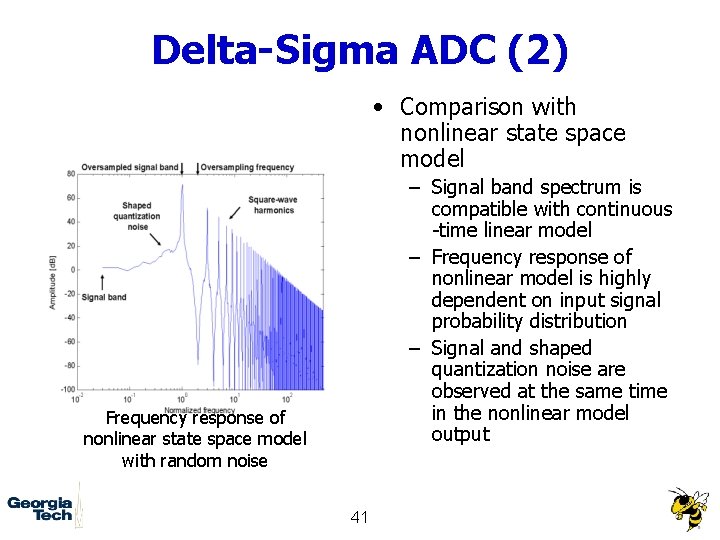
Delta-Sigma ADC (2) • Comparison with nonlinear state space model – Signal band spectrum is compatible with continuous -time linear model – Frequency response of nonlinear model is highly dependent on input signal probability distribution – Signal and shaped quantization noise are observed at the same time in the nonlinear model output Frequency response of nonlinear state space model with random noise 41

FE Performance Evaluation • • • Oversampling assumption Simulation method Traditional FE Direct SH FE without AA-LPF Direct ADC FE without AA-LPF and SH Summary 42

Oversampling Assumption • Input signal is regarded as stationary, quasi-static, or dc when it is oversampled with high oversampling ratio • Attenuation of input signal is enough at Nf. M (half of oversampling frequency) when a simple 1 st-order LPF is used as an AA-LPF for oversampling, and residual signal aliasing is ignorable when it is folded over Nf. M (half of oversampling frequency) • Digital domain multirate signal processing is powerful enough to avoid any signal aliasing during downsampling process • Nominal oversampling ratio is 26 (64) ~ 210 (1024). 43

Simulation Method • Frequency domain computation with cascading of function blocks • Frequency step: 2 x 10 -3 • Frequency range: 2 x 102 • Signal and noise powers are obtained with numerical integration with extended and closed trapezoidal rule • Performance measure: Signal-to-noise ratio (SNR) 44

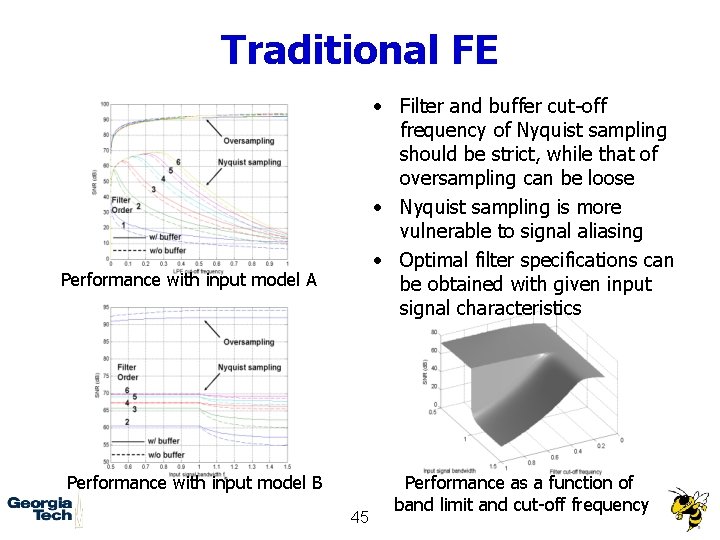
Traditional FE • Filter and buffer cut-off frequency of Nyquist sampling should be strict, while that of oversampling can be loose • Nyquist sampling is more vulnerable to signal aliasing • Optimal filter specifications can be obtained with given input signal characteristics Performance with input model A Performance with input model B 45 Performance as a function of band limit and cut-off frequency

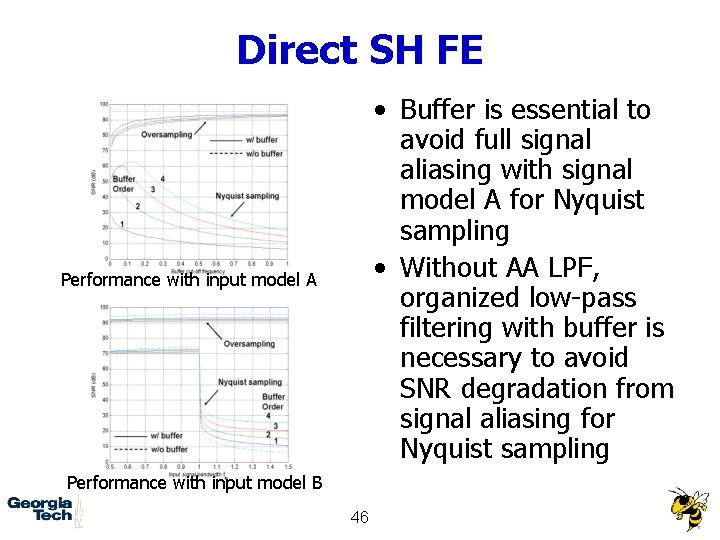
Direct SH FE • Buffer is essential to avoid full signal aliasing with signal model A for Nyquist sampling • Without AA LPF, organized low-pass filtering with buffer is necessary to avoid SNR degradation from signal aliasing for Nyquist sampling Performance with input model A Performance with input model B 46

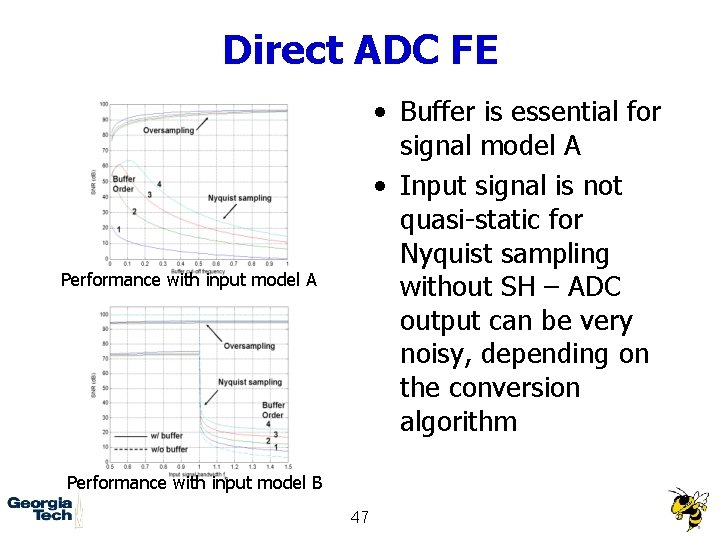
Direct ADC FE • Buffer is essential for signal model A • Input signal is not quasi-static for Nyquist sampling without SH – ADC output can be very noisy, depending on the conversion algorithm Performance with input model A Performance with input model B 47

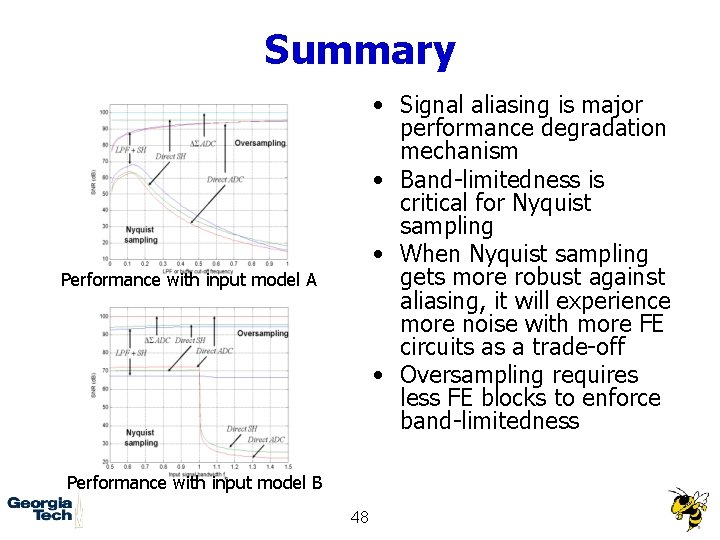
Summary • Signal aliasing is major performance degradation mechanism • Band-limitedness is critical for Nyquist sampling • When Nyquist sampling gets more robust against aliasing, it will experience more noise with more FE circuits as a trade-off • Oversampling requires less FE blocks to enforce band-limitedness Performance with input model A Performance with input model B 48

Future Research • Analog FE Evaluation – Justification of oversampling assumption – Switched-capacitor filter noise modeling • Analog-to-digital encoder and decoder – Modeling ADC as encoder and search process – Optimality of encoding and decoding • Delta-sigma modulator – – Decoding algorithm performance Multidimensional space-time architecture Stability analysis Mixed-signal processing schemes 49

Research Publications • • • M. Thomas, J. Lillie, D. Kim, S. Ralph, N. Jokerst, M. Brooke, K. Dennis, B. Comeau, C. Henderson, "An interferometric sensor for integration with Si CMOS signal processing circuitry: Sensor on a Chip", submitted to CLEO 2004 Daeik D. Kim, Martin A. Brooke, "Modeling and Analysis of High-Pass Delta-Sigma Lock-In Analog-to-Digital Converter, " submitted to ISCAS 2004 Daeik D. Kim, Martin A. Brooke, "Comparison on the Performance of Decoding Schemes for Delta-Sigma Oversampling Converter, " submitted to ISCAS 2004 Daeik D. Kim, Martin A. Brooke, "Architectural Evaluation of Analog-to-Digital Converter Front. End Performance, " submitted to ISCAS 2004 Daeik D. Kim, Mikkel A. Thomas, Martin A. Brooke, Nan M. Jokerst, "Integration of Si-CMOS Embedded Photo Detector Array and Mixed Signal Processing System with Embedded Optical Waveguide Input", under preparation for SPIE Integrated Optoelectronic Devices 2004 Symposium Daeik D. Kim, Martin A. Brooke, "A 1. 4 G Samples/sec Comb Filter Design for Decimation of Sigma-Delta Modulator Output, " Proc. 2003 IEEE ISCAS, pp. 1009 -1012 N. Jokerst, M. A. Brooke, A. S. Brown, S. Y. Cho, R. Huang, S. W. Seo, M. Thomas, I. Song, S. H. Hyun, D. I. Kim, "Optoelectronic Microsystems integration for systems on a package and systems on chip applications, " 2002 OSA Annual Meeting, Tu. V 1, Orlando, Florida, Oct 2002 (Invited) J. Lillie, D. Kim, M. Thomas, M. A. Brooke, N. M. Jokerst, S. E. Ralph, "Highly multimode interferometric sensors, " 2002 OSA Annual Meeting, Tu. L 37, Orlando, Florida, Oct 2002 Sang-Yeon Cho, Mikkel Thomas, Dae-Ik Kim, Nan M. Jokerst, Martin A. Brooke, “Polymer Waveguide Optical Interconnections on Si CMOS Circuits, ” Ctu. F 2, Conference on Lasers and Electro-Optics, Long Beach, CA, p. 161, 2002 50

Conclusion • • Overview Literature review Research proposal Analog FE modeling and performance evaluation as a preliminary research • Future research 51

Questions ? Comments ?

Design of Robust and Flexible On-chip Analog-to-Digital Conversion Architecture Supplemental Slides for Ph. D. Dissertation Proposal Presentation of Daeik Kim Advisor : Prof. Martin Brooke BOSS Team : Dr. N. Jokerst, Dr. S. Ralph Dr. C. Henderson School of Electrical and Computer Engineering Georgia Institute of Technology

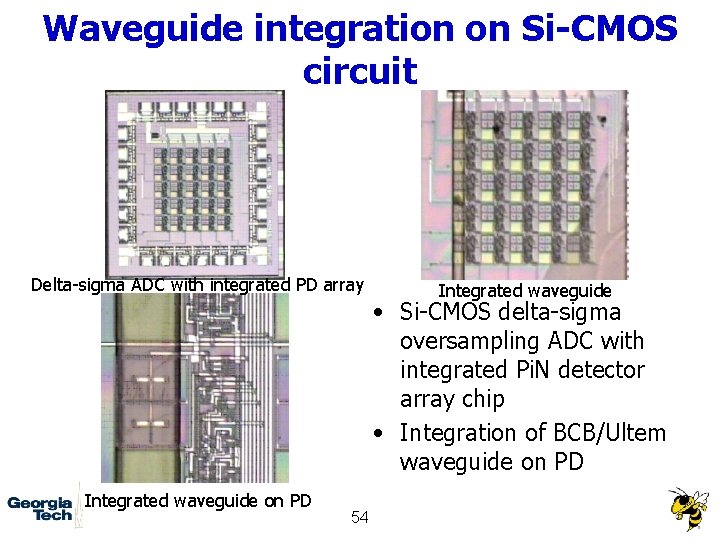
Waveguide integration on Si-CMOS circuit Delta-sigma ADC with integrated PD array Integrated waveguide • Si-CMOS delta-sigma oversampling ADC with integrated Pi. N detector array chip • Integration of BCB/Ultem waveguide on PD Integrated waveguide on PD 54

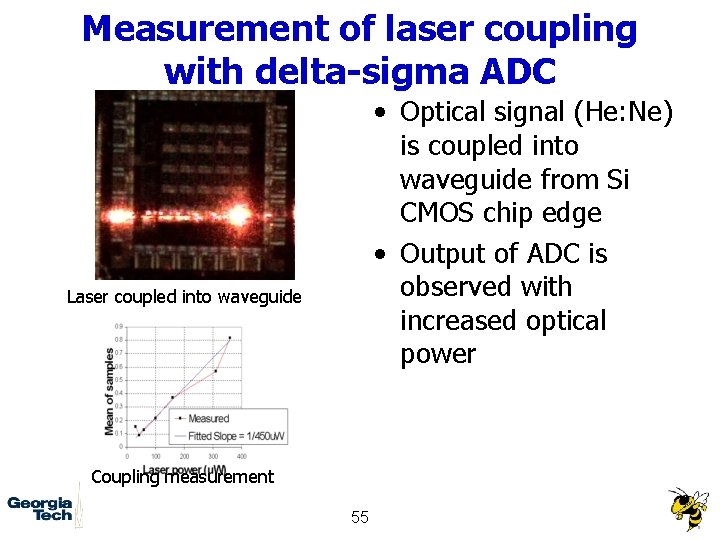
Measurement of laser coupling with delta-sigma ADC • Optical signal (He: Ne) is coupled into waveguide from Si CMOS chip edge • Output of ADC is observed with increased optical power Laser coupled into waveguide Coupling measurement 55

1 -Dimensional Si Photo Detector Array Sensor Chip Si PD + ADC sensor array chip Detector array and front-end • Size: 4. 6 mm by 4. 7 mm • AMI 1. 5 um Si CMOS process • BJT, PN, Pi. N detectors • Delta-sigma oversampling ADC 56

Waveguide Integration on Si. CMOS Circuit Interferometer termination on PD array Interferometer integration Laser coupling into interferometer • Nitride/silicon dioxide Mach Zender interferometers are integrated and tested 57

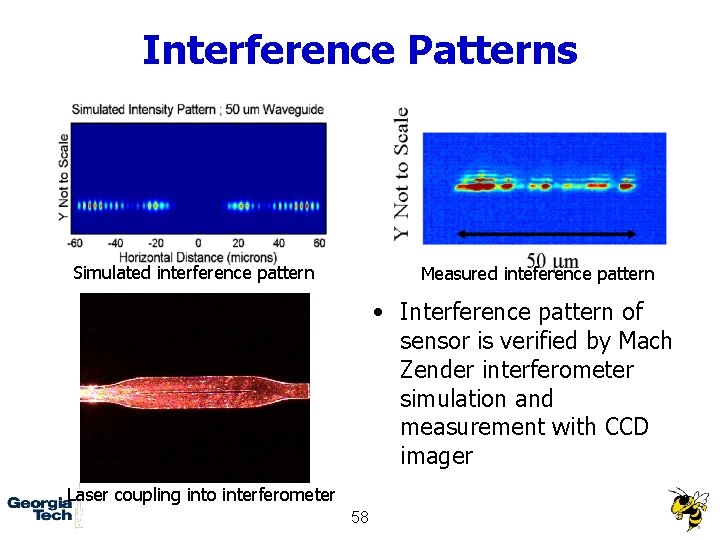
Interference Patterns Simulated interference pattern Measured inteference pattern • Interference pattern of sensor is verified by Mach Zender interferometer simulation and measurement with CCD imager Laser coupling into interferometer 58

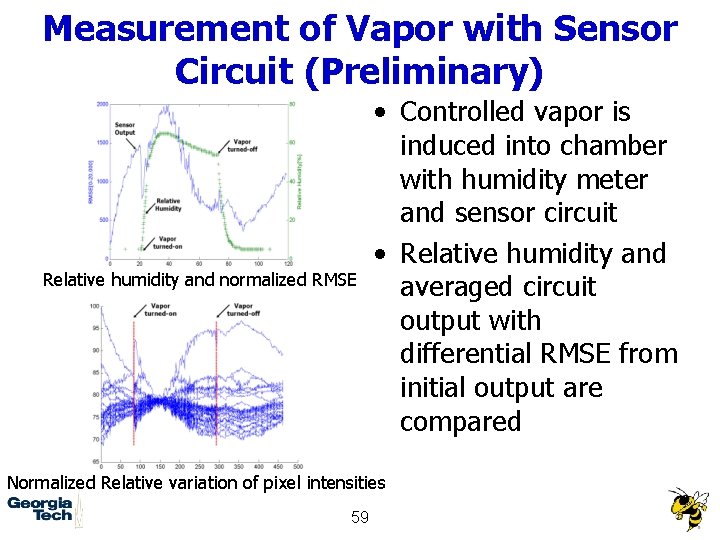
Measurement of Vapor with Sensor Circuit (Preliminary) Relative humidity and normalized RMSE • Controlled vapor is induced into chamber with humidity meter and sensor circuit • Relative humidity and averaged circuit output with differential RMSE from initial output are compared Normalized Relative variation of pixel intensities 59

Work to be done • Minimize side-effects from mechanical movement, light source drift, and chemical reaction of sensor set up • De-correlate side-effects from measurement data • Run sensor test with several active agents • Integrate laser on the chip for a complete system and run sensor tests 60

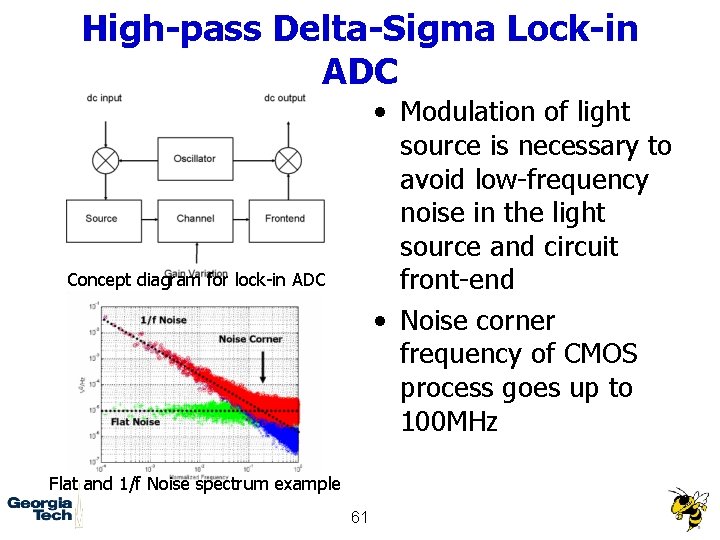
High-pass Delta-Sigma Lock-in ADC • Modulation of light source is necessary to avoid low-frequency noise in the light source and circuit front-end • Noise corner frequency of CMOS process goes up to 100 MHz Concept diagram for lock-in ADC Flat and 1/f Noise spectrum example 61

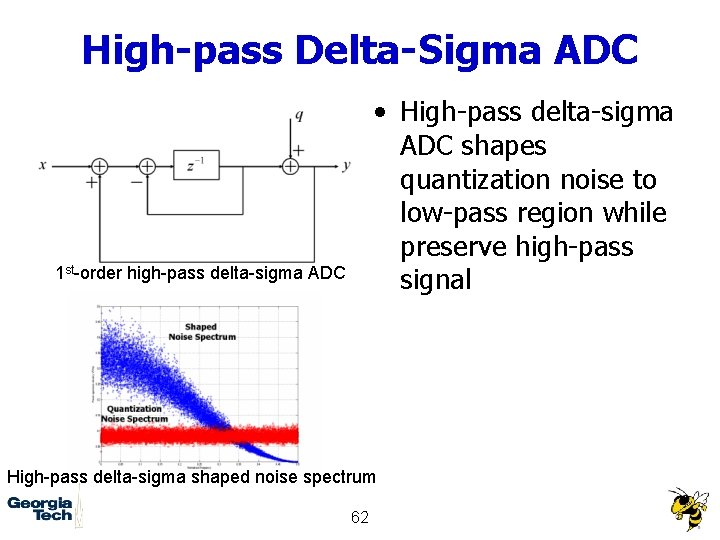
High-pass Delta-Sigma ADC • High-pass delta-sigma ADC shapes quantization noise to low-pass region while preserve high-pass signal 1 st-order high-pass delta-sigma ADC High-pass delta-sigma shaped noise spectrum 62

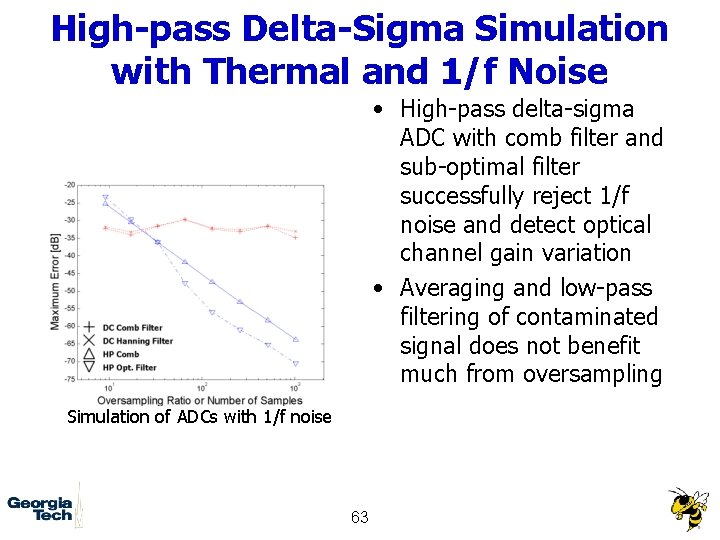
High-pass Delta-Sigma Simulation with Thermal and 1/f Noise • High-pass delta-sigma ADC with comb filter and sub-optimal filter successfully reject 1/f noise and detect optical channel gain variation • Averaging and low-pass filtering of contaminated signal does not benefit much from oversampling Simulation of ADCs with 1/f noise 63

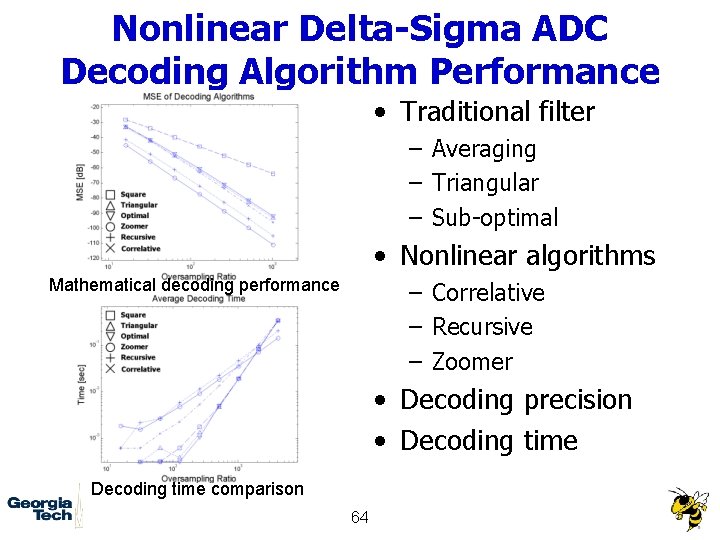
Nonlinear Delta-Sigma ADC Decoding Algorithm Performance • Traditional filter – Averaging – Triangular – Sub-optimal • Nonlinear algorithms Mathematical decoding performance – Correlative – Recursive – Zoomer • Decoding precision • Decoding time comparison 64

Decoding Performance with Circuit Imperfections (1) • Circuit imperfection model – DC offset in initial condition – Leaky integration – Feedback error – Noisy input signal – Noisy quantizer Circuit imperfection model Performance with dc offset in quantizer 65

Decoding Performance with Circuit Imperfections (1) • Circuit imperfection model – DC offset in initial condition – Leaky integration – Feedback error – Noisy input signal – Noisy quantizer Circuit imperfection model Performance with dc offset in quantizer 66

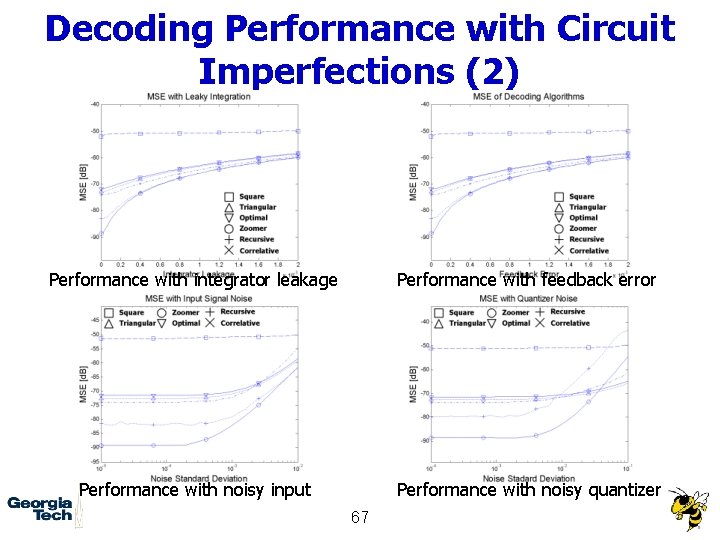
Decoding Performance with Circuit Imperfections (2) Performance with integrator leakage Performance with feedback error Performance with noisy input Performance with noisy quantizer 67