Design of Reinforced Concrete Design of Concrete Beam

Design of Reinforced Concrete

Design of Concrete Beam

Rectangular-section . Design Case 1: Cross section is given Design Case 2: Section dimension are not given 3

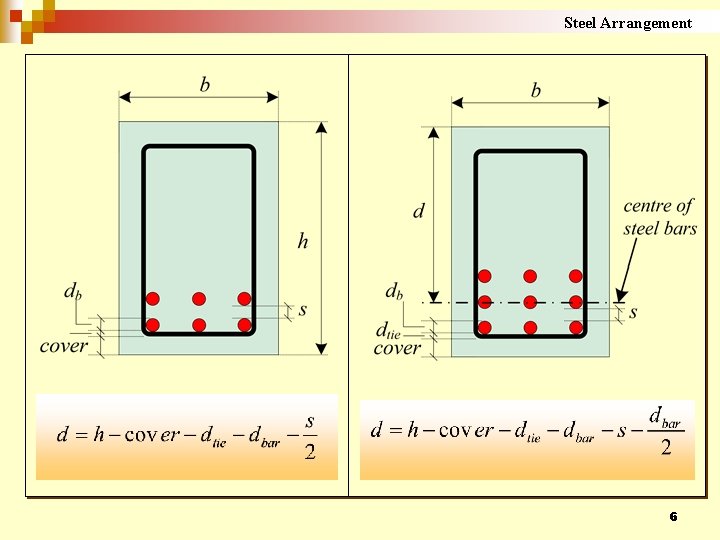
Design case 1: Cross Section is given In this case, the cross dimensions and the material strength (b, h, fcu, fy) are known and it is required to calculate the area of steel reinforcement and its detailing. The design starts with assuming the number of steel layers to calculate d, the effective depth. Table 1 shows different possibilities of steel arrangement in a reinforced concrete section 4

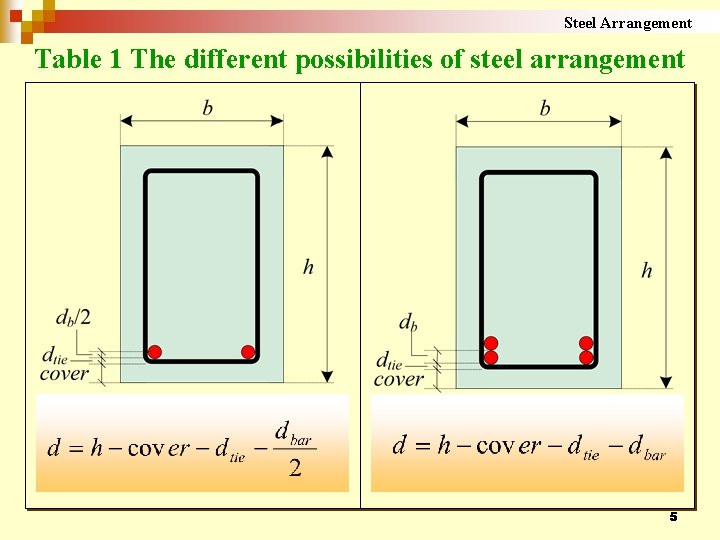
Steel Arrangement Table 1 The different possibilities of steel arrangement 5

Steel Arrangement 6

Rectangular-section After deciding the number of steel layers, the effective depth is calculated as shown in Table (1). However, since the steel amount is not known in the beginning of the design, the designer may assume the number of layer based on his experience and later check the assumption at the end of the design after calculating the steel area. 7

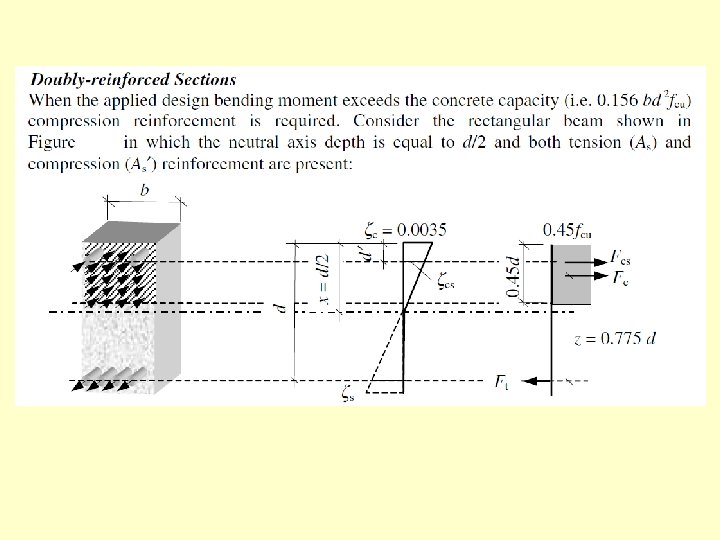
Rectangular-section Next the check whether the section need to be designed as single r. c. section or double r. c section has to be done. To do that the value of “K” need to be calculated as: . § if K 0. 156, the section is designed as singly reinforced concrete section (T. F) § if K > 0. 156 the section is designed as double reinforced concrete section. 8

Rectangular-section In case of K 0. 156, the lever arm z need to be calculated using: ( BS 8110 -clause 3. 4. 4. 4) 9

Rectangular-section The final step in design is to calculate the area of reinforcement necessary to resist the bending moment as: If As < As min use As = As min 10

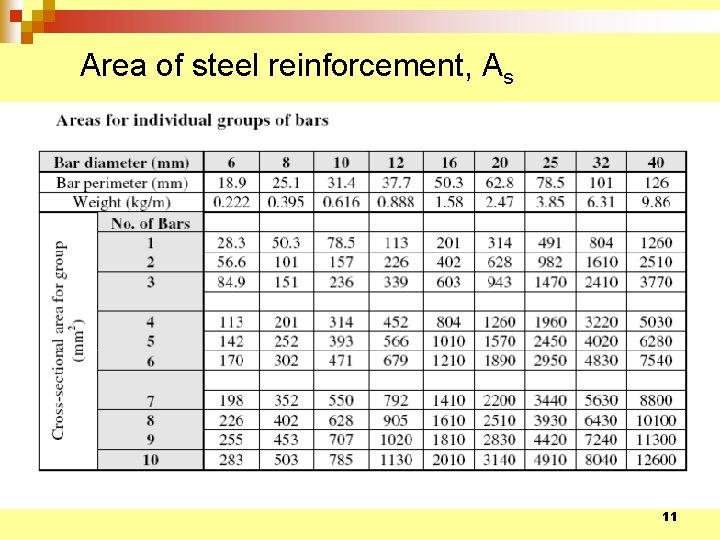
Area of steel reinforcement, As 11

Rectangular-section Design case 2: Section Dimension are not Given • In this case, the width of the beam may be assumed to be similar to the width of columns in the frame or supporting walls. • The design can also starts by assuming b/d (width/effective depth) ratio. As a start b/d may be assumed equal to 0. 5. Again the design must satisfy the ductility requirement (to ensure yielding of steel and hence T. F. ). T. F. Single r. c section Maximum limit axis C. F. Double r. c. section 12

Rectangular-section To identify the depth of the section, design on maximum limit axis by equating the ultimate moment to the Mmax which is the maximum value allowed for a single reinforced section to fail in a ductile manner. The above equation will yields the minimum effective depth required to satisfy ductility requirement as: Lower than this depth with shift the design below the maximum limit axis and the failure will be controlled by compression failure (or steel in compression must be provided). While larger depth will leads to more ductile failure and less steel area. 13

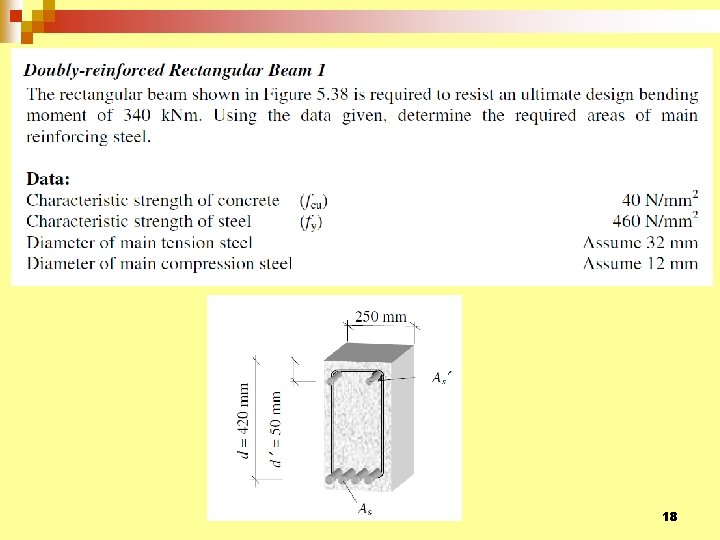
Rectangular-section Example 14

15

17

18

Shear Strength of Sections n The equation in BS 8110 (Cl 3. 4. 5. 2) n Where ¨v = design shear stress ¨ V = design shear force due to ultimate loads ¨ bv=breadth of the section ¨ d =effective depth n v ≤ 0. 8 √(fcu) or ≤ 5 N/mm 2 19

Shear Strength of Sections n n This is the equation given in Table 3. 7 of the code for the cross-sectional area of designed links when the design shear stress v at a crosssection is greater than (vc + 0. 4). It is recognised that the truss analogy produces conservative results and the code specifies that: designed links are required when: (vc + 0. 4) < v < 0. 8 (fcu)1/2 or 5 N/mm 2 20

Shear Strength of Sections n n It is important to provide minimum areas of steel in concrete to minimize thermal and shrinkage cracking, etc. Minimum links are specified in the code which provide a shear resistance of 0. 4 N/mm 2 in addition to the design concrete shear stress vc, and consequently designed links are required when v > (vc + 0. 4) as indicated. In Table 3. 7: minimum links are required when 0. 5 vc < v < (vc + 0. 4) The cross-sectional area of the links required is given by: 21

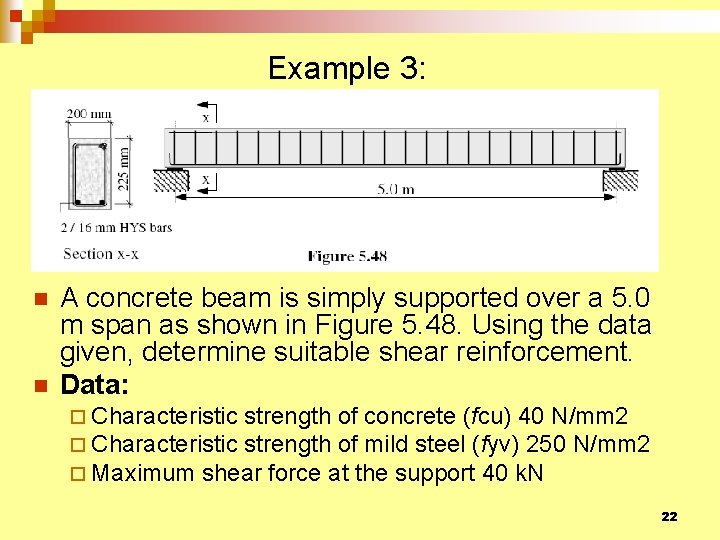
Example 3: n n A concrete beam is simply supported over a 5. 0 m span as shown in Figure 5. 48. Using the data given, determine suitable shear reinforcement. Data: ¨ Characteristic strength of concrete (fcu) 40 N/mm 2 ¨ Characteristic strength of mild steel (fyv) 250 N/mm 2 ¨ Maximum shear force at the support 40 k. N 22

n n n Solution: Consider the end of the beam at the support where the shear force is a maximum = 40 k. N Clause 3. 4. 5. 2 23

n n Table 3. 7 To determine the required reinforcement, evaluate vc and either adopt minimum links throughout or use designed links. As = area of 2/16 mm diameter bars = 402 mm 2 From Table 3. 8 24

n n Since 0. 5 vc < v < (vc + 0. 4), minimum links are required for the whole length of the beam. The cross-sectional area of the links required is given by Option : n Assume 2 -legged / 6 mm diameter mild steel links. ∴Asv = 56. 6 mm 2 n Table 3. 7 The spacing required , n Clause 3. 4. 5. 5 n The maximum spacing of the links ≤ 0. 75 d = (0. 75 x 225) = 169 mm n Adopt 6 mm diameter mild steel links @ 150 mm centres throughout the length of the beam. 25

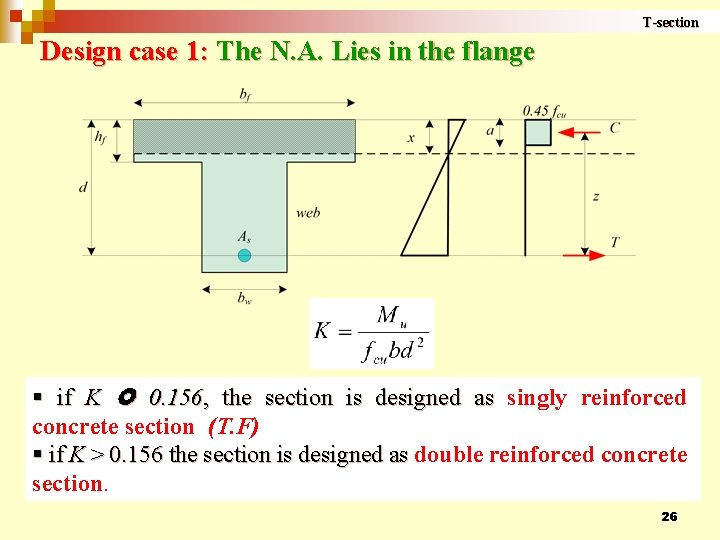
T-section Design case 1: The N. A. Lies in the flange § if K 0. 156, the section is designed as singly reinforced concrete section (T. F) § if K > 0. 156 the section is designed as double reinforced concrete section. 26

T-section In case of K 0. 156, the lever arm z need to be calculated using: then: If As < As min use As = As min 27

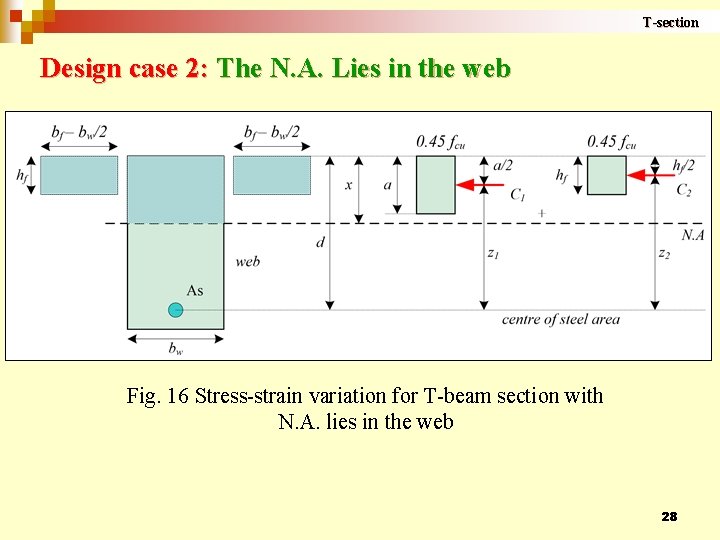
T-section Design case 2: The N. A. Lies in the web Fig. 16 Stress-strain variation for T-beam section with N. A. lies in the web 28

§ to find the location of N. A, we have to check the momnet resistance of the flange: § if Mr > Mu the neutral axis lies in the flange. §if Mr < Mu the neutral axis lies in the web. 29

T-section Simplifying the above equation will yield a 2 nd degree equation in terms of “x” the N. A. depth. If x < xmax = 0. 5 d T. F. the section is designed as single r. c. section If x > xmax = 0. 5 d a compression reinforcement will be required and the section must be designed as double r. c. section. 30

T-section Alternatively, the ultimate may be compared with maximum moment calculated using: § if Mu Mmax it is a T. F and the section is designed as singly reinforced concrete section § if Mu > Mmax it is a C. F and the section is designed as double reinforced concrete section. 31

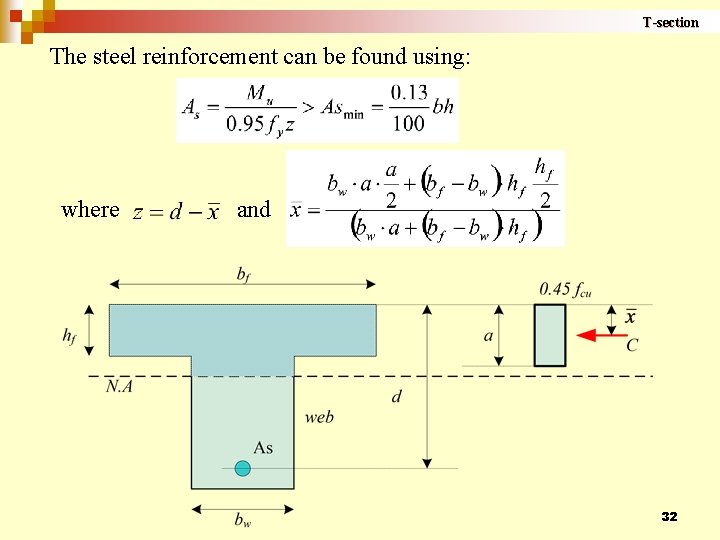
T-section The steel reinforcement can be found using: where and 32

T-section Alternatively, the steel area can be calculated using: 33

T-section Example 1 A simply supported beam having a span of 6 m and carries dead load equal to 14. 8 k. N/m and imposed load of 10 k. N/m. The is monolithically cast with 100 mm thick floor slab. The width of the beam is 250 mm and the architecture fix the total depth to 350 mm. Using fcu = 30 N/mm 2, fy = 460 N/mm 2 find the steel reinforcement at the centre of the beam. 34

T-section Solution 1, cont. Mflange = 0. 45 x 30 x 1450 x 100(304. 5 -100/2)x 10 -6 = 498. 2 k. N. m Mu = 165 < Mflange the N. A. lies in the flange, then: 35

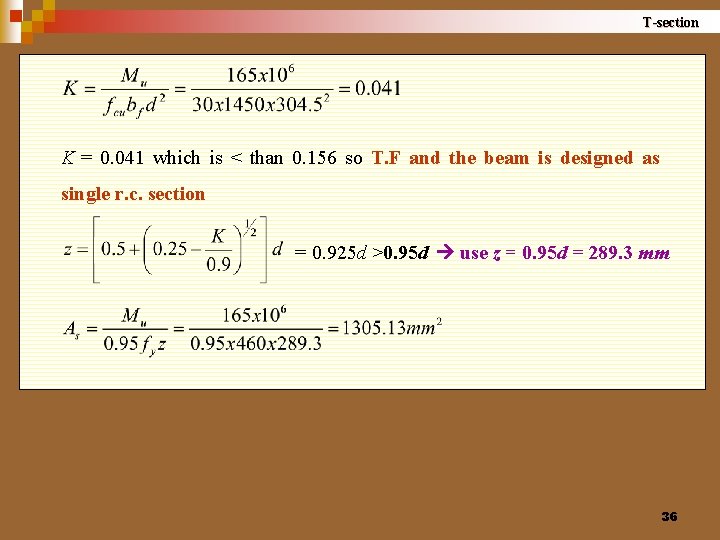
T-section K = 0. 041 which is < than 0. 156 so T. F and the beam is designed as single r. c. section = 0. 925 d >0. 95 d use z = 0. 95 d = 289. 3 mm 36

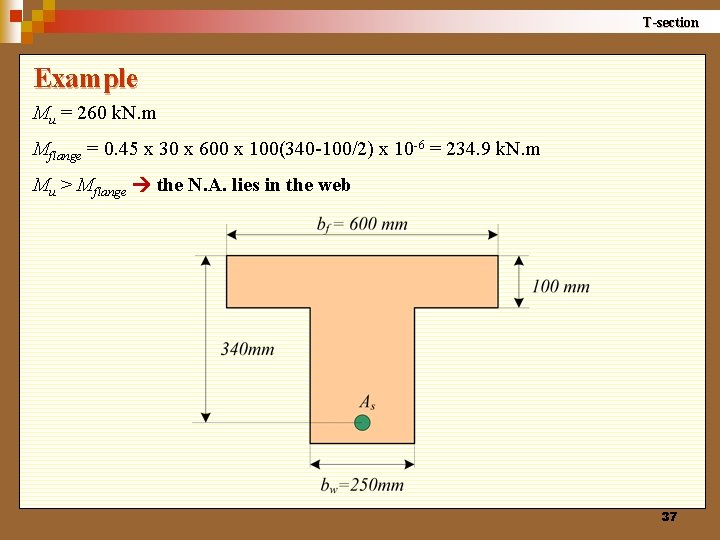
T-section Example Mu = 260 k. N. m Mflange = 0. 45 x 30 x 600 x 100(340 -100/2) x 10 -6 = 234. 9 k. N. m Mu > Mflange the N. A. lies in the web 37

T-section = 0. 156 x 30 x 250 x 3402 +0. 45 x 30(600 -250)100(340 -50)x 10 -6 = 272. 3 k. N. m Mu < Mmax T. F. , the section is considered as single r. c. section use x = 148. 1 mm < 0. 5 d = 170 mm T. F. 2110. 9 mm 2 38