DESIGN OF OPEN WEB GIRDER BRIDGE ATUL KUMAR

DESIGN OF OPEN WEB GIRDER BRIDGE ATUL KUMAR VERMA XEN/SB-I/RDSO

INTRODUCTION ØTruss bridge: § Used for spans greater than what can be spanned economically by a plate girder bridge. § In general truss bridges are used for spans greater than 30 m.

INTRODUCTION Ø Forms Of Open Web Girder Bridges § Through Type § Deck Type (Underslung) § Semi Through Type (Cont. . . )

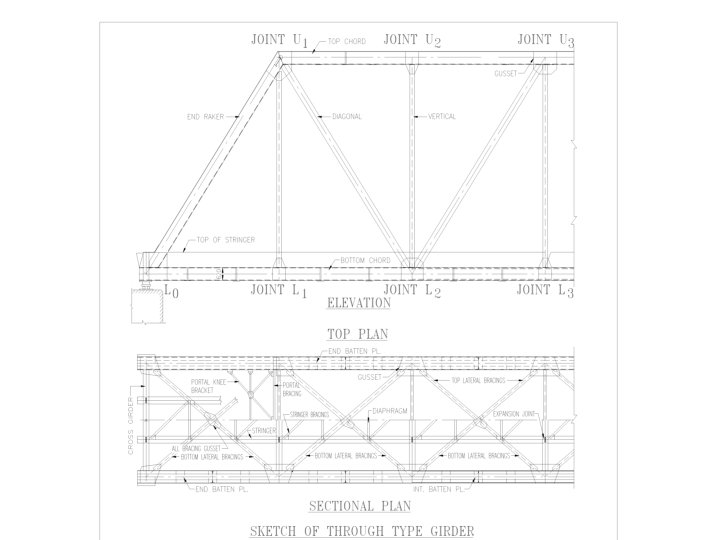
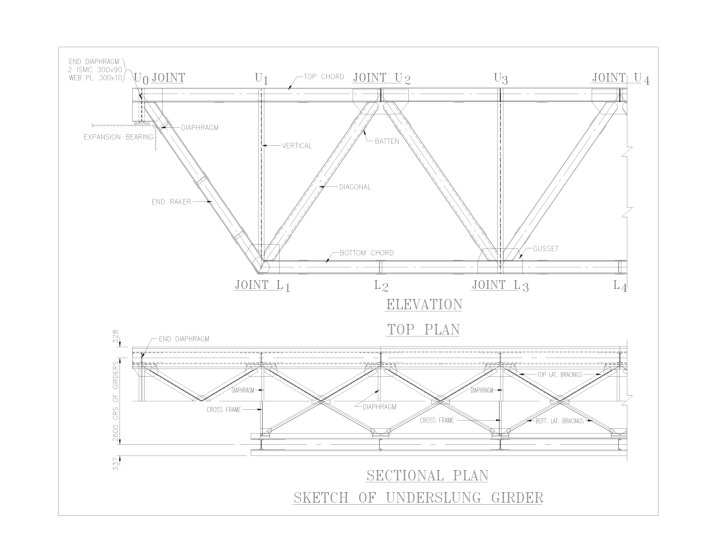
COMPONENTS OF THROUGH TYPE BRIDGE Ø Floor System: § Cross girder (Bending) § Rail bearers or Stringers(Bending) Ø Primary Members: § § § Bottom chord members (Tension members) Top chord members (Compression members) End rackers (Compression & Bending members) Diagonals (Reversible stress members) Verticals (Tension members & redundant members)

COMPONENTS (Cont. . . ) Ø Secondary members: § § § Bottom lateral bracings (Axial force) Top lateral bracings (Axial force) Sway bracings & knee sway (Axial force & Bending) Portal bracings & knee portal (Axial force & Bending) Main gussets Bearings

GENERAL CONFIGRUATION Ø Type of truss § Warren truss with verticals for standard railway spans § Other forms may be adopted as per different conditions Ø Number of panels § Weight of truss Vs Floor system § Optimum number is 6 to 10 Ø Length of panel § Weight of truss Vs Floor system § Optimum length is 6 m. to 9 m. Ø Inclination of diagonals § Between 45° and 60° with the horizontal

GENERAL CONFIGRUATION (Cont…) Ø Height of truss § Through type Vs Deck type § Between 1/8 and 1/5 of span length Ø Spacing of trusses § Sufficient to prevent overturning due to lateral loads § > 1/3 of height of truss & > 1/20 of span

ESTIMATION OF LOADS Ø Dead load Ø Live load Ø Dynamic effects Ø Longitudinal force Ø Racking force Ø Wind pressure effect Ø Forces and effect due to earthquake

DEAD LOAD Ø Dead load of truss is assumed before design on the basis of experience & earlier designs Ø After design of truss the actual dead load of truss is compare with assumed dead load Ø If there is difference between two, then assumed dead load is revised and structure is designed with revised dead load

LIVE LOAD Ø Clause 2. 3 of bridge rule. Ø Estimated on the basis of loading standard. Ø EUDL(equivalent uniformly distributed loads ) are given in appendix of bridge rules for different loading standards. Ø EUDL is given for bending moment and shear force Ø EUDL for Bending Moment: § For Maximum forces in elements resisting bending (Bottom chords & top chords) Ø EUDL for Shear Force: § For Maximum forces in elements resisting shear at section (end racker, diagonals, verticals)

DYNAMIC EFFECTS Ø Clause 2. 4 of bridge rule Ø Augmentation in load due to dynamic effects is considered by adding a load equivalent to a coefficient of dynamic augment(CDA) multiplied by the live load giving the maximum stress in member under consideration. Ø For single track spans: § CDA=0. 15+(8/(6+L)) subject to a maximum of 1. 0 Where L= loaded length of span in meters for the position of the train giving the maximum stress in the member under consideration

LONGITUDINAL FORCES Ø Clause 2. 8 of bridge rule Ø Value of longitudinal force due to either tractive effort or braking force shall be obtained from appendices. Ø Values depend on loaded length and standard of loading. Ø Maximum of tractive effort or braking force is taken as longitudinal force.

RACKING FORCE Ø Clause 2. 9 of bridge rule. Ø Lateral bracings of loaded deck of spans to be designed for a lateral load due to racking force of 600 kg/m. treated as moving load. Ø Racking force not to be considered for calculating stresses in chords or flanges of main girders.

WIND PRESSURE EFFECT Ø Clause 2. 11 of bridge rules. Ø Wind pressure expressed as a equivalent static pressure in windward direction Ø Wind pressure shall apply to all loaded or unloaded bridges. Ø But bridge shall not considered to carry any live load when wind pressure at deck level exceeds 150 kg/m 2 for B. G. Ø Wind force calculated for loaded spans with wind pressure 150 kg/m 2.

WIND PRESSURE EFFECT (Cont…) Ø Wind Force = wind pressure*exposed area Ø Exposed area = area of moving load + exposed area of truss members. Ø Full area of truss members on windward side +50% area of truss members on Leeward side.

SEISMIC FORCE Ø Clause 2. 12 of bridge rule Ø Seismic forces: § Horizontal seismic force § Vertical seismic force Ø Seismic forces calculated taking into consideration seismic zone, importance of structure and its soil foundation system. Ø Design seismic coefficients: α =βIα α = α /2 h v 0 h

SEISMIC FORCE (Cont…) Ø F=Wm*αh (or αv) F = Seismic force Wm=Weight of mass under consideration ignoring reduction due to buoyancy Ø Horizontal seismic force due to live load on the bridge shall be ignored when acting in the direction of traffic Ø When acting in the direction perpendicular to traffic, this is to be considered for 50% of design live load without impact.

ANALYSIS OF FORCES Ø To find out the forces in members of truss due to various loads. Ø Forces can be found out either by suitable computer program or by hand calculation. Ø Hand calculation is done by using influence line diagrams(ILD) for various members of truss. Ø ILD are prepared for a member of truss by calculating force in member as a unit load moves across the deck of the truss. Ø Area of ILD calculated and multiplied by the force intensity to get force in a particular member.

DEAD LOAD ANALYSIS Ø Dead load intensity is same for all the members of truss. Ø Dead load intensity (per truss per unit length) = total assumed dead load/(2*span length) Ø Force due to dead load in each member of truss are calculated by multiplying dead load intensity with area of ILD.

LIVE LOAD ANALYSIS Ø Bottom chord members have tension in ILD. Loaded length is length of span. Ø Top chord members have compression in ILD. Loaded length is length of span. Ø Live load intensity for chord members =EUDL bending/(2*loaded length) Ø CDA for chord members is calculated taking L as span length. Ø End racker have compression in ILD. Loaded length is length of span. Ø Live load intensity for end racker =EUDL shear/(2*loaded length)

LIVE LOAD ANALYSIS (Cont…) Ø CDA for end racker is calculated taking L as span length. Ø Diagonal members have both tension & compression in ILD. loaded length for tension & compression is found from ILD. Ø Live load intensity & CDA for diagonals are calculated for tension & compression both based on their respective loaded lengths. Ø Force due to live load = ILD area*live load intensity Ø Force due to dynamic effect = CDA*force due to live load

LONGITUDINAL FORCE Ø Longitudinal force taken for only bottom chord members. Ø This depends on position of different bottom chord members. Ø For bottom chord member in end panel loaded length for longitudinal force is full span. Ø Loaded length reduces by one panel length as we take bottom chords of other panels starting from end to centre. Ø Based on loaded length longitudinal force is found in bottom chord members.

WIND LOAD ANALYSIS Ø General concept of load transfer and how the wind forces are distributed among the members ØWind Load = Wind pressure X exposed area ØExposed Area = Area of moving load + exposed area of truss member

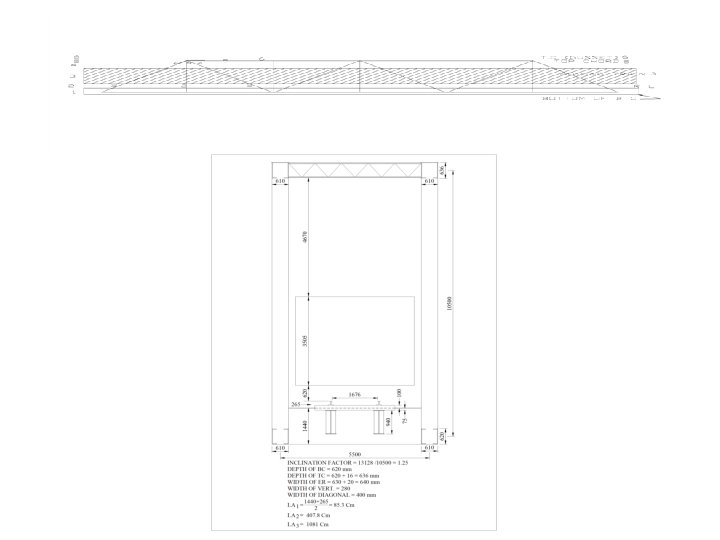
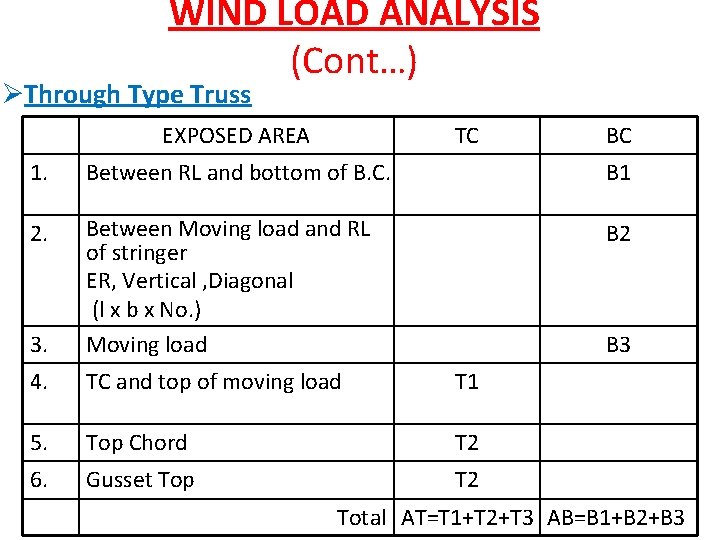
WIND LOAD ANALYSIS (Cont…) ØThrough Type Truss EXPOSED AREA TC BC 1. Between RL and bottom of B. C. B 1 2. B 2 3. Between Moving load and RL of stringer ER, Vertical , Diagonal (l x b x No. ) Moving load 4. TC and top of moving load T 1 5. Top Chord T 2 6. Gusset Top T 2 B 3 Total AT=T 1+T 2+T 3 AB=B 1+B 2+B 3

WIND LOAD ANALYSIS (Cont…) Ø Wind force on top chord = Wind pressurex. ATX 1. 5=WT Ø Wind force on bottom chord= W P[1. 5(ABB 3)+B 3]=WB Ø Nodal force at top chord: § At intermediate nodes = WT/No. of top panel=Tint. § At end nodes = Tint/2 Ø Nodal force at bottom chord: § At intermediate nodes = WB/No. of bottom panel=Bint. § At end nodes = Bint/2

WIND LOAD ANALYSIS (Cont…) Ø Wind load analysis is done for following situations: § Horizontal bending of bottom chord due to wind force on bottom chord & moving load § Vertical bending of span due to wind force on bottom chord & moving load § Horizontal bending of bottom chord due to wind force on top chord transmitted through sway bracings § Vertical bending of span due to wind force on top chord transmitted through sway bracings § Horizontal bending of top chord due to wind load on top chord § Overturning effect of portal

SEISMIC FORCE ANALYSIS Ø Seismic force calculated in horizontal & vertical direction Ø In horizontal direction seismic force calculated for bottom chord & top chord Ø On bottom chord seismic force is due to dead load as well as live load & on top chord seismic force is due to dead load only Ø In vertical direction seismic force is due to dead load as well as live load Ø Analysis of seismic forces in members is same as that of wind force

FORCE IN TRUSS MEMBERS Ø Force in truss members found by adding forces due to dead load, live load with dynamic effect, longitudinal loads, wind load or seismic loads

DESIGN OF STRINGER Ø Loaded length for stringer = length of one panel Ø Bending moment & shear force calculated by getting EUDL bending or EUDL shear as per case Ø Dead load of stringer & track also considered Ø Section assumed for stringer Ø Actual stresses calculated for bending moment & shear force Ø Permissible stresses for bending is minimum of : § Basic permissible stress (clause 3. 7 of SBC) § Permissible stress in fatigue (clause 3. 6 of SBC) § Permissible stress in bending compression (clause 3. 9 of SBC)

DESIGN OF STRINGER (Cont…) Ø Permissible shear stress (Table II of SBC) Ø Actual stress < permissible stress then assumed section is safe otherwise revise the section Ø Design of connection between web & flange of stringer: § Calculation of horizontal shear at the level of weld § Permissible stress in weld (Appendix-G of SBC & clause 13. 4 of welded bridge code) § Size of weld calculated (Subject to clause 6. 2 of welded bridge code)

DESIGN OF STRINGER (Cont…) Ø Provision of stiffeners (Clause 5. 10 of SBC) Ø Design of stringer bracings: § Calculation of lateral load (Clause 2. 9. 2 of bridge rule) § Analysis force in stringer bracings. § Design of stringer bracings (Clause 6. 2. 3 & 3. 8 of SBC)

DESIGN OF CROSS GIRDER Ø Loaded length for cross girder for EUDL = 2*centre to centre distance of cross girder Ø L for CDA = 2. 5*cross girder spacing Ø Bending moment & shear force calculated by getting EUDL Ø Dead load of stringer, track & cross girder also considered Ø Section assumed for cross girder Ø Design process for cross girder is same as stringer

DESIGN OF CROSS GIRDER (Cont…) Ø Connection of cross girder with stringer § Calculate number of rivets for: -one span loaded -both span loaded Ø Connection of cross girder with vertical & Bottom chord § Find rivet value & calculate number of rivets required for connection

DESIGN OF BOTTOM CHORD Ø Bottom chord members are tension member Ø Section assumed for Bottom chord members (Taking into consideration clause 4. 5 & clause 6. 7 of SBC) Ø Effective area of the section calculated (clause 4. 3. 2 of SBC) Ø Actual stresses calculated for axial tension for: § Without longitudinal & seismic or wind forces § With longitudinal & seismic or wind forces Ø Permissible stress for axial tension is minimum of: § Basic permissible stress (clause 3. 7 of SBC) § Permissible stress in fatigue (clause 3. 6 of SBC)

DESIGN OF BOTTOM CHORD (Cont…) Ø Permissible stress for wind or seismic case is increased by 16. 667% (Table 1 of SBC ) Ø Actual stress < permissible stress for both cases then assumed section is safe otherwise revise the section Ø Design of stitching weld: § Calculation of force at the level of weld § Permissible stress in weld ( appendix-G of SBC & clause 13. 4 of welded bridge code) § Size of weld calculated (subject to clause 6. 2 of welded bridge code) Ø Design of lacing & battening of tension members (Clause 6. 9 & 6. 10 of SBC) Ø Design of diaphragms (Clause 6. 16 of SBC)

DESIGN OF TOP CHORD Ø Top chord members are compression member Ø Section assumed for top chord members (taking into consideration clause 4. 5 & clause 6. 2 of SBC) Ø Effective area of the section (clause 6. 2. 2 of SBC) Ø Actual stresses calculated for axial compression for : § Without seismic or wind forces § With seismic or wind forces Ø Permissible stress in axial compression is minimum of: Ø Basic permissible stress (clause 3. 7 of SBC) Ø Stress in axial compression (clause 3. 7 of SBC) Ø Permissible stress in fatigue (clause 3. 6 of SBC)

DESIGN OF TOP CHORD (Cont…) Ø Permissible stress for wind or seismic case is increased by 16. 667% (Table 1 of SBC ) Ø Actual stress < permissible stress for both cases then assumed section is safe otherwise revise the section Ø Design of stitching weld: § Calculation of force at the level of weld § Permissible stress in weld (Appendix-G of SBC & clause 13. 4 of welded bridge code) § Size of weld calculated (Subject to clause 6. 2 of welded bridge code) Ø Design of lacing & battening of compression members (Clause 6. 5 & 6. 6 of SBC) Ø Design of diaphragms (Clause 6. 16 of SBC)

DESIGN OF END RACKER Ø End racker subjected to axial compression & bending (Clause 6. 19 of SBC) Ø Section assumed for end racker (taking into consideration clause 4. 5 & clause 6. 2 of SBC) Ø Effective area of the section (Clause 6. 2. 2 of SBC) Ø Actual stresses calculated for axial compression & bending for : § Without seismic or wind forces § With seismic or wind forces Ø Permissible stress in compression is minimum of: § Basic permissible stress (Clause 3. 7 of SBC) § stress in axial compression (Clause 3. 7 of SBC) § permissible stress in fatigue (Clause 3. 6 of SBC)

DESIGN OF END RACKER (Cont…) Ø Permissible stress in bending (Table 2 of SBC) Ø Permissible stress for wind or seismic case is increased by 16. 667% for axial compression & bending both (Table 1 of SBC ) Ø Adequacy of section is checked for combined stresses for both cases (Clause 3. 11. 1 of SBC ) Ø Design of stitching weld, design of lacing & battening and design of diaphragms same as compression member

DESIGN OF DIAGONALS & VERTICALS Ø Diagonals are reversible stress members Ø Section of diagonals have to be checked for both tension & compression Ø Verticals are tension members Ø Design done similar to bottom chord

DESIGN OF PORTAL BRACINGS SYSTEM Ø Force analysis in members of portal system done forces: (Clause 6. 19 of SBC) § 50% of lateral forces on top chord § Lateral shear equal to 1. 25% of total force in two end racker or in two top chords in end panel whichever is greater Ø Top member of portal subjected to axial compression & bending moment both Ø Design of top member is similar to that of end racker Ø Knee portal is tension or compression member as per the direction of application of nodal force Ø Knee portal is designed for both axial tension & compression

DESIGN OF TOP LATERAL BRACINGS Ø Force analysis in top lateral bracing system done forces: (Clause 6. 17 of SBC) Ø Lateral force on top chord Ø 2. 5% of force in top chord members Ø Bracing members are tension or compression member depending upon the direction of application of nodal force Ø Bracing members are designed for both axial tension & compression

DESIGN OF BOTTOM LATERAL BRACINGS Ø Force analysis in bottom lateral bracing system done forces: (Clause 6. 17 of SBC) § Lateral force on bottom chord & moving load § 50% of lateral force in top chord transmitted through sway bracings § Racking force § Longitudinal force Ø Bracing members are tension or compression member depending upon the direction of application of nodal force Ø Bracing members are designed for both axial tension & compression

DESIGN OF JOINTS Ø Connection at intersection is done as per clause 6. 12 of SBC Ø Rivet value is calculated for rivets to be used Ø Number of rivets = force in member/rivet value Ø Arrangement of rivets at a joint is done as per clause 7. 1 to 7. 9 of SBC Ø Splicing of members is done as per clause 6. 11 of SBC

CAMBER Ø Camber diagram is prepared as per clause 4. 16 & appendix-A of SBC Ø Camber calculated for dead load & full live load including impact Ø Forces in members are calculated for these loads Ø Change in length of members due to forces in members = FL/AE Ø In tension members increase in length & for compression members decrease in length Ø Strain correction is applied in nominal length equal to change in length of members Ø For tension members it is negative & for compression members it is positive

CAMBER (Cont…) Ø To avoid changes in the length of floor system further change in length done in length of all members Ø This change equal to ((loaded chord extension or contraction/loaded chord length)*length of member) Ø For through spans this change is increase in length of members & for deck type it will be decrease Ø Nominal lengths altered as above give a girder correctly stressed camber Ø Nominal lengths and cambered length rounded off to nearest 0. 5 mm.

DEFLECTION Ø Deflection < length of girder/600 (Clause 4. 17 of SBC) Ø Vertical deflection at the centre of span is calculated by applying unit load at the centre of truss Ø Deflection at centre=∑((FL/AE)*U)

THANK YOU