Design of Experiments Methods and Case Studies Dan

Design of Experiments – Methods and Case Studies • • Dan Rand Winona State University ASQ Fellow 5 -time chair of the La Crosse / Winona Section of ASQ • (Long) Past member of the ASQ Hiawatha Section

Design of Experiments – Methods and Case Studies • Tonight’s agenda – – The basics of Do. E Principles of really efficient experiments Really important practices in effective experiments Basic principles of analysis and execution in a catapult experiment – Case studies – in a wide variety of applications – Optimization with more than one response variable – If Baseball was invented using Do. E

Design of Experiments - Definition • implementation of the scientific method. -design the collection of information about a phenomenon or process, analyze information, learn about relationships of important variables. - enables prediction of response variables. - economy and efficiency of data collection minimize usage of resources.

Advantages of Do. E • Process Optimization and Problem Solving with Least Resources for Most Information. • Allows Decision Making with Defined Risks. • Customer Requirements --> Process Specifications by Characterizing Relationships • Determine effects of variables, interactions, and a math model • DOE Is a Prevention Tool for Huge Leverage Early in Design

Steps to a Good Experiment • 1. Define the objective of the experiment. • 2. Choose the right people for the team. • 3. Identify prior knowledge, then important factors and responses to be studied. • 4. Determine the measurement system

Steps to a Good Experiment • 5. Design the matrix and data collection responsibilities for the experiment. • 6. Conduct the experiment. • 7. Analyze experiment results and draw conclusions. • 8. Verify the findings. • 9. Report and implement the results

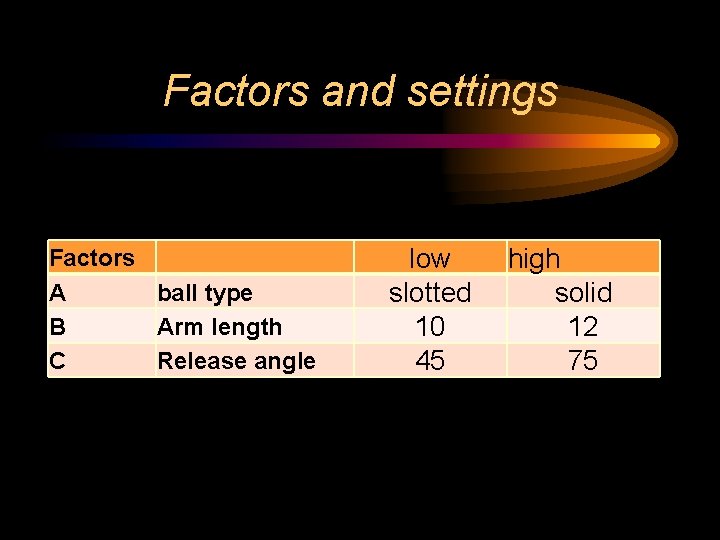
An experiment using a catapult • We wish to characterize the control factors for a catapult • We have determined three potential factors: 1. Ball type 2. Arm length 3. Release angle

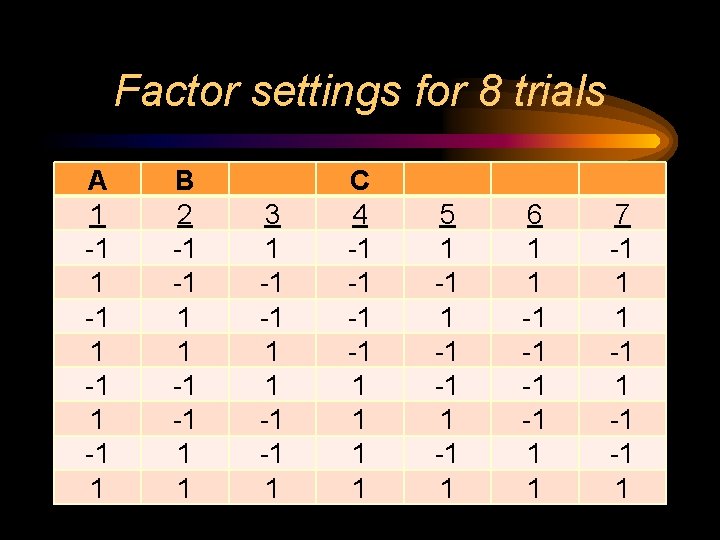
One Factor-at-a-Time Method • Hypothesis test - T-test to determine the effect of each factor separately. • test each factor at 2 levels. Plan 4 trials each at high and low levels of 3 factors • 8 trials for 3 factors = 24 trials. • levels of other 2 factors? • Combine factor settings in only 8 total trials.

Factors and settings Factors A ball type B Arm length C Release angle low slotted 10 45 high solid 12 75

Factor settings for 8 trials A 1 -1 1 B 2 -1 -1 1 1 3 1 -1 -1 1 C 4 -1 -1 1 1 5 1 -1 -1 1 6 1 1 -1 -1 1 1 7 -1 1 1 -1 -1 1

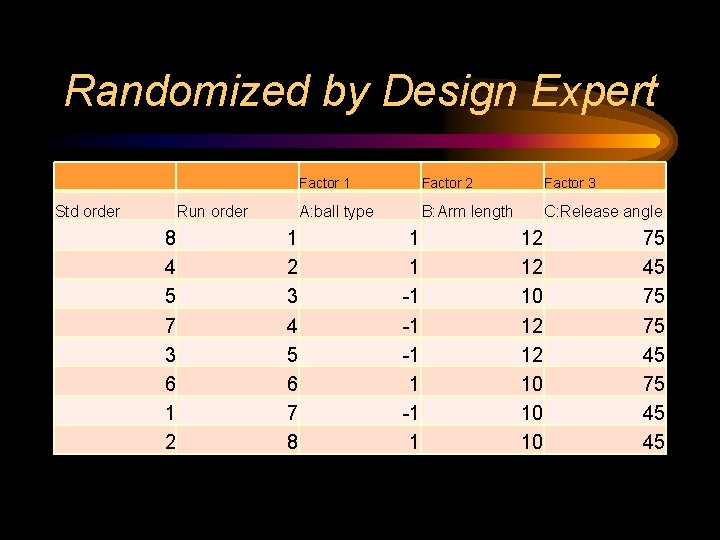
Randomization • The most important principle in designing experiments is to randomize selection of experimental units and order of trials. • This averages out the effect of unknown differences in the population, and the effect of environmental variables that change over time, outside of our control.

From Design Expert:

Randomized by Design Expert Std order Run order 8 4 5 7 3 6 1 2 3 4 5 6 7 8 Factor 1 Factor 2 Factor 3 A: ball type B: Arm length C: Release angle 1 1 -1 -1 -1 1 12 12 10 10 10 75 45 45

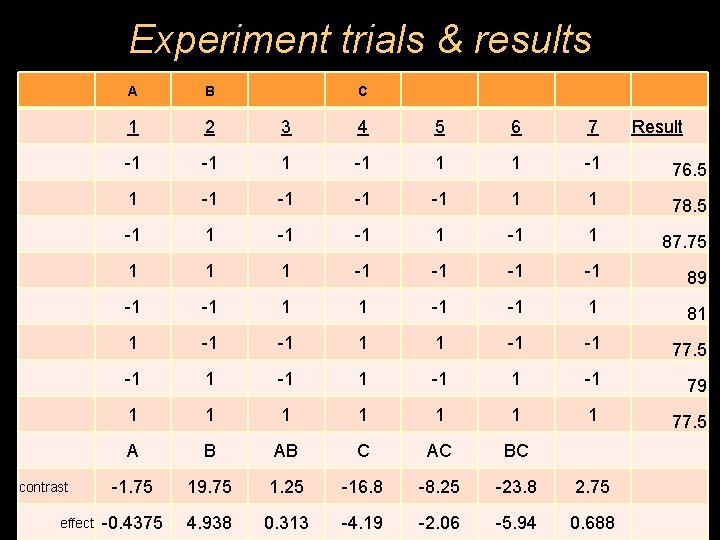
Experiment trials & results contrast effect A B C 1 2 3 4 5 6 7 -1 -1 1 1 -1 76. 5 1 -1 -1 1 1 78. 5 -1 1 87. 75 1 1 1 -1 -1 89 -1 -1 1 1 -1 -1 1 81 1 -1 -1 77. 5 -1 1 -1 79 1 1 1 1 77. 5 A B AB C AC BC -1. 75 19. 75 1. 25 -16. 8 -8. 25 -23. 8 2. 75 -0. 4375 4. 938 0. 313 -4. 19 -2. 06 -5. 94 0. 688 Result

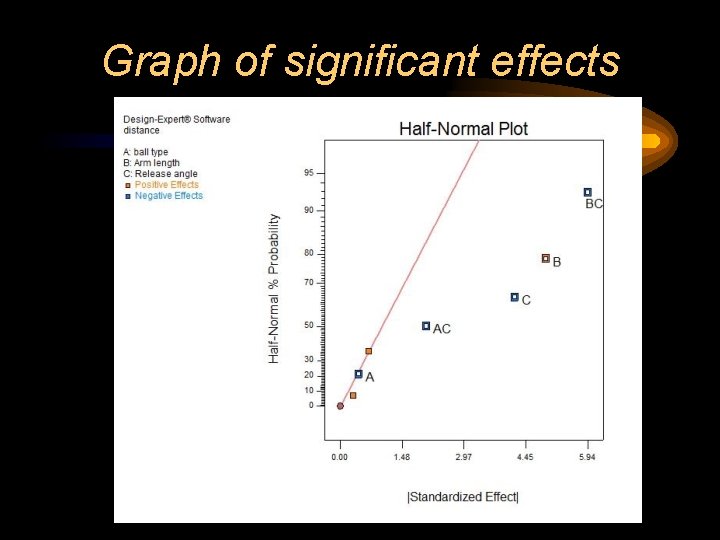
Graph of significant effects

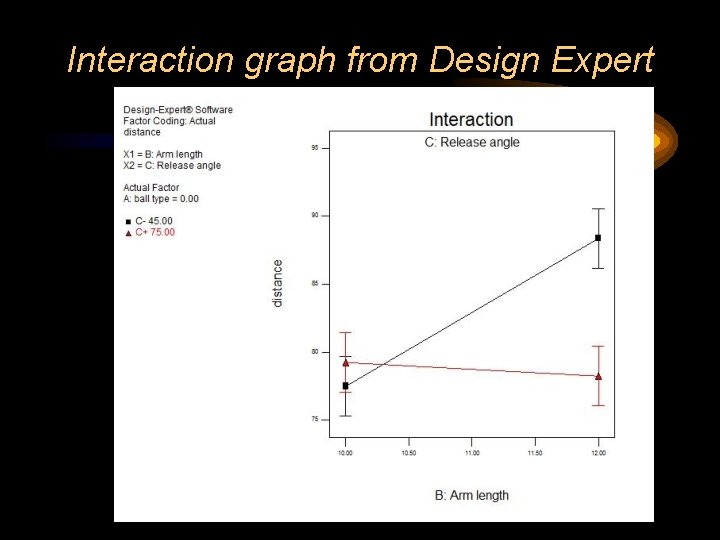
Detecting interactions between factors • Two factors show an interaction in their effect on a response variable when the effect of one factor on the response depends on the level of another factor.

Interaction graph from Design Expert

Predicted distance based on calculated effects • Distance = 80. 84 + 4. 94 * X 2_arm_length – 4. 19* X 3_Release_angle – 2. 06* X 1*X 3 - 5. 94*X 2*X 3 • X 2 = -1 at arm length of 10, = 1 at arm length of 12 • X 3 = -1 at release angle of 45, = 1 at release angle of 75

Poorly executed experiments • If we are sloppy with control of factor levels or lazy with randomization, special causes invade the experiment and the error term can get unacceptably large. As a result, significant effects of factors don’t appear to be so significant.

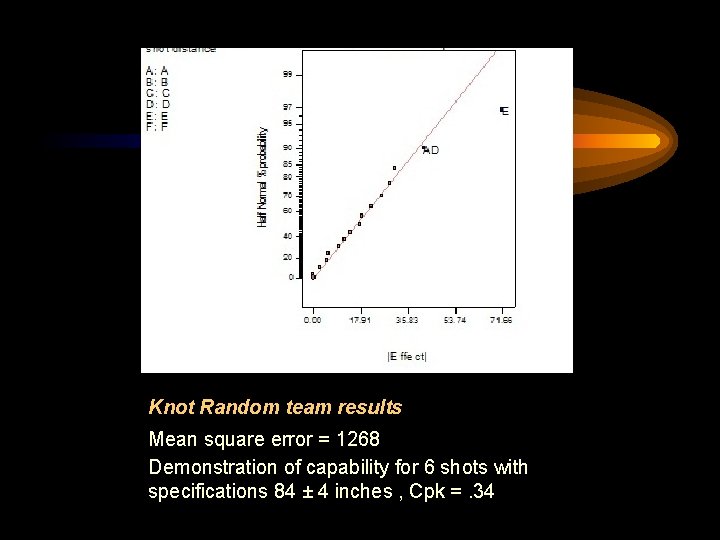
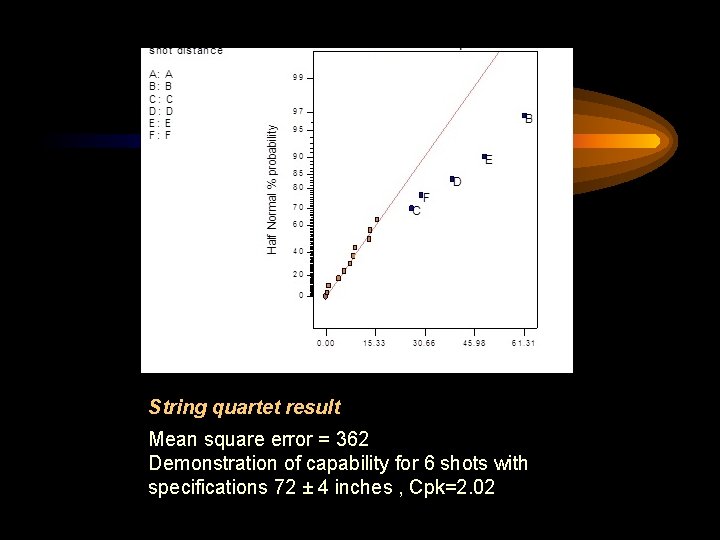
The Best and the Worst • Knot Random Team and the String Quartet Team. Each team designed a 16 -trial, highly efficient experiment with two levels for each factor to characterize their catapult’s capability and control factors.

Knot Random team results Mean square error = 1268 Demonstration of capability for 6 shots with specifications 84 ± 4 inches , Cpk =. 34

String quartet result Mean square error = 362 Demonstration of capability for 6 shots with specifications 72 ± 4 inches , Cpk=2. 02

String Quartet Best Practices • Randomized trials done in prescribed order • Factor settings checked on all trials • Agreed to a specific process for releasing the catapult arm • Landing point of the ball made a mark that could be measured to ¼ inch • Catapult controls that were not varied as factors were measured frequently

Knot Random – Knot best practices • Trials done in convenient order to hurry through apparatus changes • Factor settings left to wrong level from previous trial in at least one instance • Each operator did his/her best to release the catapult arm in a repeatable fashion • Inspector made a visual estimate of where ball had landed, measured to nearest ½ inch • Catapult controls that were not varied as factors were ignored after initial process set-up

Multivariable testing (MVT) as Do. E • “Shelf Smarts, ” Forbes, 5/12/03 • Do. E didn’t quite save Circuit City • 15 factors culled from 3000 employee suggestions • Tested in 16 trials, 16 stores • Measured response = store revenue • Implemented changes led to 3% sales rise

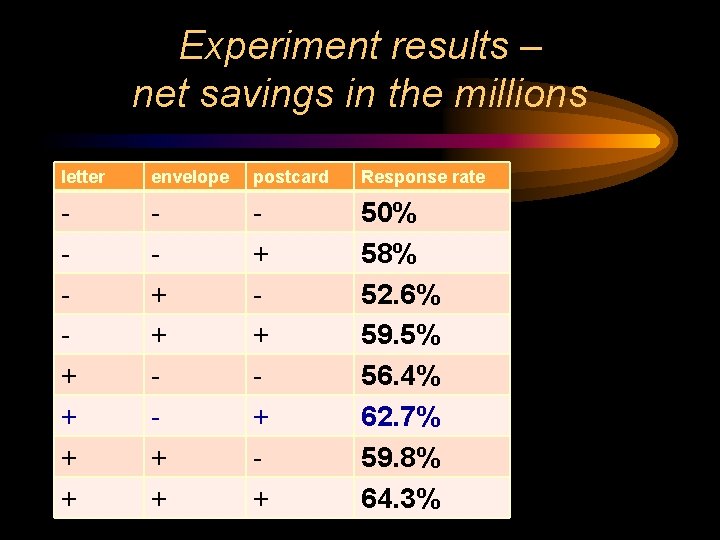
Census Bureau Experiment • “Why do they send me a card telling me they’re going to send me a census form? ? ? ” • Dillman, D. A. , Clark, J. R. , Sinclair, M. D. (1995) “How pre-notice letters, stamped return envelopes and reminder postcards affect mail-back response rates for census questionnaires, ” Survey Methodology, 21, 159 -165

1992 Census Implementation Test • Factors: – Pre-notice letter – yes/ no – SASE with census form – yes / no – Reminder postcard a few days after census form – yes / no – Response = completed, mailed survey response rate

Experiment results – net savings in the millions letter envelope postcard Response rate + + + 50% 58% 52. 6% 59. 5% 56. 4% 62. 7% 59. 8% 64. 3%

Surface Mount Technology (SMT) experiment - problem solving in a manufacturing environment • 2 types of defects, probably related – Solder balls – Solder-on-gold • Statistician invited in for a “quick fix” experiment • High volume memory card product • Courtesy of Lally Marwah, Toronto, Canada

Problem in screening / reflow operations Prep card Solder paste screening Solder paste reflow Clean card insert Inspect (T 1) Component placement Inspect (T 2)

8 potential process factors • • Clean stencil frequency: 1/1, 1/10 Panel washed: no, yes Misregistration: 0, 10 ml Paste height: 9 ml, 12 ml Time between screen/ reflow: . 5, 4 hr Reflow card spacing: 18 in, 36 in Reflow pre-heat: cold, hot Oven: A, B

Experiment design conditions • • Resources only permit 16 trials Get efficiency from 2 -level factors Measure both types of defects Introduce T 1 inspection station for counting defects • Same inspectors • Same quantity of cards per trial

Can we measure effects of 8 factors in 16 trials? Yes

7 more columns contain all interactions • Each column contains confounded interactions

Normal plot for factor effects on solder ball defects C CD D

Which confounded interaction is significant? • AF, BE, CD, or GH ? • The main effects C and D are significant, so engineering judgement tells us CD is the true significant interaction. • C is misregistration • D is paste height

Conclusions from experiment • Increased paste height (D+) acts together with misregistration to increase the area of paste outside of the pad, leading to solder balls of dislodged extra paste. • Solder ball occurrence can be reduced by minimizing the surface area and mass of paste outside the pad.

Implemented solutions • Reduce variability and increase accuracy in registration. • Lowered solder ball rate by 77% • More complete solution: • Shrink paste stencil opening - pad accommodates variability in registration.

The Power of Efficient Experiments • More information from less resources • Thought process of experiment design brings out: – potential factors – relevant measurements – attention to variability – discipline to experiment trials

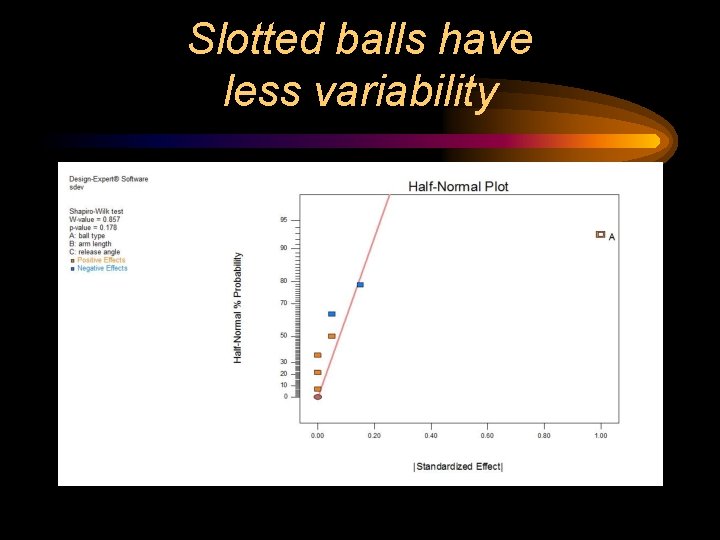
Optimization – Back to the Catapult • • Optimize two responses for catapult Hit a target distance Minimize variability Suppose the 8 trials in the catapult experiment were each run with 3 replicates, and we used means and standard deviations of the 3

8 catapult runs with response = standard deviation (sdev) A B C sdev -1 -1 -1 1. 6 1 -1 -1 2. 5 -1 1. 5 1 1 -1 2. 6 -1 -1 1 1. 4 1 -1 1 2. 4 -1 1 1 1. 4 1 1 1 2. 4

Slotted balls have less variability

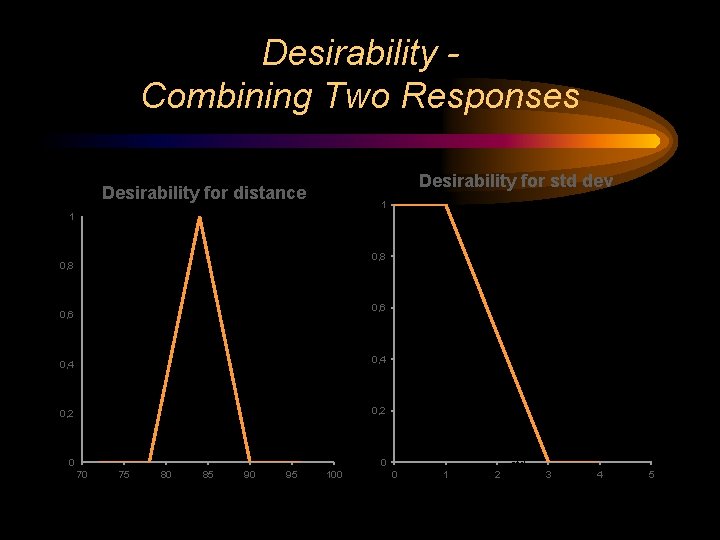
Desirability Combining Two Responses Desirability for std dev Desirability for distance 1 1 0, 8 0, 6 d 0, 4 0, 2 0 0 70 75 80 85 90 95 100 0 1 2 std 3 4 5

Maximum Desirability • Modeled response equation allows hitting the target distance of 84, d=1 • Best possible standard deviation according to model is 1. 475 • d (for std dev) = (3 -1. 475)/(3 -1) =. 7625 • D = SQRT(1*. 7625) =. 873

How about a little baseball? • • Questions? Thank you E-mail me at drand@winona. edu Find my slides at http: //course 1. winona. edu/drand/web/