Design of Engineering Experiments Part 8 Overview of

Design of Engineering Experiments Part 8 – Overview of Response Surface Methods • Text reference, Chapter 11, Sections 11 -1 through 11 -4 • Primary focus of previous chapters is factor screening – Two-level factorials, fractional factorials are widely used • Objective of RSM is optimization • RSM dates from the 1950 s; early applications in chemical industry DOX 6 E Montgomery 1

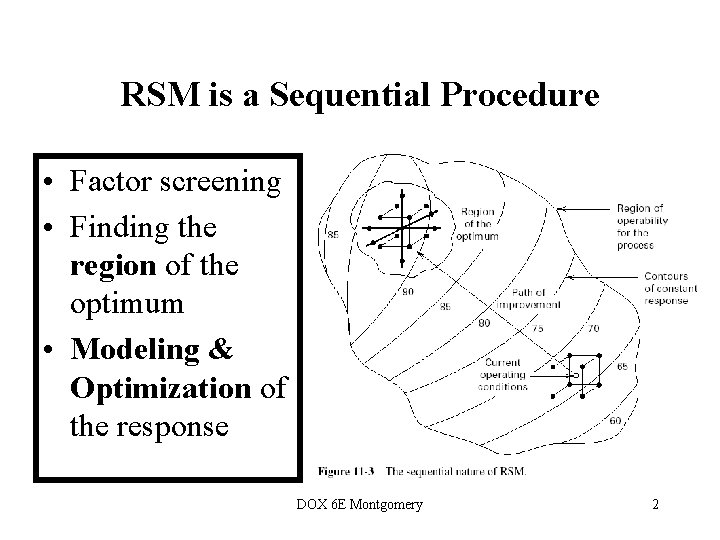
RSM is a Sequential Procedure • Factor screening • Finding the region of the optimum • Modeling & Optimization of the response DOX 6 E Montgomery 2

Response Surface Models • Screening • Steepest ascent • Optimization DOX 6 E Montgomery 3

The Method of Steepest Ascent Text, page 407 A procedure for moving sequentially from an initial “guess” towards to region of the optimum Based on the fitted first-order model Steepest ascent is a gradient procedure DOX 6 E Montgomery 4

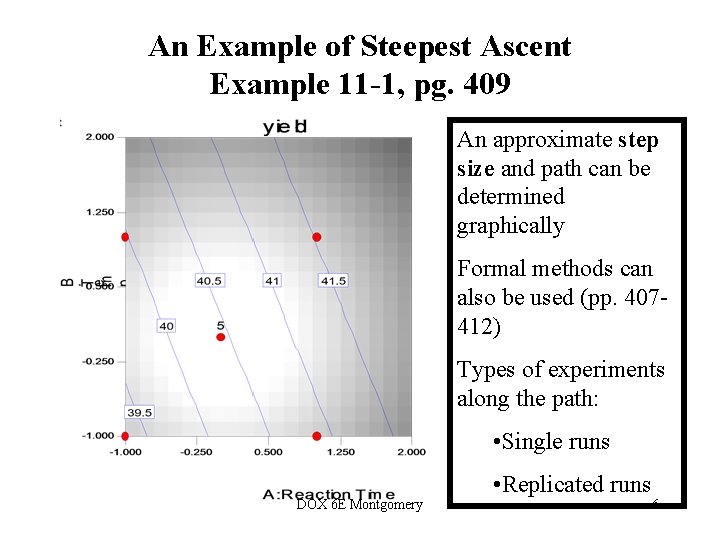
An Example of Steepest Ascent Example 11 -1, pg. 409 DOX 6 E Montgomery 5

An Example of Steepest Ascent Example 11 -1, pg. 409 An approximate step size and path can be determined graphically Formal methods can also be used (pp. 407412) Types of experiments along the path: • Single runs DOX 6 E Montgomery • Replicated runs 6

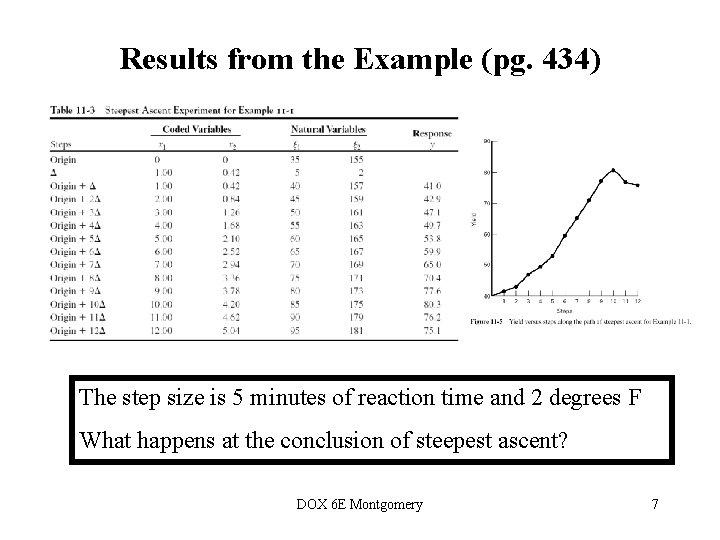
Results from the Example (pg. 434) The step size is 5 minutes of reaction time and 2 degrees F What happens at the conclusion of steepest ascent? DOX 6 E Montgomery 7

DOX 6 E Montgomery 8

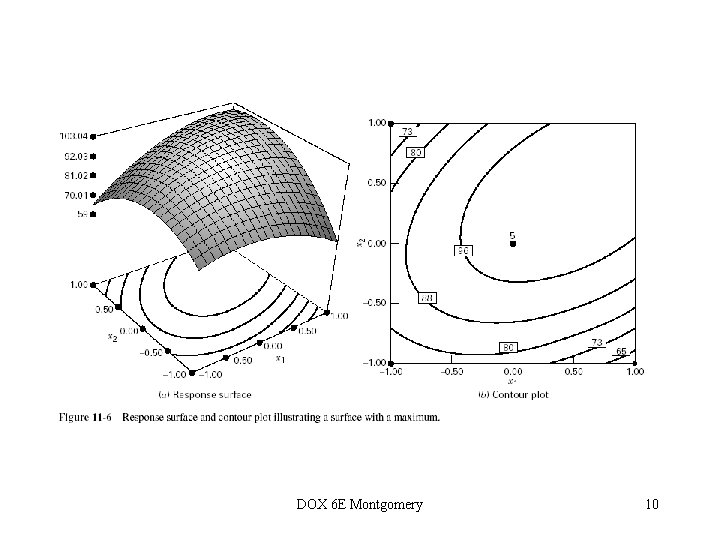
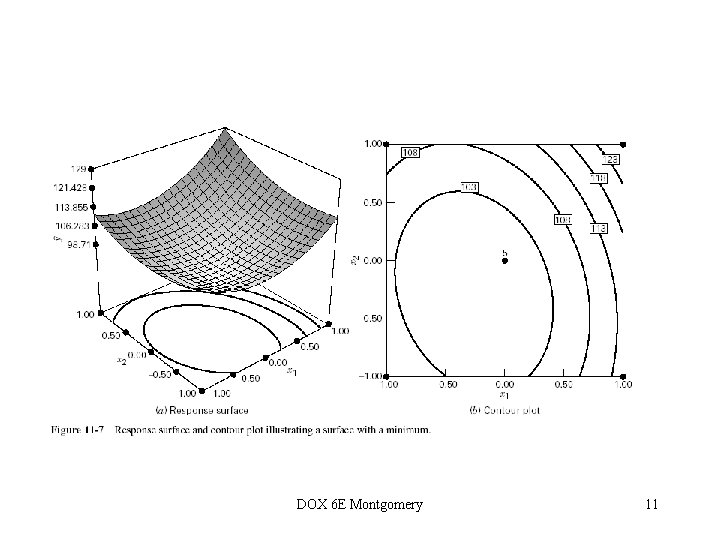
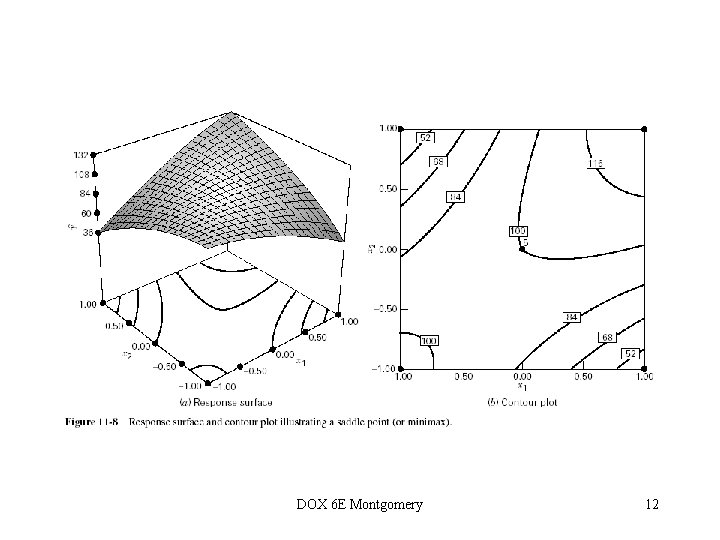
Second-Order Models in RSM • These models are used widely in practice • The Taylor series analogy • Fitting the model is easy, some nice designs are available • Optimization is easy • There is a lot of empirical evidence that they work very well DOX 6 E Montgomery 9

DOX 6 E Montgomery 10

DOX 6 E Montgomery 11

DOX 6 E Montgomery 12

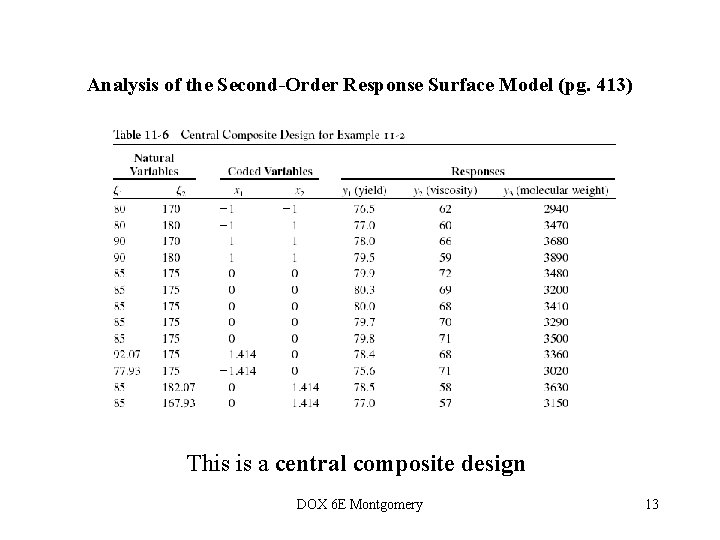
Analysis of the Second-Order Response Surface Model (pg. 413) This is a central composite design DOX 6 E Montgomery 13

DOX 6 E Montgomery 14

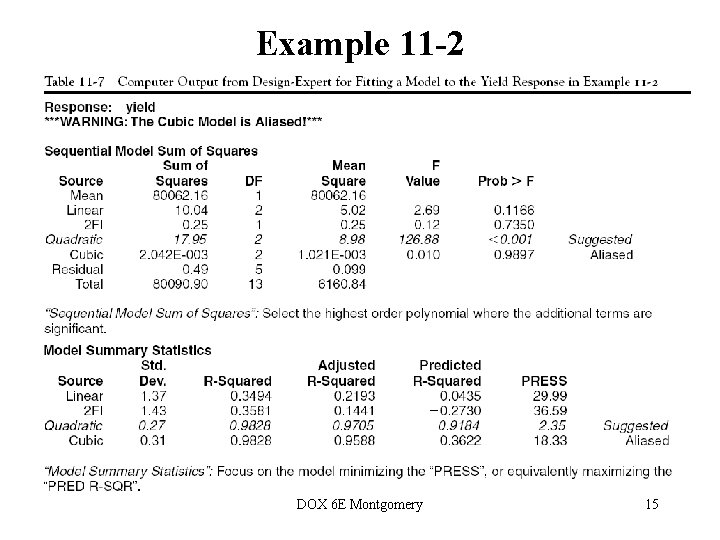
Example 11 -2 DOX 6 E Montgomery 15

Example 11 -2 DOX 6 E Montgomery 16

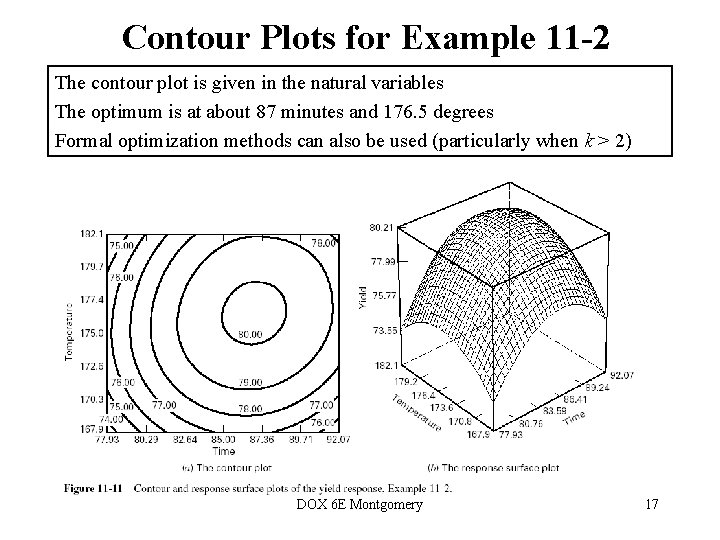
Contour Plots for Example 11 -2 The contour plot is given in the natural variables The optimum is at about 87 minutes and 176. 5 degrees Formal optimization methods can also be used (particularly when k > 2) DOX 6 E Montgomery 17

Multiple Responses • Example 11 -2 illustrated three response variables (yield, viscosity and molecular weight) • Multiple responses are common in practice • Typically, we want to simultaneously optimize all responses, or find a set of conditions where certain product properties are achieved • A simple approach is to model all responses and overlay the contour plots • See Section 11 -3. 4, pp. 423 -427. DOX 6 E Montgomery 18

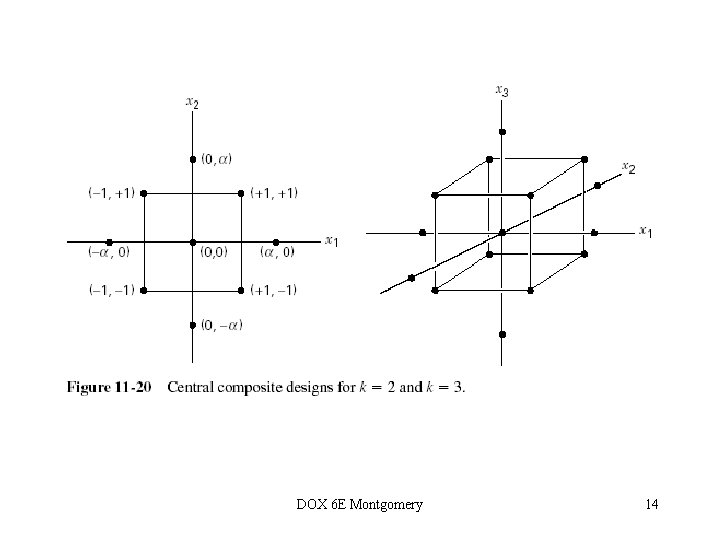
Designs for Fitting Response Surface Models • Section 11 -4, page 427 • For the first-order model, two-level factorials (and fractional factorials) augmented with center points are appropriate choices • The central composite design is the most widely used design for fitting the second-order model • Selection of a second-order design is an interesting problem • There are numerous excellent second-order designs available DOX 6 E Montgomery 19

Other Aspects of RSM • Robust parameter design and process robustness studies (Chapter 12) – Find levels of controllable variables that optimize mean response and minimize variability in the response transmitted from “noise” variables – Original approaches due to Taguchi (1980 s) – Modern approach based on RSM • Experiments with mixtures – – Special type of RSM problem Design factors are components (ingredients) of a mixture Response depends only on the proportions Many applications in product formulation DOX 6 E Montgomery 20