Design of Engineering Experiments Part 4 Introduction to

Design of Engineering Experiments Part 4 – Introduction to Factorials • • • Text reference, Chapter 5 General principles of factorial experiments The two-factorial with fixed effects The ANOVA for factorials Extensions to more than two factors Quantitative and qualitative factors – response curves and surfaces 1

Basic Principles and Advantages • A factorial design – all possible combinations of the levels of the factors are investigated in each complete trial or replication • Most efficient for two or more factor experiments • Both main effects and interaction effects can be dealt with • The effects of a factor can be estimated at several levels of the other factors – wider range of validity of conclusions 2

Some Basic Definitions Definition of a factor effect (main effect): The change in the mean response when the factor is changed from low to high 3

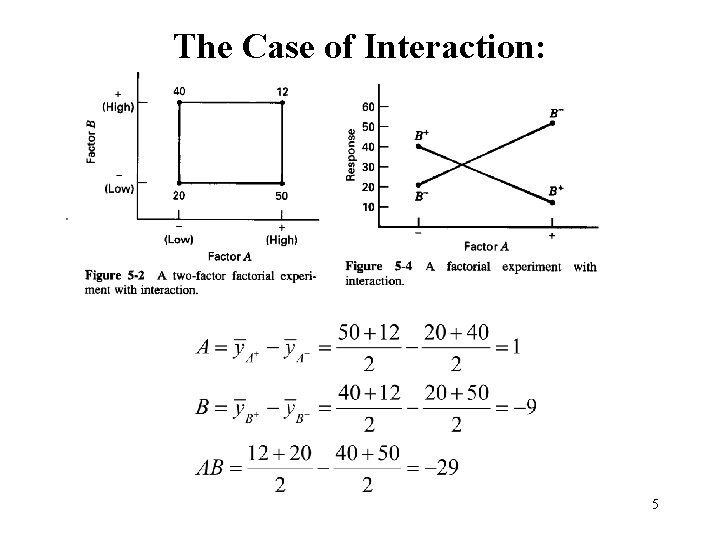
Some Basic Definitions Interaction occurs when differences in response between the levels of one factor is not the same at all levels of the other factors At the low level of B (B-): A = 40 – 20 = 20 At the high level of B (B+): A = 52 – 30 = 22 The magnitude of the interaction effect is the average difference in the two A effects: 4

The Case of Interaction: 5

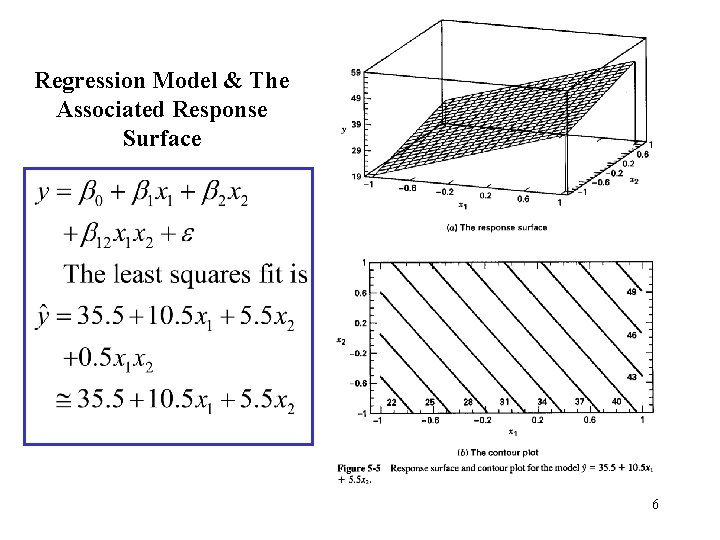
Regression Model & The Associated Response Surface 6

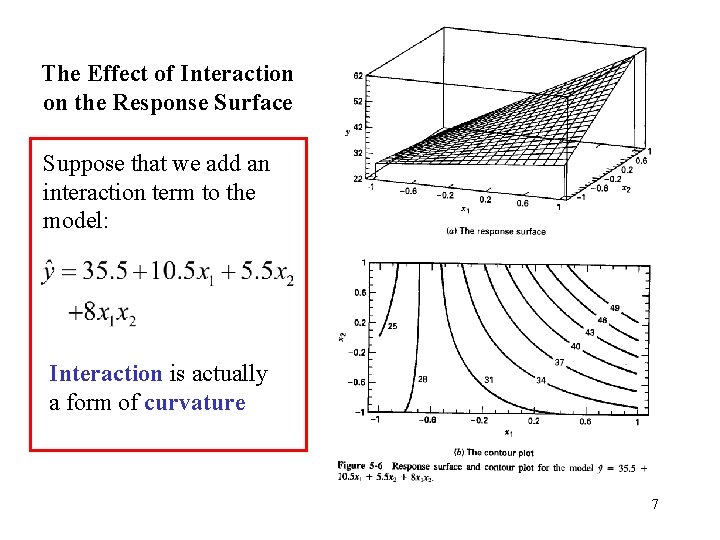
The Effect of Interaction on the Response Surface Suppose that we add an interaction term to the model: Interaction is actually a form of curvature 7

Some Basic Definitions • The knowledge of the interaction is more useful than knowledge of the main effect • A significant interaction will often mask the significance of main effects. • The main effect of one factor needs to be examined with the levels of other factors fixed when there is a significant interaction • The factorial design is more efficient than onefactor-at-a-time design, and the efficiency increases with the number of factors 8

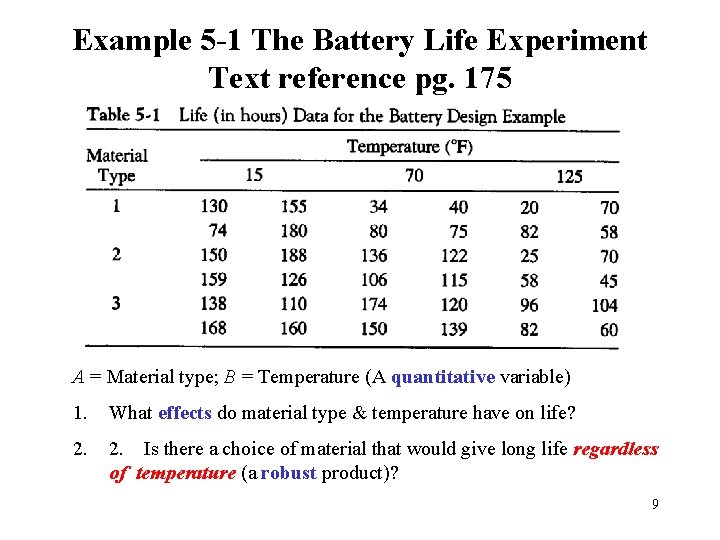
Example 5 -1 The Battery Life Experiment Text reference pg. 175 A = Material type; B = Temperature (A quantitative variable) 1. What effects do material type & temperature have on life? 2. Is there a choice of material that would give long life regardless of temperature (a robust product)? 9

The General Two-Factorial Experiment a levels of factor A; b levels of factor B; n replicates This is a completely randomized design 10

Statistical (effects) model: Other models (means model, regression models) can be useful 11

Hypotheses testing Equality of row treatment effects Ho: t 1 = t 2 = = ta = 0 H 1: at least one ti 0 Equality of column treatment effects Ho: b 1 = b 2 = = bb = 0 H 1: at least one bj 0 Equality of row and column treatment interactions Ho: (tb)ij = 0 for all i, j H 1: at least one (tb)ij 0 12

Extension of the ANOVA to Factorials (Fixed Effects Case) – pg. 167 13

ANOVA Table – Fixed Effects Case Design-Expert will perform the computations Text gives details of manual computing 14

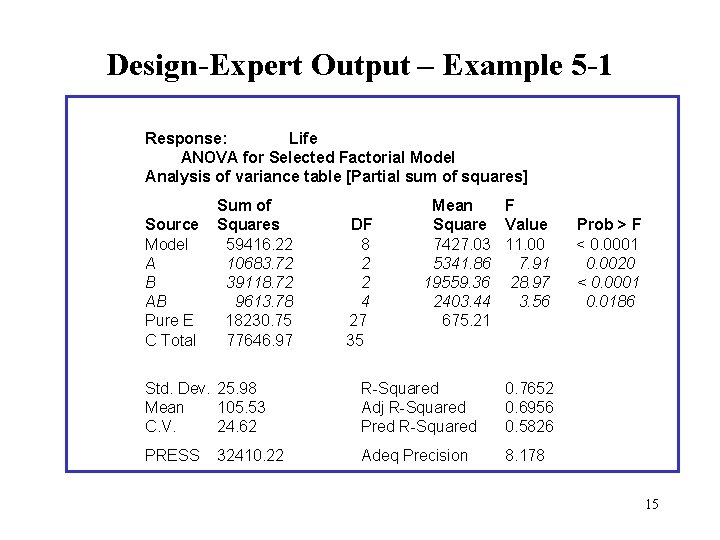
Design-Expert Output – Example 5 -1 Response: Life ANOVA for Selected Factorial Model Analysis of variance table [Partial sum of squares] Source Model A B AB Pure E C Total Sum of Squares 59416. 22 10683. 72 39118. 72 9613. 78 18230. 75 77646. 97 DF 8 2 2 4 27 35 Mean F Square Value 7427. 03 11. 00 5341. 86 7. 91 19559. 36 28. 97 2403. 44 3. 56 675. 21 Std. Dev. 25. 98 Mean 105. 53 C. V. 24. 62 R-Squared Adj R-Squared Pred R-Squared 0. 7652 0. 6956 0. 5826 PRESS Adeq Precision 8. 178 32410. 22 Prob > F < 0. 0001 0. 0020 < 0. 0001 0. 0186 15

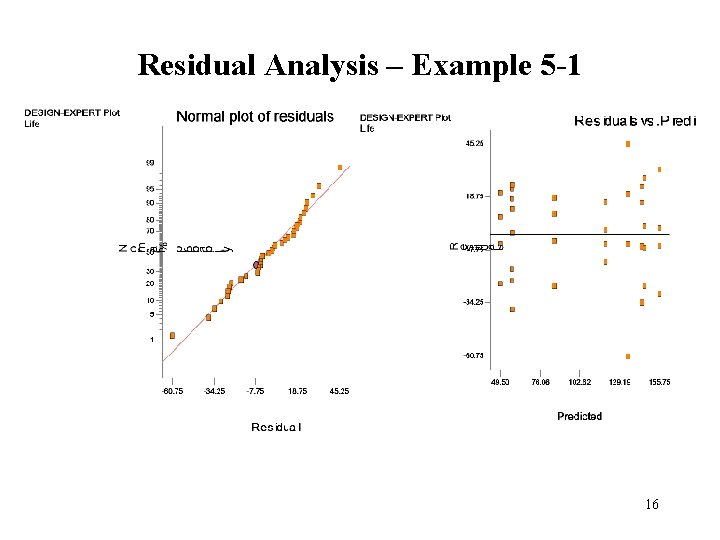
Residual Analysis – Example 5 -1 16

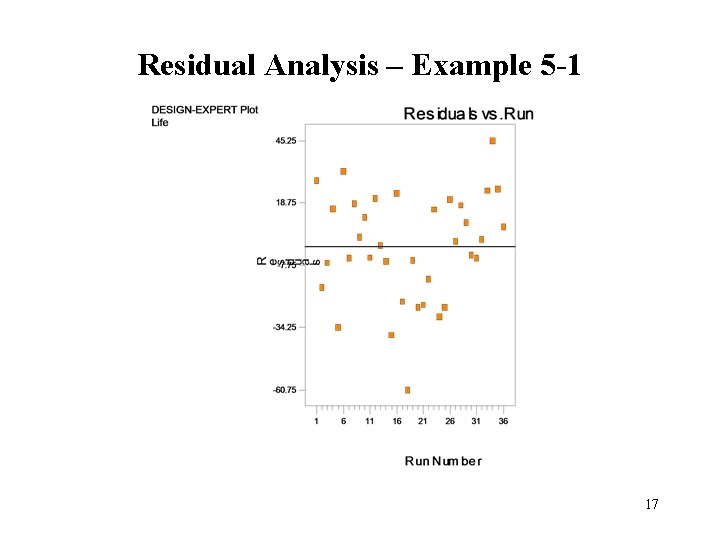
Residual Analysis – Example 5 -1 17

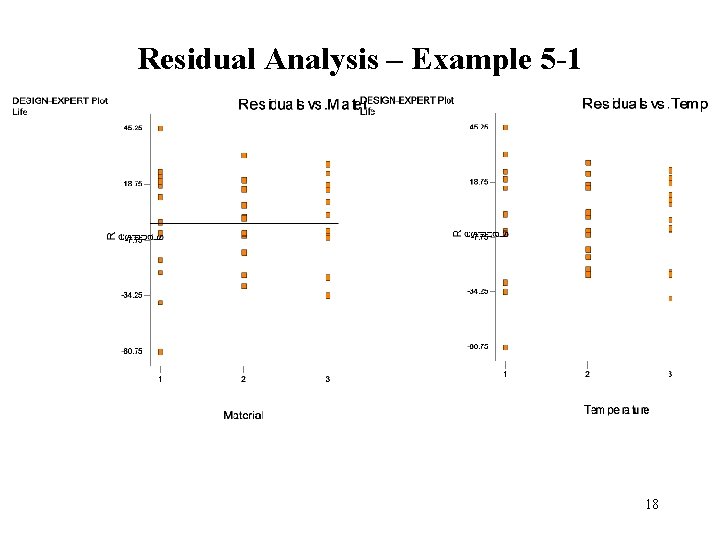
Residual Analysis – Example 5 -1 18

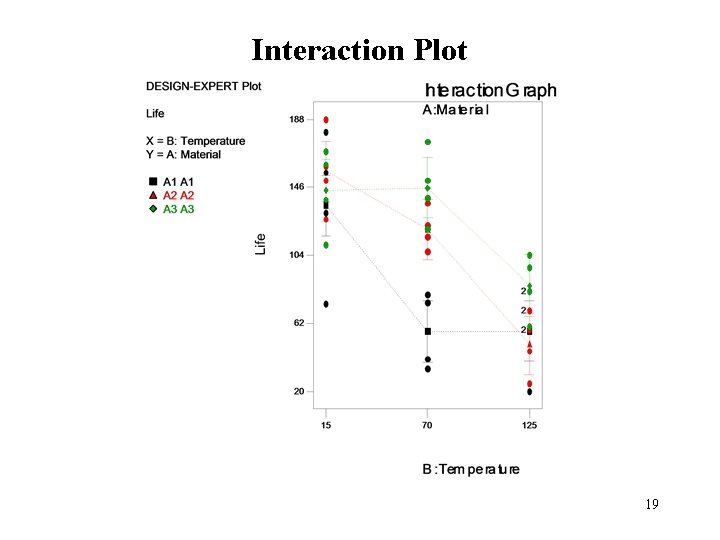
Interaction Plot 19

Choice of Sample Size • OC curves can be used to determine sample size (n) • An effective way is to specify a min. diff. between any two treatment means. E. g. if the difference in any two row means is D, the min. value of F 2 is • If the difference in any two columns is specified, • If the difference in any two interactions is specified, 20

One Observation per Cell • If there are two factors and only one observation per cell, the effect model is • Reminder: when n 2, • The two-factor interaction effect (tb)ij and the experimental error cannot be separated in obvious manner. Therefore, there are no tests on main effects unless the interaction effect is zero. And the model will be • The main effects may be tested by comparing MSA and MSB to MSResidual 21