Design of Elastomeric Bearing as per UIC 772

Design of Elastomeric Bearing as per UIC 772 2 -R

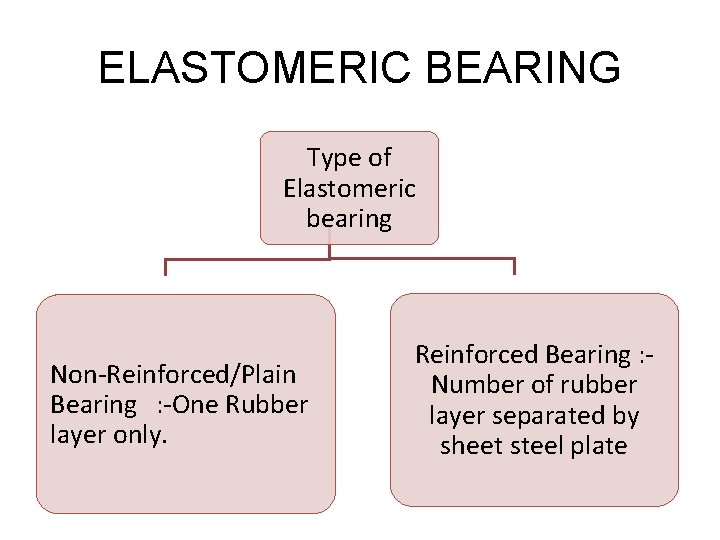
ELASTOMERIC BEARING Type of Elastomeric bearing Non-Reinforced/Plain Bearing : -One Rubber layer only. Reinforced Bearing : Number of rubber layer separated by sheet steel plate

Reinforced Elastomeric Bearing

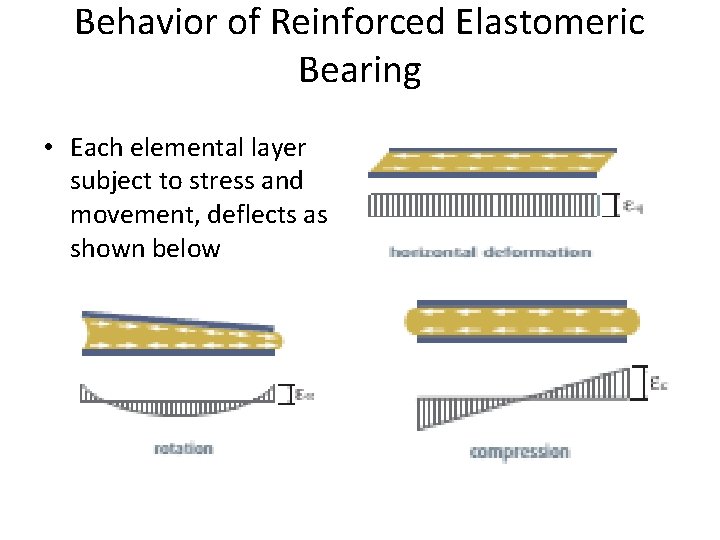
Behavior of Reinforced Elastomeric Bearing • Each elemental layer subject to stress and movement, deflects as shown below

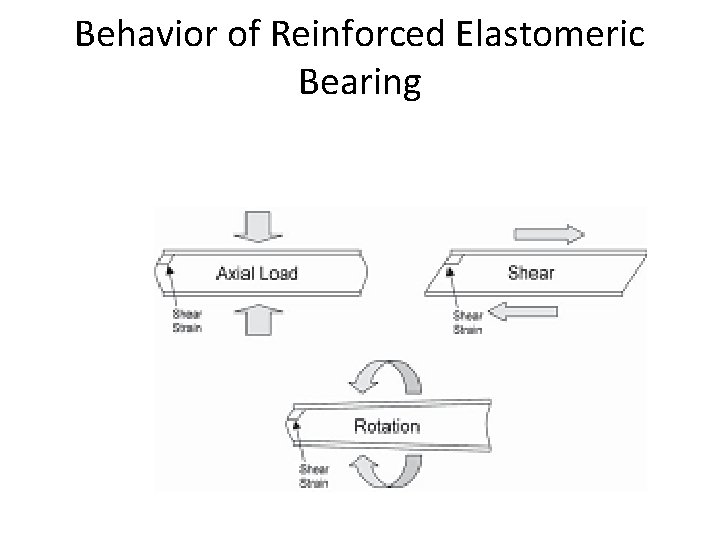
Behavior of Reinforced Elastomeric Bearing

Use of Reinforced Elastomeric Bearing Ø Long service life Ø Reliability, Ø Maintenance free, Ø Movement in all directions, Ø Lightness, Ø Small overall dimension, Ø Easy to install, Ø Used for filtering vibrations, Ø Earthquake proof insulation.

Limitations of Elastomeric Bearings Ø Ordinary elastomeric bearing can’t be used as a fixed bearing , Ø Translation allowed by elastomeric bearing is restricted by its thickness – 0. 7 of thickness, Ø Thick elastomeric pads are rather unstable , Ø Limit of vertical load which can be placed safely on elastomeric pads, – It causes excessive compression & bulging.

Maintenance Aspects • Bulging of neoprene

Maintenance Aspects • Tearing of neoprene

Maintenance Aspects • Tilting of bearing

Maintenance Aspects • Disintegration of bearing

Maintenance Aspects • Rupture of steel plate

Design philosophy • The design of steel reinforcement elastomeric bearing requires an appropriate balance of compressive, shear and rotational stiffness. • The shape factor, taken as the plan area divided by the area of the perimeter free to bulge, affects the compressive and rotational stiffness, but it has no impact on the translational stiffness or deformation capacity.

Design philosophy • The bearing must be designed to control the stress in the steel reinforcement and the strain in the elastomer. This is done by controlling the elastomer layer thickness and the shape factor of the bearing. Fatigue, stability, yield and rupture of the steel reinforcement, stiffness of the elastomer, and geometric constraints must all be satisfied.

UIC 772 2 -R

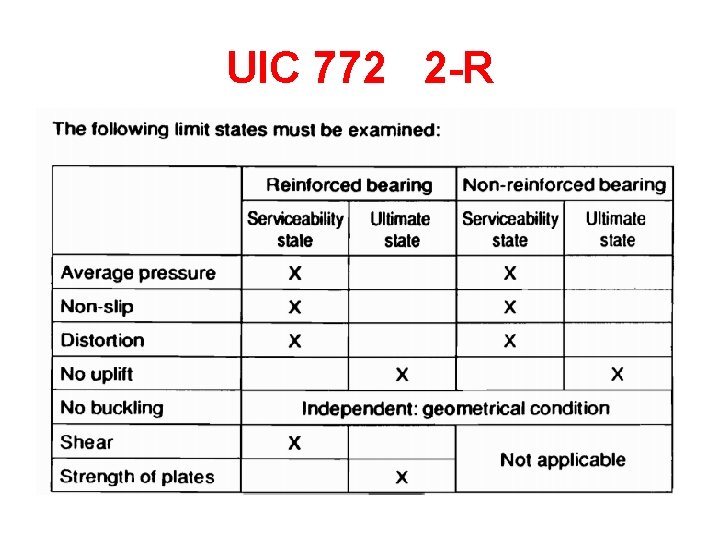
UIC 772 2 -R

A. Mean pressure (SLS) (Cl. 4. 3. 3. 1 of UIC 772 2 -R) 2 Ø σm = P/{b x (a-u)}< 11 Mpa(N/mm ) Where, P= Total load (Pc + Ps), b= Dimension of bearing across traffic direction, a= Dimension of bearing along traffic direction, u= Total shear strain= (uc+us), uc = Shear strain due to slow tangential load us = Shear strain due to rapid tangential load Note: - Lowest possible effective area will be obtained after deduction of ‘u’.

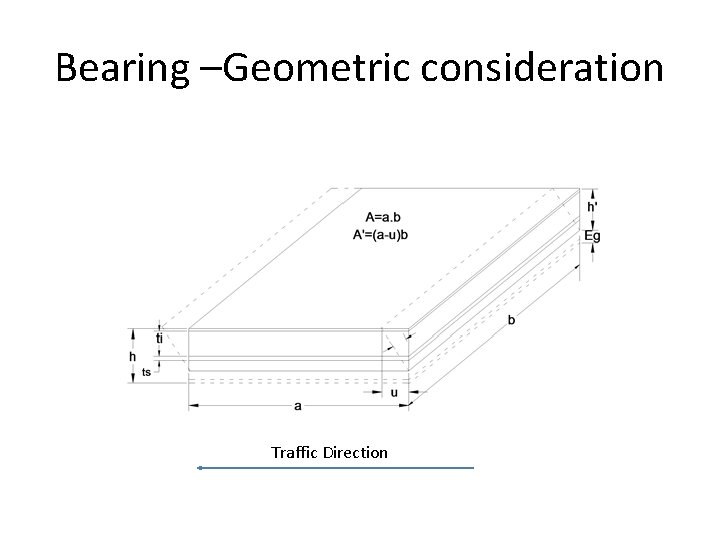
Bearing –Geometric consideration Traffic Direction

B. i No-Slip (SLS) (Cl. 4. 3. 3. 2 of UIC 772 2 -R) Ø σ'm= Pmin/A ≥ 2 N/mm 2 Where, • Pmin= Pc=Normal slow load i. e. due to DL& SIDL, • Pmin ≥ 2 x. A , Otherwise the girder will slide over the elastomer. The bearing will be ineffective. • Here ‘A’(contact area) is considered without deduction of ‘u’.

B. ii. a No-Slip (SLS) (Cl. 4. 3. 3. 2 of UIC 772 2 -R) Ø In case of slow load Ø Horizontal force< f x (Normal Slow load) Ø H< f *Pc Where, f= 0. 12+0. 2 /σm’ & σm’ = Pc/A H< {0. 12+0. 2*A /Pc) x. Pc i. e. H< (0. 12*Pc+0. 2*A )& (G *a* uc)/T=H i. e. (G *a* uc)/T < (0. 12*Pc +0. 2*A ) Hence, T>(GA uc)/(0. 12 P+0. 2 A) Where, T=Total thickness of elastomer, G=Modulus of rigidity of elastomer.

B. ii. b No-Slip (SLS) (Cl. 4. 3. 3. 2 of UIC 772 2 -R) Ø In case of Rapid load Ø Horizontal force< fx(Total Normal load) Ø H< f *(Pc + Ps) Where, f= 0. 12+0. 2 /σm & σm = P/A H< {0. 12+0. 2*A /P) x. P i. e. H< (0. 12*P+0. 2*A )& (GA uc +2 GA us)/T=H i. e. (GA uc +2 GA us)/T < (0. 12*P+0. 2*A ) Hence, T>(GA uc +2 GA us)/(0. 12 P+0. 2 A)

C. Limitation of Distortion (SLS) (Cl. 4. 3. 3. 3 of UIC 772 2 -R) Ø τH /G≤ 0. 7 Where, τH= τH c+ τH s = Guc /T + Gus /T={G(uc + us)} /T i. e. τH /G= (uc + us) /T ≤ 0. 7 Hence, T≥ (uc+us)/0. 7 → (uc+us) ≤ 0. 7 *T Maximum permissible tangential shear strain should be 70% of the total thickness of elastomer excluding cover.

D. a. i-No uplift at the edge (ULS) (Cl. 4. 3. 3. 4 of UIC 772 2 -R) Ø Calculation of Shape factor • Si = a*b/(2*ti*(a+b)) Where, Si =Shape factor of an elementary layer of elastomer. In case of a reinforced bearing the casing / cover is not taken into account. ti = Thickness of elementary layer of elastomer.

D. a. ii-No uplift at the edge (ULS) (Cl. 4. 3. 3. 4 of UIC 772 2 -R) Ø Calculation tangent of rotation (considered as positive): |tg αc| < 6 ∑eic / a Ø ∑eic = n*eic Ø eic = ti*σmc/(4*G*(Si)^2+(3*σmc)) Where, eic = Total deformation in compression under the action of a slow load for reinforced bearing. Ø Mean comp. stress due to slow load (ULS): σmc = Pcf/(a*b)

D. b. i-No uplift at the edge (ULS) (Cl. 4. 3. 3. 4 of UIC 772 2 -R) Ø Calculation tangent of rotation (considered as positive): |tg αc +1. 5 tg αs| < 6 ∑ei / a Ø tg αc = (tan αo+tan αc) Ø tg αs = tan αs Ø ei = ti*σm 2/(4*G*(Si)^2+(3*σm 2)) Where, ei=Total deformation in compression under the simultaneous action of a slow and rapid load for reinforced bearing. Ø Mean comp. stress due to slow & rapid load (ULS): σm 2 = (Pcf+Psf)/A

E. No Buckling(Independent check) (Cl. 4. 3. 3. 5 of UIC 772 2 -R) Ø a/10 ≤ T ≤ a/5 Ø i. e. 0. 1*a ≤ T ≤ 0. 2*a If ‘b’ is less than ‘a’. Then 0. 1*b ≤ T ≤ 0. 2*b Generally , ‘a’ shall be less than ‘b’.

F. Shear(SLS) (Cl. 4. 3. 3. 6 of UIC 772 2 -R) Ø ζp+ζh+ζα <5 G Where, Ø Shear stress due to normal force, ζp = 1. 5*( Pc+1. 5 Ps)/Si* a*b Ø Mean shear stress due to a tangential force ’H’ ζh = G(uc+us)/T Ø Shear stress due to rotation, ζα = G*a^2*(tgαo+tgαc+1. 5 tgαs)/(2*T*ti)

G. Strength of plates-Fracture state (ULS) (Cl. 4. 3. 3. 7 of UIC 772 2 -R) Ø ts>a*σm 2*γs/(Si*σa) Where, ts= Thickness of steel plate (shall not be less than 1 mm). The minimum thickness of steel plate so as to able to withstand the tensile force to which they are subject under normal loading calculated for ultimate load. σa= Yield strength of steel plate (Max. 420 N/mm 2 & Min. 240 N/mm 2), γ s= Partial safety factor of steel at limit state,

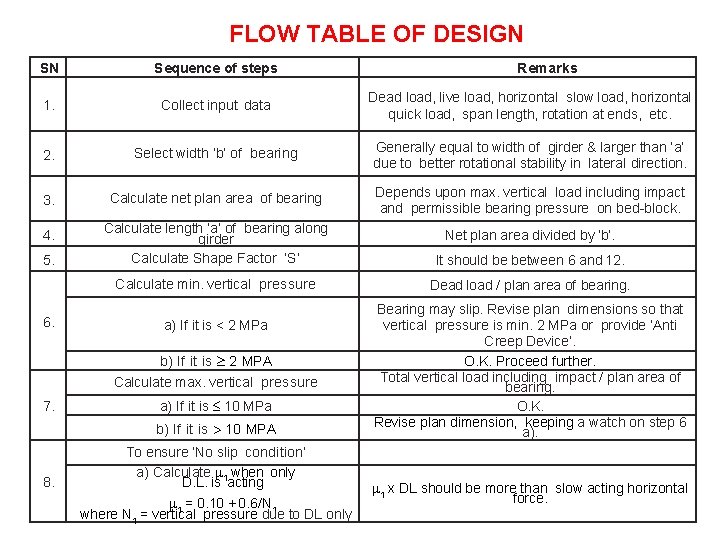
FLOW TABLE OF DESIGN SN Sequence of steps 1. Collect input data Dead load, live load, horizontal slow load, horizontal quick load, span length, rotation at ends, etc. 2. Select width ‘b’ of bearing Generally equal to width of girder & larger than ‘a’ due to better rotational stability in lateral direction. 3. Calculate net plan area of bearing Depends upon max. vertical load including impact and permissible bearing pressure on bed-block. 4. Calculate length ‘a’ of bearing along girder Calculate Shape Factor ‘S’ Net plan area divided by ‘b’. It should be between 6 and 12. Calculate min. vertical pressure Dead load / plan area of bearing. 5. 6. a) If it is < 2 MPa b) If it is 2 MPA Calculate max. vertical pressure 7. a) If it is 10 MPa b) If it is 10 MPA 8. To ensure ‘No slip condition’ a) Calculate 1 when only D. L. is acting 1 = 0. 10 + 0. 6/N 1 where N 1 = vertical pressure due to DL only Remarks Bearing may slip. Revise plan dimensions so that vertical pressure is min. 2 MPa or provide ‘Anti Creep Device’. O. K. Proceed further. Total vertical load including impact / plan area of bearing. O. K. Revise plan dimension, keeping a watch on step 6 a). 1 x DL should be more than slow acting horizontal force.

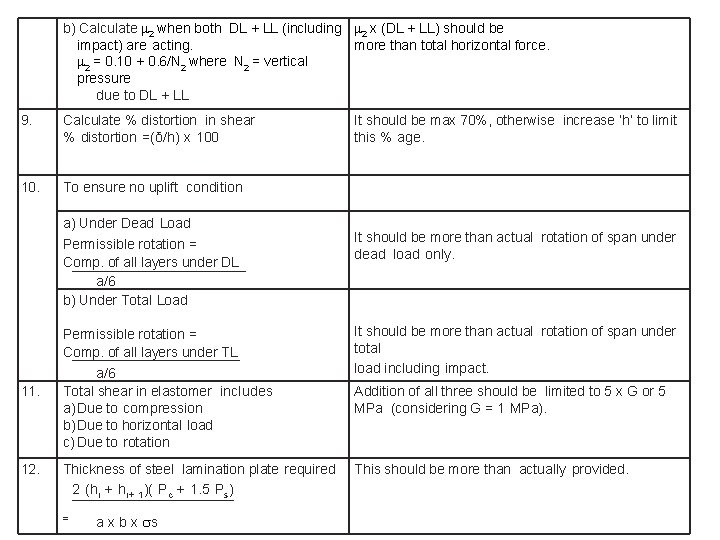
b) Calculate 2 when both DL + LL (including 2 x (DL + LL) should be impact) are acting. more than total horizontal force. 2 = 0. 10 + 0. 6/N 2 where N 2 = vertical pressure due to DL + LL 9. Calculate % distortion in shear % distortion =(δ/h) x 100 10. To ensure no uplift condition a) Under Dead Load Permissible rotation = Comp. of all layers under DL a/6 b) Under Total Load 11. 12. Permissible rotation = Comp. of all layers under TL a/6 Total shear in elastomer includes a) Due to compression b) Due to horizontal load c) Due to rotation Thickness of steel lamination plate required 2 (hi + h i+ 1)( Pc + 1. 5 Ps) = a x b x s It should be max 70%, otherwise increase ‘h’ to limit this % age. It should be more than actual rotation of span under dead load only. It should be more than actual rotation of span under total load including impact. Addition of all three should be limited to 5 x G or 5 MPa (considering G = 1 MPa). This should be more than actually provided.

THANK YOU