DESIGN OF DISTRIBUTION SYSTEM Design of distribution system

DESIGN OF DISTRIBUTION SYSTEM

Design of distribution system - steps Step 1: Location of the warehouse in the customer network. Step 2: Supply of warehouses from production plants. Step 3: Delivery of goods from warehouses to customers.

Warehouse location Find a location that ensures minimum shipping costs from the warehouse to i, j = 1, 2, …. . N customers distance, transported quantity of goods, type of transport, freight rates/tariffs Input data requirements Shipping costs are influenced by: • Distance • Cartesian • Transported quantity of goods • transported • Type of transport • freight coordinates of the customer location ( xj , yj ) or real distance dij quantity of goods qij in appropriate units rates, tariffs cij

Warehouse location – distances determination coordinates of the customer location and calculation: Euclidean: di, j = ((xi-xj)2+(yi-yj)2)0. 5 Euclidean with correction: di, j = k *((xi-xj)2+(yi-yj)2)0. 5 for k>1 „on axis“: di, j = ( xi-xj + yi-yj ) quadratic: di, j = ((xi-xj)2+(yi-yj)2) real distance: generating a matrix of distances from GIS reading from the map

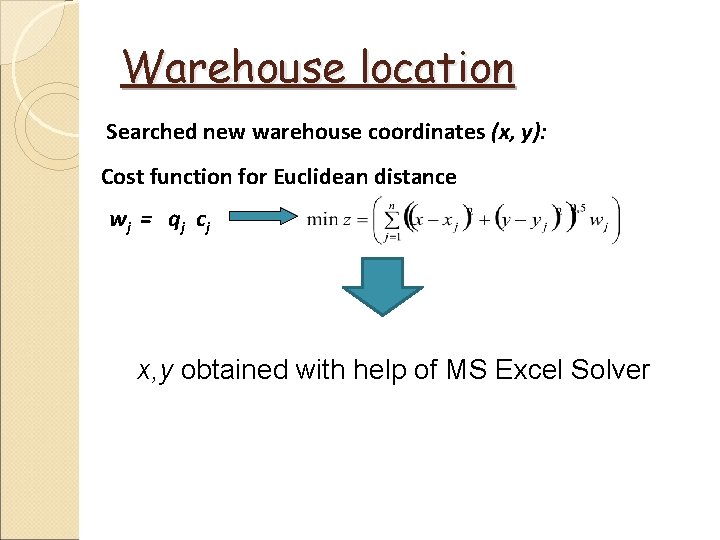
Warehouse location Searched new warehouse coordinates (x, y): Cost function for Euclidean distance wj = q j c j x, y obtained with help of MS Excel Solver

Transportation problem- introduction How to supply warehouses from production plants to minimize shipping costs? i = 1, 2, … m number of production plants ai … capacity of i-th production plant j = 1, 2, … n number of warehouses bj … requirements of j-th warehouse

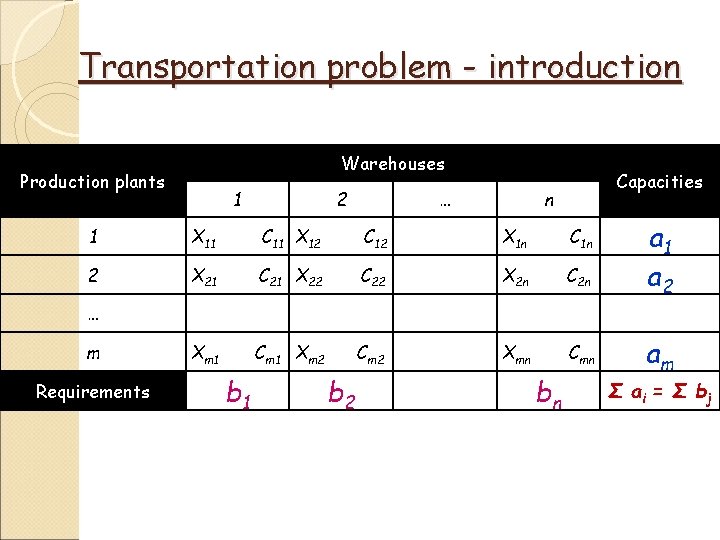
Transportation problem - introduction Warehouses Production plants 1 2 … Capacities n 1 X 11 C 11 X 12 C 12 X 1 n C 1 n 2 X 21 C 21 X 22 C 22 X 2 n C 2 n a 1 a 2 Xm 1 Cm 1 Xm 2 Cm 2 Xmn Cmn am … m Requirements b 1 b 2 bn Σ ai = Σ b j

Transportation problem – variables, parameters xij transported quantity from i-th plant to j-th warehouse (kg, t, pcs, boxes, palettes etc. ) dij distance between i-th plant and j-th warehouse (km) cij shipping costs between i-th plant and j-th warehouse (CZK/t, km; CZK/pc, km etc. ) cij = f(xij, dij)

Transportation problem – (un)balanced 1. Balanced: 2. Unbalanced: Producers do not have sufficient capacity to satisfy warehouses. Manufacturers' capacities exceed warehouse requirements.

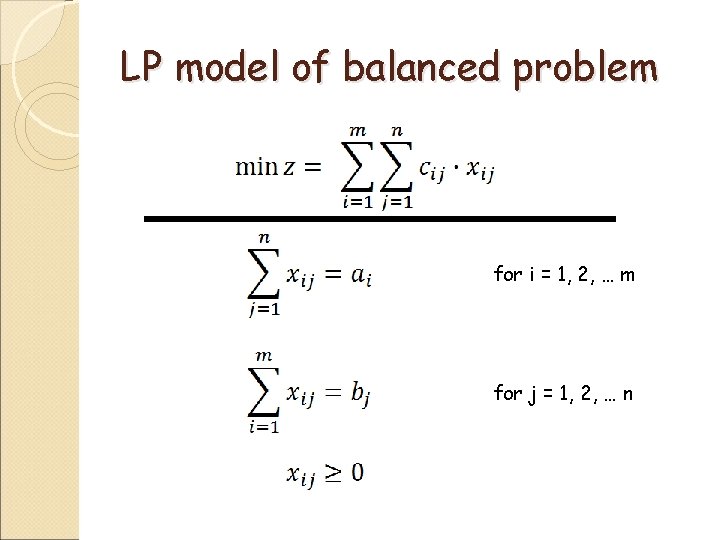
LP model of balanced problem for i = 1, 2, … m for j = 1, 2, … n

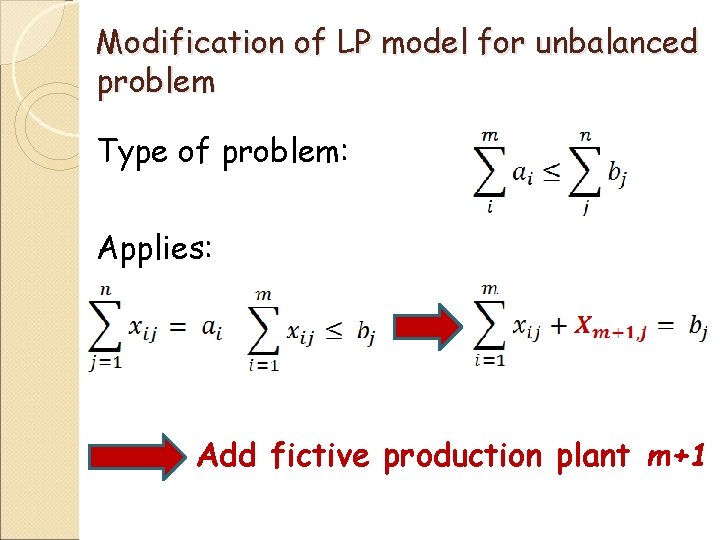
Modification of LP model for unbalanced problem Type of problem: Applies: Add fictive production plant m+1

Fictive production plant Capacity: Shipping costs: Cm+1, j = 0 Xm+1, j = 0 represent undelivered quantities to j- th warehouse

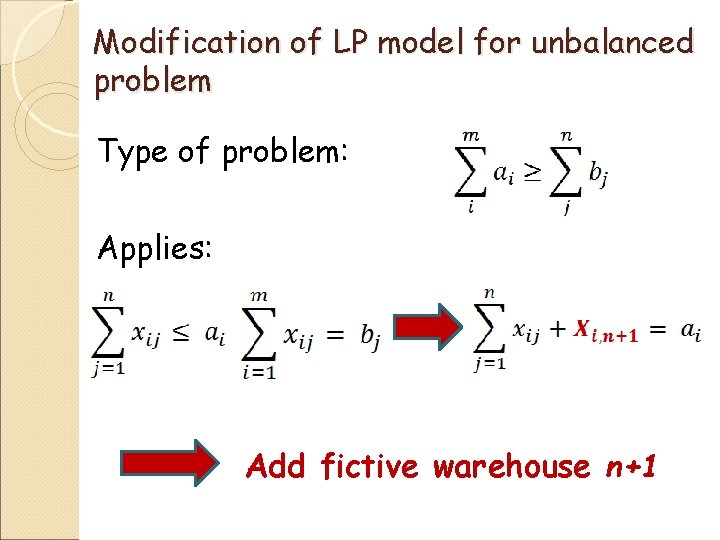
Modification of LP model for unbalanced problem Type of problem: Applies: Add fictive warehouse n+1

Fictive warehouse Requirements: Shipping costs: Ci, n+1 = 0 Xi, n+1 = 0 represents unused capacity of i-th production plant

Transportation problem - solution Linear programming: 1. ◦ ◦ 2. ◦ ◦ Simplex method. Solver MS Excel. Approximation methods: Least cost method. Vogel’s approximation method(VAM).

Vehicle routing problem Based on the warehouse location: How to deliver goods from warehouses to customers efficiently? Clarke&Wright „savings“ algorithm

Clarke &Wright „savings“ algorithm Let i-th warehouse represents depot Di Let customers represent j = 1, 2, . . . , n starting demand points and j' = 1, 2, . . . , n ending demand points Let d(Di, j) represents the distance between a demand point and the depot Let d(j, j') represents the distance between two different demand points (j ≠ j')

Clarke &Wright „savings“ algorithm If n carriers satisfy the demand of customers individually so that one carrier serves one customer total traveled distance TL is: If one carrier visits two customers [i. e. two different demand points (j, j')] during one travel total traveled distance is shorter of a saving s(j, j‘):

Clarke &Wright „savings“ algorithm Step 1: Calculate savings s(j, j') for each pair of demand points (j, j'). Step 2: Sort savings s(j, j') in descendind order. Step 3: For the maximal available saving s(j, j'), add (j, j') to a route, if the capacity of carrier is sufficient, if the lenght of a route is acceptable and if: a: Either, neither j nor j‘ is the part of a route, in this case new route is established with both j and j‘ demand points. b: Or, one of the demand points (j or j') is already the part of a route. In case that this demand point is not placed within the route (j, j') is added to the same route. c: Or, both demand points j and j' are the part of a route and none of these demand points are placed within these routes, in that case these routes are merged. Step 4: If a saving s(j, j') > 0 is still available go back to Step 3.

DESIGN OF DISTRIBUTION SYSTEM Jakub Dyntar jakub. dyntar@tul. cz