DESIGN OF CYCLOIDS HYPOCYCLOIDS AND EPICYCLOIDS CURVES WITH











- Slides: 17

DESIGN OF CYCLOIDS, HYPOCYCLOIDS AND EPICYCLOIDS CURVES WITH DYNAMIC GEOMETRY SOFTWARE. ENGINEERING APPLICATIONS M. Flórez, M. V. Carbonell, E. Martínez Dpto. Física y Mecánica. Escuela Técnica Superior de Ingenieros Agrónomos. Universidad Politécnica de Madrid (España)

Objetives To draw the mechanical curves most used in engineering (cycloid, hypocycloid, epicycloids) by using the Geogebra software. Study some engineering applications of these mechanical curves, the planetary gear trains, and the kinematic requirements.

The Geogebra Software

Cycloid curves The cycloids curves, are planar curves obtained by the motion of a point of a circle or a line that rolls without slipping on another circle or a line. The line or moving circle is called wheel of rolling circle (it is also called roulette), and the line or circle on moving the wheel is the base of fixed circle. When the rolling circle is rotating on another circumference, the path described is an epicycle; . If the rolling circle is outside the circumference, the path obtained is an epicycloid and if the rolling circle is inside the circumference the path obtained is a hypocycloid (the Greek epi and hypo mean exterior and interior respectively).

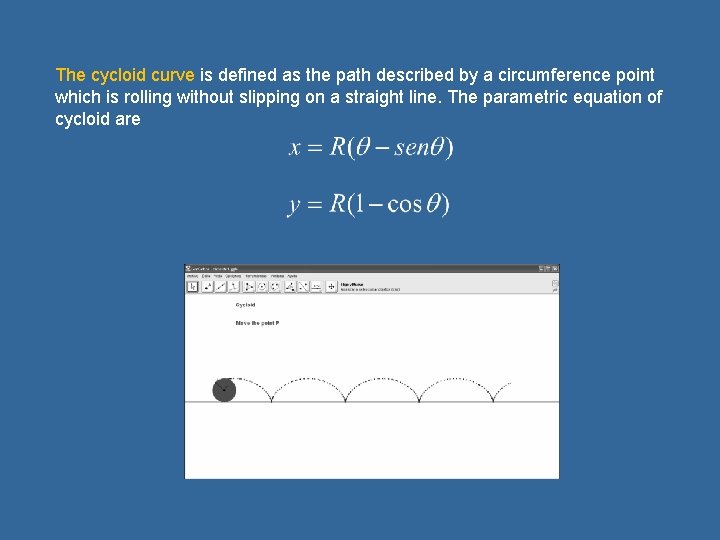
The cycloid curve is defined as the path described by a circumference point which is rolling without slipping on a straight line. The parametric equation of cycloid are

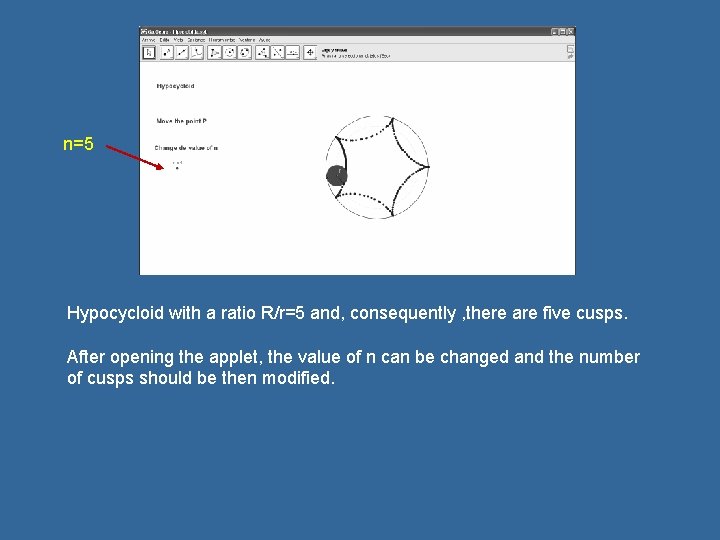
Hypocycloids are particular cases of cycloid is the hypocycloid ("hypo"beneath); in this case the rolling circle rotates on the inside of another circle. When a circle of radius r rolls along the inside of a circle of radius R, the form of the trajectories of the boundary points of the rolling circle (the “wheel”) depends on n = R/r and they have n cusps and n arches. The parametric equation of hypocycloid is

n=5 Hypocycloid with a ratio R/r=5 and, consequently , there are five cusps. After opening the applet, the value of n can be changed and the number of cusps should be then modified.

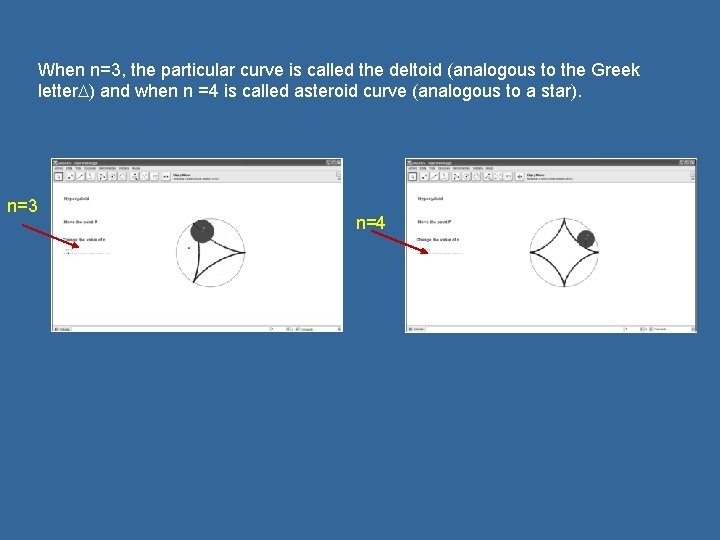
When n=3, the particular curve is called the deltoid (analogous to the Greek letter ) and when n =4 is called asteroid curve (analogous to a star). n=3 n=4

Epicycloids are curves traced when the rolling circle rotates outside the circumference of another circle without slipping ("epi"- upon). A circle of radius r rolling along the outside of a circle of radius R and the form depends on the ratio n=R/r.

Epicycloid with a ratio R/r=5 and, consequently , there are five cusps After opening the applet, the P point should be moved and the path described by the point A belonging to the periphery of the rotating circle will be drawn.

Engineering applications: Planetary gear train A planetary gear train is formed by a fixed ring gear, a planetary gear, b , and a planetary carrier, c. When the carrier acts as the input link and rotates one revolution, a point on the pitch circle of the planetary gear will describe a hypocycloid/epicycloid path.

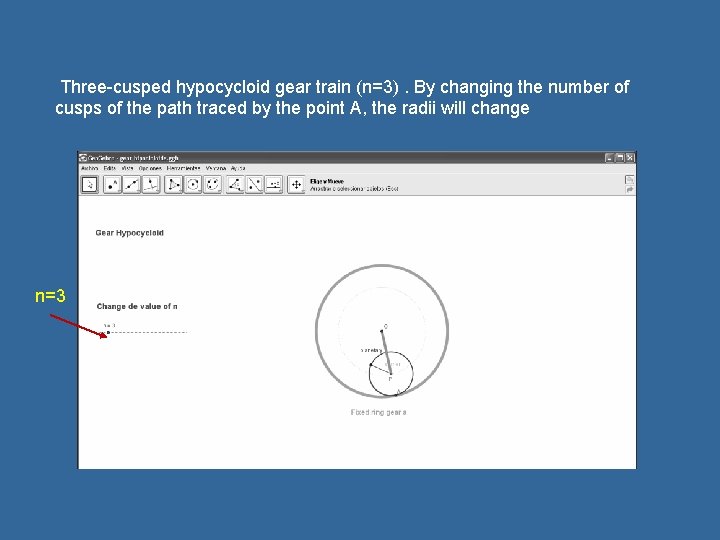
Hypocycloid planetary gear train is formed by a fixed ring gear, a, a planetary gear, b, and a planetary carrier, c. When the carrier acts as the input link and rotates one revolution, a point on the pitch circle of the planetary gear will describe a hypocycloid path. The relationship between the angular velocities of the ring gear (in this case the ring gear is fixed and the a=0), the planetary gear ( b) and the planetary carrier c in an n-cusped hypocycloid planet gear train is In a planetary hypocycloid system, the singular link has the n′ = (n − 1) multiples angular velocity as the binary link but rotates at an opposite direction. The main feature of a hypocycloid mechanism is that a fixed point A on the singular link may describe a hypocycloid when the binary link is rotated.

Three-cusped hypocycloid gear train (n=3). By changing the number of cusps of the path traced by the point A, the radii will change n=3

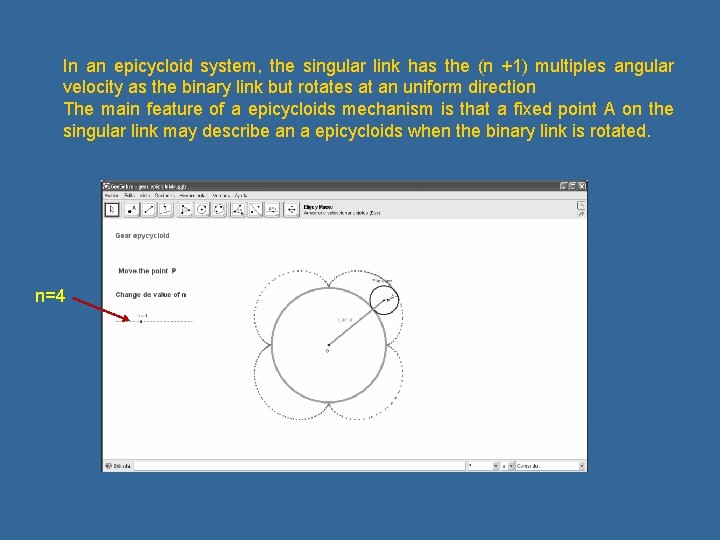
An epicycloid planetary gear train is formed by a fixed ring gear, a planetary gear, b , and a planetary carrier, c. In this case the length of the carrier will be greater than the radius of the fixed ring gear. The relationship between the angular velocities of the ring gear (in this case the ring gear is fixed and the a=0), the planetary gear ( b) and the planetary carrier c in an n-cusped hypocycloid planet gear train is

In an epicycloid system, the singular link has the (n +1) multiples angular velocity as the binary link but rotates at an uniform direction The main feature of a epicycloids mechanism is that a fixed point A on the singular link may describe an a epicycloids when the binary link is rotated. n=4

All the simulations have been generated with the Geogebra software. Authors are members of the Educational Innovation Group of the Technical University of Madrid “New Trends in Physics Teaching”. The authors are grateful to the Universidad Politécnica de Madrid for the financial support of projects about Innovation and Teaching

Thanks for your attention
 Applications of hypocycloid
Applications of hypocycloid Space curves
Space curves Creating production possibilities schedules and curves
Creating production possibilities schedules and curves Carrying capacity population
Carrying capacity population Heat curve
Heat curve Highway curves banked and unbanked
Highway curves banked and unbanked S and j curves
S and j curves Physical behavior of matter
Physical behavior of matter Mirror that curves outward and used in convenience store
Mirror that curves outward and used in convenience store Mirror curved outward
Mirror curved outward What is engineering curves
What is engineering curves Elliptic curves number theory and cryptography
Elliptic curves number theory and cryptography Physical behavior of matter heating and cooling curves
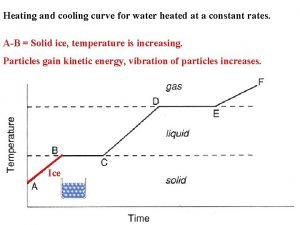
Physical behavior of matter heating and cooling curves Heating and cooling curves
Heating and cooling curves Fills in gaps in data and fit data into curves
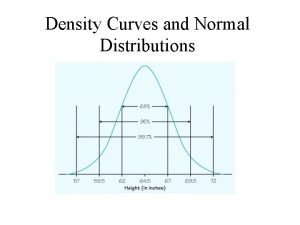
Fills in gaps in data and fit data into curves Normal curves and sampling distributions
Normal curves and sampling distributions The sine and cosine curves intersect infinitely
The sine and cosine curves intersect infinitely Interpolation and approximation of curves in cad
Interpolation and approximation of curves in cad