Design of Compression Members Chapter 03 B 1

Design of Compression Members Chapter 03 B 1 Wednesday, October 20, 2021

TYPES OF COLUMNS DEPENDING ON BUCKLING BEHAVIOR Elastic Critical Buckling Stress The elastic critical buckling stress is defined as under: Fe = Elastic critical buckling (Euler) stress = The critical slenderness ratio dividing the expected elastic and inelastic buckling is denoted by Rc and is given below: 2 Wednesday, October 20, 2021

Long Columns In long columns, elastic buckling is produced and the deformations due to this type of buckling are recovered upon removal of load. Further, the stresses produced due to elastic buckling remains below the proportional limits. The Euler formula is used to find strength of long columns where elastic buckling is the controlling failure mechanism. 3 Wednesday, October 20, 2021

Long columns are defined as those columns for which the slenderness ratio is greater than the critical slenderness ratio Rc. The design column strength curve with the inclusion of φ factor, is shown in Figure 3. 17. Short Columns For very short columns, when the slenderness ratio is less than 20 to 30, the failure stress will equal the yield stress and no buckling occurs. In practice, very few columns meet. Wednesday, this October 20, 4 2021 condition.

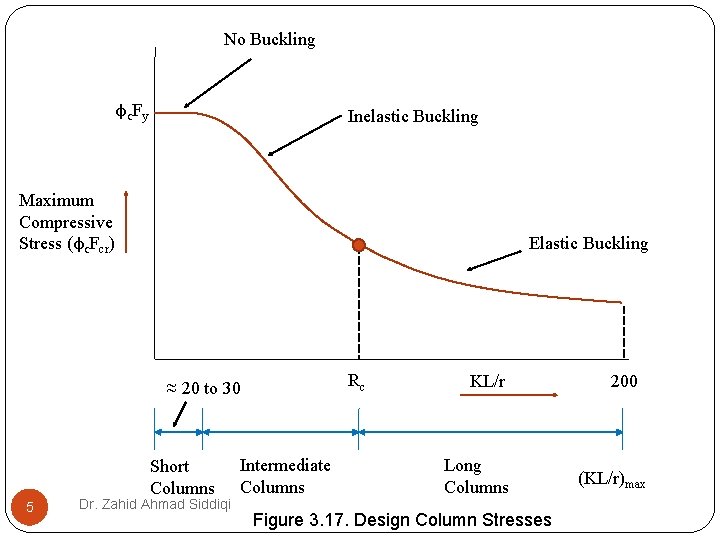
No Buckling φc. Fy Inelastic Buckling Maximum Compressive Stress (φc. Fcr) Elastic Buckling Rc ≈ 20 to 30 Short Columns 5 Dr. Zahid Ahmad Siddiqi Intermediate Columns KL/r Long Columns Figure 3. 17. Design Column Stresses 200 (KL/r)max

For design, these are considered with the intermediate columns subjected to the condition that failure stress should not exceed the yield stress. Intermediate Columns Intermediate columns buckle at a relatively higher load (more strength) as compared with long columns. The buckling is inelastic meaning that part of the section becomes inelastic after bending Wednesday, October 20, 6 2021 due to buckling.

The columns having slenderness ratio lesser than the critical slenderness ratio (Rc) are considered as intermediate columns, as shown in Figure 3. 17. COLUMN STRENGTH FORMULAS The design compressive strength (Øc. Pn) and the allowable compressive strength (Pn/Ωc) of compression members, whose elements do not exhibit elastic local instability (only compact and non compact sections) are given Wednesday, October 20, 7 below: 2021

Ωc = 1. 67 (ASD) : Pn = Fcr Ag Fcr= critical or ultimate compressive strength based on the limit state of flexural buckling determined as under: Elastic Buckling when KL/r > Rc or Fe < 0. 44 Fy Fcr = 0. 877 Fe Formula E 3 2) (AISC where ‘Fe’ is the Euler’s buckling stress and Wednesday, October 20, 8 0. 877 is a factor to estimate the effect of out of 2021

Inelastic Buckling and No Buckling when KL/r ≤ Rc or Fe ≥ 0. 44 Fy (AISC Formula E 3 3) 9 Wednesday, October 20, 2021

TYPES OF COLUMN SECTIONS FOR LOCAL STABILITY 1. Compact Sections A compact section is one that has sufficiently thick elements so that it is capable of developing a fully plastic stress distribution before buckling. The term plastic means stressed throughout to the yield stress. 10 Wednesday, October 20, 2021

For a compression member to be classified as compact its flanges must be continuously connected to its web or webs and the width thickness ratios of its compression elements may not be greater than the limiting ratios given in AISC Table B 4. 1 and reproduced in Table 3. 1. 2. Non-Compact Sections A non compact section is one for which the yield stress can be reached in some but not all of its compression elements just at the Wednesday, October 20, 11 buckling stage. 2021

In AISC Table B 4. 1, the non compact sections are defined as those sections which have width thickness ratios greater than but not greater than. Values of limiting b/t ratios ( ) are given in Table 3. 2. where the value of ‘kc’ is defined as under 12 Wednesday, October 20, 2021

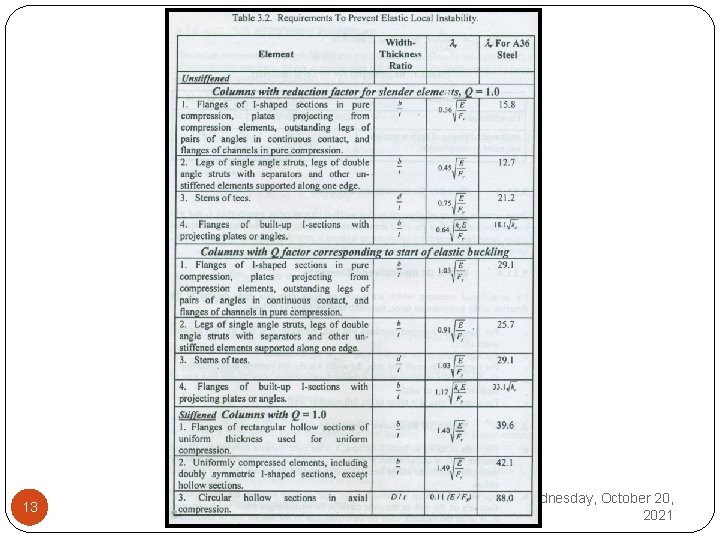
13 Wednesday, October 20, 2021

3. Slender Compression Sections These sections consist of elements having width thickness ratios greater than and will buckle elastically before the yield stress is reached in any part of the section. A special design procedure for slender compression sections is provided in Section E 7 of the AISC Specification. However, it will not be covered in detail here. 14 Wednesday, October 20, 2021

Width of Un-stiffened Elements For un stiffened elements, which are supported along only one edge parallel to the direction of the compression force, the width shall be taken as follows: a) For flanges of I shaped members and tees, the width b is half the full nominal width (bf/2). b) For legs of angles, the width b is the longer leg dimension. 15 Wednesday, October 20, 2021

c) For flanges of channels and zees, the width b is the full nominal dimension (bf). d) For plates, the width b is the distance from the free edge to the first row of fasteners or line of welds. e) For stems of tees, d is taken as the full nominal depth. 16 Wednesday, October 20, 2021

Width of Stiffened Elements a) For webs of rolled or formed sections, h is the clear distance between the flanges less the fillet or corner radius at each flange and hc is twice the distance from the centroidal axis to the inside face of the compression flange less the fillet or corner radius. b) For webs of built up sections, h is the clear distance between the inner lines of fasteners on the web or the clear distance between flanges when welds are used, Wednesday, October 20, 17 2021

hc is twice the distance from the centroidal axis to the nearest line of fasteners at the compression flange or the inside face of the compression flange when welds are used hp is twice the distance from the plastic neutral axis to the nearest lines of fasteners at the compression flange or the inside face of the compression flange when welds are used. 18 Wednesday, October 20, 2021

MODIFIED SLENDERNESS RATIO Snug Tight Connections Snug tight connection is defined as the type in which the plates involved in a connection are in firm contact with each other but without any defined contact prestress. It usually means the tightness obtained by the full effort of a man with a wrench or the tightness obtained after a few impacts of an impact wrench. Obviously there is some variation in the Wednesday, October 20, 19 2021 degree of tightness obtained under these

20 Snug Tight Connection Wednesday, October 20, 2021

The tightness is much lesser than tensioning of the high strength bolts. Turn-of-Nut Method: After the tightening of a nut to a snug fit, the specified pre tension in high strength bolts may be controlled by a predetermined rotation of the wrench. This procedure is called turn of nut method of fixing the bolts. 21 Wednesday, October 20, 2021

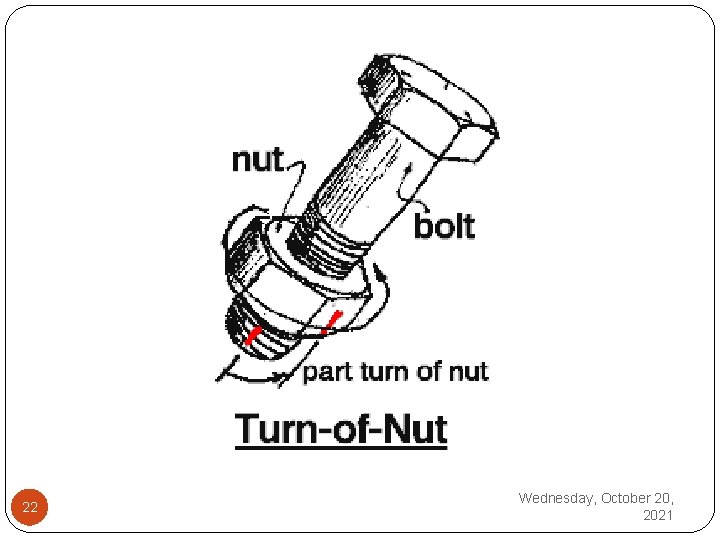
22 Wednesday, October 20, 2021

Air Impact Wrench 23 Wednesday, October 20, 2021

Hammer Impact Wrench 24 Wednesday, October 20, 2021

Electric Torque Wrench 25 Wednesday, October 20, 2021

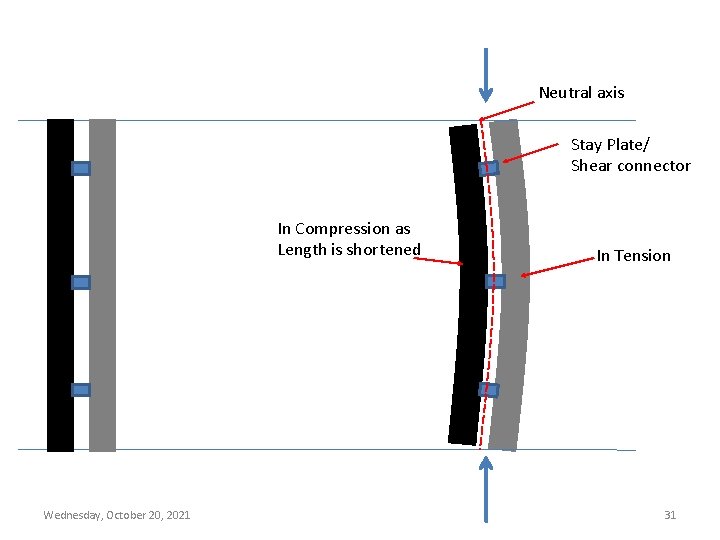
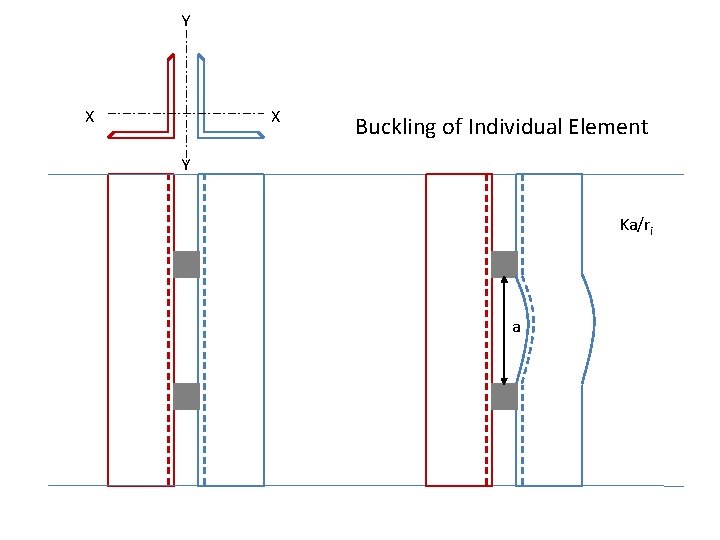
Shear Connections / Stay Plates Between Elements of a Built-Up Member Built up compression members composed of two or more hot rolled shapes shall be connected to one another at intervals by stay plates (shear connectors) such that the maximum slenderness ratio a/ri of individual element, between the fasteners, does not exceed the governing slenderness ratio of the built up member, that is, the greater value of (KL/r)x or (KL/r)y for the whole section. 26 Wednesday, October 20, 2021

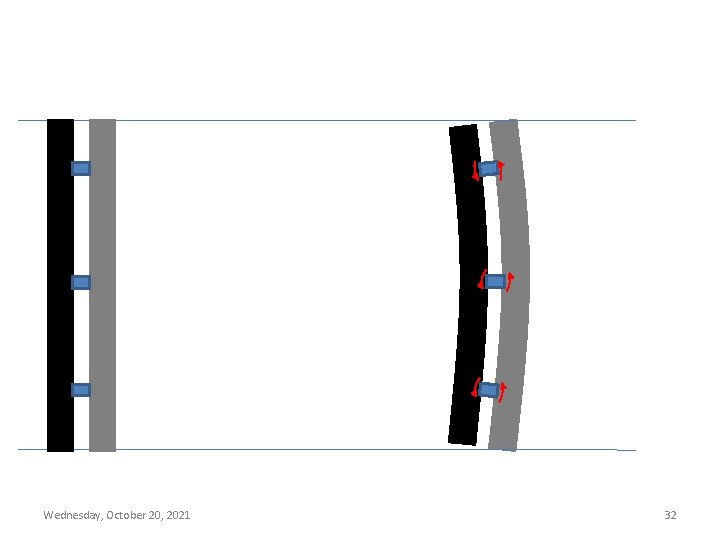
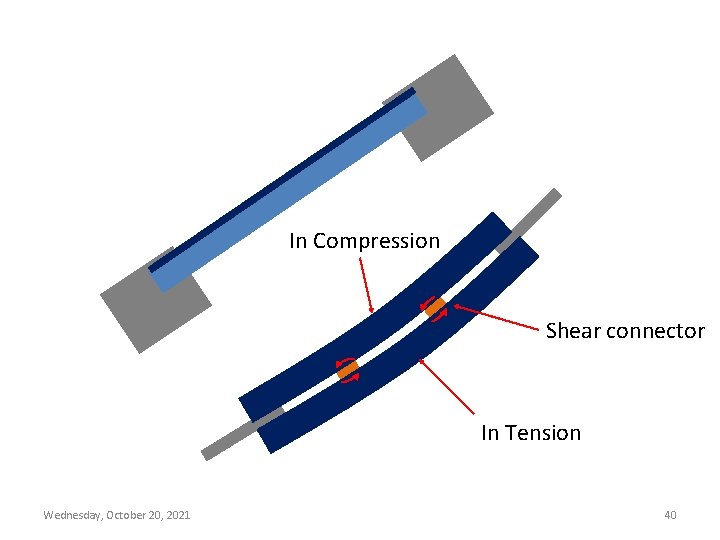
Shear connectors are also required to transfer shear between elements of a built up member that is produced due to buckling of the member. Following notation is used in further discussion of the effect of spacing of shear connectors: a ri 27 = distance between connectors = minimum radius of gyration of individual component Wednesday, October 20, 2021

rib = radius of gyration of individual component relative to its centroidal axis parallel to member axis of buckling = column slenderness of built up member as a whole = modified column slenderness of the built up member as a whole = separation ratio = h/(2 rib) h = distance between centroids of individual components perpendicular to the member Wednesday, October 20, 28 2021 axis of buckling

29

Wednesday, October 20, 2021 30

Neutral axis Stay Plate/ Shear connector In Compression as Length is shortened Wednesday, October 20, 2021 In Tension 31

Wednesday, October 20, 2021 32

Y X X Y Buckling about Y-axis

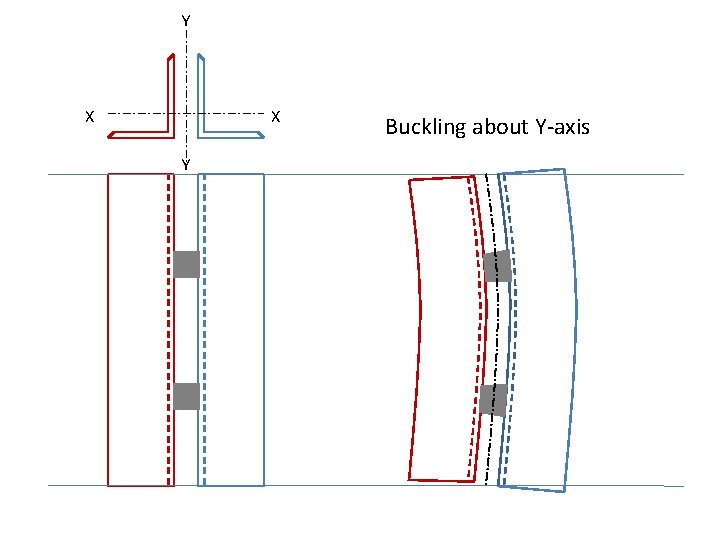
Y X X Y Buckling about Y-axis

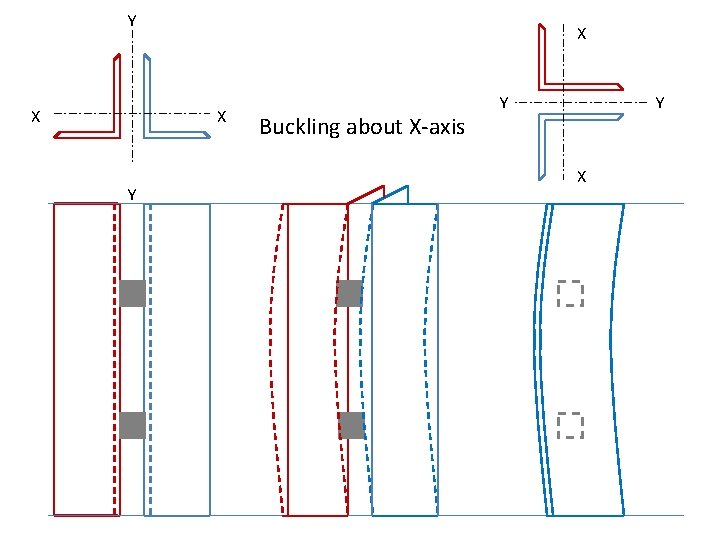
Y X X X Y Buckling about X-axis Y Y X

Wednesday, October 20, 2021 36

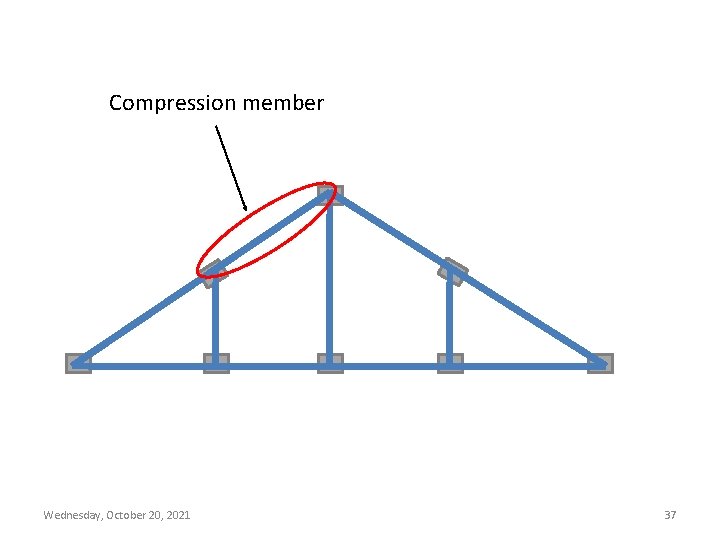
Compression member Wednesday, October 20, 2021 37

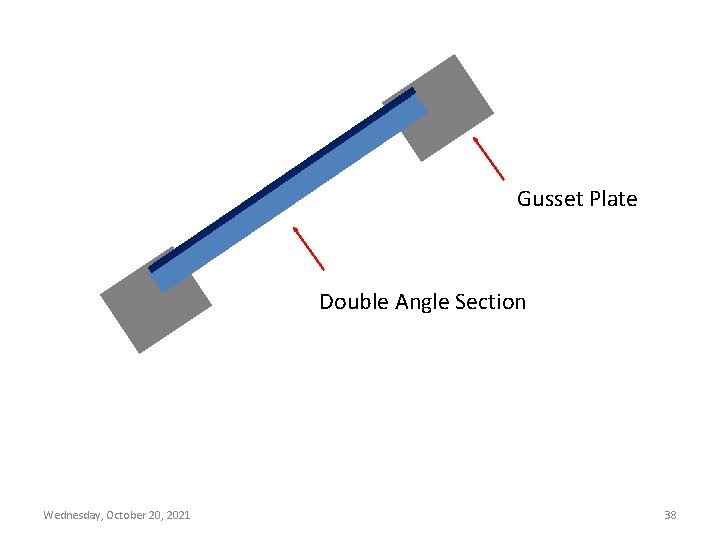
Gusset Plate Double Angle Section Wednesday, October 20, 2021 38

Wednesday, October 20, 2021 39

In Compression Shear connector In Tension Wednesday, October 20, 2021 40

Y X X Buckling of Individual Element Y Ka/ri a

Modified Slenderness Ratio Depending on Spacing of Stay Plates If the buckling mode of a built up compression member involves relative deformation that produces shear forces in the connectors between individual parts, the modified slenderness ratio is calculated as follows: a. for snug tight bolted connectors: 42 Wednesday, October 20, 2021

b. for welded connectors and for fully tightened bolted connectors as required for slip critical joints: 43 Wednesday, October 20, 2021

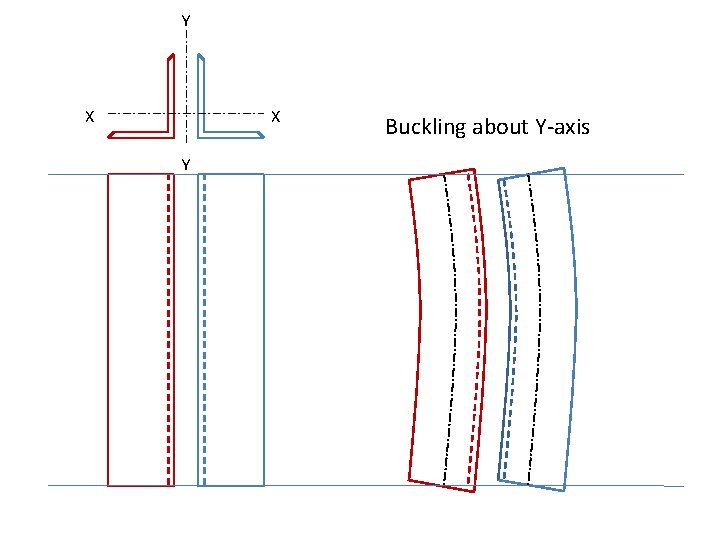
1. (KL/r)m should only be used if buckling occurs about such an axis such that the individual members elongate by different amounts. For example for double angles in Figure 3. 18, if buckling occurs about x axis, (KL/r)m is not evaluated as both the angles bend symmetrically without any shear between the two. However, if buckling occurs about y axis, one of the angle sections is elongated while the other is compressed producing shear Wednesday, October 20, 44 2021 between the two and consequently (KL/r) m

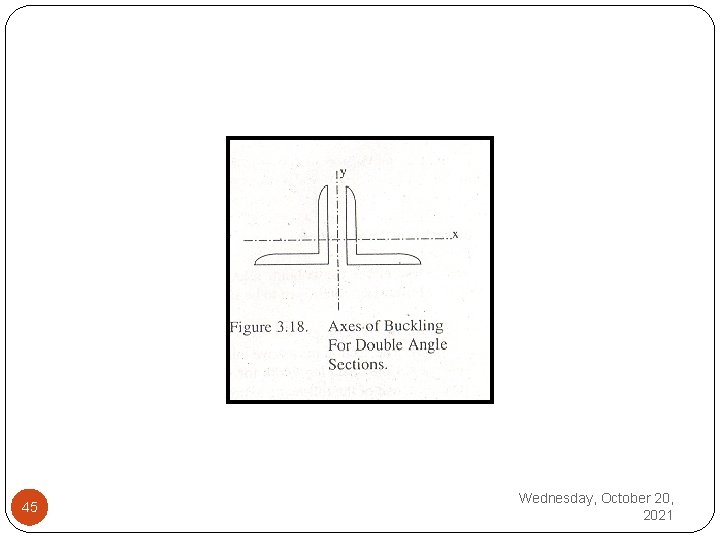
45 Wednesday, October 20, 2021

At the ends of built up compression members bearing on base plates or milled surfaces, all components in contact with one another shall be connected by a weld having a length not less than the maximum width of the member or by bolts spaced longitudinally not more than four diameters apart for a distance equal to 1. 5 times the maximum width of the member. 2. The 46 slenderness ratio of individual component between the connectors (Ka/ri) should not exceed 75% of the governing Wednesday, October 20, slenderness ratio of the built up member. 2021

CORRECTION FOR SINGLE ANGLES Single angle compression members may undergo torsional buckling at loads lower than the loads at which buckling may occur about x, y, or z axes. Hence, in order to closely estimate the capacity of equal leg angles or unequal leg angles connected through the longer leg, the slenderness ratio is to be modified as under: 47 Wednesday, October 20, 2021

a. PLANAR TRUSSES 1. when 0 ≤ L/rx ≤ 80, KL/r = 72 + 0. 75 L/rx 2. 48 Wednesday, October 20, 2021

In the above expressions, ‘rx’ is the radius of gyration about axis parallel to connected leg. However, to be on conservative side, critical slenderness ratio in this book is considered equal to larger of the above value and the slenderness ratio about the z axis. According to AISC E 5, the effects of eccentricity on single angle members may be neglected if same leg is loaded on both the ends, connections are by welding or minimum Wednesday, October 20, 49 of two bolts and when there are no transverse 2021

Detailed formulas for flexural torsional buckling, as given in AISC E 4, may also be employed to design such members. STRENGTH FOR FLEXURAL-TORSIONAL BUCKLING Torsional and flexural torsional buckling modes generally do not govern failure compared with the weak axis buckling mode. 50 Wednesday, October 20, 2021

These are critical for thin plate symmetric columns, un symmetric columns and columns having torsional unbraced lengths significantly larger than the weak axis lengths between braces. The following nomenclature is used to estimate the compressive strength for torsional and flexural torsional buckling of xo, yo = distance between shear centre and memberscentroid withoutinslender elements: the x and y directions, 51 respectively = Polar radius of gyration about the shear Wednesday, October 20, centre 2021

H = G = Shear modulus of elasticity, 77, 200 MPa ho = Distance between the flange centroids Cw = Warping constant, J = Torsional constant Fcrz = 52 Wednesday, October 20, 2021

Kz = Effective length factor for torsional buckling, may conservatively be taken equal to 1. 0, 0. 5 if both ends of the column provide warping restraint, 0. 7 if one end of the column provides warping restraint while other does not. Fex = Fey = 53 Wednesday, October 20, 2021

Fez = = Fcry for tees and double angles = Fcr calculated in the usual way for buckling about y axis, using KL/ry a. For Double Angles and Tee Shapes 54 Wednesday, October 20, 2021

b. For Doubly symmetric Shapes Fcr is then calculated by the usual formulas. c. For Singly symmetric Shapes about Y-axis Fcr is then calculated by the usual formulas. 55 Wednesday, October 20, 2021

d. For Un-symmetric Shapes Fe is calculated as the lowest root of the following cubic Fcr is then calculated by the usual formulas. 56 Wednesday, October 20, 2021

DESIGN FLOW CHART FOR COMPRESSION MEMBERS Inputs PD, PL, L, end conditions, etc Calculate Pu for the controlling/critical load combination. Also find the values of effective length factor Kx, Ky and Kz. Assume slenderness ratio (if column selection tables are not to be used): 57 Wednesday, October 20, 2021

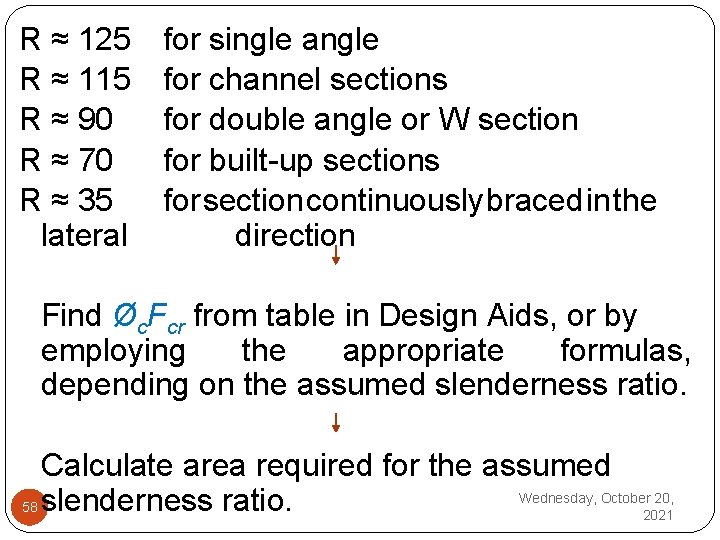
R ≈ 125 R ≈ 115 R ≈ 90 R ≈ 70 R ≈ 35 lateral for single angle for channel sections for double angle or W section for built up sections for section continuously braced in the direction Find Øc. Fcr from table in Design Aids, or by employing the appropriate formulas, depending on the assumed slenderness ratio. Calculate area required for the assumed Wednesday, October 20, 58 slenderness ratio. 2021

This may be different from the value for the actual slenderness ratio unknown at this stage and may be on the conservative or unsafe side of the actual value. Accordingly the selected area may be a little greater or lesser than the calculated required area. Selection of Trial Section Use either the column selection tables or Wednesday, October 20, adopt the trial and error procedure. Following 59 2021

a) Asel ≈ ± Areq mum ction The ust e ssible b) weight. edc) connections (bmin) is selected using one of the following expressions as applicable: i) iii) L/ 40 for L =2 to 3 m 3. 25 d + 26 > 50 mm for welded connections where d = diameter of rivets, may be assumed equal to 15 mm if not known. column Maximum section d) should of depth Wednesday, October 20, 60 2021

Calculate Critical Slenderness Ratio Find unsupported length in each direction Lux, Luy and Luz Calculate the radii of gyration (rx, ry, rz) or directly see their values from the properties of sections table. 61 Wednesday, October 20, 2021 R = maximum value out of the above

Select spacing of stay plates denoted by ‘a’, if used, such that: a/ri < 0. 75 R The selected spacing must be uniform and the stay plates should satisfy the modified slenderness ratio criteria. Smaller a may be selected to reduce the modified slenderness ratio, Rm. However, the number of stay plates in a member generally should not exceed 2 (or at the most 3). 62 Wednesday, October 20, 2021

Calculate the slenderness ratio modified for the position of stay plates (KL/r)m about the weak axis, in case the buckling of the built up section about this axis produces shear between the elements. Revise the critical slenderness ratio (R), if required. Perform Local Stability Check Examine λ = b/t ratios for stiffened and un stiffened elements of the section and the Wednesday, October 20, 63 following must be satisfied: 2021

Perform Maximum Slenderness Check R ≤ 200 OK otherwise revise by selection of another trial section. R greater than 200 may be allowed in special cases as per AISC recommendations. Øc To convert the result into k. N 64 Fe Wednesday, October 20, 2021

The additional factor of 0. 75 is used to exceed the recommended limit of 200. Find Øc. Fcr from table in Design Aids or using formulas 65 Wednesday, October 20, 2021

Perform Capacity Check Otherwise revise after fresh selection of section Check for Reversal of Stresses If Tu > 0, 66 check that Øt. Tn > Tu otherwise revise Wednesday, October 20, 2021

Check for Loading Cycles Assume that loading cycles are lesser than 20, 000 for ordinary buildings. Design Stay Plates or Lacing Design Connections 67 Wednesday, October 20, 2021

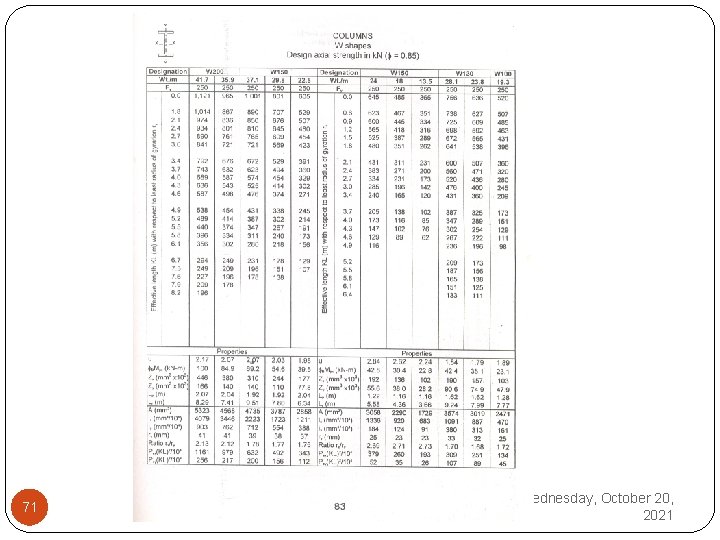
ALTERNATE AND EASY METHOD TO SELECT TRIAL SECTION W-Section Load carrying capacities (Øc. Pn) for various W sections against the values of effective lengths with respect to least radius of gyration are tabulated in Design Aids. Corresponding to the value of effective length Ky. Luy, a section may be selected when the tabulated (Øc. Pn) becomes just greater than Pu while moving from left to right. 68 Few sections with different depths may be Wednesday, October 20, 2021

To check stability of the section about the x axis, Kx. Lx is converted into an equivalent Ky. Ly by using the following expression: where rx/ry is used for the previously selected section. The ratio rx/ry included in these tables provides a convenient method for investigating the strength of a column with respect to its major axis. Section is selected/revised for longer of the two lengths Ky. Ly and (Ky. Ly)eq. 69 Wednesday, October 20, 2021

Procedure 1. Find maximum values of Kx. Lx and Ky. Ly. 2. Select section against Ky. Ly according to the loads starting from W 360 side and moving downward by weight. 3. Find rx/ry for the selected section and calculate equivalent Ky. Ly as Kx. Lx/(rx/ry). 4. Re enter the table for greater value out of Ky. Ly and (Ky. Ly)eq. 5. Revise the section if necessary. 70 Wednesday, October 20, 2021

71 Wednesday, October 20, 2021

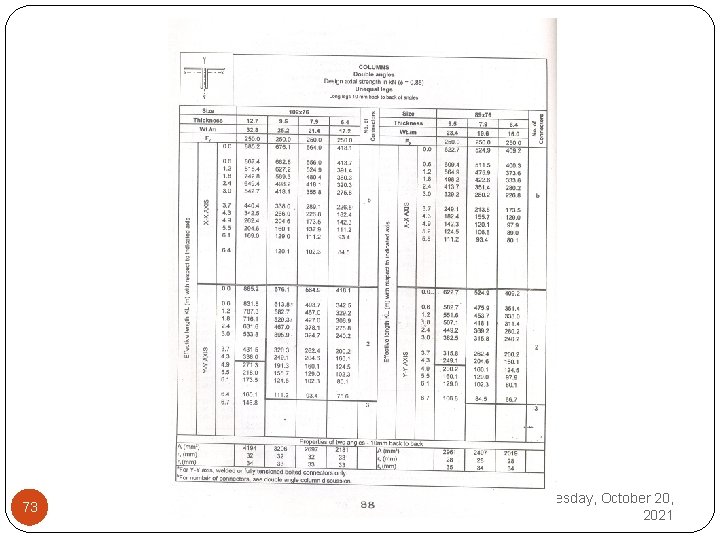
Double Angle Section Column selection tables are also given for the double angle sections with 10 mm gusset plate in Design Aids, using fully tightened stay plates. Only difference in this case is that the load carrying capacities (Øc. Pn) are listed both for Kx. Lx and Ky. Ly. While selecting section, (Øc. Pn) for both Kx. Lx and Ky. Ly should individually be greater than P u. 72 Wednesday, October 20, 2021 After the selection of the section, all the

73 Wednesday, October 20, 2021