Design of Asynchronous State Machine Design Steps 1




- Slides: 7

Design of Asynchronous State Machine Design Steps: 1. Prmitive State Diagram. 2. Primitive Flow Table. 3. Redution of Primitive flow Table. 4. Merging. 5. Merger Diagram. 6. Merged Flow Table. 7. Adjacency Sets. 8. Assignments Flow Table. 9. Logic Circuit. Example 1: Design an asynchronous sequential logic circuit which has two inputs (X 1&X 2) and one output (Z). The output (Z) must go to (1) at the end of the input sequence (00, 01, 11). This output must be maintained (unchanged) for all input changes until the sequence (11, 10, 00) occurs, then the output must go to zero(0). Solution: - Asynchronous S. M. S X 1 X 2= 00, 01, 11 Z=1 X 1 X 2= 11, 10, 00 Z=0 63

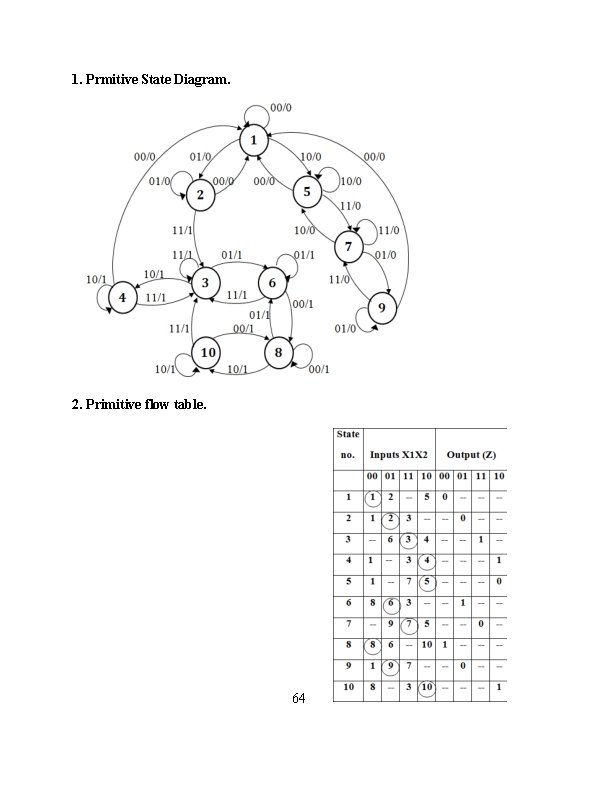
1. Prmitive State Diagram. 2. Primitive flow table. 64

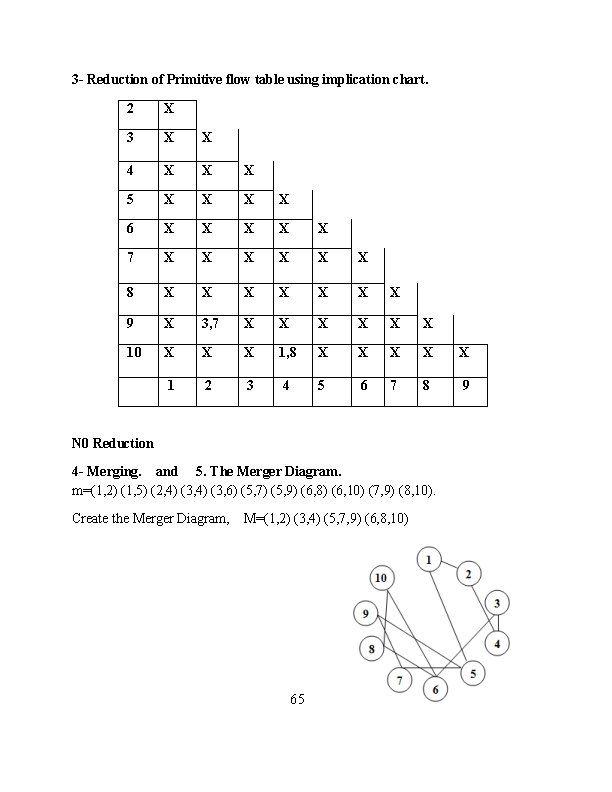
3 - Reduction of Primitive flow table using implication chart. 2 X 3 X X 4 X X X 5 X X 6 X X X 7 X X X 8 X X X X 9 X 3, 7 X X X 10 X X X 1, 8 X X X 1 2 3 4 5 6 7 8 9 N 0 Reduction 4 - Merging. and 5. The Merger Diagram. m=(1, 2) (1, 5) (2, 4) (3, 6) (5, 7) (5, 9) (6, 8) (6, 10) (7, 9) (8, 10). Create the Merger Diagram, M=(1, 2) (3, 4) (5, 7, 9) (6, 8, 10) 65

6. Merged Flow Table. A B 00 1 1 01 2 6 11 3 3 10 5 4 Z o/p 0 1 C D 1 8 9 6 7 3 5 10 0 1 7. Adjacency Sets. X 1 X 2=00 X 1 X 2=01 X 1 X 2=10 (a, b, c); (b, d); (a, c) Y 2 Y 1 0 A B 1 C D (Row Transition Map) Note: The stable state take the code of the same row and the unstable state take the code of it's row where they are stable. 8. Assignments Flow Table. 66 Inputs X 1 X 2 00 01 11 10 Z y 1 y 2 y 1 y 2 o/p

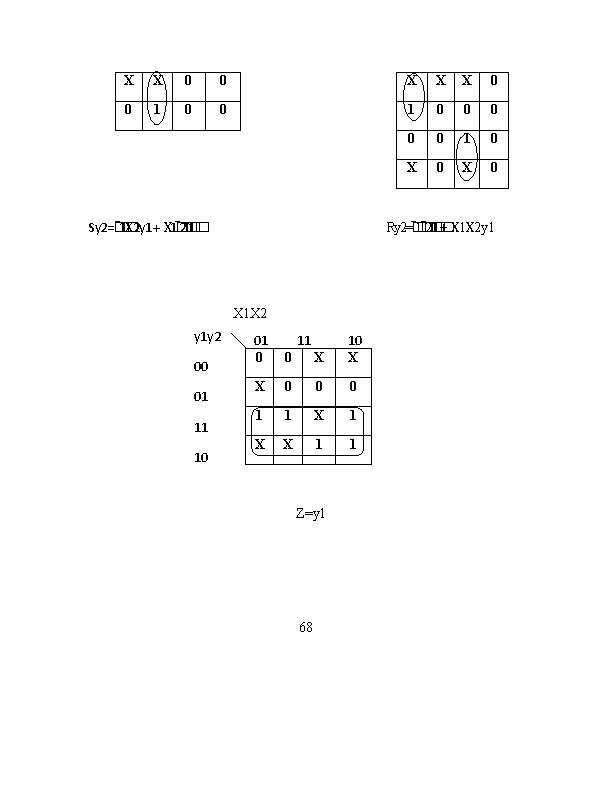
a 00 b 10 c 01 d 11 00 00 00 11 01 11 10 10 01 11 0 1 "Assigned Flow Table" Circuit Relaization: Design the circuit using the S-R flip-flops. y 1 y 2 00 X 1 X 2 01 11 0 0 10 1 0 0 0 0 11 X X 10 0 X X X y 1 y 2 X 1 X 2 01 11 10 X X X X X 0 0 1 0 00 01 11 10 Sy 1=X 1 X 2�� �� Ry 1=�� 1 �� 2 67 y 1 y 2 00 01 X 1 X 2 11 01 0 0 X X 10 1 y 1 y 2 X 01 00 11 11 10 10 X 1 X 2 01 11 10

X X 0 0 X X X 0 0 1 0 X 0 1 X 2 y 1 + X 1�� 2�� Sy 2=�� 1 Ry 2=�� 1 �� 2 �� 1+ X 1 X 2 y 1 X 1 X 2 y 1 y 2 00 01 11 10 01 0 11 0 X 10 X X 0 0 0 1 1 X X 1 1 Z=y 1 68
