Design of an ODE Solver Environment System of

Design of an ODE Solver Environment

System of ODEs Consider the system of ODEs: Typically solved by forward Euler or 4 th order Runge-Kutta

Traditional Approach Traditionally solved by library routines: SUBROUTINE RK 4 (Y, T, F, WORK 1, N, TSTEP, TOL 1, TOL 2, …) Y: current value of y T: current value for time t F: external function defining f WORK 1: work array N: length of array TSTEP: time step value TOL 1, TOL 2: algorithmic parameters

Model Problem Define and you get:

Traditional Interface That is, the function F has the following interface: SUBROUTINE F (YDOT, Y, T, C 1, C 2, C 3, C 4, OMEGA) NB! Problem-dependent interface!! Solvers like RK 4 wants: SUBROUTINE F (YDOT, Y, T) (Bad) Solution: COMMON block (global data)

The Object-Oriented Way • User program can access base class (solver unknown) • Class hierarchy of solvers • Embedding of problem-specific parameters • Uniform interface for function f

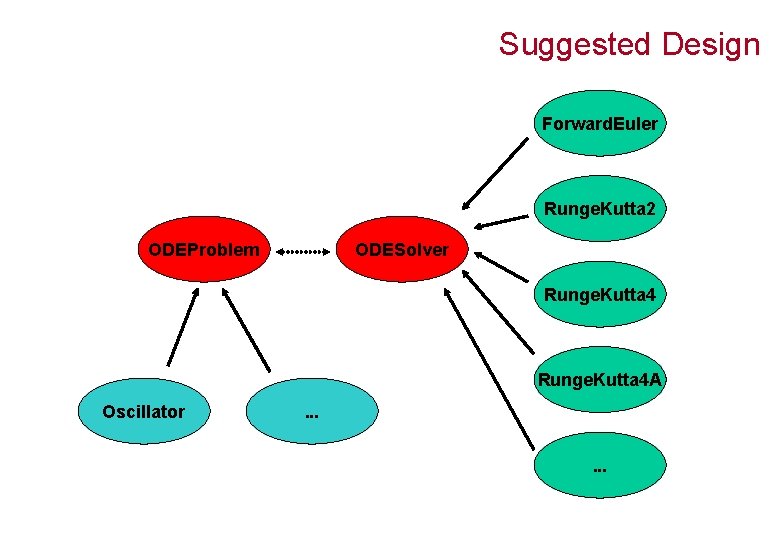
Suggested Design Forward. Euler Runge. Kutta 2 ODEProblem ODESolver Runge. Kutta 4 A Oscillator . . .

Class ODESolver class ODESolver { protected: // members only visible in subclasses ODEProblem* eqdef; // definition of the ODE in user's class public: // members visible also outside the class ODESolver (ODEProblem* eqdef_) { eqdef = eqdef_; } virtual ~ODESolver () {} // always needed, does nothing here. . . virtual void init(); // initialize solver data structures virtual void advance (Vec(real)& y, real& t, real& dt); };

Class ODEProblem class ODEProblem { protected: ODESolver* solver; // some ODE solver Vec(real) y, y 0; // solution (y) and initial condition (y 0) real t, dt, T; // time loop parameters public: ODEProblem () {} virtual ~ODEProblem (); virtual void time. Loop (); virtual void equation (Vec(real)& f, const Vec(real)& y, real t); virtual int size (); // no of equations in the ODE system virtual void scan (); virtual void print (Os os); };

The Time Loop void ODEProblem: : time. Loop () { Os outfile (aform("%s. y", casename. c_str()), NEWFILE); t = 0; y = y 0; outfile << t << " "; y. print(outfile); outfile << 'n'; while (t <= T) { solver->advance (y, t, dt); // update y, t, and dt outfile << t << " "; y. print(outfile); outfile << 'n'; } }

Class Oscillator class Oscillator : public ODEProblem { protected: real c 1, c 2, c 3, c 4, omega; // problem dependent paramters public: Oscillator () {} virtual void equation (Vec(real)& f, const Vec(real)& y, real t); virtual int size () { return 2; } // 2 x 2 system of ODEs virtual void scan (); virtual void print (Os os); };

Defining the ODE void Oscillator: : equation (Vec(real)& f, const Vec(real)& y_, real t_) { f(1) = y_(2); f(2) = -c 1*(y_(2)+c 2*y_(2)*abs(y_(2))) - c 3*(y_(1)+c 4*pow 3(y_(1))) + sin(omega*t_); }

Class Forward. Euler class Forward. Euler : public ODESolver { Vec(real) scratch 1; // needed in the algorithm public: Forward. Euler (ODEProblem* eqdef_); virtual void init (); // for allocating scratch 1 virtual void advance (Vec(real)& y, real& t, real& dt); };

Stepping the Solver void Forward. Euler: : advance (Vec(real)& y, real& t, real& dt) { eqdef->equation (scratch 1, y, t); // evaluate scratch 1 (as f) const int n = y. size(); for (int i = 1; i <= n; i++) y(i) += dt * scratch 1(i); t += dt; }

Parameter Classes class ODESolver_prm { public: String method; // name of subclass in ODESolver hierarchy ODEProblem* problem; // pointer to user's problem class ODESolver* create (); // create correct subclass of ODESolver }; ODESolver* ODESolver_prm: : create () { ODESolver* ptr = NULL; if (method == "Forward. Euler") ptr = new Forward. Euler (problem); else if (method == "Runge. Kutta 4") ptr = new Runge. Kutta 4 (problem); else error. FP("ODESolver_prm: : create", "Method "%s" is not available", method. c_str()); return ptr; }

Problem Input void ODEProblem: : scan () { const int n = size(); // call size in actual subclass y. redim(n); y 0. redim(n); s_o << "Give " << n << " initial conditions: "; y 0. scan(s_i); s_o << "Give time step: "; s_i >> dt; s_o << "Give final time T: "; s_i >> T; ODESolver_prm solver_prm; s_o << "Give name of ODE solver: "; s_i >> solver_prm. method; solver_prm. problem = this; solver = solver_prm. create(); solver->init(); // more reading in user's subclass }

Problem Input void Oscillator: : scan () { // first we need to do everything that ODEProblem: : scan does: ODEProblem: : scan(); // additional reading here: s_o << "Give c 1, c 2, c 3, c 4, and omega: "; s_i >> c 1 >> c 2 >> c 3 >> c 4 >> omega; print(s_o); // convenient check for the user }

The Main Program int main (int argc, const char* argv[]) { init. Diffpack (argc, argv); Oscillator problem; problem. scan(); // read input data and initialize problem. time. Loop(); // solve problem return 0; }

What Has Been Gained? • Some “disturbance” of basic numerics • Flexible library • Faster to define problem (f) than hardcoding solver • Simple example, ideas transfer to very complicated scenarios

Exercise: Extending the ODE Environment Use the ODE environment to solve the problem u’(t) = -u(t) u(0) = 1 The analytical solution to this problem is u(t)=e-t.