Design of a robust multimicrophon noise reduction algorithm

Design of a robust multi-microphon noise reduction algorithm for hearin instruments 1 1 2 Simon Doclo , Ann Spriet 1, 2, Marc Moonen , Jan Wouters 1 Dept. of Electrical Engineering (ESAT-SCD), KU Leuven, Belgium 2 Laboratory for Exp. ORL, KU Leuven, Belgium MTNS-2004, 08. 07. 2004

Overview • Problem statement: hearing in background noise • Adaptive beamforming: GSC o not robust against model errors • Design of robust noise reduction algorithm o robust fixed spatial pre-processor o robust adaptive stage • Low-cost implementation of adaptive stage • Experimental results + demo • Conclusions 2

Problem statement § Introduction -Problem statement -State-of-the-art -GSC § Robust spatial pre-processor § Adaptive stage § Conclusions • Hearing problems effect more than 10% of population hearing aids and cochlear implants • Digital hearing instruments allow for advanced signal processing, resulting in improved speech understanding • Major problem: (directional) hearing in background noise o o reduction of noise wrt useful speech signal multiple microphones + DSP current systems: simple fixed and adaptive beamforming robustness important due to small inter-microphone distance design of robust multi-microphone noise reduction scheme 3

State-of-the-art noise reduction § Introduction -Problem statement -State-of-the-art -GSC § Robust spatial • Single-microphone techniques: o spectral subtraction, Kalman filter, subspace-based o only temporal and spectral information limited performance pre-processor § Adaptive stage § Conclusions • Multi-microphone techniques: o exploit spatial information o Fixed beamforming: fixed directivity pattern o Adaptive beamforming (e. g. GSC) : adapt to different acoustic environments improved performance Sensitive to a-priori assumptions o Multi-channel Wiener filtering (MWF): MMSE estimate of speech component in microphones improved robustness Robust scheme, encompassing both GSC and MWF 4

Adaptive beamforming: GSC Adaptive Noise Canceller § Introduction (adaptation during noise) -Problem statement -State-of-the-art -GSC S Spatial pre-processing Speech reference Fixed beamformer A(z) § Robust spatial pre-processor Blocking matrix B(z) § Adaptive stage § Conclusions Noise references • Fixed spatial pre-processor: o o • Fixed beamformer creates speech reference Blocking matrix creates noise references Adaptive noise canceller: o Standard GSC minimises output noise power 5

Robustness against model errors § Introduction -Problem statement -State-of-the-art -GSC § Robust spatial • Spatial pre-processor and adaptive stage rely on assumptions (e. g. no microphone mismatch, no reverberation, …) • In practice, these assumptions are often not satisfied pre-processor o Distortion of speech component in speech reference § Adaptive stage o Leakage of speech into noise references, i. e. Speech component in output signal gets distorted § Conclusions • Design of robust noise reduction algorithm: 1. Design of robust spatial pre-processor (fixed beamformer) 2. Design of robust adaptive stage Limit distortion both in and 6

Robust spatial pre-processor § Introduction • Small deviations from assumed microphone characteristics (gain, phase, position) large deviations from desired directivity pattern, especially for small-size microphone arrays • In practice, microphone characteristics are never exactly known § Robust spatial pre-processor § Adaptive stage Measurement or calibration procedure § Conclusions Incorporate specific (random) deviations in design • Consider all feasible microphone characteristics and optimise o average performance using probability as weight – requires statistical knowledge about probability density functions – cost function J : least-squares, eigenfilter, non-linear o worst-case performance minimax optimisation problem 7

Simulations § Introduction • N=3, positions: [-0. 01 0 0. 015] m, L=20, fs=8 k. Hz § Robust spatial • Passband = 0 o-60 o, 300 -4000 Hz (endfire) Stopband = 80 o-180 o, 300 -4000 Hz § Adaptive stage • Robust design - average performance: Uniform pdf = gain (0. 85 -1. 15) and phase (-5 o-10 o) • Deviation = [0. 9 1. 1 1. 05] and [5 o -2 o 5 o] • Non-linear design procedure (only amplitude, no phase) pre-processor § Conclusions 8

Simulations Non-robust design Robust design § Introduction Deviations (gain/phase) d. B Angle (deg) Frequency (Hz) d. B § Conclusions d. B § Adaptive stage No deviations pre-processor d. B § Robust spatial 9

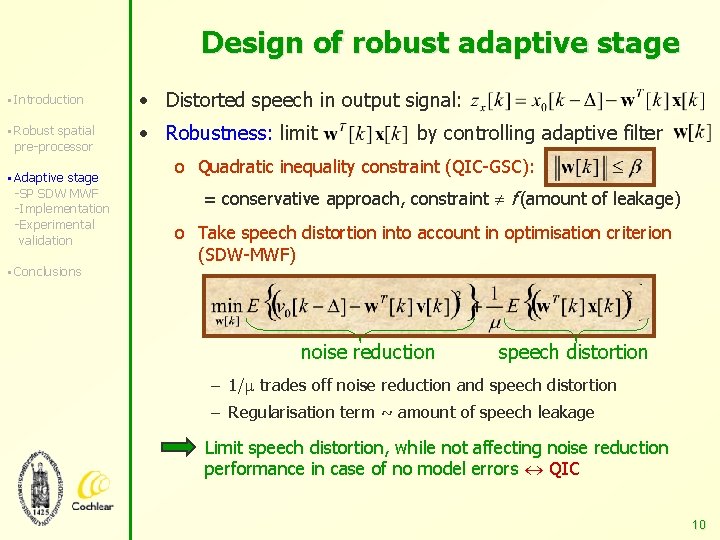
Design of robust adaptive stage § Introduction • Distorted speech in output signal: § Robust spatial • Robustness: limit pre-processor § Adaptive stage -SP SDW MWF -Implementation -Experimental validation § Conclusions by controlling adaptive filter o Quadratic inequality constraint (QIC-GSC): = conservative approach, constraint f (amount of leakage) o Take speech distortion into account in optimisation criterion (SDW-MWF) noise reduction speech distortion – 1/ trades off noise reduction and speech distortion – Regularisation term ~ amount of speech leakage Limit speech distortion, while not affecting noise reduction performance in case of no model errors QIC 10

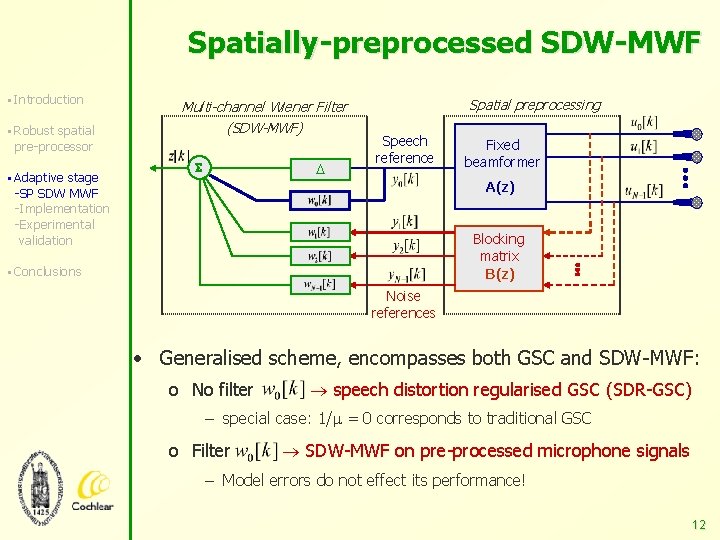
Spatially-preprocessed SDW-MWF § Introduction § Robust spatial Multi-channel Wiener Filter (SDW-MWF) pre-processor § Adaptive stage S Spatial preprocessing Speech reference Fixed beamformer A(z) -SP SDW MWF -Implementation -Experimental validation Blocking matrix B(z) § Conclusions Noise references • Generalised scheme, encompasses both GSC and SDW-MWF: o No filter speech distortion regularised GSC (SDR-GSC) – special case: 1/ = 0 corresponds to traditional GSC o Filter SDW-MWF on pre-processed microphone signals – Model errors do not effect its performance! 12

Low-cost implementation § Introduction § Robust spatial • Stochastic gradient algorithm in time-domain: o Cost function pre-processor § Adaptive stage -SP SDW MWF -Implementation -Experimental validation results in LMS-based updating formula § Conclusions Classical GSC regularisation term o Approximation of regularisation term in TD using data buffers o Allows transition to classical LMS-based GSC by tuning some parameters (1/ , w 0) • Complexity reduction in frequency-domain: o Block-based implementation: fast convolution and correlation o Approximation of regularisation term in FD allows to replace data buffers by correlation matrices 13

Experimental validation (1) § Introduction § Robust spatial pre-processor § Adaptive stage -SP SDW MWF -Implementation -Experimental validation § Conclusions • Set-up: o 3 -mic BTE on dummy head (d = 1 cm, 1. 5 cm) o Speech source in front of dummy head (0 ) o 5 speech-like noise sources: 75 , 120 , 180 , 240 , 285 o Microphone gain mismatch at 2 nd microphone • Performance measures: o Intelligibility-weighted signal-to-noise ratio – Ii = band importance of i th one-third octave band – SNRi = signal-to-noise ratio in i th one-third octave band o Intelligibility-weighted spectral distortion – SDi = average spectral distortion in i th one-third octave band (Power Transfer Function for speech component) 15

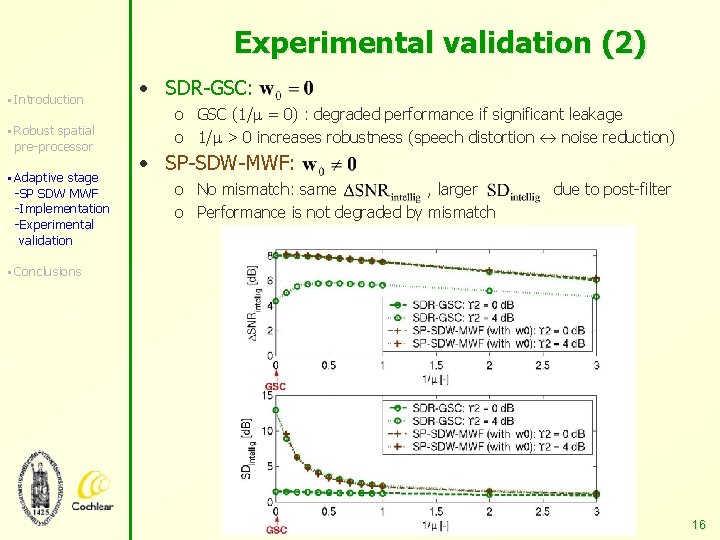
Experimental validation (2) § Introduction § Robust spatial pre-processor § Adaptive stage -SP SDW MWF -Implementation -Experimental validation • SDR-GSC: o GSC (1/ = 0) : degraded performance if significant leakage o 1/ > 0 increases robustness (speech distortion noise reduction) • SP-SDW-MWF: o No mismatch: same , larger o Performance is not degraded by mismatch due to post-filter § Conclusions 16

Audio demonstration § Introduction Algorithm No deviation Deviation (4 d. B) § Robust spatial pre-processor Noisy microphone signal § Adaptive stage -SP SDW MWF -Implementation -Experimental validation § Conclusions Speech reference Noise reference Output GSC Output SDR-GSC Output SP-SDW-MWF 18

Conclusions § Introduction § Robust spatial pre-processor § Adaptive stage § Conclusions • Design of robust multimicrophone noise reduction algorithm: o Design of robust fixed spatial preprocessor need for statistical information about microphones o Design of robust adaptive stage take speech distortion into account in cost function Spatially pre-processed SDW Multichannel Wiener Filter • SP-SDW-MWF encompasses GSC and MWF as special cases • Experimental results: o SP-SDW-MWF achieves better noise reduction than QIC-GSC, for a given maximum speech distortion level o Filter w 0 improves performance in presence of model errors • Implementation: stochastic gradient algorithms available at affordable complexity and memory 19