Design and Implementation of a HighSpeed LowPower VLSI

Design and Implementation of a High-Speed, Low-Power VLSI Chip for the DCT Transform Project Advisor: Professor A. Doboli Participates: Tak Yuen Lam, Kit Lam, Wei Kit Ng, Ying Lam

Back Ground l The DCT application can have many purposes: – Filtering – Teleconferencing – high-definition television (HDTV) – speech coding, image coding – data compression, and more.

Back Ground l All of these use DCT algorithm for compression and/or filtering purposes. The DCT has – energy packing capabilities – approaches the statistically optimal transform in de-correlating a signal. – It was implemented with discrete components in a chip.

Goal. • Implementation of a VLSI chip with: -high speed -low power • compute the 2 -D Discrete Cosine Transform (DCT) function of an 8 x 8 element matrix is presented.

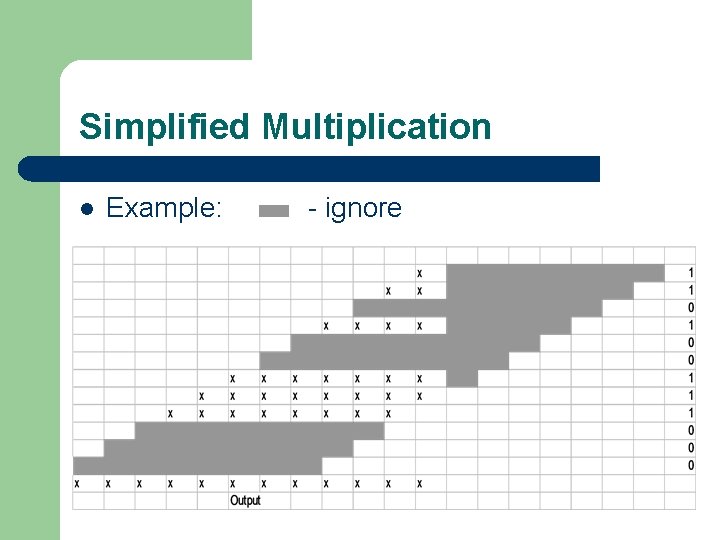
Goal • Save Power Consumption during Computing Operation in the chip: -Specially design multiplier with less computation. -Less switching -Simplify of the equations. • High Speed Processing: - using pipeline technology. - Ignore zero’s in the multiplier.

Basic Formula l Forward DCT: l Inverse DCT:

Basic Formula l C(u) = , C(v) = l C(u) = , C(v) = l through N-1; l N = 4, 8, or 16 for u, v = 0 for u, v = 1

1 -D DCT Matrix

Simplification:

The following equations are derived from the matrix above

Simplified Equations • Y(0) = c 4[j + k+l+m] • Y(2) = c 2[j-k] + c 6[m-l] • Y(4) = -c 4[j+k+l+m] • Y(6) = c 6[j-k] –c 2[m-l] • Y(1) = e + f + h + [c+c 3 -c 5 -c 7]a • Y(3) = e + g + I + [c 1+c 3+c 5 -c 7]b • Y(5) = e + g + h + [c 1+c 3 -c 5+c 7]c • Y(7) = e + f + I + [-c 1+c 3+c 5 -c 7]d

Simplified Equations • • • a = x 0–x 7; b= x 1 -x 6; c = x 2–x 5; d = x 3 -x 4 j = x 0+x 7; k = x 1+x 6; l = x 2+x 5; m= x 3+x 4 e = c 3[a+b+c+d] f=[c 7 -c 3][a-d] g=[-c 1 -c 3][b+c] h=[c 5 -c 3][a+c] I=[-c 5 -c 3][b+d]

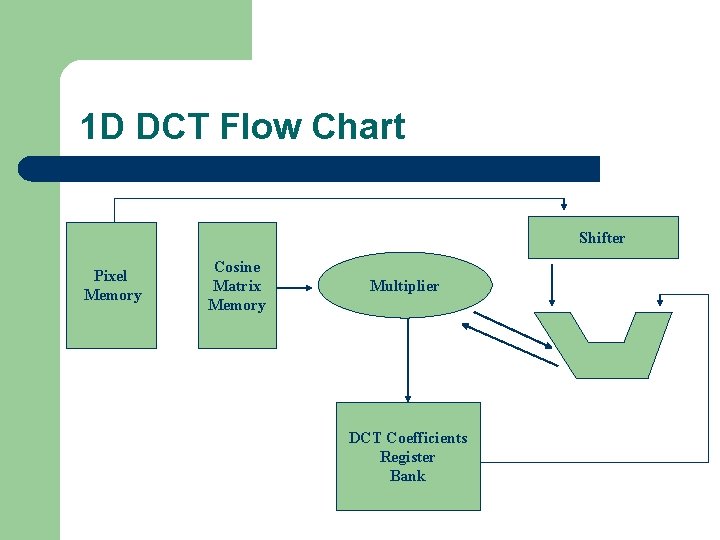
1 D DCT Flow Chart Shifter Pixel Memory Cosine Matrix Memory Multiplier DCT Coefficients Register Bank

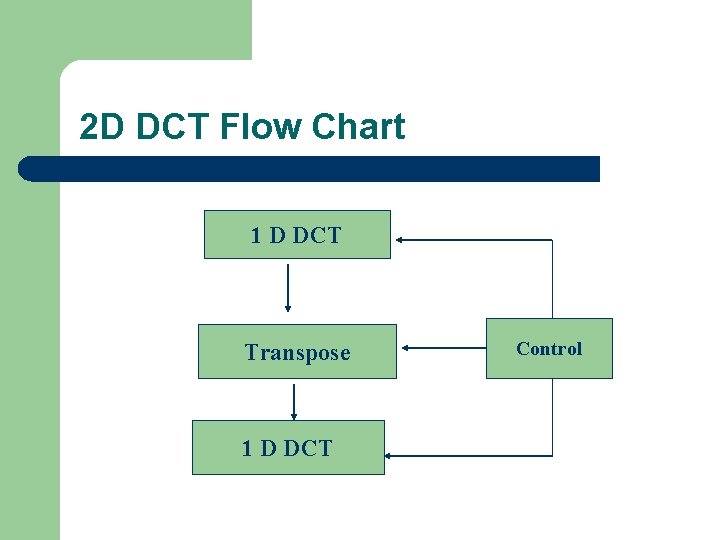
2 D DCT Flow Chart 1 D DCT Transpose 1 D DCT Control

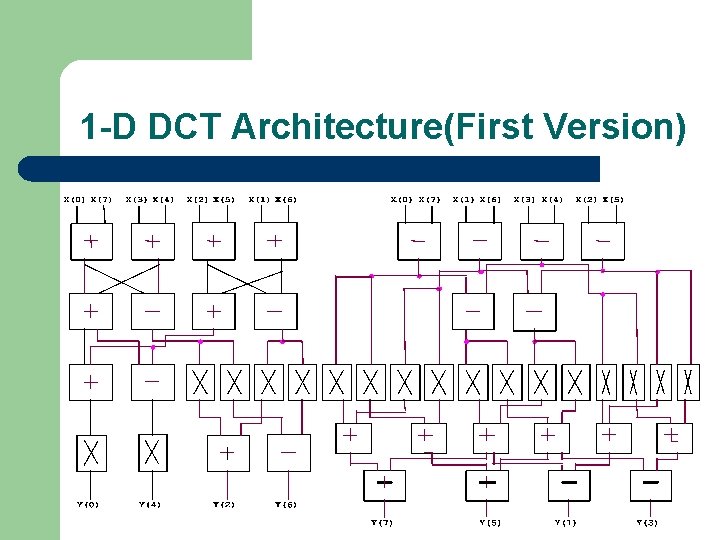
1 -D DCT Architecture(First Version)

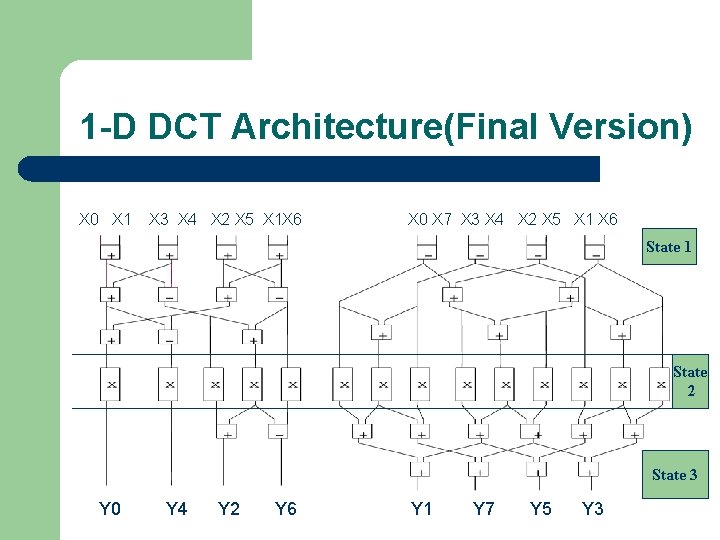
1 -D DCT Architecture(Final Version) X 0 X 1 X 3 X 4 X 2 X 5 X 1 X 6 X 0 X 7 X 3 X 4 X 2 X 5 X 1 X 6 State 1 State 2 State 3 Y 0 Y 4 Y 2 Y 6 Y 1 Y 7 Y 5 Y 3

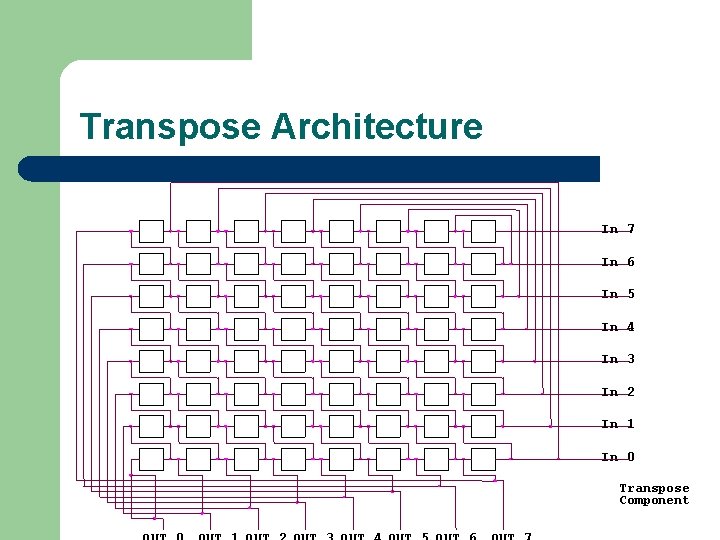
Transpose Architecture In 7 In 6 In 5 In 4 In 3 In 2 In 1 In 0 Transpose Component

Hardware: Fuller Adder

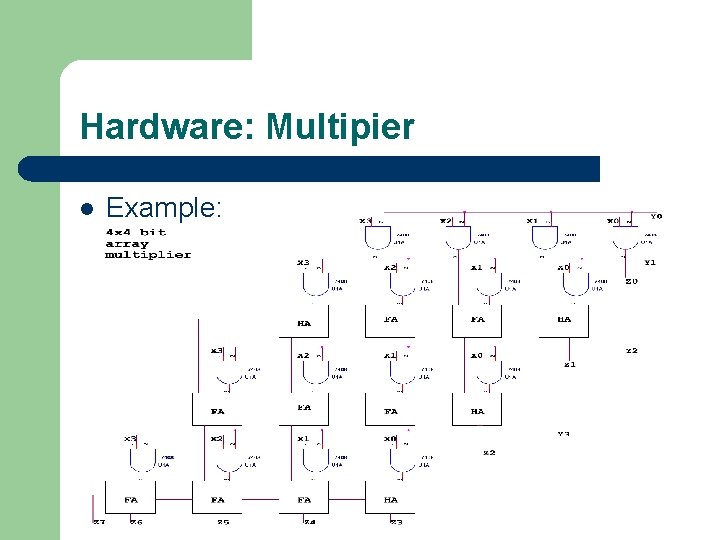
Hardware: Multipier l Example:

Simplified Multiplication l Example: - ignore

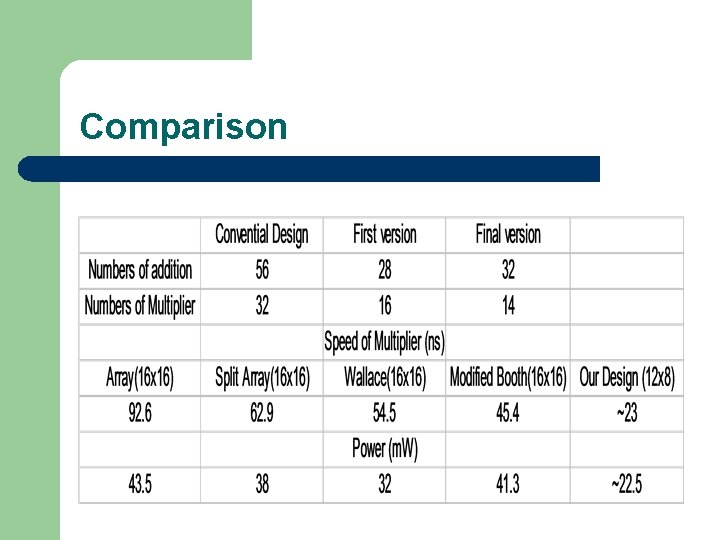
Comparison

VLSI: Full Adder (from Library)

VLSI: Multiplier

Multiplier Simulation

VLSI: 1 bit Transpose

VLSI: 8 x 8 Transpose

Transpose Simulation

VLSI: 1 D DCT Part One

1 D DCT Part One Simulation

VLSI: 1 D DCT Part Two

1 D DCT Part two Simulation

Java simulation l Java Code: public void transform() { g = new int[8][8]; for ( int i = 0; i < 8; i++ ) { for ( int j = 0; j < 8; j++ ) { double ge = 0. 0; for ( int x = 0; x < 8; x++ ) { for ( int y = 0; y < 8; y++ ) { double cg 1 = (2. 0*(double)x+1. 0)*(double)i*Math. PI/16. 0; double cg 2 = (2. 0*(double)y+1. 0)*(double)j*Math. PI/16. 0; ge += ((double)f[x][y]) * Math. cos(cg 1) * Math. cos(cg 2); } } double ci = ((i==0)? 1. 0/Math. sqrt(2. 0): 1. 0); double cj = ((j==0)? 1. 0/Math. sqrt(2. 0): 1. 0); ge *= ci * cj * 0. 25; g[i][j] = (int)Math. round(ge); } } }

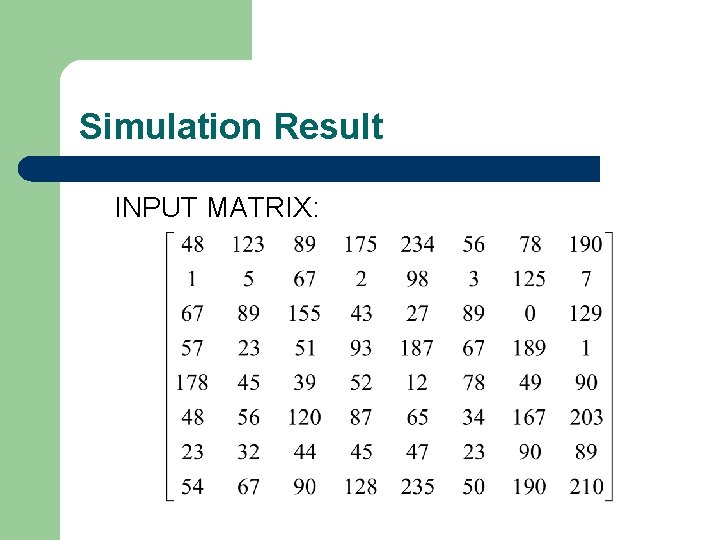
Simulation Result INPUT MATRIX:

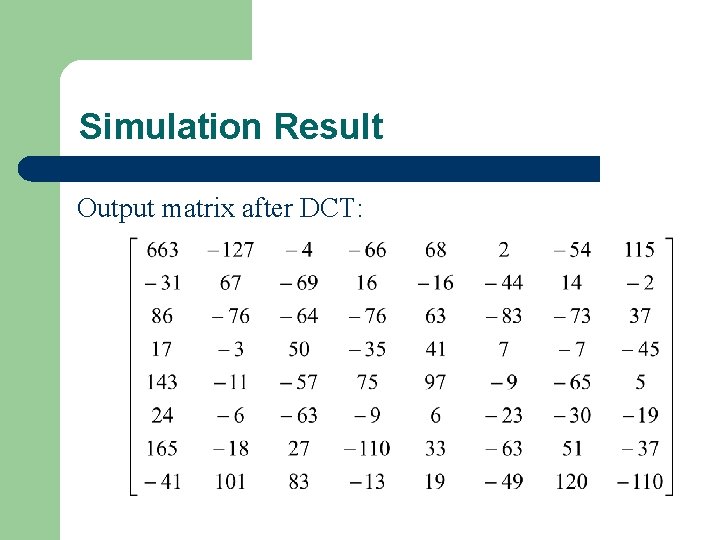
Simulation Result Output matrix after DCT: