Design and Communication Graphics Principles of Transformation Geometry

Design and Communication Graphics Principles of Transformation Geometry and their applications

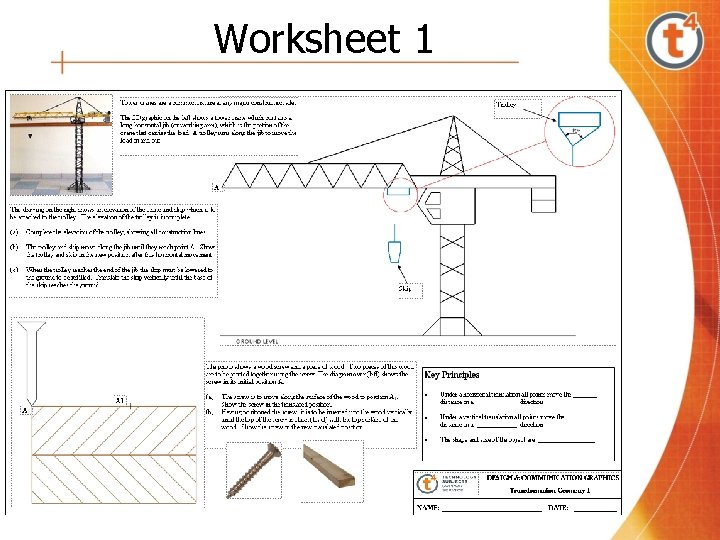
Worksheet 1

Worksheets 1, 2 & 4 Having completed these worksheets, the students should be able to • Construct the images of plane figures under translations • Identify that the shape and size of objects remain the same under a translation • Translate figures specific distances in horizontal, vertical and inclined directions • Construct a right-angle in a semi-circle • Construct the perpendicular bisector of a line

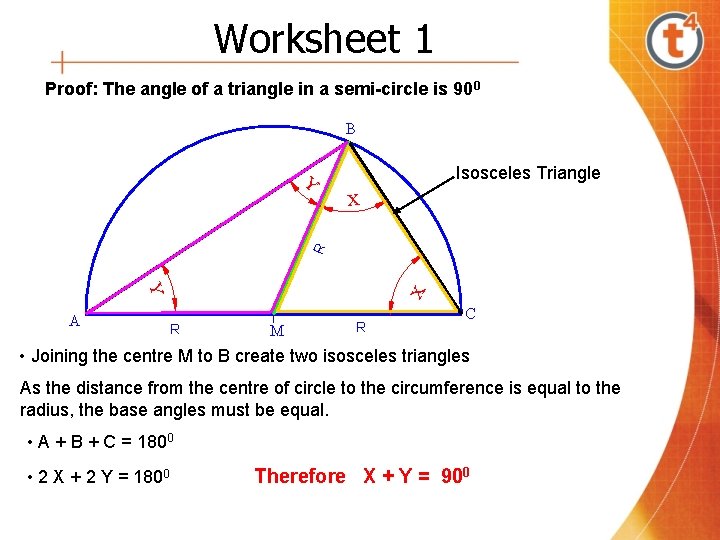
Worksheet 1 Proof: The angle of a triangle in a semi-circle is 900 B Isosceles Triangle x R Y x Y A R M R C • Joining the centre M to B create two isosceles triangles As the distance from the centre of circle to the circumference is equal to the radius, the base angles must be equal. • A + B + C = 1800 • 2 X + 2 Y = 1800 Therefore X + Y = 900

Worksheet 2

Worksheet 3

Worksheet 3 Having completed this worksheet, students should be able to • Apply knowledge of translations in solving solids in contact problems • Apply the principles of parallel lines in solving the problems • Locate the point of contact between a cone and a sphere

Worksheet 4

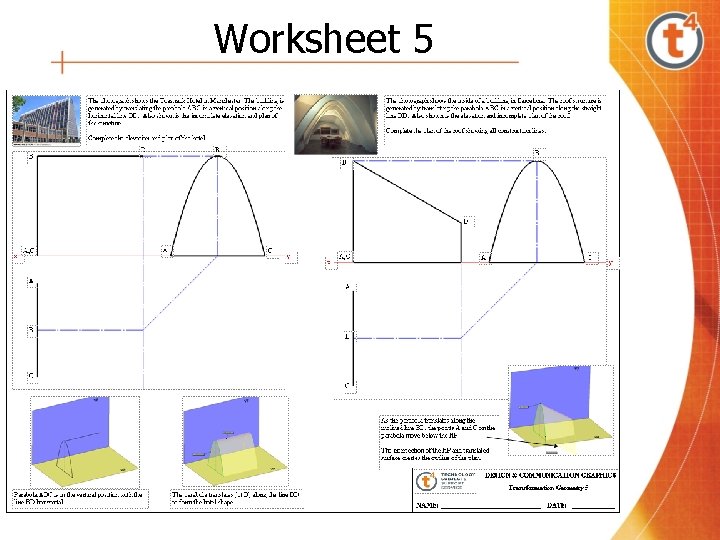
Worksheet 5

Worksheet 5 Having completed this worksheet, the students should be able to • Appreciate the existence of translations in the design and construction of buildings and structures • Identify how different shapes can be translated to create structures • Translate a parabola along a line in a vertical position • Determine the intersection of a parabola that is translated along an inclined line with the horizontal plane

Worksheet 6

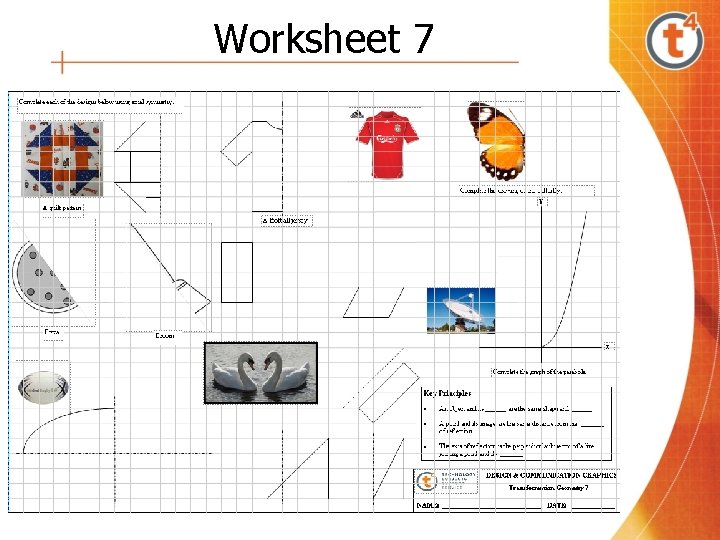
Worksheets 6, 7 & 8 Having completed this worksheet, the students should be able to • Identify and construct axes of symmetry in - geometric shapes - buildings - nature - everyday objects • Recognise that objects can have more than one axis of symmetry • Construct the images of plane figures under axial symmetry • Construct a composite of two reflections in two perpendicular lines • Use the method of axial symmetry to find the point of contact between a given ellipse and a tangent

Worksheet 7

Worksheet 8

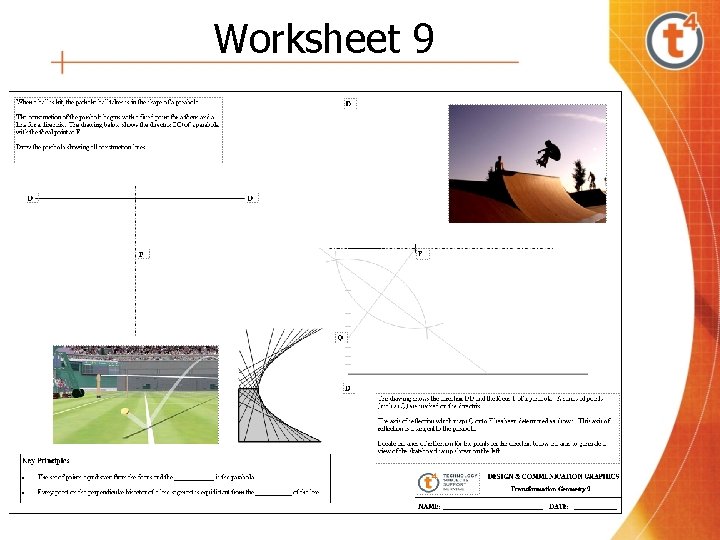
Worksheet 9

Worksheet 9 Having completed this worksheet, the students should be able to • Construct a parabola as a plane locus given the position of the directrix and the focus • Determine the axes of reflection which map a series of points on the directrix of a parabola onto the focus

Worksheet 10

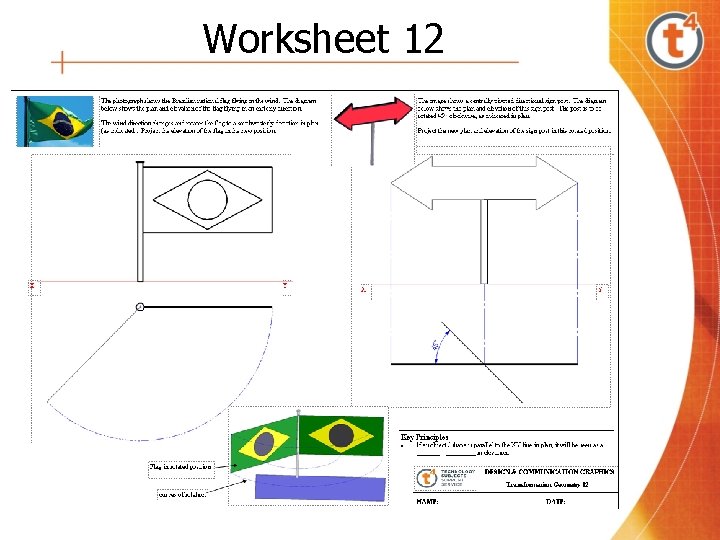
Worksheets 10, 11, 12 & 13 Having completed this worksheet, the students should be able to • Construct the rotation of a plane figure given the centre and angle of rotation • Appreciate that the rotation through 60 o of an equilateral triangle about one of its vertices will produce a hexagon • Recognise that all polygons can be constructed using a rotation of a triangle • Inscribe a polygon in a circle • Measure the angle of rotation having found the image

Worksheet 11

Worksheet 12

Worksheet 13

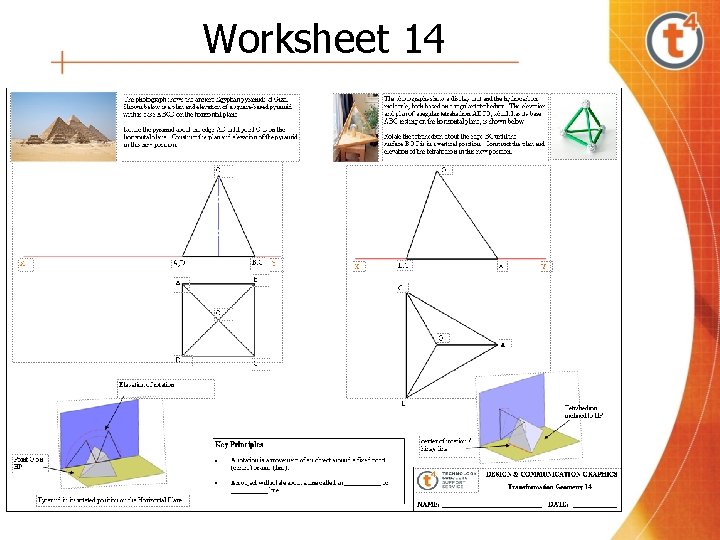
Worksheet 14

Worksheet 14 Having completed this worksheet, the students should be able to • Apply knowledge of rotations to solve the rotation of geometric solids. • Rotate a geometric solid into various positions with its surfaces on various planes.

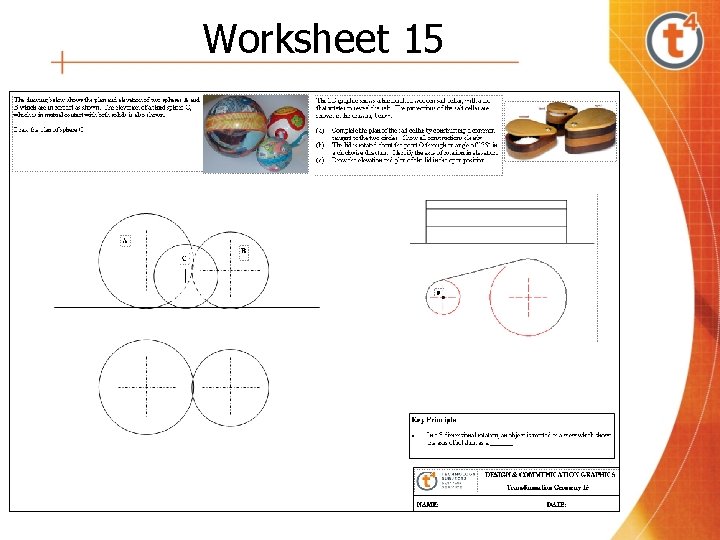
Worksheet 15

Worksheet 15 Having completed this worksheet, the students should be able to • Use the principle of loci as a problem solving tool • Construct loci in relation to circles and lines in one plane • Construct the plan of a sphere of given radius so that it is in mutual contact with two given spheres • Construct a common external tangent to two given circles of unequal radius • Construct the image of a plane figure under a rotation through a given angle

Worksheet 16

Worksheets 16 & 17 Having completed this worksheet, the students should be able to • Apply their knowledge of: 1. Translations 2. Central Symmetry 3. Axial Symmetry 4. Rotations in the solution of the given problems.

Worksheet 17