Design and Analysis of RF and Microwave Systems

Design and Analysis of RF and Microwave Systems IMPEDANCE TRANSFORMERS AND TAPERS Lecturers: March 2010 Lluís Pradell (pradell@tsc. upc. edu) Francesc Torres (xtorres@tsc. upc. edu)

Design and Analysis of RF and Microwave Systems The quarter-Wave Transformer* (i) A quarter-wave transformer can be used to match a real impedance ZL to Z 0 Zin Z 0 Z 1 If At a different frequency ZL The matching condition at fo is and the input reflection coefficient is The mismatch can be computed from: *Pozar 5. 5

Design and Analysis of RF and Microwave Systems The quarter-Wave Transformer (ii) If Return Loss is constrained to yield a maximum value , the frequency that reaches the bound can be computed from: Where for a TEM transmission line And the bound frequency is related to the design frequency as:

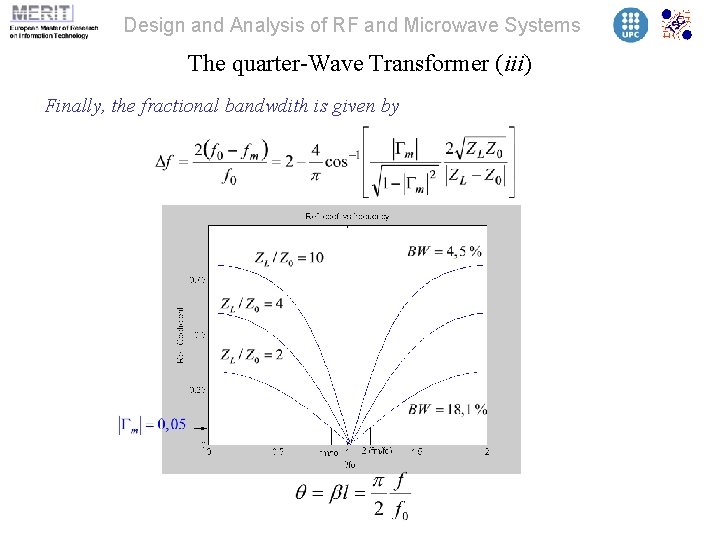
Design and Analysis of RF and Microwave Systems The quarter-Wave Transformer (iii) Finally, the fractional bandwdith is given by

Design and Analysis of RF and Microwave Systems Multisection transformer* (i) The theory of small reflections In the case of small reflections, the reflection coefficient can be approximated taking into account the partial (transient) reflection coefficients: That is, in the case of small reflections the permanent reflection is dominated by the two first transient terms: transmission line discontinuity and load *Pozar 5. 6

Design and Analysis of RF and Microwave Systems Multisection transformer (ii) The theory of small reflections can be extended to a multisection transformer It is assumed that the impedances ZN increase or decrease monotically The reflection coefficients can be grouped in pairs (ZN may not be symmetric)

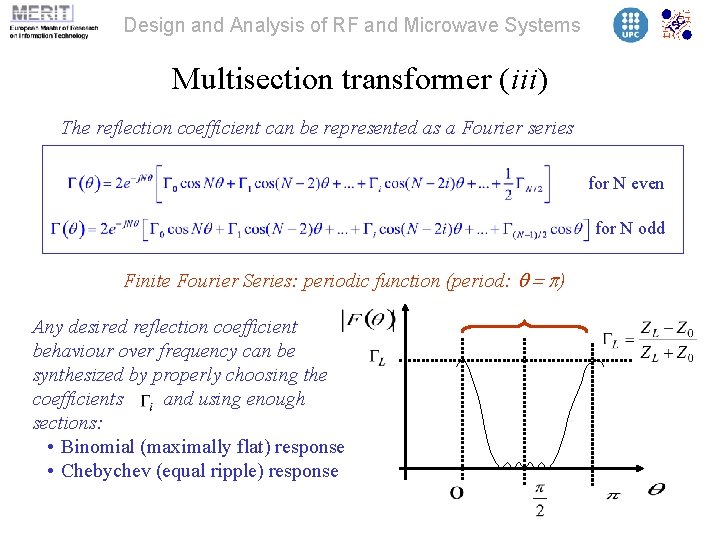
Design and Analysis of RF and Microwave Systems Multisection transformer (iii) The reflection coefficient can be represented as a Fourier series for N even for N odd Finite Fourier Series: periodic function (period: q = p) Any desired reflection coefficient behaviour over frequency can be synthesized by properly choosing the coefficients and using enough sections: • Binomial (maximally flat) response • Chebychev (equal ripple) response

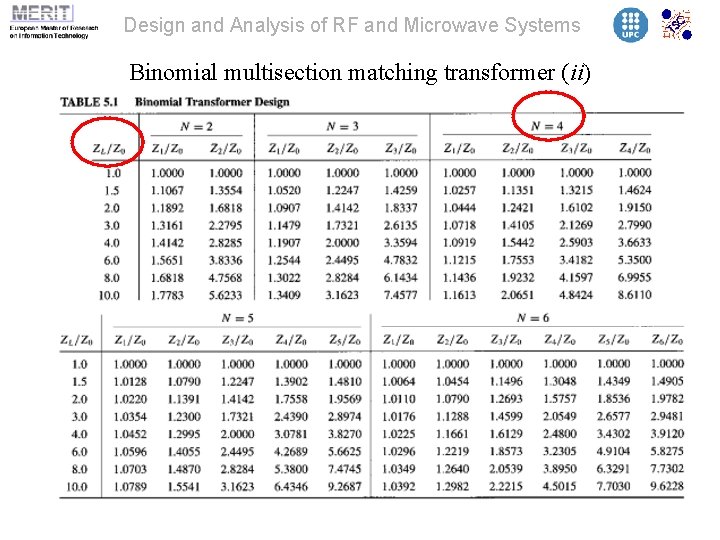
Design and Analysis of RF and Microwave Systems Binomial multisection matching transformer (i) Binomial function The constant A is computed from the transformer response at f=0: The transformer coefficients are computed from the response expansion: The transformer impedances Zn are then computed, starting from n=0, as:

Design and Analysis of RF and Microwave Systems Binomial multisection matching transformer (ii)

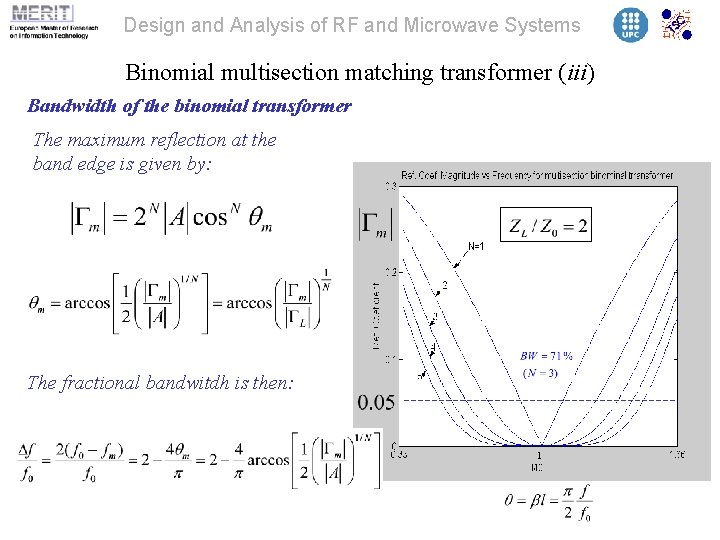
Design and Analysis of RF and Microwave Systems Binomial multisection matching transformer (iii) Bandwidth of the binomial transformer The maximum reflection at the band edge is given by: The fractional bandwitdh is then: 1

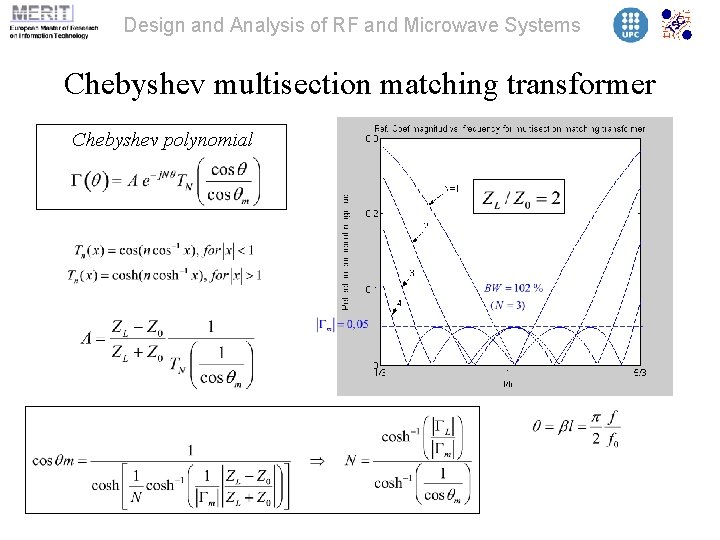
Design and Analysis of RF and Microwave Systems Chebyshev multisection matching transformer Chebyshev polynomial

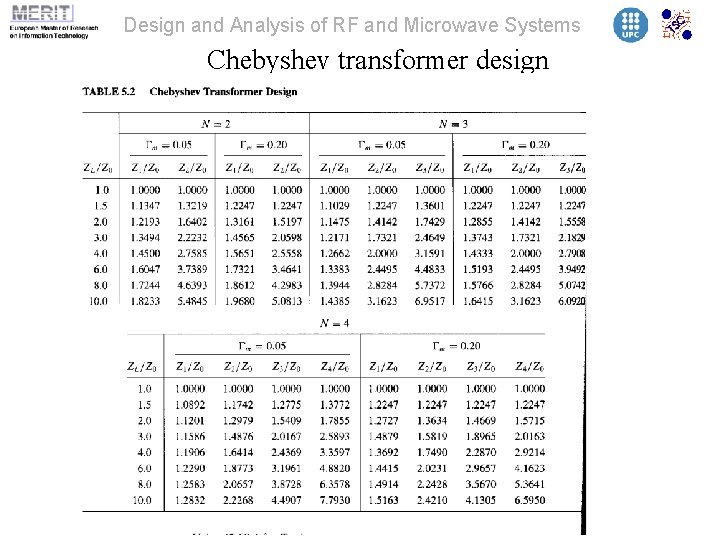
Design and Analysis of RF and Microwave Systems Chebyshev transformer design

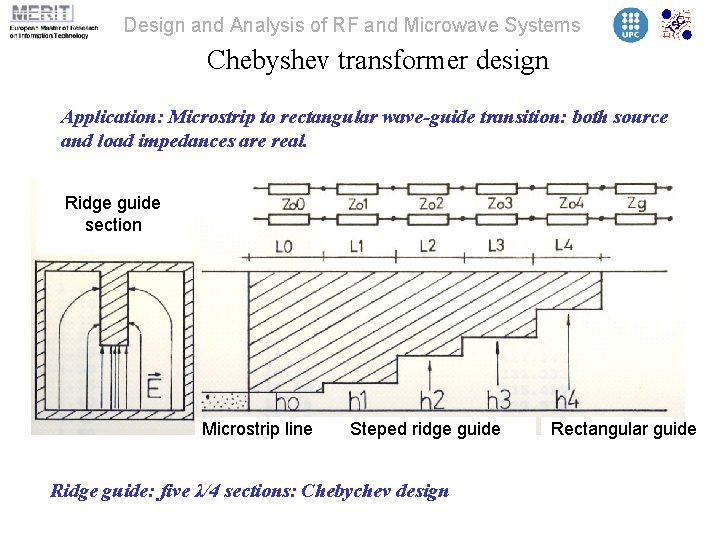
Design and Analysis of RF and Microwave Systems Chebyshev transformer design Application: Microstrip to rectangular wave-guide transition: both source and load impedances are real. Ridge guide section Microstrip line Steped ridge guide Ridge guide: five λ/4 sections: Chebychev design Rectangular guide

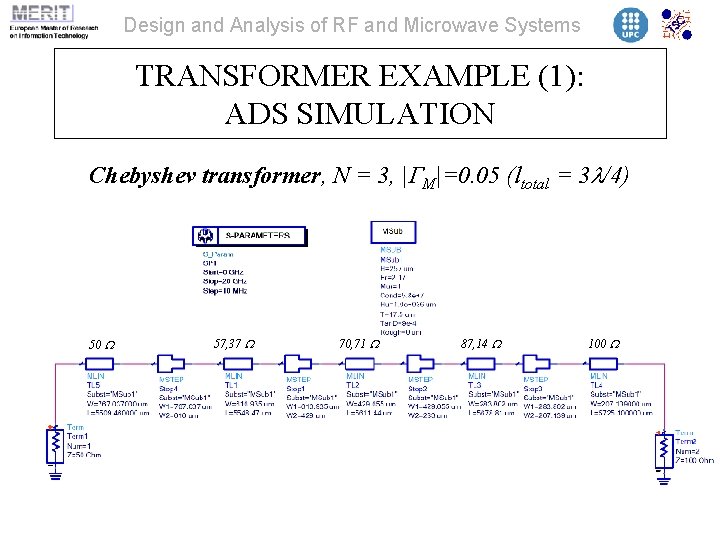
Design and Analysis of RF and Microwave Systems TRANSFORMER EXAMPLE (1): ADS SIMULATION Chebyshev transformer, N = 3, |GM|=0. 05 (ltotal = 3 l/4) 50 W 57, 37 W 70, 71 W 87, 14 W 100 W

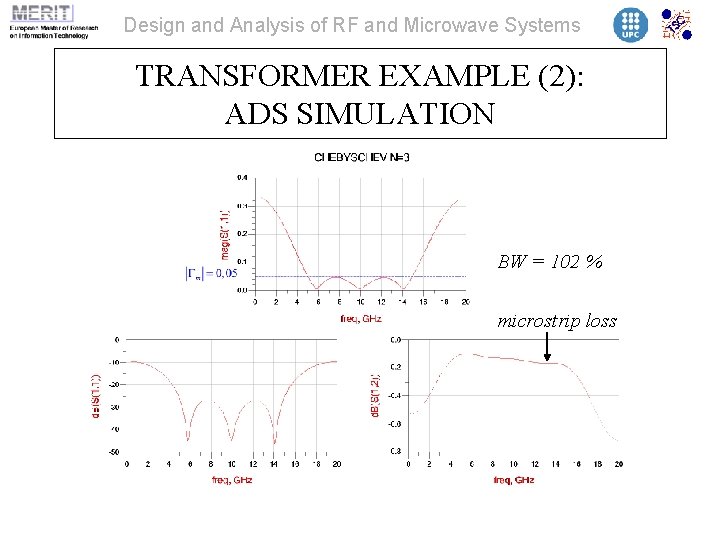
Design and Analysis of RF and Microwave Systems TRANSFORMER EXAMPLE (2): ADS SIMULATION BW = 102 % microstrip loss

Design and Analysis of RF and Microwave Systems Tapered lines (i) Taper: transmission line with smooth (progressive) varying impedance Z(z) The transient ΔΓ for a piece Δz of transmission line is given by: In the limit, when Dz 0: This expression can be developed taking into account the following property:

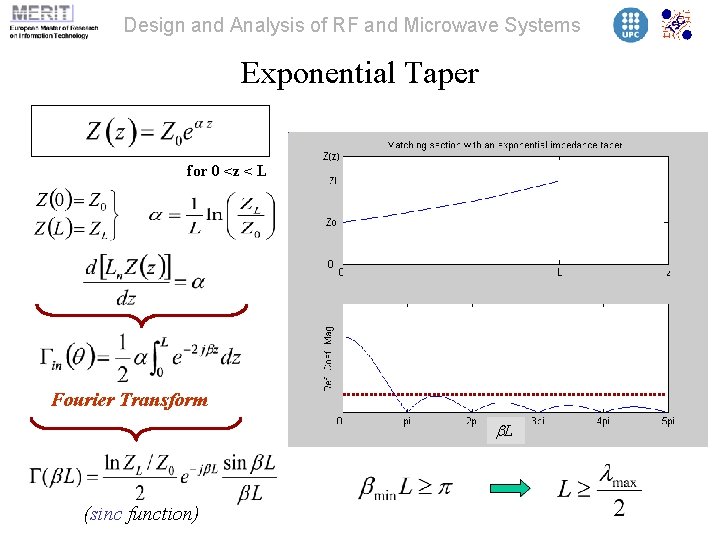
Design and Analysis of RF and Microwave Systems Tapered lines (ii) Taking into account theory of small reflections, the input reflection coefficient is the sum of all differential contributions, each one with its associated delay: Taper electrical length • Exponential taper • Triangular taper • Klopfenstein taper Fourier Transform

Design and Analysis of RF and Microwave Systems Exponential Taper for 0 <z < L Fourier Transform b. L (sinc function)

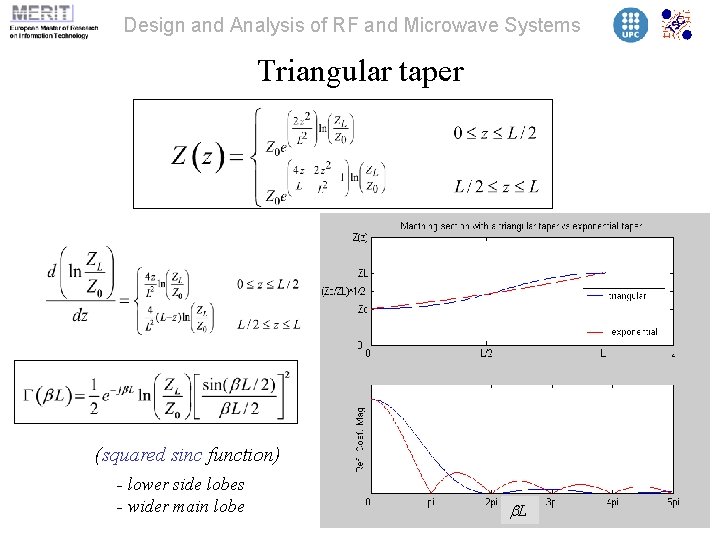
Design and Analysis of RF and Microwave Systems Triangular taper (squared sinc function) - lower side lobes - wider main lobe b. L

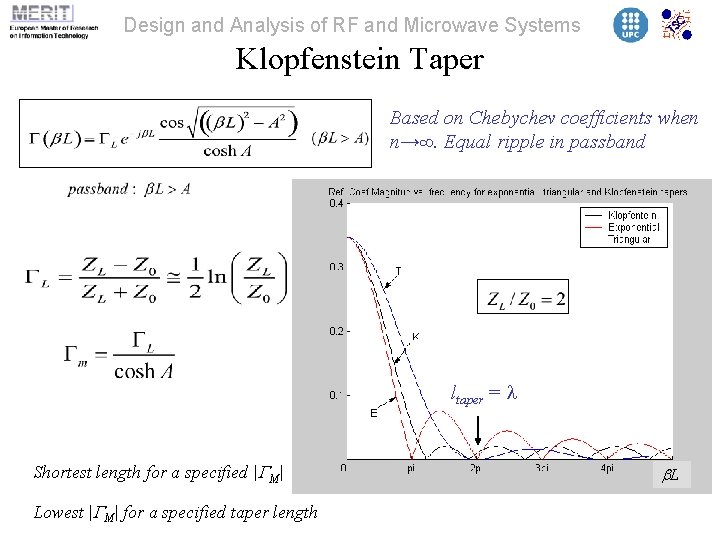
Design and Analysis of RF and Microwave Systems Klopfenstein Taper Based on Chebychev coefficients when n→∞. Equal ripple in passband ltaper = l Shortest length for a specified |GM| Lowest |GM| for a specified taper length b. L

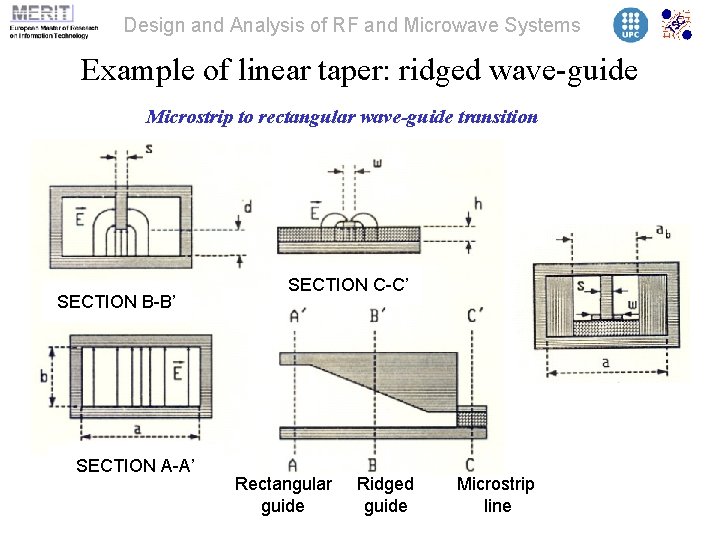
Design and Analysis of RF and Microwave Systems Example of linear taper: ridged wave-guide Microstrip to rectangular wave-guide transition SECTION B-B’ SECTION A-A’ SECTION C-C’ Rectangular guide Ridged guide Microstrip line

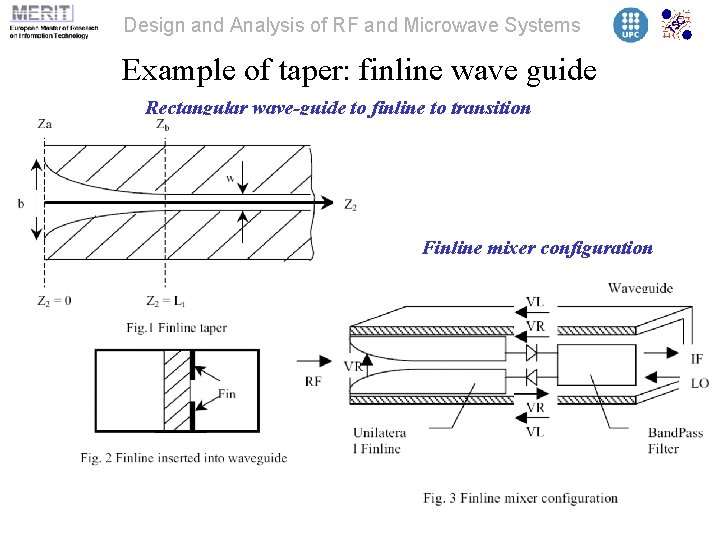
Design and Analysis of RF and Microwave Systems Example of taper: finline wave guide Rectangular wave-guide to finline to transition Finline mixer configuration

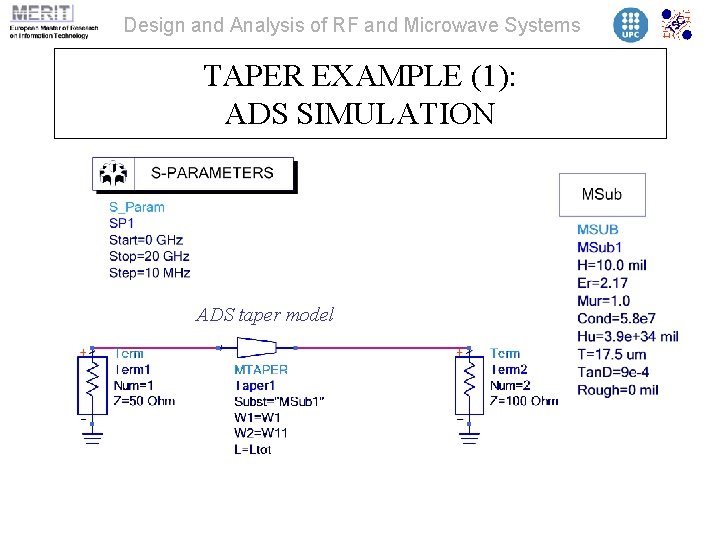
Design and Analysis of RF and Microwave Systems TAPER EXAMPLE (1): ADS SIMULATION ADS taper model

Design and Analysis of RF and Microwave Systems TAPER EXAMPLE (2): ADS SIMULATION Aproximation to exponential taper using ADS : 10 sections of l/10 50 W 57, 44 W 53, 59 W 100 W 93, 30 W 61, 56 W 87, 05 W 65, 97 W 81, 22 W 70, 71 W 75, 79 W

Design and Analysis of RF and Microwave Systems TAPER EXAMPLE (3): ADS SIMULATION Aproximation to exponential taper using ADS : 10 sections of l/10 50 W 53, 59 W 57, 44 W 61, 56 W 70, 71 W 75, 79 W 81, 22 W 87, 05 W 100 W 65, 97 W 93, 30 W

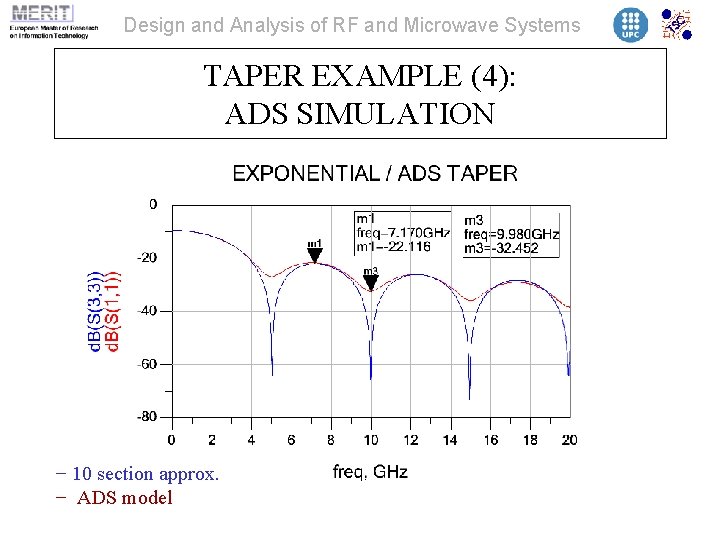
Design and Analysis of RF and Microwave Systems TAPER EXAMPLE (4): ADS SIMULATION − 10 section approx. − ADS model

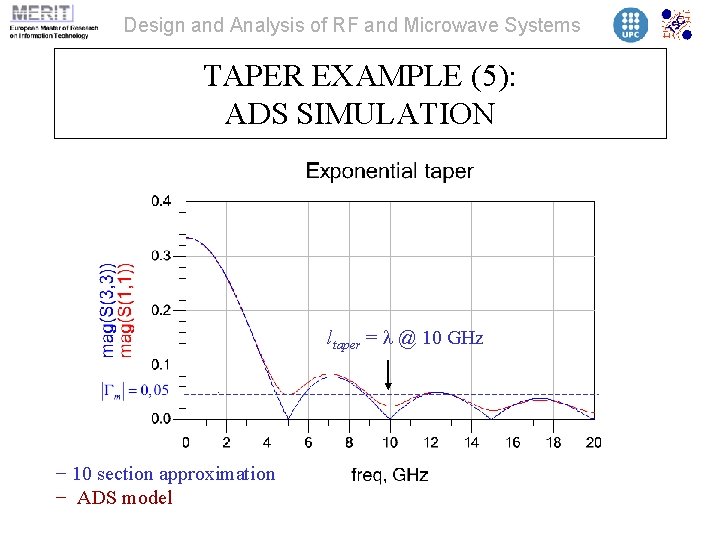
Design and Analysis of RF and Microwave Systems TAPER EXAMPLE (5): ADS SIMULATION ltaper = l @ 10 GHz − 10 section approximation − ADS model

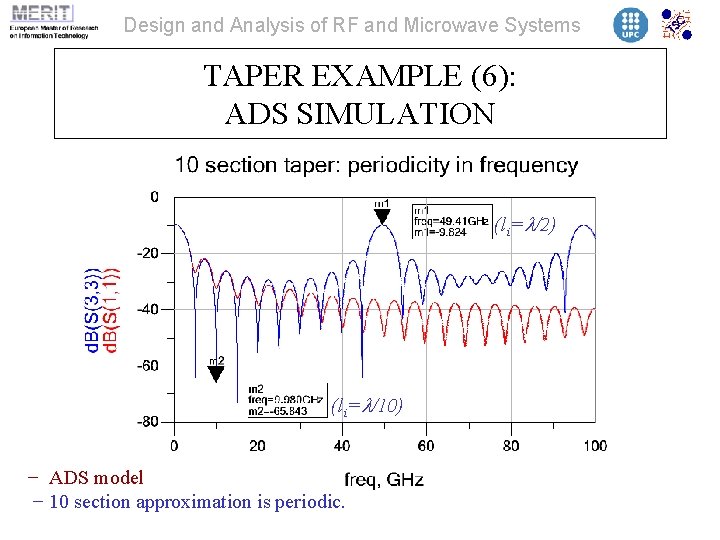
Design and Analysis of RF and Microwave Systems TAPER EXAMPLE (6): ADS SIMULATION (li=l/2) (li=l/10) − ADS model − 10 section approximation is periodic.

Design and Analysis of RF and Microwave Systems MATCHING NETWORKS LEVY DESIGN Lecturers: Lluís Pradell (pradell@tsc. upc. edu) Francesc Torres (xtorres@tsc. upc. edu)

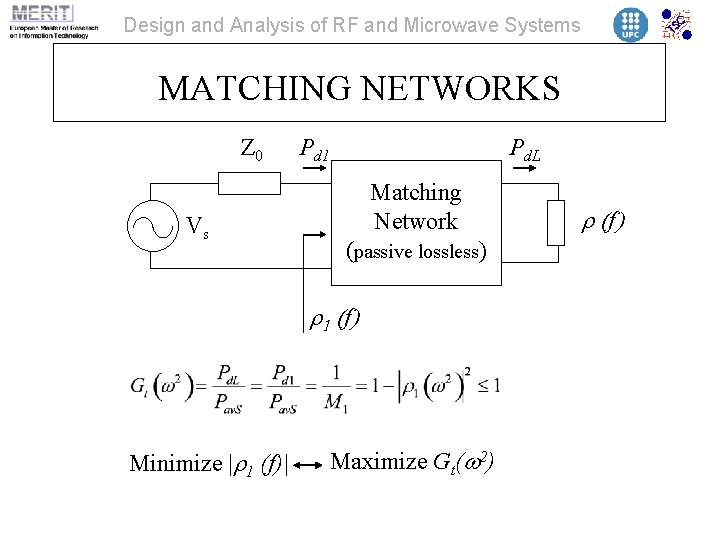
Design and Analysis of RF and Microwave Systems MATCHING NETWORKS Z 0 Vs Pd 1 Pd. L Matching Network (passive lossless) r 1 (f ) Minimize |r 1 (f)| Maximize Gt(w 2) r (f)

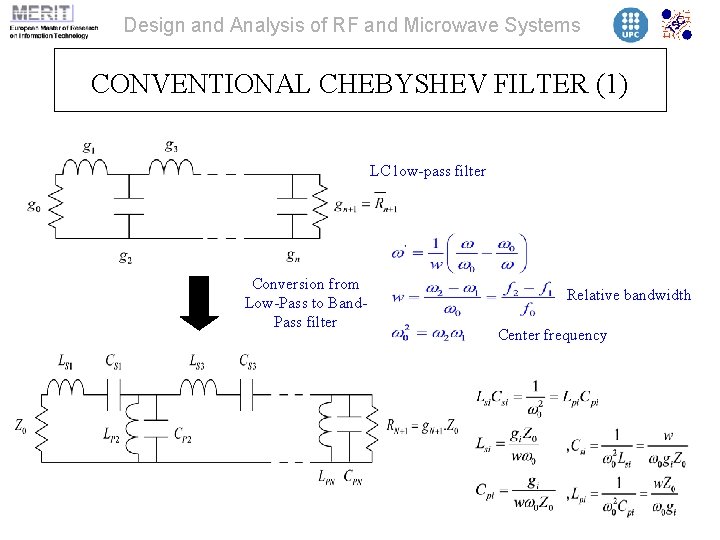
Design and Analysis of RF and Microwave Systems CONVENTIONAL CHEBYSHEV FILTER (1) LC low-pass filter Conversion from Low-Pass to Band. Pass filter Relative bandwidth Center frequency

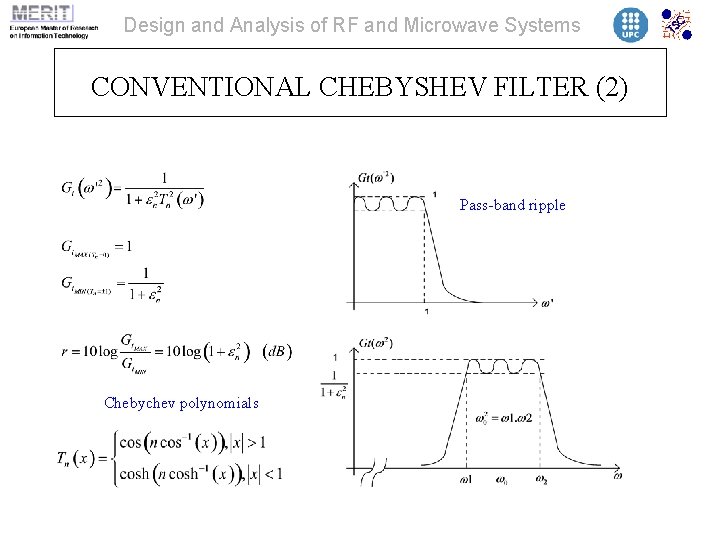
Design and Analysis of RF and Microwave Systems CONVENTIONAL CHEBYSHEV FILTER (2) Pass-band ripple Chebychev polynomials

Design and Analysis of RF and Microwave Systems CONVENTIONAL CHEBYSHEV FILTER (3) Fix pass-band ripple and filter order “n” g 0, g 1, . . , gn+1 are the low-pass LC filter coefficients:

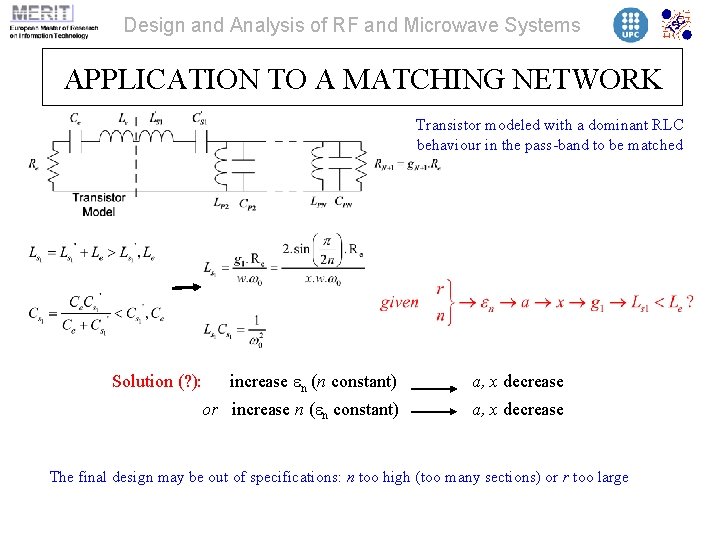
Design and Analysis of RF and Microwave Systems APPLICATION TO A MATCHING NETWORK Transistor modeled with a dominant RLC behaviour in the pass-band to be matched increase en (n constant) a, x decrease or increase n (en constant) a, x decrease Solution (? ): The final design may be out of specifications: n too high (too many sections) or r too large

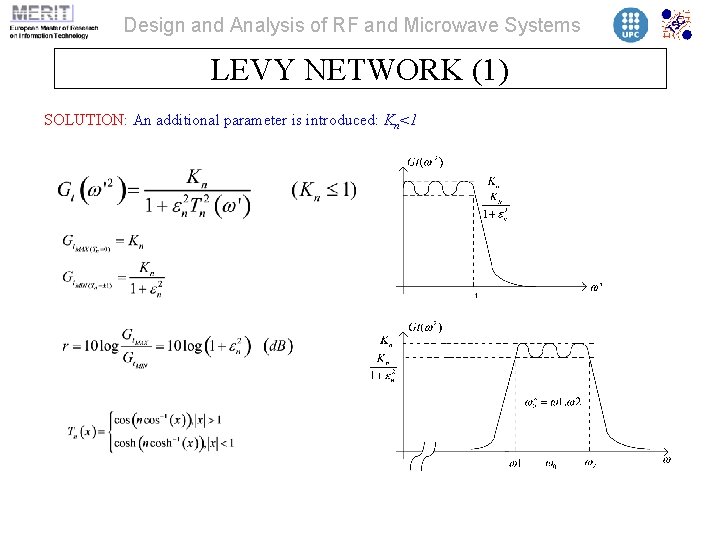
Design and Analysis of RF and Microwave Systems LEVY NETWORK (1) SOLUTION: An additional parameter is introduced: Kn<1

Design and Analysis of RF and Microwave Systems LEVY NETWORK (2) SOLUTION: Additional design equations Example: n = 2

Design and Analysis of RF and Microwave Systems LEVY NETWORK (3) Design procedure a) Choose Cs 1 or Ls 1 taking into account the load to be matched b) Choose network order (n) and compute g 1 c) Compute x-y from the parameter g 1

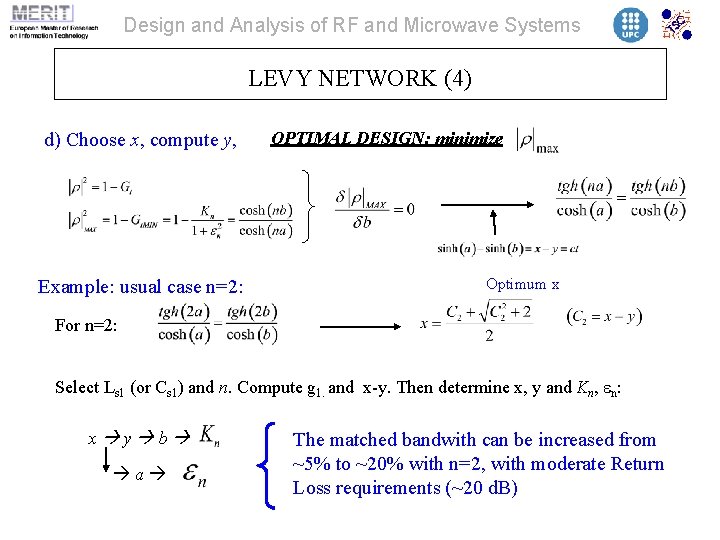
Design and Analysis of RF and Microwave Systems LEVY NETWORK (4) d) Choose x, compute y, Example: usual case n=2: OPTIMAL DESIGN: minimize Optimum x For n=2: Select Ls 1 (or Cs 1) and n. Compute g 1. and x-y. Then determine x, y and Kn, en: x y b a The matched bandwith can be increased from ~5% to ~20% with n=2, with moderate Return Loss requirements (~20 d. B)

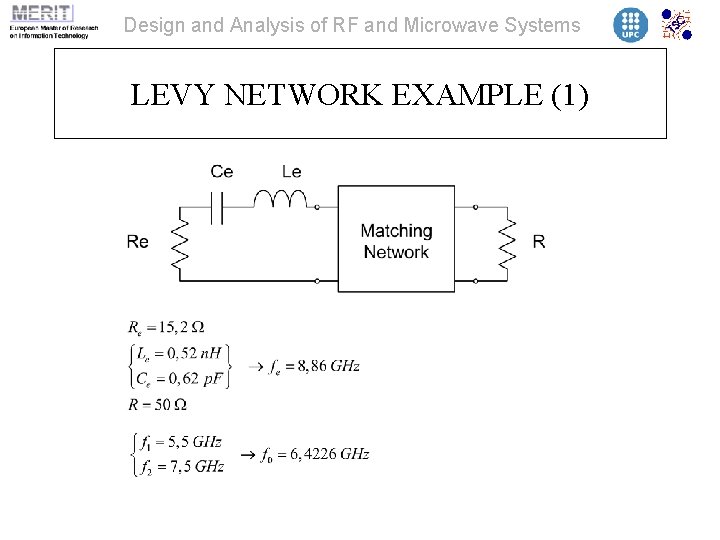
Design and Analysis of RF and Microwave Systems LEVY NETWORK EXAMPLE (1)

Design and Analysis of RF and Microwave Systems LEVY NETWORK EXAMPLE (2)

Design and Analysis of RF and Microwave Systems LEVY NETWORK EXAMPLE (3): ADS SIMULATION A transformer is necessary since g 3≠ 1 (R 3≠ 50 Ω). This transformed must be eliminated from the design

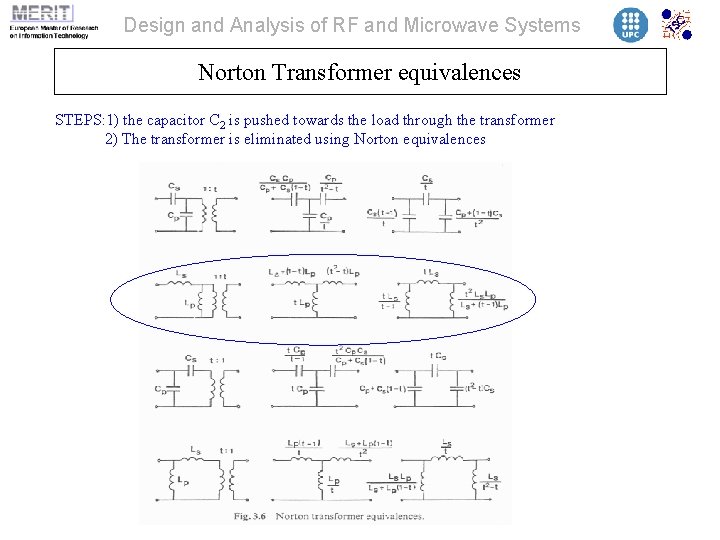
Design and Analysis of RF and Microwave Systems Norton Transformer equivalences STEPS: 1) the capacitor C 2 is pushed towards the load through the transformer 2) The transformer is eliminated using Norton equivalences

Design and Analysis of RF and Microwave Systems LEVY NETWORK EXAMPLE (4): ADS SIMULATION

Design and Analysis of RF and Microwave Systems SMALL SERIES INDUCTANCES AND PARALLEL CAPACITANCES IMPLEMENTED USING SHORT TRANSMISSION LINES L, C elements are then synthesized by means of short transmission lines:

Design and Analysis of RF and Microwave Systems SMALL SERIES INDUCTANCES AND PARALLEL CAPACITANCES IMPLEMENTED USING SHORT TRANSMISSION LINES: EXAMPLE

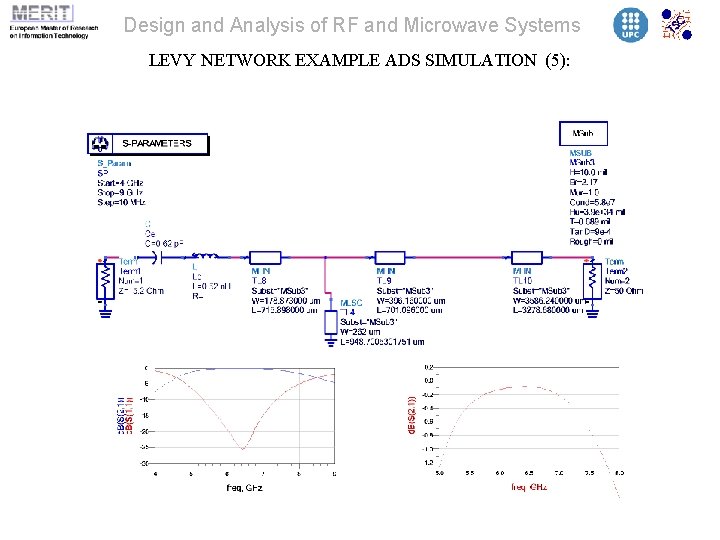
Design and Analysis of RF and Microwave Systems LEVY NETWORK EXAMPLE ADS SIMULATION (5):

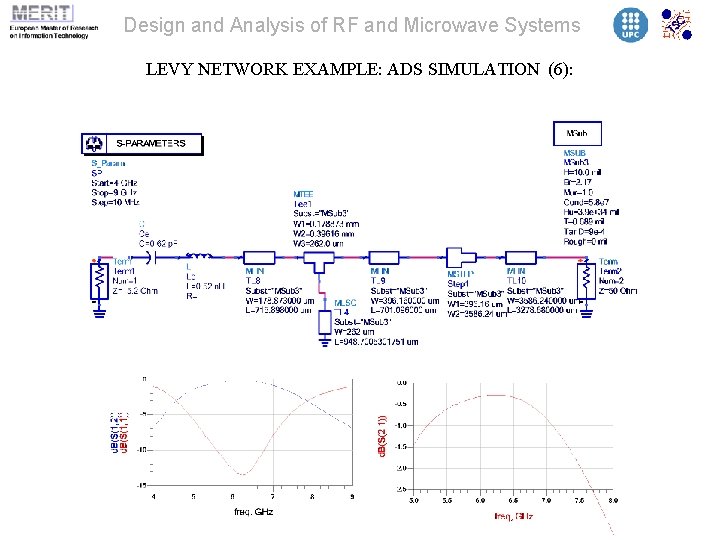
Design and Analysis of RF and Microwave Systems LEVY NETWORK EXAMPLE: ADS SIMULATION (6):

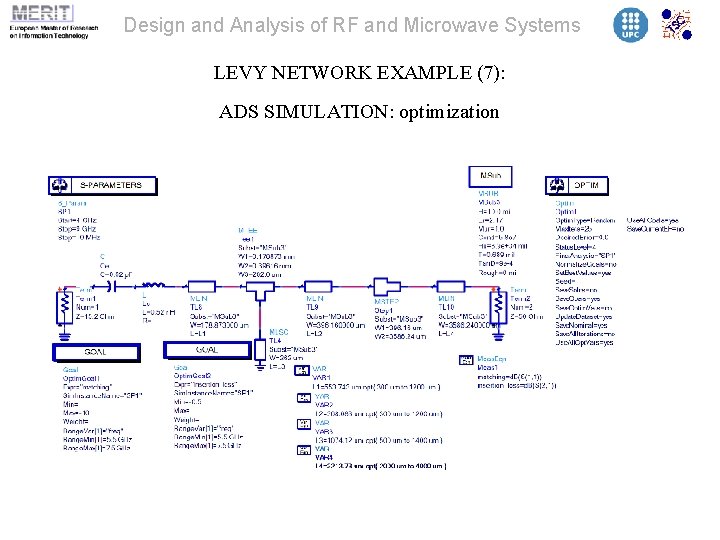
Design and Analysis of RF and Microwave Systems LEVY NETWORK EXAMPLE (7): ADS SIMULATION: optimization

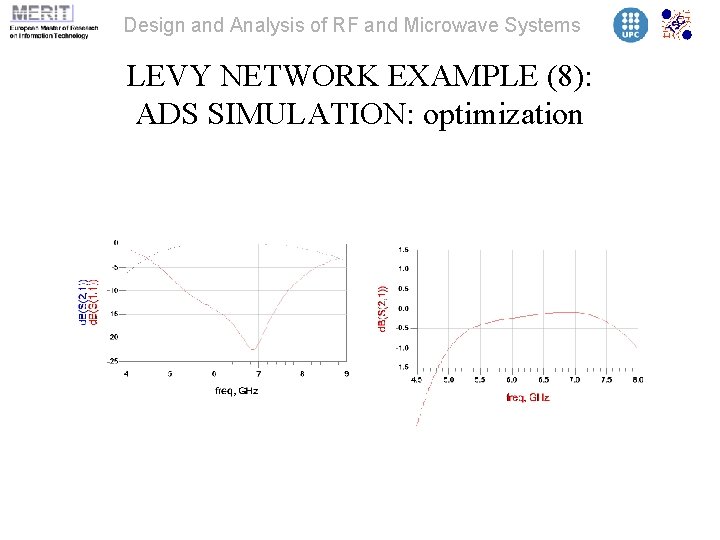
Design and Analysis of RF and Microwave Systems LEVY NETWORK EXAMPLE (8): ADS SIMULATION: optimization

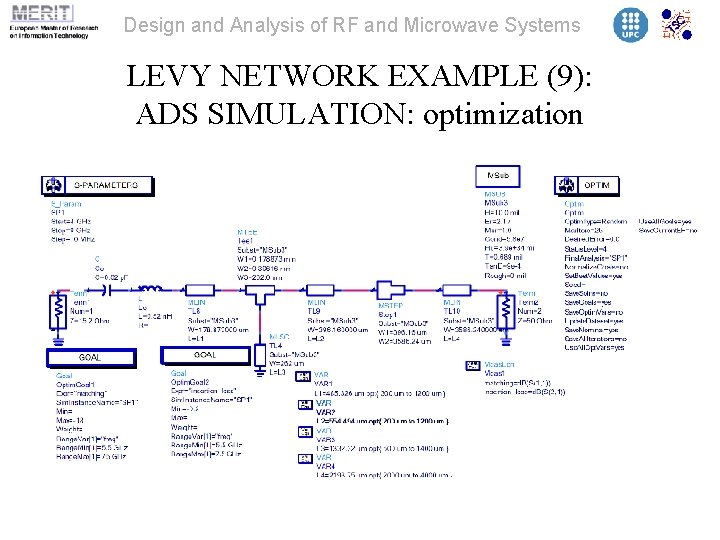
Design and Analysis of RF and Microwave Systems LEVY NETWORK EXAMPLE (9): ADS SIMULATION: optimization

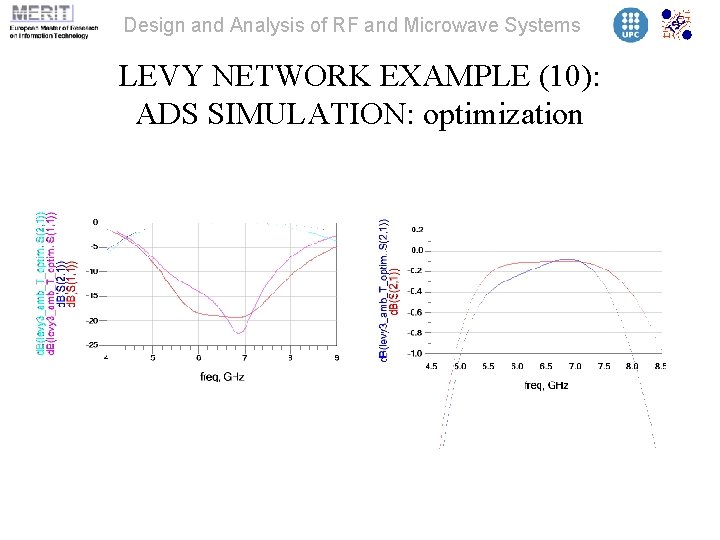
Design and Analysis of RF and Microwave Systems LEVY NETWORK EXAMPLE (10): ADS SIMULATION: optimization