Design and Analysis of MultiFactored Experiments Fractional Factorial

Design and Analysis of Multi-Factored Experiments Fractional Factorial Designs L. M. Lye DOE Course 1

Design of Engineering Experiments – The 2 k-p Fractional Factorial Design • Motivation for fractional factorials is obvious; as the number of factors becomes large enough to be “interesting”, the size of the designs grows very quickly • Emphasis is on factor screening; efficiently identify the factors with large effects • There may be many variables (often because we don’t know much about the system) • Almost always run as unreplicated factorials, but often with center points L. M. Lye DOE Course 2

Why do Fractional Factorial Designs Work? • The sparsity of effects principle – There may be lots of factors, but few are important – System is dominated by main effects, low-order interactions • The projection property – Every fractional factorial contains full factorials in fewer factors • Sequential experimentation – Can add runs to a fractional factorial to resolve difficulties (or ambiguities) in interpretation L. M. Lye DOE Course 3

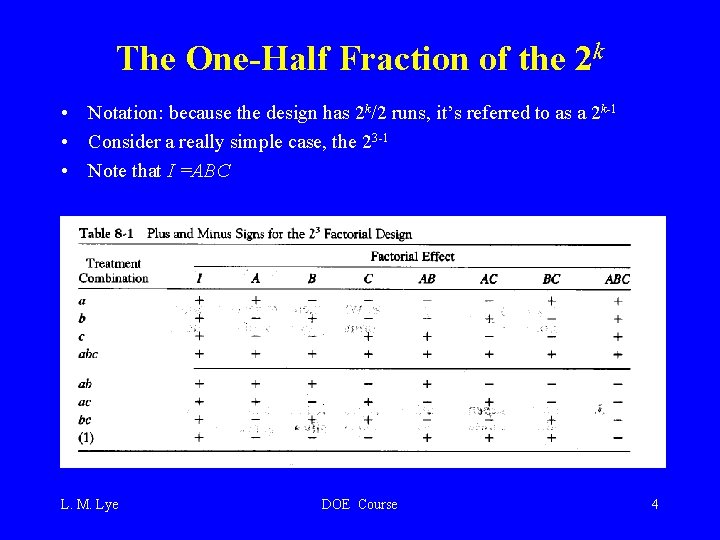
The One-Half Fraction of the 2 k • Notation: because the design has 2 k/2 runs, it’s referred to as a 2 k-1 • Consider a really simple case, the 23 -1 • Note that I =ABC L. M. Lye DOE Course 4

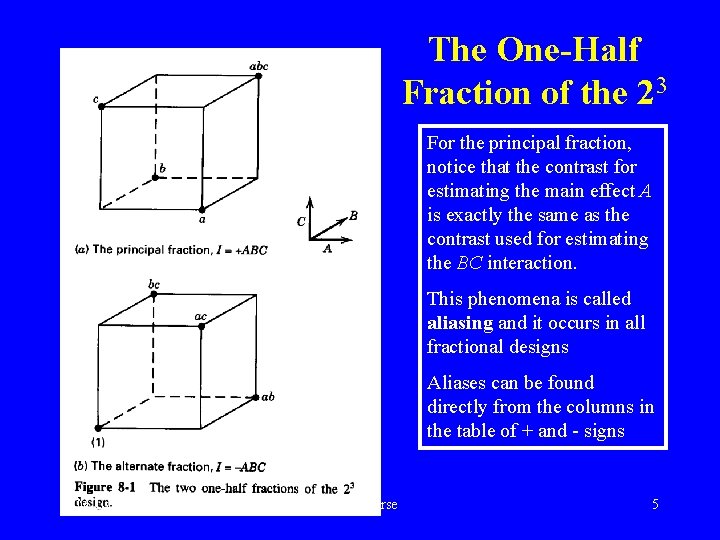
The One-Half Fraction of the 23 For the principal fraction, notice that the contrast for estimating the main effect A is exactly the same as the contrast used for estimating the BC interaction. This phenomena is called aliasing and it occurs in all fractional designs Aliases can be found directly from the columns in the table of + and - signs L. M. Lye DOE Course 5

The Alternate Fraction of the 23 -1 • I = -ABC is the defining relation • Implies slightly different aliases: A = -BC, B= -AC, and C = -AB • Both designs belong to the same family, defined by • Suppose that after running the principal fraction, the alternate fraction was also run • The two groups of runs can be combined to form a full factorial – an example of sequential experimentation L. M. Lye DOE Course 6

Example: Run 4 of the 8 t. c. ’s in 23: a, b, c, abc It is clear that from the(se) 4 t. c. ’s, we cannot estimate the 7 effects (A, B, AB, C, AC, BC, ABC) present in any 23 design, since each estimate uses (all) 8 t. c’s. What can be estimated from these 4 t. c. ’s? L. M. Lye DOE Course 7

4 A = -1 + a - b + ab - c + ac - bc + abc 4 BC = 1 + a - b - ab -c - ac + bc + abc Consider (4 A + 4 BC)= 2(a - b - c + abc) or 2(A + BC)= a - b - c + abc Overall: 2(A + BC)= a - b - c + abc 2(B + AC)= -a + b - c + abc 2(C + AB)= -a - b + c + abc In each case, the 4 t. c. ’s NOT run cancel out. L. M. Lye DOE Course 8

Had we run the other 4 t. c. ’s: 1, ab, ac, bc, We would be able to estimate A - BC B - AC C - AB (generally no better or worse than with + signs) NOTE: If you “know” (i. e. , are willing to assume) that all interactions = 0, then you can say either (1) you get 3 factors for “the price” of 2. (2) you get 3 factors at “ 1/2 price. ” L. M. Lye DOE Course 9

Suppose we run those 4: 1, ab, c, abc; We would then estimate A+B two main effects C + ABC together usually less desirable AC + BC In each case, we “Lose” 1 effect completely, and get the other 6 in 3 pairs of two effects. Members of the pair are CONFOUNDED Members of the pair are ALIASED L. M. Lye DOE Course 10

With 4 t. c. ’s, one should expect to get only 3 “estimates” (or “alias pairs”) - NOT unrelated to “degrees of freedom being one fewer than # of data points” or “with c columns, we get (c - 1) df. ” In any event, clearly, there are BETTER and WORSE sets of 4 t. c. ’s out of a 23. (Better & worse 23 -1 designs) L. M. Lye DOE Course 11

Prospect in fractional factorial designs is attractive if in some or all alias pairs one of the effects is KNOWN. This usually means “thought to be zero” L. M. Lye DOE Course 12

Consider a 24 -1 with t. c. ’s 1, ab, ac, bc, ad, bd, cd, abcd Can estimate: A+BCD B+ACD C+ABD AB+CD AC+BD BC+AD D+ABC Note: L. M. Lye - 8 t. c. ’s -Lose 1 effect -Estimate other 14 in 7 alias pairs of 2 DOE Course 13

“Clean” estimates of the remaining member of the pair can then be made. For those who believe, by conviction or via selected empirical evidence, that the world is relatively simple, 3 and higher order interactions (such as ABC, ABCD, etc. ) may be announced as zero in advance of the inquiry. In this case, in the 24 -1 above, all main effects are CLEAN. Without any such belief, fractional factorials are of uncertain value. After all, you could get A + BCD = 0, yet A could be large +, BCD large -; or the reverse; or both zero. L. M. Lye DOE Course 14

Despite these reservations fractional factorials are almost inevitable in a many factor situation. It is generally better to study 5 factors with a quarter replicate (25 -2 = 8) than 3 factors completely (23 = 8). Whatever else the real world is, it’s Multifactored. The best way to learn “how” is to work (and discuss) some examples: L. M. Lye DOE Course 15

Design and Analysis of Multi-Factored Experiments Aliasing Structure L. M. Lye DOE Course 16

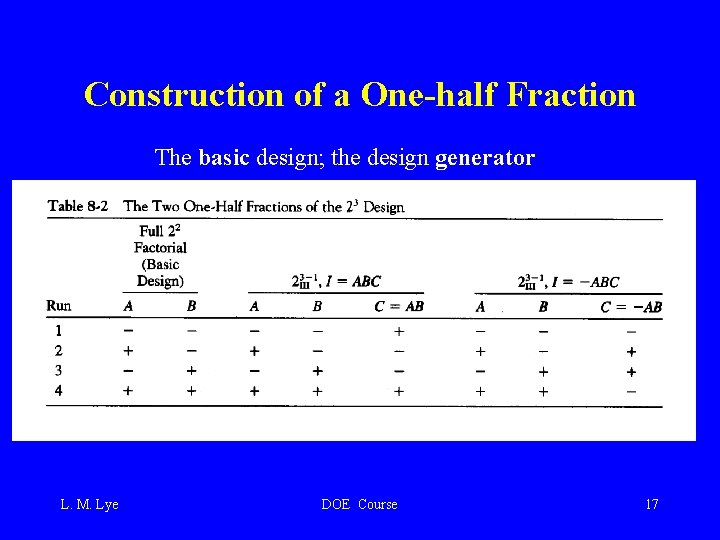
Construction of a One-half Fraction The basic design; the design generator L. M. Lye DOE Course 17

Example: 25 -1 : A, B, C, D, E Step 1: In a 2 k-p, we “lose” 2 p-1. Here we lose 1. Choose the effect to lose. Write it as a “Defining relation” or “Defining contrast. ” I = ABDE Step 2: Find the resulting alias pairs: *A=BDE AB=DE ABC=CDE - lose 1 B=ADE AC=4 BCD=ACE - other 30 in 15 C=ABCDE AD=BE BCE=ACD alias pairs of 2 D=ABE AE=BD - run 16 t. c. ’s E=ABD BC=4 15 estimates CD=4 CE=4 *Ax. ABDE=BDE L. M. Lye DOE Course 18

See if they are (collectively) acceptable. Another option (among many others): I = ABCDE A=4 B=4 C=4 D=4 E=4 L. M. Lye AB=3 AC=3 AD=3 AE=3 BC=3 BD=3 BE=3 CD=3 CE=3 DOE Course 19

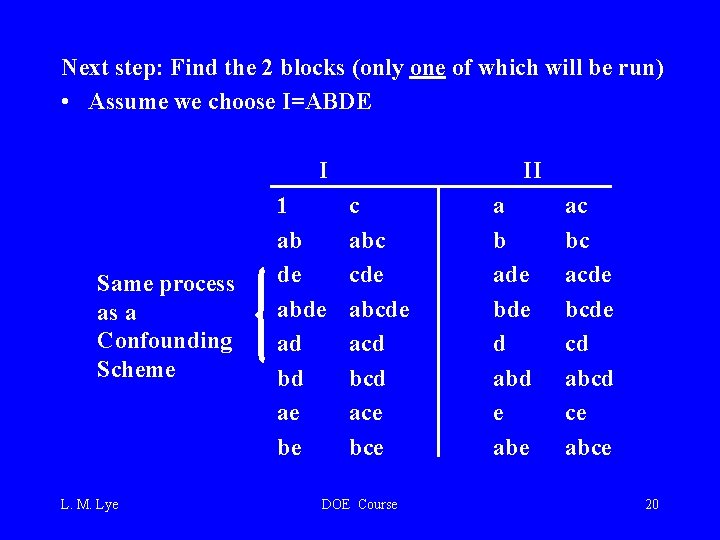
Next step: Find the 2 blocks (only one of which will be run) • Assume we choose I=ABDE I Same process as a Confounding Scheme L. M. Lye 1 ab de abde ad bd ae be II c abc cde abcde acd bcd ace bce DOE Course a b ade bde d abd e abe ac bc acde bcde cd abcd ce abce 20

Next: Pick which block to run. (say, block II) Next: Go out and collect the data. Next: Analyze it. a. ) find a proper Yates’ order. i. ) pick a letter and for a moment call it “DEAD. ” (assume we pick “d”) ii. ) use the remaining (“live”) letters to form the STANDARD Yates’ order: (see right column) Now append the dead letter as needed to form the block chosen to be run: L. M. Lye DOE Course 1 a b ab c ac bc abc e ae be abe ce ace bce abce 21

There’s only one way to do it, i. e. either adding “d” or not adding “d”; one way will work, one won’t. L. M. Lye DOE Course 22

Example 2: In a 25 , there are 31 effects; with 8 t. c. , there are 7 df & 7 estimates available L. M. Lye 25 -2 A, B, C, D, E Must “lose” 3; other 28 in 7 alias groups of 4 DOE Course 23

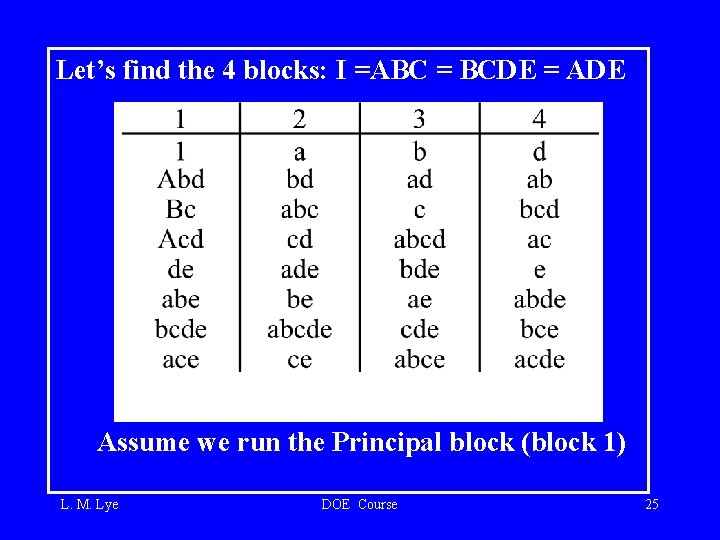
Choose the 3: Like in confounding schemes, 3 rd must be product of first 2: I = ABC = BCDE = ADE A = BC B = AC C = AB Find alias D = 4 groups: E = 4 BD = 3 BE = 3 = 5 = DE = 3 = 4 = 3 = AE = 3 = AD = CE = 3 = CD = 3 Assume we use this design. L. M. Lye DOE Course 24

Let’s find the 4 blocks: I =ABC = BCDE = ADE Assume we run the Principal block (block 1) L. M. Lye DOE Course 25

Run the 8 t. c. ’s and analyze: Since it’s a 25 -2, we designate 2 letters as “DEAD” (say b, d), write a standard Yates’ order in the other (3) (live) letters, and append the dead letters to form the t. c. ’s being run: I = ABC = BCDE = ADE t. c. 1 a (bd) c (b) ac (d) e (d) ae (b) ce ( bd) ace L. M. Lye yield (1) (2) . . . . DOE Course (3) Estimate A -2+5 -2 C -2+3 -4 AC - B +4 -3 E -4+3 -2 AE -3+4 - D CE -3+2 -3 ACE -2+3 -2 26

Good to know rule: t. c. with even # letters in common with even-lettered effect is a + for that effect; t. c. with odd # letters in common with odd-lettered effect is a + for that effect; otherwise a - (minus) # letters in effect Even Odd # letters t. c. has in Even Common with Effect Odd abd in ABCDE: 3 in common with 5 ODD with ODD + abce in ABCDFG: 3 in common with 6 ODD with EVEN L. M. Lye DOE Course 27

Examples L. M. Lye DOE Course 28

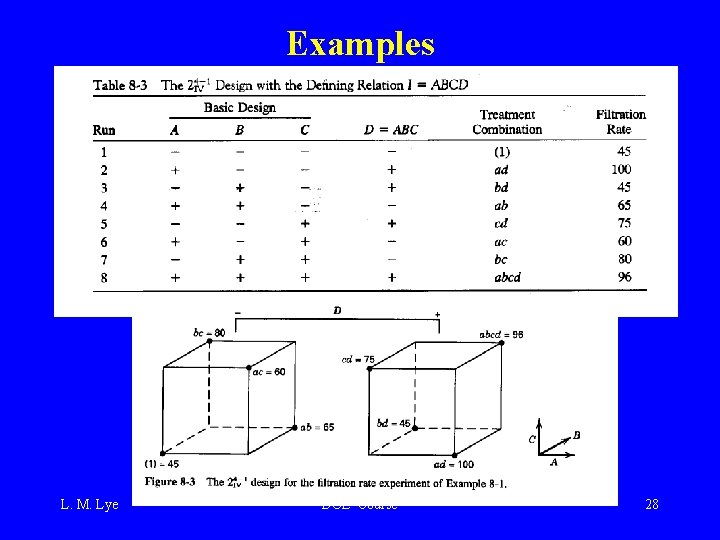
Example Interpretation of results often relies on making some assumptions Ockham’s razor Confirmation experiments can be important See the projection of this design into 3 factors L. M. Lye DOE Course 29

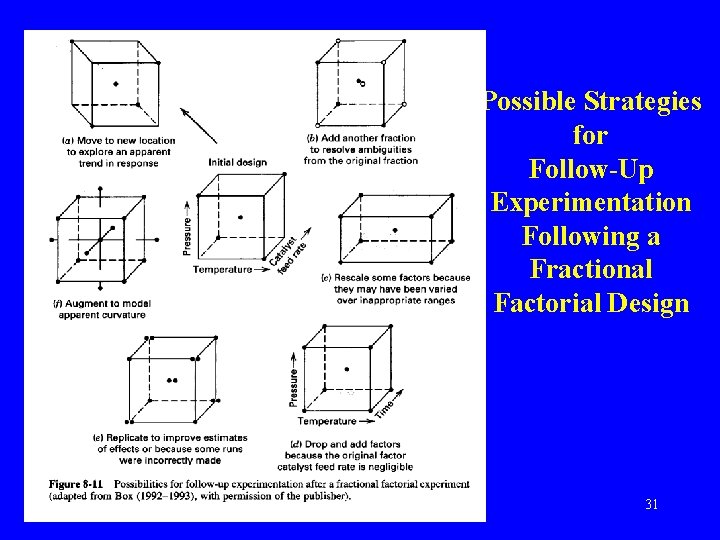
Projection of Fractional Factorials Every fractional factorial contains full factorials in fewer factors The “flashlight” analogy A one-half fraction will project into a full factorial in any k – 1 of the original factors L. M. Lye DOE Course 30

Possible Strategies for Follow-Up Experimentation Following a Fractional Factorial Design L. M. Lye DOE Course 31

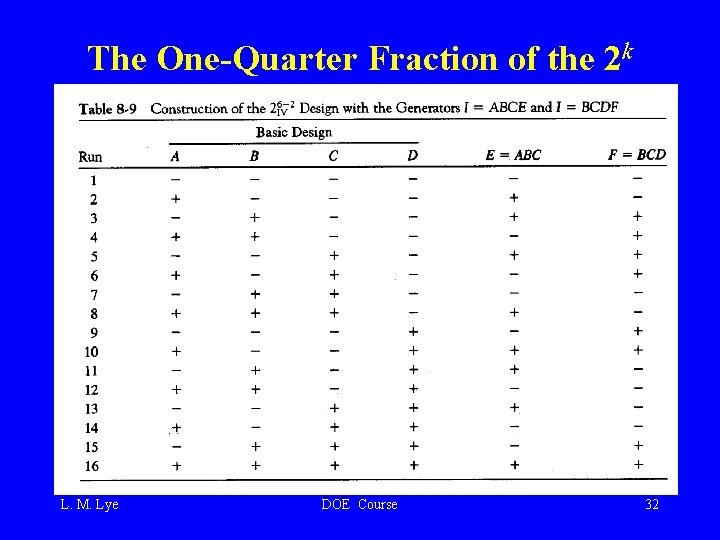
The One-Quarter Fraction of the 2 k L. M. Lye DOE Course 32

The One-Quarter Fraction of the 26 -2 Complete defining relation: I = ABCE = BCDF = ADEF L. M. Lye DOE Course 33

Analysis of Fractional Factorials • Easily done by computer • Same method as full factorial except that effects are aliased • All other steps same as full factorial e. g. ANOVA, normal plots, etc. • Important not to use highly fractionated designs - waste of resources because “clean” estimates cannot be made. L. M. Lye DOE Course 34