Design and Analysis of Algorithms By Mrs Urmila

Design and Analysis of Algorithms By Mrs. Urmila Kalshetti

Introduction Analysis of Algorithms

What is Algorithm? �“Algorithm is more than the branch of computer science. It is the core of computer science, and, in all fairness, can be said to be relevant it most of science, business and technology” �An algorithm is a sequence of unambiguous instruction for solving a problem, for obtaining a required output for any legitimate input in a finite amount of time.
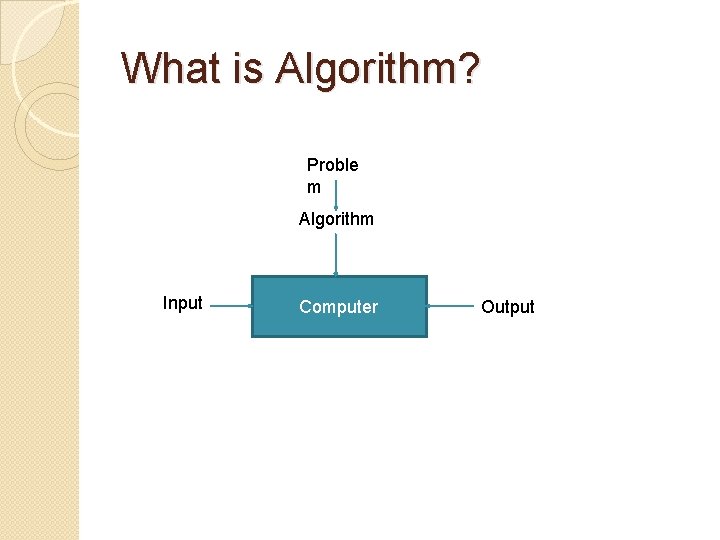
What is Algorithm? Proble m Algorithm Input Computer Output

Why DAA? �Computational Model? ◦ Idealized/ abstract description of real computers ◦ Specifies basic operations & rules to compose valid programs ◦ Why to measure complexity? ◦ If computers are infinitely fast & memory is free, do we have any reason to study algorithms? ◦ YES. To demonstrate our solution method terminates & does so with correct answer
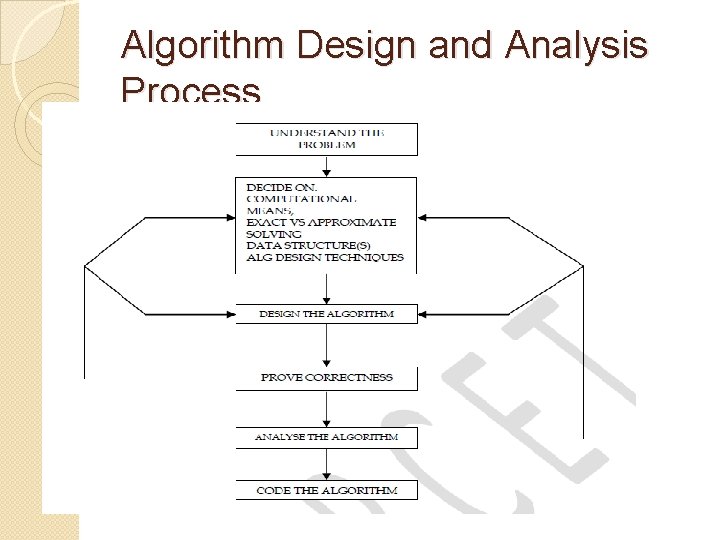
Algorithm Design and Analysis Process

Distinct areas of algorithms �How to devise algorithms �How to validate algorithms ◦ Program proving/verification �How to analyse algorithms �How to test programs

Analysis Framework �There are two kinds of efficiency ◦ Time efficiency - indicates how fast an algorithm in question runs. ◦ Space efficiency - deals with the extra space the algorithm requires. ◦ What to measure? How to measure?

Measuring an input size �An algorithm's efficiency as a function of some parameter n indicating the algorithm's input size. �For example, it will be the size of the list for problems of sorting, searching, finding the list's smallest element, and most other problems dealing with lists. �For the problem of evaluating a polynomial p(x) = an xn +. . . + a 0 of degree n ◦ It will be the polynomial's degree or the number of its coefficients �measuring size by the number b of bits in the n's binary representation: b= log 2 n +1

Measuring unit of running time? � In terms of a � Depends on secs, millisecs, …. . ◦ Speed of computer ◦ Quality of program ◦ Compiler � To get actual running time, need to have metric independent of above factors ◦ To count the number of times each of the algorithm's operations is executed. This approach is both difficult and unnecessary. ◦ To identify the most important operation of the algorithm, called the basic operation, the operation contributing the most to the total running time, and compute the number of times the basic operation is executed.

WORST CASE, BEST CASE AND AVERAGE CASE EFFICIENCES � Running time depends not only on an input size but also on the specifics of a particular input � Example- sequential search ALGORITHM Sequential Search(A[0. . n -1], K) //Searches for a given value in a given array by sequential search //Input: An array A[0. . n -1] and a search key K //Output: Returns the index of the first element of A that matches K // or -1 ifthere are no matching elements i← 0 while i < n and A[i] ≠ K do i←i+1 if i < n return i else return -1

WORST CASE, BEST CASE AND AVERAGE CASE EFFICIENCES �Worst case ◦ Cworst(n)=n for match found/nomatch found ◦ Guarantees that for any instance of size n, the running time will not exceed Cworst (n) its running time on the worst-case inputs. �Best case ◦ the first element equal to a search key; accordingly, Cbest(n) = 1.

WORST CASE, BEST CASE AND AVERAGE CASE EFFICIENCES �Worst case efficiency ◦ Efficiency for the worst-case input of size n for which the algorithm runs the longest among all possible inputs of that size. Cworst (n) = n it guarantees that for any instance of size n, the running time will not exceed C worst (n) its running time on the worst-case inputs.

�Average case efficiency ◦ information about an algorithm’s behaviour on a ‘typical’ and ‘random’ input. ◦ the average number of key comparisons made by sequential search is (n + 1) /2.

Insertion sort Algorithm 2. 1: INSERTION-SORT(A) 1 for j 2 to A. size do 2 key A[ j] // Insert A[ j] into the sorted sequence A[1. . j 1] 3 4 5 6 7 i← j-1 while i > 0 and A[i] > key do A[i + 1] ← A[i] i-A[i + 1] ← key
- Slides: 15