Descriptive Statistics A A Elimam B College of

Descriptive Statistics A. A. Elimam B. College of Business C. San Francisco State University

Statistics The Science of collecting, organizing, analyzing, interpreting and presenting data

Topics • Descriptive Statistics • Frequency Distributions and Histograms Relative / Cumulative Frequency • Measures of Central Tendency Mean, Median, Mode, Midrange

Topics • Measures of Dispersion (Variation) Range, Standard Deviation, Variance and Coefficient of variation • Shape Symmetric, Skewed, using Box-and. Whisker Plots • Quartile • Statistical Relationships Correlation , Covariance

Descriptive Statistics A collection of quantitative measures and ways of describing data. This includes: Frequency distributions & histograms, measures of central tendency and measures of dispersion

Descriptive Statistics • Collect Data e. g. Survey • Present Data e. g. Tables and Graphs • Characterize Data e. g. Mean A Characteristic of a: Population is a Parameter Sample is a Statistic.
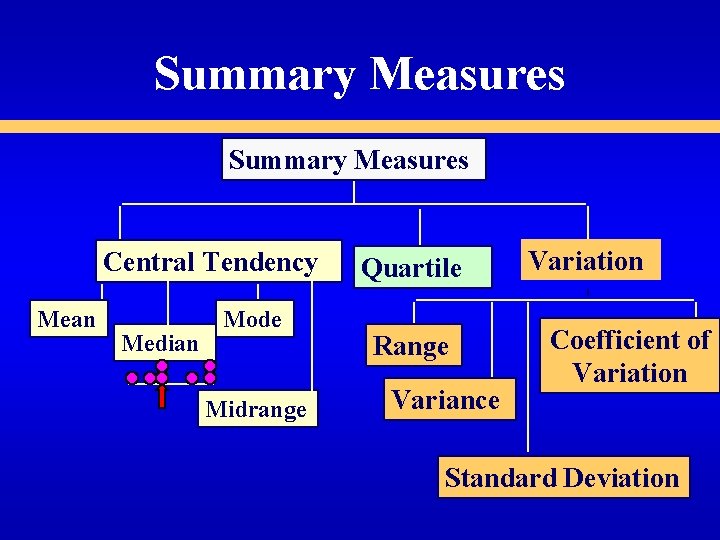
Summary Measures Central Tendency Mean Median Mode Midrange Quartile Range Variance Variation Coefficient of Variation Standard Deviation
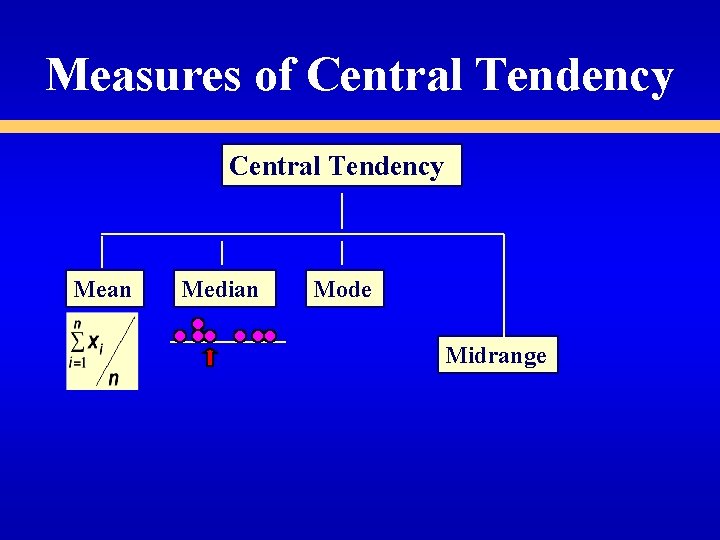
Measures of Central Tendency Mean Median Mode Midrange

The Mean (Arithmetic Average) • It is the Arithmetic Average of data values: Sample Mean • The Most Common Measure of Central Tendency • Affected by Extreme Values (Outliers) 0 1 2 3 4 5 6 7 8 9 10 Mean = 5 0 1 2 3 4 5 6 7 8 9 10 12 14 Mean = 6

The Median • Important Measure of Central Tendency • In an ordered array, the median is the “middle” number. • If n is odd, the median is the middle number. • If n is even, the median is the average of the 2 middle numbers. • Not Affected by Extreme Values 0 1 2 3 4 5 6 7 8 9 10 Median = 5 0 1 2 3 4 5 6 7 8 9 10 12 14 Median = 5

The Mode • A Measure of Central Tendency • Value that Occurs Most Often • Not Affected by Extreme Values • There May Not be a Mode • There May be Several Modes • Used for Either Numerical or Categorical Data 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Mode = 9 0 1 2 3 4 5 6 No Mode

Midrange • A Measure of Central Tendency • Average of Smallest and Largest Observation: Midrange • Affected by Extreme Value 0 1 2 3 4 5 6 7 8 9 10 Midrange = 5

Quartiles • Not a Measure of Central Tendency • Split Ordered Data into 4 Quarters 25% Q 1 25% Q 2 • Position of i-th Quartile: 25% Q 3 position of point Qi = i(n+1) 4 Data in Ordered Array: 11 12 13 16 16 17 18 21 22 Position of Q 1 = 1 • (9 + 1) 4 = 2. 50 Q 1 =12. 5

Quartiles • Not a Measure of Central Tendency • Split Ordered Data into 4 Quarters 25% Q 1 25% Q 2 • Position of i-th Quartile: 25% Q 3 position of point Qi = i(n+1) 4 Data in Ordered Array: 11 12 13 16 16 17 18 21 22 Position of Q 3 = 3 • (9 + 1) 4 = 7. 50 Q 3 =19. 5
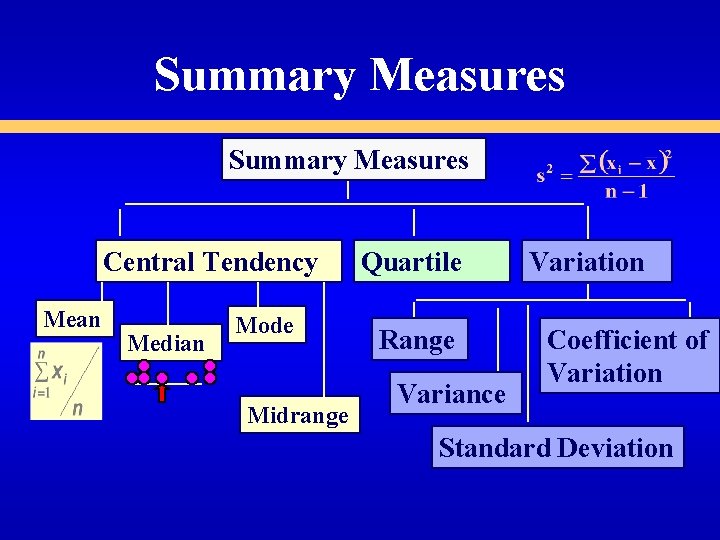
Summary Measures Central Tendency Mean Median Mode Midrange Quartile Range Variance Variation Coefficient of Variation Standard Deviation

Measures of Dispersion (Variation) Variation Variance Range Population Variance Sample Variance Standard Deviation Population Standard Deviation Sample Standard Deviation Coefficient of Variation

Understanding Variation • The more Spread out or dispersed data the larger the measures of variation • The more concentrated or homogenous the data the smaller the measures of variation • If all observations are equal measures of variation = Zero • All measures of variation are Nonnegative

The Range • Measure of Variation • Difference Between Largest & Smallest Observations: Range = • Ignores How Data Are Distributed: Range = 12 - 7 = 5 7 8 9 10 11 12

Variance • Important Measure of Variation • Shows Variation About the Mean: • For the Population: • For the Sample: For the Population: use N in the denominator. For the Sample : use n - 1 in the denominator.

Standard Deviation • Most Important Measure of Variation • Shows Variation About the Mean: • For the Population: • For the Sample: For the Population: use N in the denominator. For the Sample : use n - 1 in the denominator.

Sample Standard Deviation For the Sample : use n - 1 in the denominator. s Data: 10 12 n=8 s= = 4. 2426 14 15 17 18 Mean =16 18 24

Comparing Standard Deviations Data : 10 N= 8 s = 12 14 15 17 18 18 24 Mean =16 = 4. 2426 = 3. 9686 Value for the Standard Deviation is larger for data considered as a Sample.
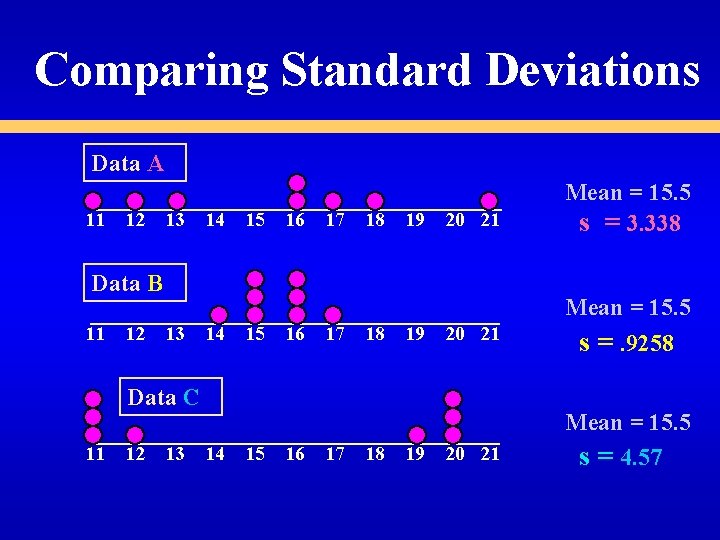
Comparing Standard Deviations Data A 11 12 13 14 15 16 17 18 19 20 21 Data B 11 12 13 14 15 16 17 18 19 20 21 Data C 11 12 13 14 15 16 17 18 19 20 21 Mean = 15. 5 s = 3. 338 Mean = 15. 5 s =. 9258 Mean = 15. 5 s = 4. 57

Coefficient of Variation • Measure of Relative Variation • Always a % • Shows Variation Relative to Mean • Used to Compare 2 or More Groups • Formula ( for Sample):

Comparing Coefficient of Variation Stock A: Average Price last year = $50 Standard Deviation = $5 Stock B: Average Price last year = $100 Standard Deviation = $5 Coefficient of Variation: Stock A: CV = 10% Stock B: CV = 5%

Shape • • Describes How Data Are Distributed Measures of Shape: Symmetric or skewed
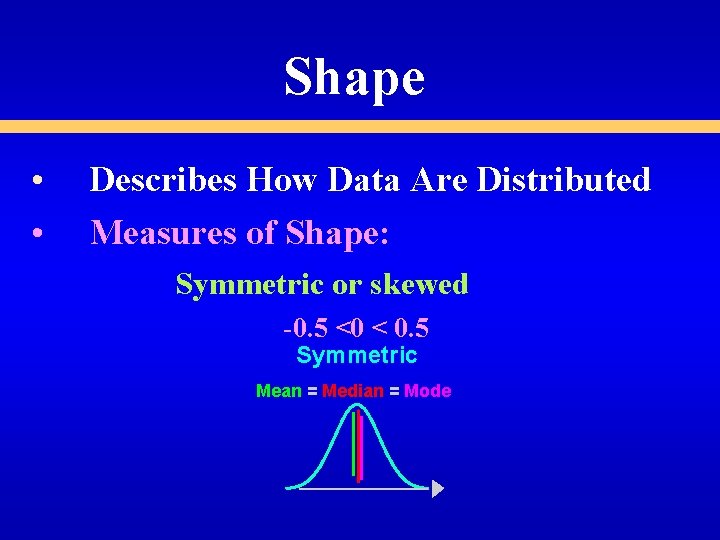
Shape • • Describes How Data Are Distributed Measures of Shape: Symmetric or skewed -0. 5 <0 < 0. 5 Symmetric Mean = Median = Mode
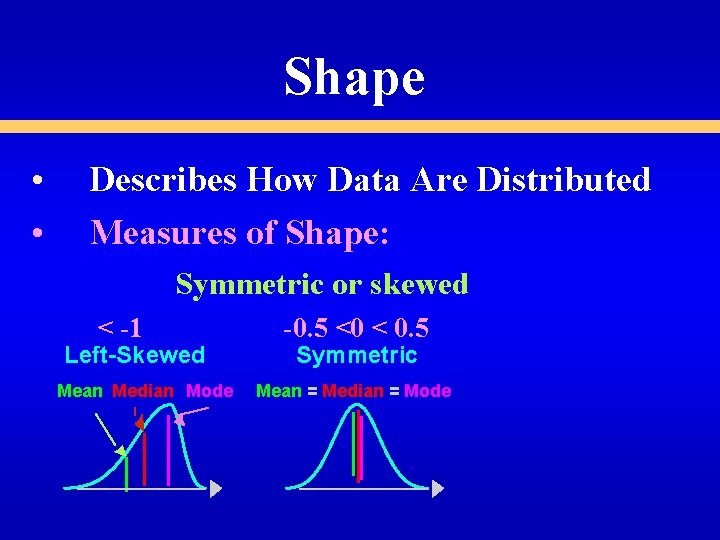
Shape • • Describes How Data Are Distributed Measures of Shape: Symmetric or skewed < -1 Left-Skewed Mean Median Mode -0. 5 <0 < 0. 5 Symmetric Mean = Median = Mode
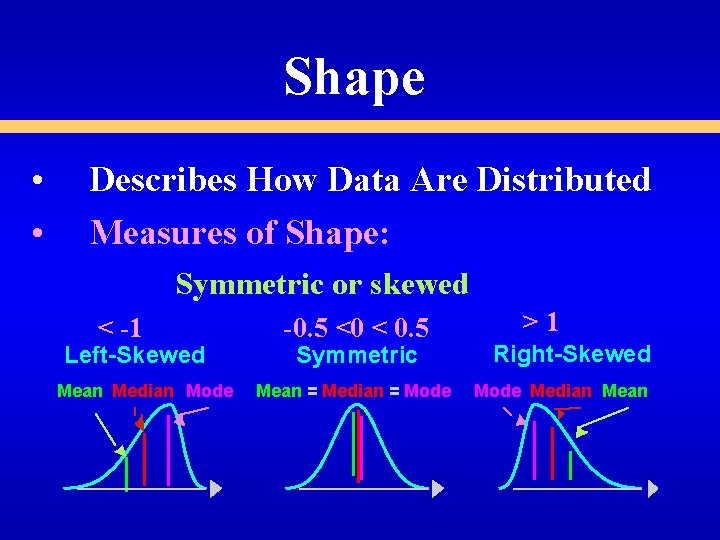
Shape • • Describes How Data Are Distributed Measures of Shape: Symmetric or skewed < -1 Left-Skewed Mean Median Mode -0. 5 <0 < 0. 5 Symmetric Mean = Median = Mode >1 Right-Skewed Mode Median Mean
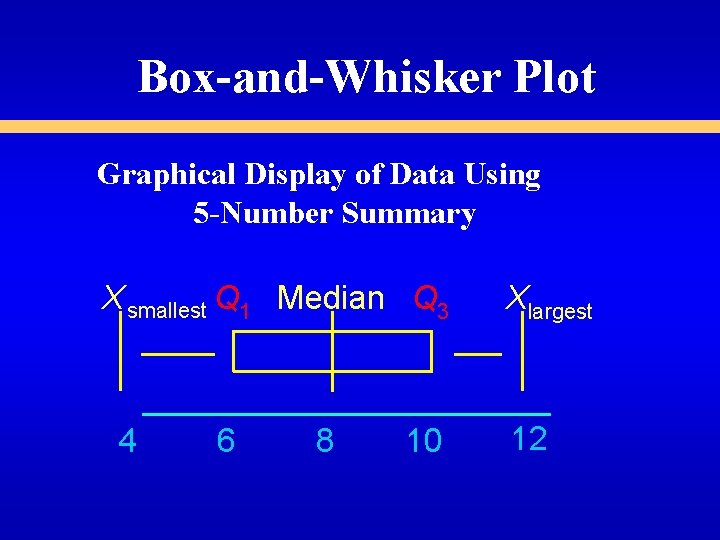
Box-and-Whisker Plot Graphical Display of Data Using 5 -Number Summary X smallest Q 1 Median Q 3 4 6 8 10 Xlargest 12
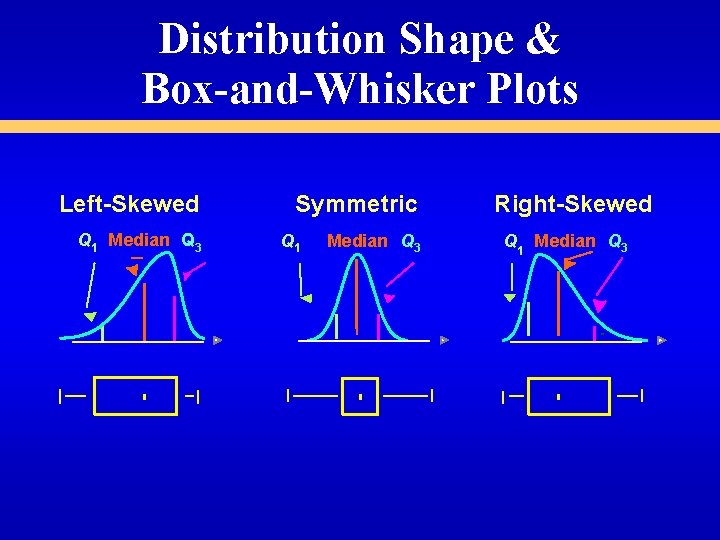
Distribution Shape & Box-and-Whisker Plots Left-Skewed Q 1 Median Q 3 Symmetric Q 1 Median Q 3 Right-Skewed Q 1 Median Q 3

Correlation A measure of the strength of linear relationship between two variables X and Y , and is measured by the (population) correlation coefficient: The numerator is the covariance

Covariance The average of the products of the deviations of each observation from its respective mean:

Sample Correlation Coefficient ranges from – 1 to +1 +1 perfect positive correlation 0 no linear correlation -1 perfect negative correlation

Summary • Discussed Measures of Central Tendency Mean, Median, Mode, Midrange • Quartiles • Addressed Measures of Variation The Range, Interquartile Range, Variance, Standard Deviation, Coefficient of Variation • Determined Shape of Distributions Symmetric, Skewed, Box-and-Whisker Plot Mean Median Mode Mean = Median = Mode Median Mean
- Slides: 35