Description logics Description Logics A family of KR

Description logics

Description Logics A family of KR formalisms, based on FOPL decidable, supported by automatic reasoning systems q Used for modelling of application domains q Classification of concepts and individuals concepts (unary predicates), subconcept (subsumption), roles (binary predicates), individuals (constants), constructors for building concepts, equality … [Baader et al. 2002] q

Applications software management n configuration management n natural language processing n clinical information systems n information retrieval n… n n Ontologies and the Web

Ontologies, Description Logics and OWL terminology Ontologies concept relation axiom instance DL concept role (binary) axiom individual OWL class property axiom individual

Outline n DL languages ¨ n syntax and semantics DL reasoning services ¨ algorithms, complexity DL systems n DLs for the web n

DL SYNTAX

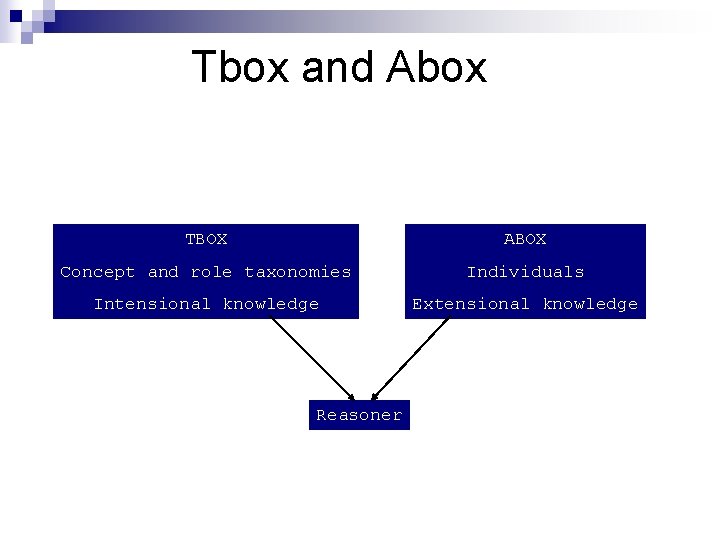
Tbox and Abox TBOX ABOX Concept and role taxonomies Individuals Intensional knowledge Extensional knowledge Reasoner

AL R atomic role, A atomic concept C, D A | (atomic concept) T | (universal concept, top) owl: thing | (bottom concept) owl: nothing A | (atomic negation) owl: complement. Of C D | (conjunction) owl: intersection. Of R. C | (value restriction) owl: all. Values. From R. T (limited existential quantification) owl: some. Values. From

AL[X] C C (concept negation) owl: complement. Of U C U D (disjunction) owl: union. Of E R. C (existential quantification) owl: some. Values. From N ≥ n R, ≤ n R (number restriction) Q owl: max. Cardinality, owl: min. Cardinality ≥ n R. C, ≤ n R. C (qualified number restriction) owl: max. Qualified. Cardinality, owl: min. Qualified. Cardinality

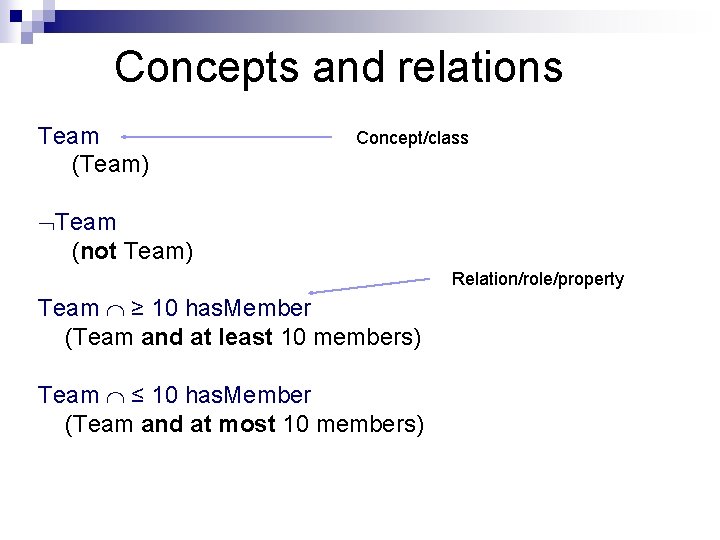
Concepts and relations Team (Team) Concept/class Team (not Team) Relation/role/property Team ≥ 10 has. Member (Team and at least 10 members) Team ≤ 10 has. Member (Team and at most 10 members)

Concepts and relations Team has. Member. Football-player (Team and all members are football players) Team has. Member. Football-player (Team and there is a member that is a football player)

AL[X] R R S (role conjunction) I R- (inverse roles) H (role hierarchies) F u 1 = u 2, u 1 ≠ u 2 (feature (dis)agreements)

S[X] S ALC + transitive roles SHIQ ALC + transitive roles + role hierarchies + inverse roles + number restrictions

Tbox n Terminological axioms: ¨ C = D (R = S) owl: equivalent. Class / owl: equivalent. Property Football-player Athlete (Every football player is an athlete) (R S) rdfs: sub. Class. Of / rdfs: sub. Property. Of ¨ (disjoint C D) owl: disjoint. With ¨ C D

Tbox An equality whose left-hand side is an atomic concept is a definition. n A finite set of definitions T is a Tbox (or terminology) if no symbolic name is defined more than once. n

Example Team ≥ 2 has. Member Large-Team = Team ≥ 10 has. Member Sports-team = Team has. Member. Athlete Football-Team = Team ≥ 11 has. Member. Football-player Athlete

DL as sublanguage of FOPL Team(this) ^ ( x 1, . . . , x 11: has. Member(this, x 1) ^ … ^ has. Member(this, x 11) ^ x 1 ≠ x 2 ^ … ^ x 10 ≠ x 11) ^ ( x: has. Member(this, x) Football-player(x))

Abox n Assertions about individuals: ¨ C(a) ¨ R(a, b)

Example Football-Team(Real_Madrid) has. Member(Real_Madrid, Eden_Hazard)

Knowledge base A knowledge base is a tuple < T, A > where T is a Tbox and A is an Abox.

Example Team ≥ 2 has. Member Large-Team = Team ≥ 10 has. Member Sports-team = Team has. Member. Athlete Football-Team = Team ≥ 11 has. Member. Football-player Athlete Football-Team(Real_Madrid) has. Member(Real_Madrid, Eden_Hazard)

Example - OWL <Declaration> <Object. Property IRI="#hasmember"/> </Declaration> <Declaration> <Declaration> <Class IRI="#football-player"/> </Declaration> <Class IRI="#athlete"/> </Declaration> <Class IRI="#team"/> </Declaration> <Class IRI="#large-team"/> </Declaration> <Class IRI="#sports-team"/> </Declaration> <Class IRI="#football-team"/> </Declaration> <Named. Individual IRI="#Real_Madrid"/> </Declaration> <Named. Individual IRI="#Eden_Hazard"/> </Declaration>

Example - OWL Large-Team = Team ≥ 10 has. Member <Equivalent. Classes> <Class IRI="#large-team"/> <Object. Intersection. Of> <Class IRI="#team"/> <Object. Min. Cardinality cardinality="10"> <Object. Property IRI="#hasmember"/> </Object. Min. Cardinality> </Object. Intersection. Of> </Equivalent. Classes>

Example - OWL Football-Team = Team ≥ 11 has. Member. Football-player <Equivalent. Classes> <Class IRI="#football-team"/> <Object. Intersection. Of> <Class IRI="#team"/> <Object. All. Values. From> <Object. Property IRI="#hasmember"/> <Class IRI="#football-player"/> </Object. All. Values. From> <Object. Min. Cardinality cardinality="11"> <Object. Property IRI="#hasmember"/> </Object. Min. Cardinality> </Object. Intersection. Of> </Equivalent. Classes>

DL SEMANTICS

AL (Semantics) An interpretation I consists of a non-empty set I (the domain of the interpretation) and an interpretation function. I which assigns to every atomic concept A a set AI I and to every atomic role R a binary relation RI I I. The interpretation function is extended to concept definitions using inductive definitions.

AL (Semantics) C, D A | (atomic concept) T | (universal concept) TI = I | (bottom concept) I = Ø A | (atomic negation) ( A)I = I AI C D | (conjunction) (C D)I = CI DI R. C | (value restriction) ( R. C)I = {a I| b. (a, b) RI b CI } R. T | (limited existential ( R. T)I = {a I| b. (a, b) RI} quantification)

ALC (Semantics) ( C)I = I CI (C U D)I = CI U DI (≥ n R)I = {a I| # {b I | (a, b) RI } ≥ n } (≤ n R)I = {a I| # {b I | (a, b) RI } ≤ n } ( R. C)I = {a I| b I : (a, b) RI ^ b CI}

Semantics Individual i i. I I Unique Name Assumption: if i 1 ≠ i 2 then i 1 I ≠ i 2 I

Semantics An interpretation. I is a model for a terminology T iff CI = DI for all C = D in T CI DI for all a C D in T CI DI = Ø for all (disjoint C D) in T

Semantics An interpretation. I is a model for a knowledge base <T, A > iff. I is a model for T a. I CI for all C(a) in A <a. I, b. I> RI for all R(a, b) in A

Semantics - acyclic Tbox Bird = Animal Skin. Feather I = {tweety, goofy, fea 1, fur 1} Animal. I = {tweety, goofy} Feather. I = {fea 1} Skin. I = {<tweety, fea 1>, <goofy, fur 1>} Bird. I = {tweety}

Exercise Create an interpretation for: Team ≥ 2 has. Member Large-Team = Team ≥ 10 has. Member Sports-team = Team has. Member. Athlete Football-Team = Team ≥ 11 has. Member. Football-player Athlete Football-Team(Real_Madrid) has. Member(Real_Madrid, Eden_Hazard)

Semantics - cyclic Tbox Quiet. Person = Person Friend. Quiet. Person ( A = F(A) ) I = {john, sue, andrea, bill} Person. I = {john, sue, andrea, bill} Friend. I = {<john, sue>, <andrea, bill>, <bill, bill>} Quiet. Person. I ={john, sue, andrea, bill}

Semantics - cyclic Tbox Descriptive semantics: A = F(A) is a constraint stating that A has to be some solution for the equation. n Not appropriate for defining concepts n Necessary and sufficient conditions for concepts Human = Mammal Parent. Human

Semantics - cyclic Tbox Least fixpoint semantics: A = F(A) specifies that A is to be interpreted as the smallest solution (if it exists) for the equation. n Appropriate for inductively defining concepts DG = Empty. DG U Non-Empty-DG = Node Arc. Non-Empty-DG Human = Mammal Parent. Human =

Semantics - cyclic Tbox Greatest fixpoint semantics: A = F(A) specifies that A is to be interpreted as the greatest solution (if it exists) for the equation. n Appropriate for defining concepts whose individuals have circularly repeating structure Fo. B = Blond Child. Fo. B Human = Mammal Parent. Human Horse = Mammal Parent. Horse Human = Horse

Open world vs closed world semantics Databases: closed world reasoning database instance represents one interpretation absence of information interpreted as negative information “complete information” query evaluation is finite model checking DL: open world reasoning Abox represents many interpretations (its models) absence of information is lack of information “incomplete information” query evaluation is logical reasoning

Open world vs closed world semantics has. Child(Jocasta, Oedipus) has. Child(Jocasta, Polyneikes) has. Child(Oedipus, Polyneikes) has. Child(Polyneikes, Thersandros) patricide(Oedipus) patricide(Thersandros) (not represented in DB) Does it follow from the Abox that has. Child. (patricide has. Child. patricide)(Jocasta) ?

DL REASONING

Example Teams have at least two members, while large teams have at least 10 members. Sports teams are teams which have only athletes as members. A football team is a team which has at least 11 members and all the members are football players. Football players are athletes. Real Madrid is a football team that has Eden Hazard as a member.

Example Team ≥ 2 has. Member Large-Team = Team ≥ 10 has. Member Sports-team = Team has. Member. Athlete Football-Team = Team ≥ 11 has. Member. Football-player Athlete Football-Team(Real_Madrid) has. Member(Real_Madrid, Eden_Hazard)

Example Every team has at least 2 members Every large team is a team and has at least 10 members Every sports team is a team and has only athletes as members Every football team is a team and has at least 11 members and has only football players as members

Example Every team has at least 2 members Every large team is a team and has at least 10 members Every sports team is a team and has only athletes as members Every football team is a team and has at least 11 members and has only football players as members Reasoning: Every football team is a large team Every football team is a sports team

Example Real Madrid is an instance of football team Real Madrid has member Eden Hazard

Reasoning: Example Real Madrid is an instance of football team Real Madrid is an instance of large team Real Madrid is an instance of sports team Real Madrid has at least 11 members All members in Real Madrid are football players All members in Real Madrid are athletes Real Madrid has member Eden Hazard is an instance of football player Eden Hazard is an instance of athlete

Reasoning services n Satisfiability of concept Subsumption between concepts Equivalence between concepts Disjointness of concepts n Classification n Instance checking Realization Retrieval Knowledge base consistency n n n

Reasoning services n Satisfiability of concept ¨ n Subsumption between concepts ¨ n C is subsumed by D w. r. t. T if CI DI for every model I of T. Equivalence between concepts ¨ n C is satisfiable w. r. t. T if there is a model I of T such that CI is not empty. C is equivalent to D w. r. t. T if CI = DI for every model I of T. Disjointness of concepts ¨ C and D are disjoint w. r. t. T if CI DI = Ø for every model I of T.

Reasoning services n Reduction to subsumption is unsatisfiable iff C is subsumed by ¨ C and D are equivalent iff C is subsumed by D and D is subsumed by C ¨C ¨C n and D are disjoint iff C D is subsumed by The statements also hold w. r. t. a Tbox.

Reasoning services n Reduction to unsatisfiability ¨ C is subsumed by D iff C D is unsatisfiable ¨C and D are equivalent iff both (C D) and (D C) are unsatisfiable ¨ C and D are disjoint iff C D is unsatisfiable n The statements also hold w. r. t. a Tbox.

Tableau algorithms n To prove that C subsumes D: If C subsumes D, then it is impossible for an individual to belong to D but not to C. ¨ Idea: Create an individual that belongs to D and not to C and see if it causes a contradiction. ¨ If always a contradiction (clash) then subsumption is proven. Otherwise, we have found a model that contradicts the subsumption. ¨

Tableau algorithms n Based on constraint systems. = { x: C D } ¨ Add constraints according to a set of propagation rules ¨ Until clash or no constraint is applicable ¨S

Tableau algorithms – de Morgan rules C C (A B) A U B (A U B) A B ( R. C) R. ( C)

Tableau algorithms – constraint propagation rules n S {x: C 1, x: C 2} U S if x: C 1 C 2 in S and either x: C 1 or x: C 2 is not in S U {x: D} U S if x: C 1 U C 2 in S and neither x: C 1 or x: C 2 is in S, and D = C 1 or D = C 2

Tableau algorithms – constraint propagation rules n S {y: C} U S if x: R. C in S and x. Ry in S and y: C is not in S {x. Ry, y: C} U S if x: R. C in S and y is a new variable and there is no z such that both x. Rz and z: C are in S

Example ST: Tournament has. Participant. Swedish n SBT: Tournament has. Participant. (Swedish Belgian) n

Example 1 SBT => ST? n S = { x: (Tournament has. Participant. Swedish) (Tournament has. Participant. (Swedish Belgian)) } n

Example 1 n S = { x: ( Tournament U has. Participant. Swedish) (Tournament has. Participant. (Swedish Belgian)) }

Example 1 -rule: n S={ x: ( Tournament U has. Participant. Swedish) (Tournament has. Participant. (Swedish Belgian)), x: Tournament U has. Participant. Swedish, x: Tournament, x: has. Participant. (Swedish Belgian) }

Example 1 -rule: n S={ x: ( Tournament U has. Participant. Swedish) (Tournament has. Participant. (Swedish Belgian)), x: Tournament U has. Participant. Swedish, x: Tournament, x: has. Participant. (Swedish Belgian), x has. Participant y, y: (Swedish Belgian) }

Example 1 -rule: n ( Tournament U has. Participant. Swedish) (Tournament has. Participant. (Swedish Belgian)), x: Tournament U has. Participant. Swedish, x: Tournament, x: has. Participant. (Swedish Belgian), x has. Participant y, y: (Swedish Belgian), y: Swedish, y: Belgian } S= {x:

Example 1 U-rule, choice 1 n S = { x: ( Tournament U has. Participant. Swedish) (Tournament has. Participant. (Swedish Belgian)), x: Tournament U has. Participant. Swedish, x: Tournament, x: has. Participant. (Swedish Belgian), x has. Participant y, y: (Swedish Belgian), y: Swedish, y: Belgian, x: Tournament } clash

Example 1 U-rule, choice 2 n S = {x: ( Tournament U has. Participant. Swedish) (Tournament has. Participant. (Swedish Belgian)), x: Tournament U has. Participant. Swedish, x: Tournament, x: has. Participant. (Swedish Belgian), x has. Participant y, y: (Swedish Belgian), y: Swedish, y: Belgian, x: has. Participant. Swedish }

Example 1 choice 2 – continued -rule S={ x: ( Tournament U has. Participant. Swedish) (Tournament has. Participant. (Swedish Belgian)), x: Tournament U has. Participant. Swedish, x: Tournament, x: has. Participant. (Swedish Belgian), x has. Participant y, y: (Swedish Belgian), y: Swedish, y: Belgian, x: has. Participant. Swedish, y: Swedish } n clash

Example 2 ST => SBT? n S = { x: (Tournament has. Participant. (Swedish Belgian)) (Tournament has. Participant. Swedish) } n

Example 2 n S = { x: ( Tournament U has. Participant. ( Swedish U Belgian)) (Tournament has. Participant. Swedish) }

Example 2 -rule n S={ x: ( Tournament U has. Participant. ( Swedish U Belgian)) (Tournament has. Participant. Swedish), x: ( Tournament U has. Participant. ( Swedish U Belgian)), x: Tournament, x: has. Participant. Swedish }

Example 2 -rule n S={ x: ( Tournament U has. Participant. ( Swedish U Belgian)) (Tournament has. Participant. Swedish), x: ( Tournament U has. Participant. ( Swedish U Belgian)), x: Tournament, x: has. Participant. Swedish, x has. Participant y, y: Swedish }

Example 2 U –rule, choice 1 n S={ x: ( Tournament U has. Participant. ( Swedish U Belgian)) (Tournament has. Participant. Swedish), x: ( Tournament U has. Participant. ( Swedish U Belgian)), x: Tournament, x: has. Participant. Swedish, x has. Participant y, y: Swedish, x: Tournament } clash

Example 2 U –rule, choice 2 n S={ x: ( Tournament U has. Participant. ( Swedish U Belgian)) (Tournament has. Participant. Swedish), x: ( Tournament U has. Participant. ( Swedish U Belgian)), x: Tournament, x: has. Participant. Swedish, x has. Participant y, y: Swedish, x: has. Participant. ( Swedish U Belgian) }

Example 2 choice 2 continued –rule n S={ x: ( Tournament U has. Participant. ( Swedish U Belgian)) (Tournament has. Participant. Swedish), x: ( Tournament U has. Participant. ( Swedish U Belgian)), x: Tournament, x: has. Participant. Swedish, x has. Participant y, y: Swedish, x: has. Participant. ( Swedish U Belgian), y: ( Swedish U Belgian) }

Example 2 choice 2 continued U–rule, choice 2. 1 n S={ x: ( Tournament U has. Participant. ( Swedish U Belgian)) (Tournament has. Participant. Swedish), x: ( Tournament U has. Participant. ( Swedish U Belgian)), x: Tournament, x: has. Participant. Swedish, x has. Participant y, y: Swedish, x: has. Participant. ( Swedish U Belgian), y: Swedish } clash

Example 2 choice 2 continued U–rule, choice 2. 2 n S={ x: ( Tournament U has. Participant. ( Swedish U Belgian)) (Tournament has. Participant. Swedish), x: ( Tournament U has. Participant. ( Swedish U Belgian)), x: Tournament, x: has. Participant. Swedish, x has. Participant y, y: Swedish, x: has. Participant. ( Swedish U Belgian), y: Belgian } ok, model

Complexity - languages n Overview available via the DL home page at http: //dl. kr. org Example tractable language: A, T, , A, C D, R. C, ≥ n R, ≤ n R Reasons for intractability: choices, e. g. C U D exponential size models, e. g interplay universal and existential quantification Reasons for undecidability: e. g. role-value maps R=S

DL SYSTEMS

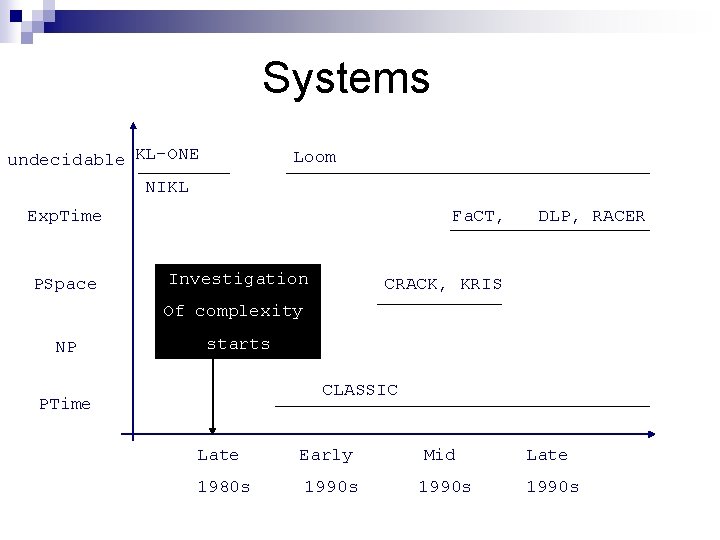
Systems undecidable KL-ONE NIKL Loom Exp. Time PSpace Fa. CT, Investigation DLP, RACER CRACK, KRIS Of complexity NP starts CLASSIC PTime Late 1980 s Early 1990 s Mid 1990 s Late 1990 s

Systems Overview available via the DL home page at http: //dl. kr. org n Current systems include: CEL, Cerebra Enginer, Fa. CT++, fuzzy. DL, Hermi. T, KAON 2, MSPASS, Pellet, Qu. Onto, Racer. Pro, SHER n

Extensions Time n Defaults n Part-of n Knowledge and belief n Uncertainty (fuzzy, probabilistic) n

DL AND THE WEB

OWL n n n OWL-Lite, OWL-DL, OWL-Full: increasing expressivity A legal OWL-Lite ontology is a legal OWL-DL ontology is a legal OWL-Full ontology OWL-DL: expressive description logic, decidable XML-based RDF-based (OWL-Full is extension of RDF, OWLLite and OWL-DL are extensions of a restriction of RDF)

OWL-Lite n n n n Class, sub. Class. Of, equivalent. Class intersection. Of (only named classes and restrictions) Property, sub. Property. Of, equivalent. Property domain, range (global restrictions) inverse. Of, Transitive. Property (*), Symmetric. Property, Functional. Property, Inverse. Functional. Property all. Values. From, some. Values. From (local restrictions) min. Cardinality, max. Cardinality (only 0/1) Individual, same. As, different. From, All. Different (*) restricted

OWL-DL n n n n n Type separation (class cannot also be individual or property, property cannot be also class or individual), Separation between Datatype. Properties and Object. Properties Class –complex classes, sub. Class. Of, equivalent. Class, disjoint. With intersection. Of, union. Of, complement. Of Property, sub. Property. Of, equivalent. Property domain, range (global restrictions) inverse. Of, Transitive. Property (*), Symmetric. Property, Functional. Property, Inverse. Functional. Property all. Values. From, some. Values. From (local restrictions), one. Of, has. Value min. Cardinality, max. Cardinality Individual, same. As, different. From, All. Different (*) restricted

OWL 2 n OWL 2 Full and OWL 2 DL compatible with SROIQ n Punning n ¨ IRI may denote both class and individual ¨ For reasoning they are considered separate entities

OWL 2 n profiles OWL 2 EL (based on EL++) ¨ Essentially intersection and existential quantification ¨ SNOMED CT, NCI Thesaurus n OWL 2 QL (“query language”) ¨ Can be realized using relational database technology ¨ RDFS + small extensions n OWL 2 RL (“rule language”)

References n n n Baader, Calvanese, Mc. Guinness, Nardi, Patel. Schneider. The Description Logic Handbook. Cambridge University Press, 2003. Donini, Lenzerini, Nardi, Schaerf, Reasoning in description logics. Principles of knowledge representation. CSLI publications. pp 191 -236. 1996. dl. kr. org

References n https: //www. w 3. org/TR/2004/REC-owl-features 20040210/ n https: //www. w 3. org/TR/2012/REC-owl 2 -quickreference-20121211/ https: //www. w 3. org/TR/2012/REC-owl 2 -primer 20121211/ n