Descrierea matematica a sistemelor dinamice Ce sunt modelele

Descrierea matematica a sistemelor dinamice Ce sunt modelele matematice? Cunoasterea stiintifica se bazeaza pe doua categorii de metode: • Metode experimentale • Metode de modelare Metodele experimentale implica interactiunea directa cu obiectul de studiu si au, in unele cazuri, aplicabilitate limitata. Sistemele reale asupra carora se pot face observatii experimentale sunt, principial modelabile. Experimentele care nu pot fi realizate cu sistemele reale pot fi facute pe modelele respectivelor sisteme.

Avantajul cunoasterii modelelor matematice • Intelegerea sistemelor si a functionarii acestora; – Sub aspect fenomenologic – Sub aspect relational canitativ Este necesar sa se analizeze relatiile dintre variabilele unui sistem si sa se scrie ecuatiile corespunzatoare

Sistemele evolueaza in timp Sunt sisteme dinamice Relatiile dintre variabile au forma unor ecuatii diferentiale si/sau integro -diferentiale. Ecuatiile pot fi: • Liniare • Liniarizabile (transformata Laplace)

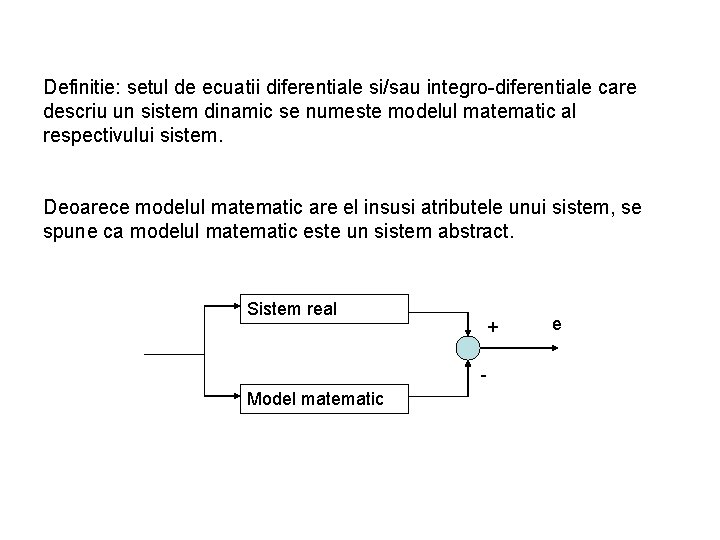
Definitie: setul de ecuatii diferentiale si/sau integro-diferentiale care descriu un sistem dinamic se numeste modelul matematic al respectivului sistem. Deoarece modelul matematic are el insusi atributele unui sistem, se spune ca modelul matematic este un sistem abstract. Sistem real + - Model matematic e

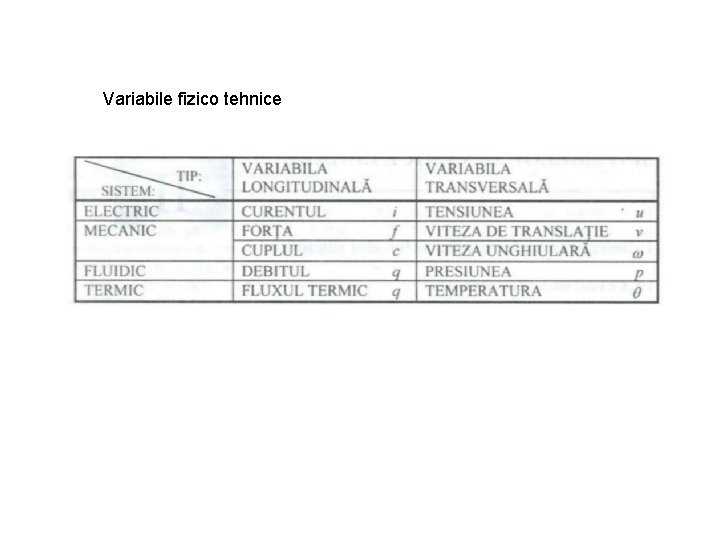
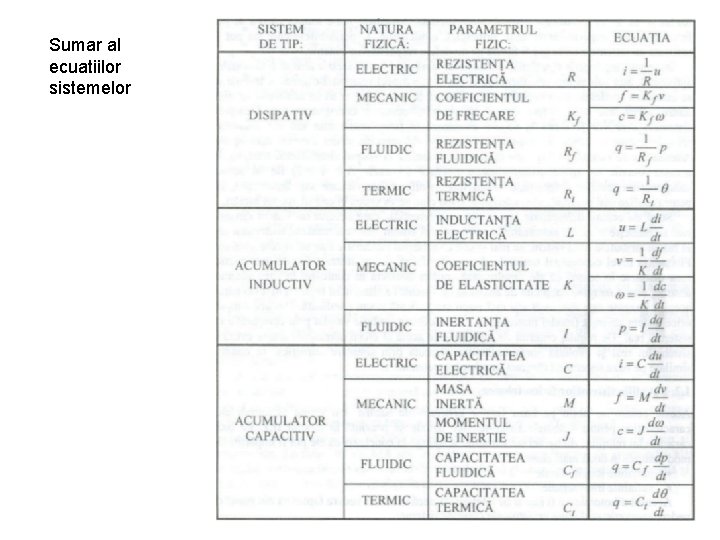
Ecuatiile sistemelor fizico-tehnice Se obtin pe baza legilor generale naturii Variabilele pot fi impartite in doua clase: variabile longitudinale variabile transversale Din punct de vedere energetic se disting urmatoarele clase de sisteme: sisteme disipative sisteme cu acumulare inductiva sisteme cu acumulare capacitiva

Variabile fizico tehnice

Sumar al ecuatiilor sistemelor

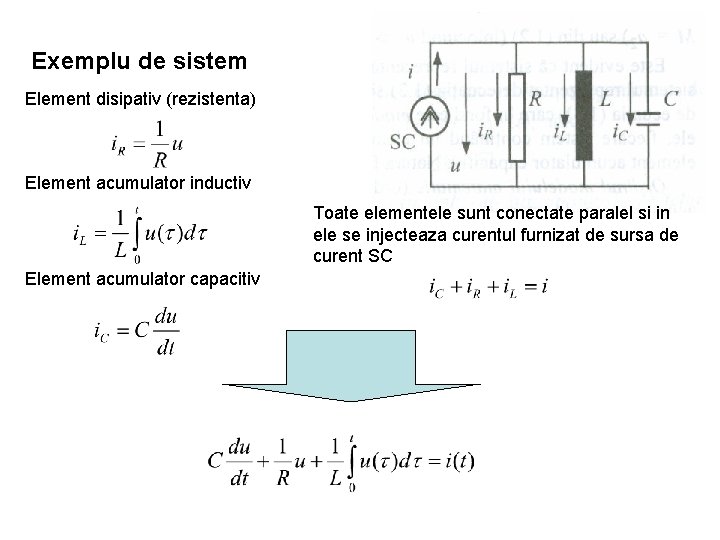
Exemplu de sistem Element disipativ (rezistenta) Element acumulator inductiv Toate elementele sunt conectate paralel si in ele se injecteaza curentul furnizat de sursa de curent SC Element acumulator capacitiv

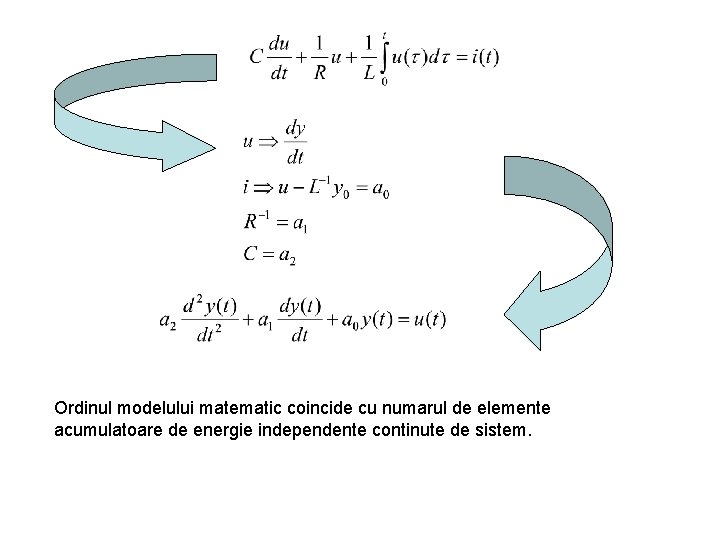
Ordinul modelului matematic coincide cu numarul de elemente acumulatoare de energie independente continute de sistem.

Liniaritate si invarianta in timp Marea majoritate a sistemelor reale au o comportare liniara in domenii de variatie ale variabilelor bine precizate sau precizabile. Pentru formalizarea proprietatii de liniaritate se are in vedere ca un sistem materializeaza relatia dintre marimea de intrare si marimea de iesire. u(t) SISTEM y(t)

DEFINITII Definitia 1 Sistemul anterior este liniar daca pentru orice constante reale c 1 si c 2 marimea de intrare se transfera in

DEFINITII Definitia 2 Sistemul anterior se numeste neted si cu parametri concentrati daca el este reprezentat de o ecuatie sau un set de ecuatii diferentiale ordinare. Definitia 3 Sistemul anterior se numeste invariant in timp daca toti parametrii sai sunt invarianti in timp

FUNCTIA DE TRANSFER In general, un sistem dinamic neted, cu parametri concentrati, liniar si invariant in timp, cu o singura marime de intrare si o singura marime de iesire (ambele functii scalare de timp, motiv pentru care sistemul se mai numeste si sistem monovariabil) este descris de o ecuatie diferentiala ordinara, liniara, cu coeficienti constanti, de forma: Numerele n si m sunt corelate cu numarul de elemente acumulatoare de energie, independente intre ele, continute de sistem.

Pentru fixarea cadrului tratarii si in conformitate cu definitia transformarii Laplace, se admite ca pana la momentul initial t 0 = 0 sistemul anterior se afla in repaus, adica: In conformitate cu principiul cauzalitatii, acest lucru se mai exprima astfel: cauza nula produce efectul nul. In conformitate cu principiul non-anticiparii, acest lucru se mai exprima astfel: efectul nu anticipeaza cauza. DEFINITIA 4 Un sistem care satisface ecuatia de mai sus se numeste non-anticipativ. In caz contrar, se numeste anticipativ. In lumea reala, sistemele naturale sau fizico-tehnice, sunt non-anticipative.

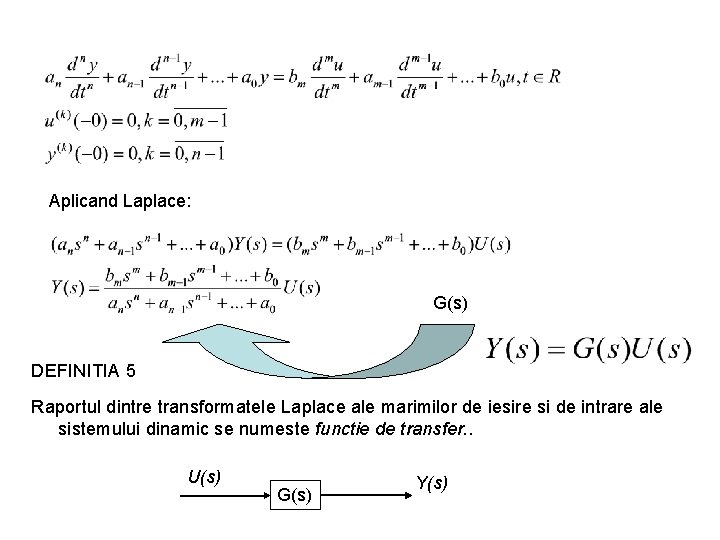
Aplicand Laplace: G(s) DEFINITIA 5 Raportul dintre transformatele Laplace ale marimilor de iesire si de intrare ale sistemului dinamic se numeste functie de transfer. . U(s) G(s) Y(s)

Cauza U(s) apare in membrul drept, iar Y(s) apare in membrul stang, evidentiindu-se astfel faptul ca Y(s) este rezultatul actiunii lui U(s) prin intermediul lui G(s). Functia de transfer G(s) este o fractie rationala de variabila complexa s. Functia de transfer nu depinde nici de marimea de intrare, nici de cea de iesire ci numai de structura si parametrii sistemului insusi. DEFINITIA 6 Polinomul zerourilor Polinomul polilor DEFINITIA 7 Daca o functie rationala satisface m<n atunci se numeste strict proprie. In caz contrar, ea se numeste proprie (m=n) sau improprie (m>n).

Scheme bloc structurale Modelul matematic este rezultatul unei proceduri care la debut are caracter analitic. Acest caracter deriva din aplicarea metodei analitice ca metoda de investigare. Aplicarea metodei analitice: • Impartirea sistemului analizat in elementele sale componente cele mai simple; • Studiul lor separat; • Descrierea matematica a fenomenelor conform legilor care le guverneaza; • Evidentierea marimilor cauze si efecte pentru fiecare element in parte; • Daca elementele sunt liniare, se aplica Laplace, asociindu-se fiecarui element cate o schema bloc partiala Prin reunirea adecvata a tuturor schemelor bloc partiale, in cadrul unei operatii de sinteza, bazata pe conexiunile existente intre elemente, se obtine schema bloc structurala a sistemului analizat.

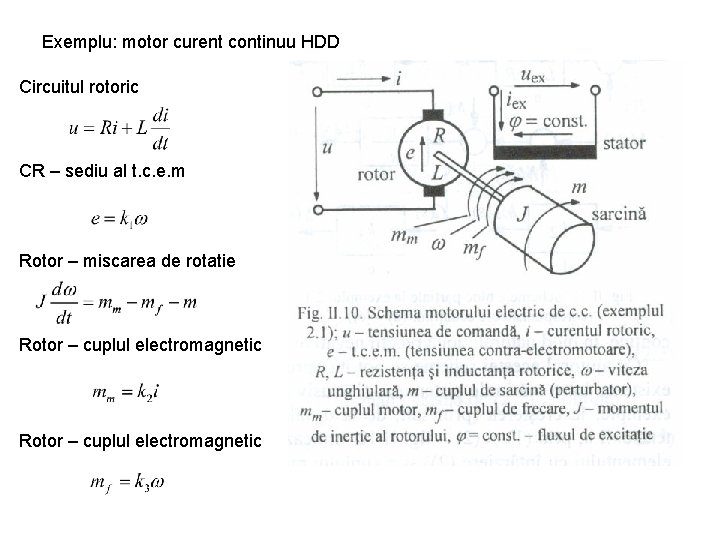
Exemplu: motor curent continuu HDD Circuitul rotoric CR – sediu al t. c. e. m Rotor – miscarea de rotatie Rotor – cuplul electromagnetic

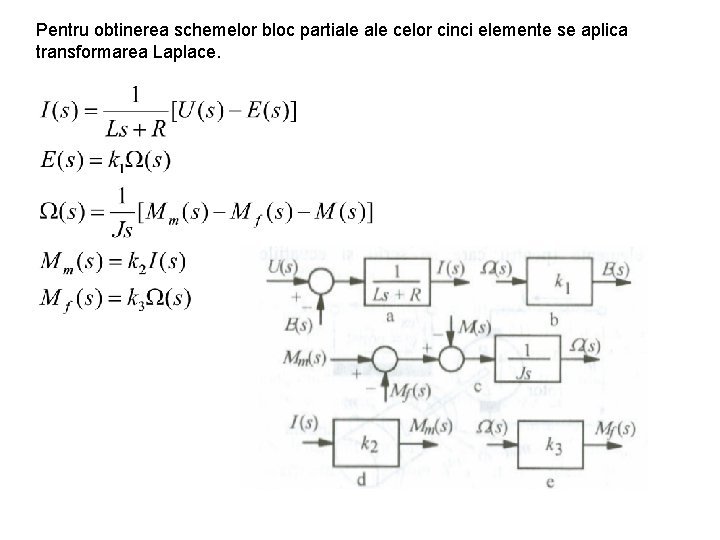
Pentru obtinerea schemelor bloc partiale celor cinci elemente se aplica transformarea Laplace.

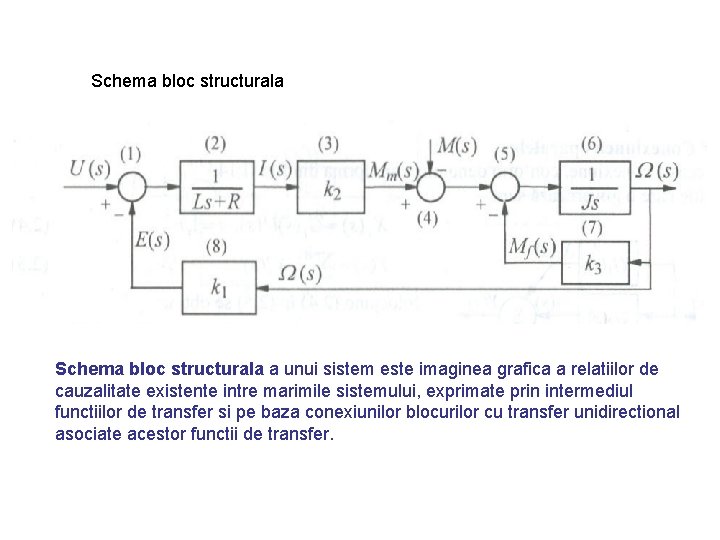
Schema bloc structurala a unui sistem este imaginea grafica a relatiilor de cauzalitate existente intre marimile sistemului, exprimate prin intermediul functiilor de transfer si pe baza conexiunilor blocurilor cu transfer unidirectional asociate acestor functii de transfer.

Conexiuni elementare Conexiunea serie Functia de transfer echivalenta a conexiunii serie este egala cu produsul functiilor de transfer ale elementelor componente.

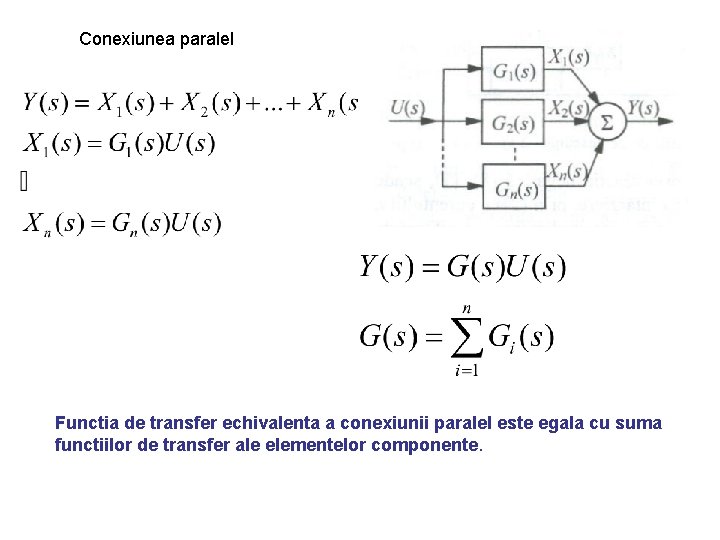
Conexiunea paralel Functia de transfer echivalenta a conexiunii paralel este egala cu suma functiilor de transfer ale elementelor componente.

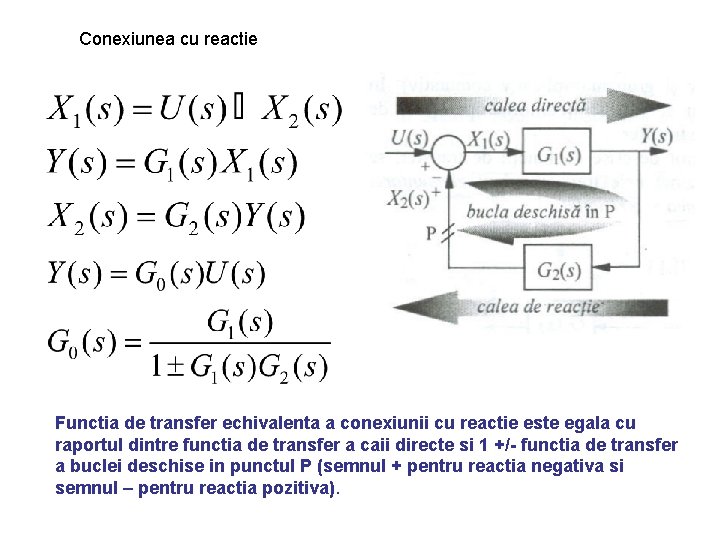
Conexiunea cu reactie Functia de transfer echivalenta a conexiunii cu reactie este egala cu raportul dintre functia de transfer a caii directe si 1 +/- functia de transfer a buclei deschise in punctul P (semnul + pentru reactia negativa si semnul – pentru reactia pozitiva).

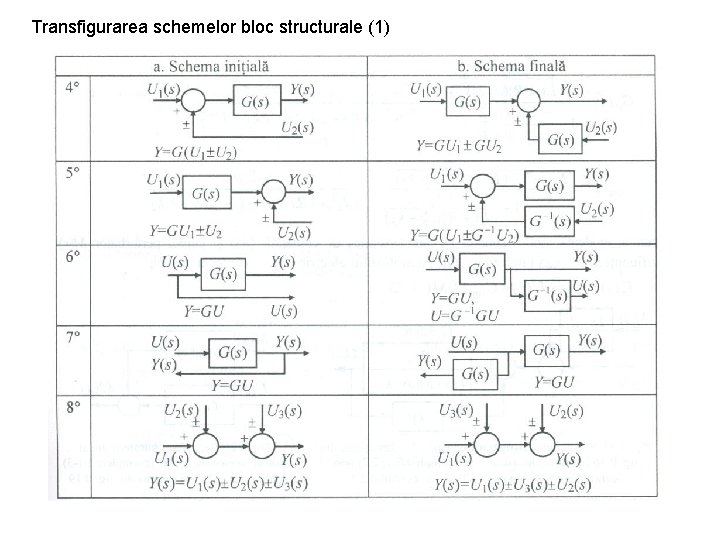
Transfigurarea schemelor bloc structurale (1)

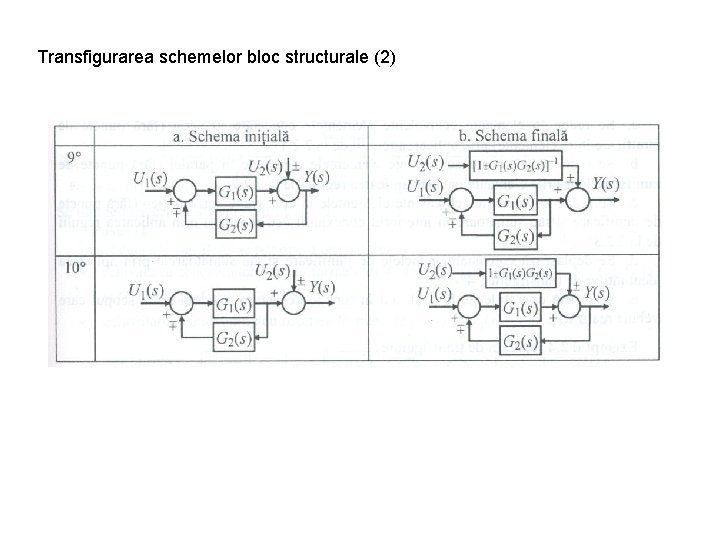
Transfigurarea schemelor bloc structurale (2)

Algoritm de transfigurare Se reduc la elemente echivalente elementele conectate in serie (fara puncte de ramificare intre elemente); Se reduc la elemente echivalente elementele conectate in paralel (fara puncte de ramificare la iesirile elementelor); Se reduc la elemente echivalente elementele in conexiune “cu reactie” (fara puncte de ramificare si/sau sumatoare in interiorul conexiunii “cu reactie”; Se deplaseaza convenabil punctele de ramificatie si/sau sumatoarele prin aplicarea identitatilor de transfigurare 4 -10; Se repeta operatiile de la pasii anteriori in functie de natura schemei si de scopul care trebuie realizat.