Describing Motion in One Dimension Motion The study

Describing Motion in One Dimension

Motion • The study of motion of bodies can be broadly separated into two separate sections, kinematics and dynamics. • Kinematics describes the motion of points and bodies (objects) without consideration of the cause of motion. • Dynamics is the study of motion in all its aspects, including the cause of the motion and the way in which moving bodies interact with each other when they collide.

Distance vs Displacement • Distance and displacement are two quantities that may seem to mean the same thing yet have distinctly different definitions and meanings. • Distance travelled, s, is how far a body travels during motion. – i. e. total distance than the body/object has travelled, or “how much ground an object has covered” during its motion – Measured in metres (m) • Displacement, s, is defined as the change in position of a body in a given direction. – i. e. how far the body/object has moved from its original position and the direction in which it has moved. – Displacement s = final position – initial position – Measured in metres (m)

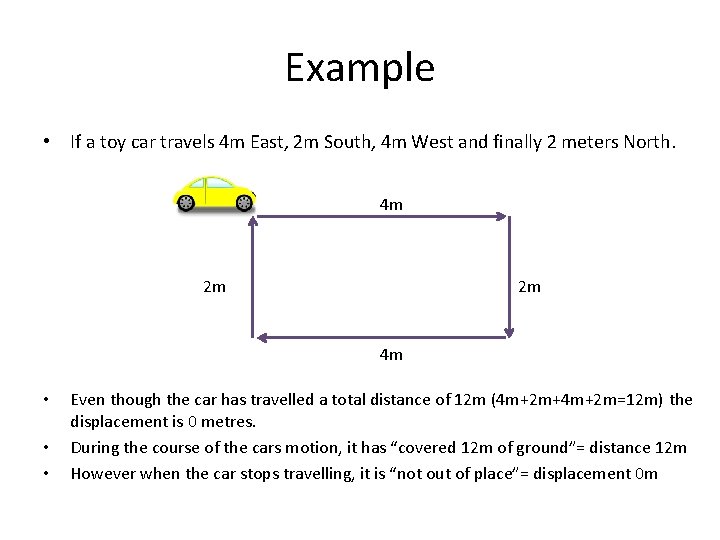
Example • If a toy car travels 4 m East, 2 m South, 4 m West and finally 2 meters North. 4 m 2 m 2 m 4 m • • • Even though the car has travelled a total distance of 12 m (4 m+2 m+4 m+2 m=12 m) the displacement is 0 metres. During the course of the cars motion, it has “covered 12 m of ground”= distance 12 m However when the car stops travelling, it is “not out of place”= displacement 0 m

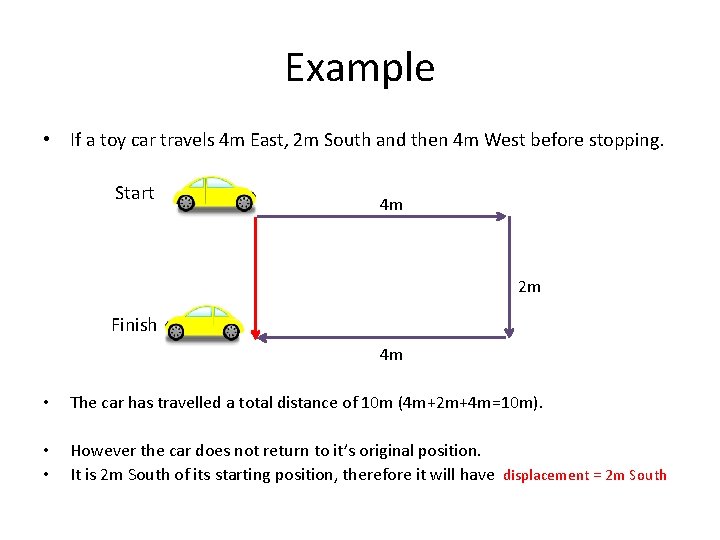
Example • If a toy car travels 4 m East, 2 m South and then 4 m West before stopping. Start 4 m 2 m Finish 4 m • The car has travelled a total distance of 10 m (4 m+2 m+4 m=10 m). • • However the car does not return to it’s original position. It is 2 m South of its starting position, therefore it will have displacement = 2 m South

Scalars and Vectors • Physical quantities requiring a number only to fully describe them are known as scalars. – Examples include distance, mass, time and speed • Physical quantities requiring a number (magnitude) and direction to fully describe them are known as vectors. – Examples include displacement, velocity, acceleration and force. • Note: Vector quantities are generally represented in bold italics.

Speed and Velocity • Speed and velocity are both quantities that give an indication of how fast an object moves or, more precisely, of how quickly the position of an object is changing. • Speed is defined in terms of the distance travelled over time – Therefore, like distance, speed is scalar quantity • Velocity is defined in terms of displacement over time – Therefore, like displacement, velocity is a vector quantity • The SI unit for speed and velocity is metres per second (ms-1) – Kilometres per hour (km h-1) is also commonly used

Instantaneous Speed and Velocity • Instantaneous speed and instantaneous velocity give a measure of how fast something is moving at a particular moment or instant in time. • E. g If a speedometer on a car shows 60 km h-1, it is indicating the instantaneous speed of the car.

Average Speed and Average Velocity • Average speed and average velocity both give an indication of how fast an object is moving over a time interval. • For example, the average speed of a car that takes 1 hour to travel 30 km from Craigmore to Adelaide is 30 km h-1 – However this does not mean that the car travelled the whole distance at this speed.

Example • Consider Jana, an athlete performing a training routine by running back and forth along a straight stretch of running track. She jogs 100 m north in a time of 20 s, then turns and walks 50 m south in a further 25 s before stopping. a. b. c. d. e. Calculate Jana’s average speed as she is jogging. What is her average velocity as she is jogging? What is her average speed for this 150 m exercise? Determine the average velocity for this activity. What is the magnitude of Jana’s average velocity in km h-1?

Example • Consider Jana, an athlete performing a training routine by running back and forth along a straight stretch of running track. She jogs 100 m north in a time of 20 s, then turns and walks 50 m south in a further 25 s before stopping. a. Calculate Jana’s average speed as she is jogging. b. What is her average velocity as she is jogging?

Example • Consider Jana, an athlete performing a training routine by running back and forth along a straight stretch of running track. She jogs 100 m north in a time of 20 s, then turns and walks 50 m south in a further 25 s before stopping. c. What is her average speed for this 150 m exercise? d. Determine the average velocity for this activity.

Example • Consider Jana, an athlete performing a training routine by running back and forth along a straight stretch of running track. She jogs 100 m north in a time of 20 s, then turns and walks 50 m south in a further 25 s before stopping. e. What is the magnitude of Jana’s average velocity in km h-1?

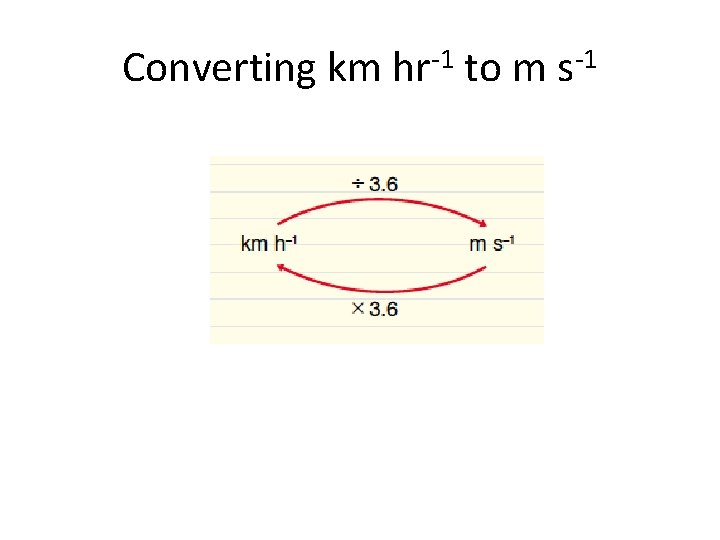
Converting km hr-1 to m s-1