Describing Data Summary Measures of Central Location Mean

Describing Data: Summary Measures of Central Location Mean, Median, Mode Measures of Variation Range, Variance and Standard Deviation Measures of Association Covariance and Correlation © 1999 Prentice-Hall, Inc. Chap. 3 - 1

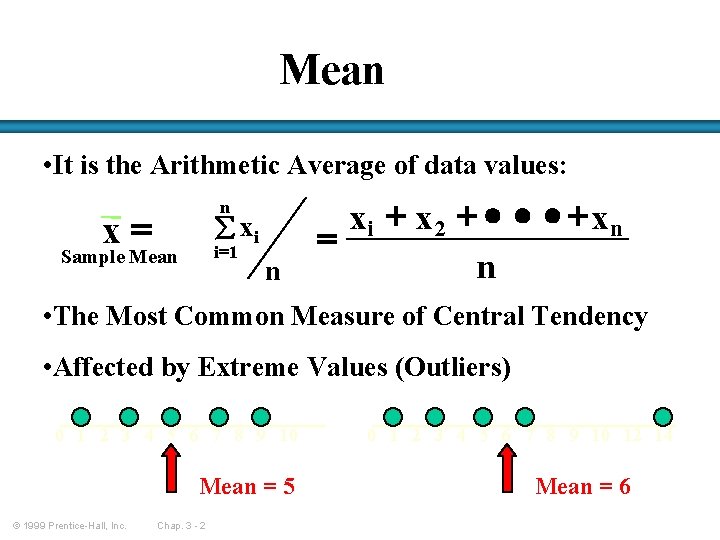
Mean • It is the Arithmetic Average of data values: n x= å xi i =1 Sample Mean n xi + x 2 + · · · + xn = n • The Most Common Measure of Central Tendency • Affected by Extreme Values (Outliers) 0 1 2 3 4 5 6 7 8 9 10 Mean = 5 © 1999 Prentice-Hall, Inc. Chap. 3 - 2 0 1 2 3 4 5 6 7 8 9 10 12 14 Mean = 6

Median • Important Measure of Central Tendency • In an ordered array, the median is the “middle” number. • If n is odd, the median is the middle number. • If n is even, the median is the average of the 2 middle numbers. • Not Affected by Extreme Values 0 1 2 3 4 5 6 7 8 9 10 Median = 5 © 1999 Prentice-Hall, Inc. Chap. 3 - 3 0 1 2 3 4 5 6 7 8 9 10 12 14 Median = 5

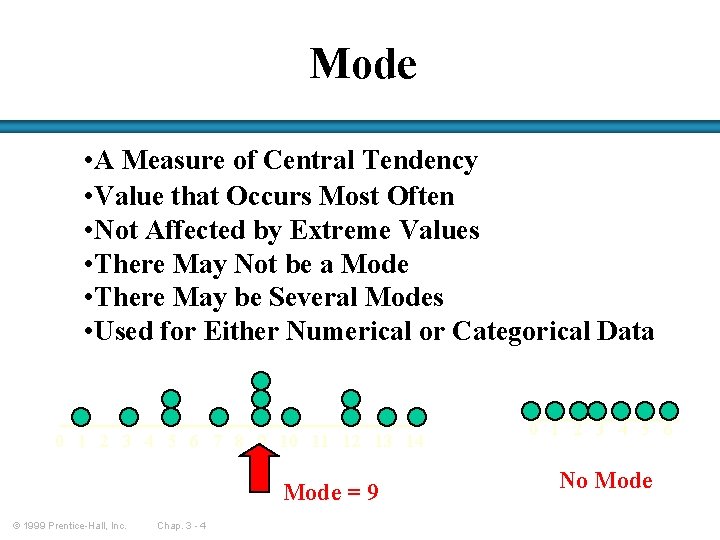
Mode • A Measure of Central Tendency • Value that Occurs Most Often • Not Affected by Extreme Values • There May Not be a Mode • There May be Several Modes • Used for Either Numerical or Categorical Data 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Mode = 9 © 1999 Prentice-Hall, Inc. Chap. 3 - 4 0 1 2 3 4 5 6 No Mode

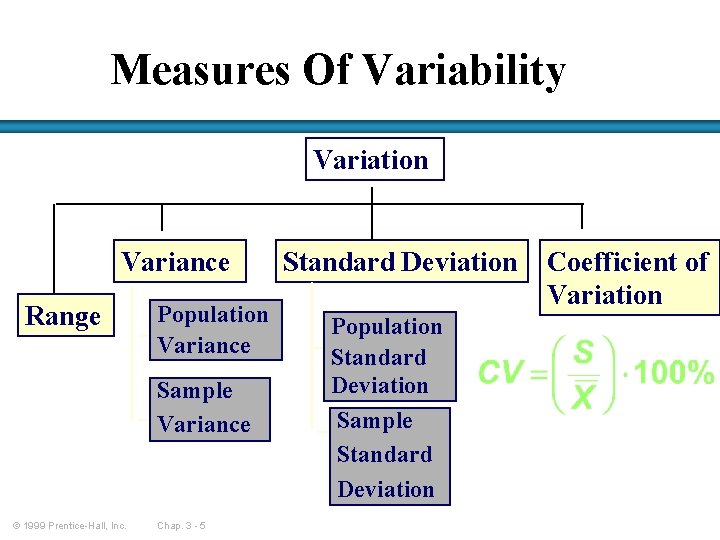
Measures Of Variability Variation Variance Range Population Variance Sample Variance © 1999 Prentice-Hall, Inc. Chap. 3 - 5 Standard Deviation Population Standard Deviation Sample Standard Deviation Coefficient of Variation

The Range • Measure of Variation • Difference Between Largest & Smallest Observations: Range = x Largest - x Smallest • Ignores How Data Are Distributed: Range = 12 - 7 = 5 7 8 © 1999 Prentice-Hall, Inc. 9 10 Chap. 3 - 6 11 12 7 8 9 10 11 12

Variance • Important Measure of Variation • Shows Variation About the Mean: 2 å (X-i m) 2 • For the Population: s = N • For the Sample: å (X i - X ) s = n -1 2 For the Population: use N in the denominator. © 1999 Prentice-Hall, Inc. Chap. 3 - 7 2 For the Sample : use n - 1 in the denominator.

Standard Deviation • Most Important Measure of Variation • Shows Variation About the Mean: 2 ( ) m • For the Population: s = å Xi N • For the Sample: s = For the Population: use N in the denominator. © 1999 Prentice-Hall, Inc. Chap. 3 - 8 å (X i - X n -1 ) 2 For the Sample : use n - 1 in the denominator.

Sample Standard Deviation ( - X) å X i s = n-1 Data: 10 2 12 n=8 For the Sample : use n - 1 in the denominator. 14 15 17 18 18 Mean =16 s= Sample Standard Deviation= 4. 2426 © 1999 Prentice-Hall, Inc. Chap. 3 - 9 24

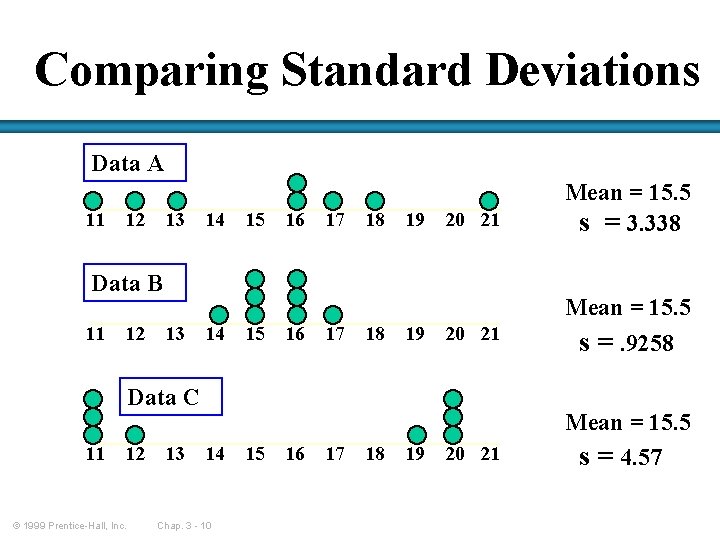
Comparing Standard Deviations Data A 11 12 13 14 15 16 17 18 19 20 21 Data B 11 12 13 14 15 16 17 18 19 20 21 Data C 11 12 © 1999 Prentice-Hall, Inc. 13 14 Chap. 3 - 10 15 16 17 18 19 20 21 Mean = 15. 5 s = 3. 338 Mean = 15. 5 s =. 9258 Mean = 15. 5 s = 4. 57

Coefficient of Variation • Measure of Relative Variation • Always a % • Shows Variation Relative to Mean • Used to Compare 2 or More Groups • Formula ( for Sample): © 1999 Prentice-Hall, Inc. Chap. 3 - 11

Comparing Coefficient of Variation Stock A: Average Price last year = $50 Standard Deviation = $5 Stock B: Average Price last year = $100 Standard Deviation = $5 Coefficient of Variation: Stock A: CV = 10% Stock B: CV = 5% © 1999 Prentice-Hall, Inc. Chap. 3 - 12

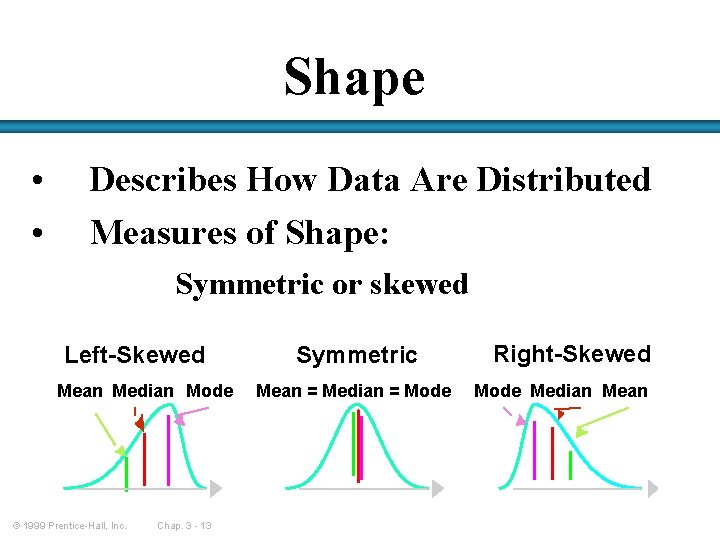
Shape • • Describes How Data Are Distributed Measures of Shape: Symmetric or skewed Left-Skewed Mean Median Mode © 1999 Prentice-Hall, Inc. Chap. 3 - 13 Symmetric Mean = Median = Mode Right-Skewed Mode Median Mean