DERS 2 SAYI DZENLER ERK u u u

DERS 2 SAYI DÜZENLERİ

İÇERİK u u u u u Ders 2, Slayt 2 Tarihçe Onluk sayı sistemi İkilik sayı sistemi Onluk/ikilik dönüşümleri İkilik sayı sisteminde toplama İkilik sayı sisteminde doğrudan çıkarma İkilik sayı sisteminde tümleyen aritmetiği ile çıkarma İkilik sayı sisteminde çarpma İkilik sayı sisteminde bölme Sekizli ve Onaltılı sayı sistemleri

TARİHÇE u u u Sayı ve sayma kavramının başlangıcı belirsiz Sümerler sayma işlemini kullanmışlar Günümüz rakam şekilleri MS 400 de Hindistan’da geliştirilmiş Bu rakamlar sonrasında müslümanlar tarafından da benimsenmiş Ebu Abdullah bin Musa El Harzemi (MS 780850 ) ‘Cebir ve denklem hesabı hakkında özetlenmiş kitap’ adlı kitabıyla: w w Ders 2, Slayt 3 Sıfır sayısını Onluk sayı sistemini tanıttı

Onluk Sayı Düzeni Onluk sayı düzeninde on değişik sembol rakamsal büyüklükleri tanımlamak için kullanılır. Bunlar: 0 1 2 3 4 5 6 7 8 9 Ders 2, Slayt 4

Onluk Sayı Düzeni Onluk sayı düzeninde, sayının en sağdaki rakamı en düşük, en soldaki rakamı da en yüksek değeri ifade edecek şekilde düzenlenmiştir. Burada sayının her bir basamağı ile ifade edilen büyüklük aşağıdaki yaklaşımdaki gibi 10 değerinin üstsel katları olarak belirlenir. . 10^4 10^3 5. Ders 2, Slayt 5 4. 10^2 10^1 10^0 3. 2. 1. basamak

Onluk Sayı Düzeni Buna göre her bir rakamın sayı içerisinde ifade ettiği değer: ilgili rakam ile o rakamın belirlediği basamak değerinin büyüklüğünün çarpımı olarak belirlenir. Buna göre bir sayı ile ifade edilen değer: ilgili sayı içerisindeki her bir rakamın ifade ettiği değerlerin toplamı olarak belirlenir. Ders 2, Slayt 6

Onluk Sayı Düzeni ÖRNEK: 3954 sayısı ile ifade edilen değer 3 x 1000 + 9 x 100 + 5 x 10 + 4 x 1 olarak hesaplanır. 10 tabanında tanımlanmış sayısal değerler yaygın olarak kullanıldıkları için tabanın 10 olduğunu belirlemede özel bir notasyon kullanılmamaktadır. Ders 2, Slayt 7

Diğer Sayı Düzenleri Kullanılan başka sayı düzenleri de vardır. Bunlarda da onluk sayı düzenindeki gibi basamak ağırlıklarının soldan sağa doğru azalması ve basamak değerlerinin ilgili tabanın basamak sırasının üstsel kuvveti olarak düzenlenmesi prensibi kullanılır. Ders 2, Slayt 8

İkili Sayı Düzeni İkili sayı düzeninde kullanılan rakamlar: 0 ve 1 olarak tanımlıdır. İkili sayı sistemi bilgisayar uygulamalarında iki farklı lojik seviye kullanım ihtiyacını karşıladığı için yaygın olarak kullanılır. Ders 2, Slayt 9

İkili Sayı Düzeni İkili sayı düzeninde her bir basamağa BİT adı verilmektedir. Dolayısıyla en sağdaki basamağa en düşük anlamlı bit (DAB-LSB) en soldaki basamağa en yüksek anlamlı bit (YAB-MSB) adı verilir. İkilik (binary) sayılar: w 0 b 1111 w b’ 1111’ (PIC işlemci notasyonu) w % 1111 w Ders 2, Slayt 10 11112 farklı biçimlerinde gösterilirler

İkilik – Onluk Dönüşümü Aynı onluk düzende olduğu gibi her bir basamağın ifade ettiği değer ile ilgili basamağın sayısal değerleri çarpılıp toplanarak elde edilirler. Örnek: İkilik düzende 10111 sayısının onluk düzende karşılığını hesaplayalım. 1 x 24 + 0 x 23 + 1 x 22 + 1 x 21 + 1 x 20 = 23 olur Ders 2, Slayt 11

Onluk-İkilik Dönüşümü ARAMA YÖNTEMİ Sayı içerisinde ikinin kuvvetini armaya dayanır. 23 sayısı için; 23 – 32 = -11 YOK => 0 23 – 16 = 7 VAR => 1 7 – 8 = -1 YOK => 0 7 – 4 = 3 VAR => 1 3 – 2 = 1 VAR => 1 1 – 1 = 0 VAR => 1 010111 veya 10111 ikilik düzendeki karşılığı elde edilir. Ders 2, Slayt 12

Onluk-İkilik Dönüşümü BÖLME YÖNTEMİ Sayı Sürekli 2’ye bölünür ve kalanın 1 yada 0 oluşuna bakılarak basamaklar belirlenir KALAN 23/2 = 11 1 VAR => 1 11/2 = 5 1 VAR => 1 5/2 = 2 1 VAR => 1 2/2 = 1 0 VAR => 0 1/2 = 0 1 VAR => 1 10111 ikilik düzendeki karşılığı Ders 2, Slayt 13

İkilik Tabanda İşlemler: TOPLAMA Aynı onluk tabanda uygulanan kurallar uygulanır. Tek fark her basamaktaki toplama sırasında elde değerinin 10 yerine 2 sayısına ulaşmasıdır. 0+0 = 0 0+1 = 1 1+0 = 1 1+1 = 0 ve de elde 1 Ders 2, Slayt 14

İkilik Tabanda İşlemler: TOPLAMA Örnek: + 11001 101110 Ders 2, Slayt 15

İkilik Tabanda İşlemler: ÇIKARMA Aynı onluk tabanda uygulanan kurallar uygulanır. Farklı olarak tümleyen aritmetiğine göre yapılan çıkarma işlemi de tanımlıdır. Ders 2, Slayt 16

İkilik Tabanda İşlemler: ÇIKARMA DOĞRUDAN ÇIKARMA: 0 -0 = 0 1 -0 = 1 1 -1 = 0 0 -1 = 1 ve de borç 1 Ders 2, Slayt 17

İkilik Tabanda İşlemler: ÇIKARMA Örnek: % 11001 % 10101 % 00100 Ders 2, Slayt 18

İkilik Tabanda İşlemler: ÇIKARMA TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA: Çıkarma işleminde kalanın sıfır veya sıfırdan büyük olması durumunda doğrudan çıkarma basamakları uygulanırken aksi durumda problem çıkmaktadır. Bu problemi daha pratik olarak çözmek için toplama işlemi şeklinde tanımlı çıkarma işlemi yaklaşımı mevcuttur. Buradaki yaklaşım belli sayıda basamak ile ifade edilen bir sayının alabileceği en büyük değere 1 sayısının ilave edilmesi durumunda sayının 0 değerini (ama elde 1 ile) alması özelliğini kullanmaktır. Ders 2, Slayt 19

TÜMLEYEN ARİTMETİĞİ Yani, bir a sayısına 1 eklendiğinde sonuç 0 oluyorsa a sayısının değeri -1 miş veya bir a sayısına 2 eklendiğinde sonuç 0 oluyorsa a sayısının değeri -2 miş veya bir a sayısına 3 eklendiğinde sonuç 0 oluyorsa a sayısının değeri -3 müş gibi bir yaklaşım kullanılır. Ders 2, Slayt 20

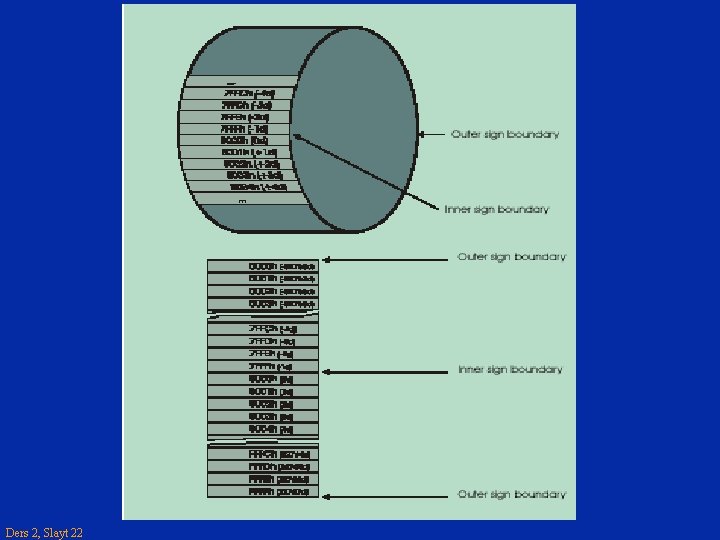
TÜMLEYEN ARİTMETİĞİ O zaman: u 0 sayısından sonra + sayılar sıralanır u 0 sayısından önce – sayılar sıralanır u. Tüm sayılar bir silindir üzerinde sıralı olarak düşünülürse (otomobil km sayacı gibi) en büyük sayıdan sonra tekrar en küçük sayıya dönülür u. Maksimum sayıda + ve – sayıyı ifade etmek için silindiri ortadan ikiye bölelim Sonuç: u(1 ) - (2 N-1– 1) arası sayılar pozitif (2 N-1– 1 adet) u(2 N-1) - (2 N ) arası sayılar negatif (2 N-1 adet) Ders 2, Slayt 21

Ders 2, Slayt 22

TÜMLEYEN ARİTMETİĞİ Sonuç DEVAM: u. Tüm pozitif sayılar işaretsiz gösterimleri ile aynıdır u. Tüm pozitif sayılar için MSB 0 olur u 0 hariç iken en büyük pozitif sayı 2 N-1 -1 olur (2 N/2 -1) u. Tüm negatif sayılar için MSB 1 olur u. En küçük negatif sayı -2 N-1 (2 N/2 -1+1) u. Dolayısıyla MSB işaret biti olarak anılır u. Küçük + sayılarda MSB sağında 0 çoktur u. Küçük – sayılarda MSB sağında 1 azdır u. Büyük + sayılarda MSB sağında 0 azdır u. Büyük – sayılarda MSB sağında 1 çoktur Ders 2, Slayt 23

TÜMLEYEN ARİTMETİĞİ Sayının işaretini değiştirmek için u. Sayının tümleyeni hesaplanır (1’e tümleme) u. Sayının tümleyenine 1 sayısı eklenir (2’ye tüm) Ders 2, Slayt 24

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA Örnek: % 11111 + % 00001 % 1 000001 ve 11111 sayılarına birbirlerinin 2’ye (tabana) göre tümleyeni adı verilmektedir. Benzer şekilde 00010 ve 11110 sayıları da aynı özelliği gösterirler. Ders 2, Slayt 25

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA Bu yaklaşım göz önünde bulundurularak tümleyen aritmetiği ile çıkarma işleminde, çıkarılacak sayının çıkarılması yerine bu sayının 2’ye (yani taban değerine) tümleyeni kendisinden çıkarılacak sayıya eklenir. Dolayısıyla çıkarma işlemi toplama işlemi şeklinde tanımlanmış olur. Ders 2, Slayt 26

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA Örnek: Onluk tabanda 0008 sayısından 0003 sayısını çıkaralım. 0003 => 9997 sayının tabana (10) göre tümleyeni Tabana göre tümleyen ile sayının toplamı aynı sayıda basamak üzerinden 0 sonucunu verir. 0003 + 9997 = 1 0000 olur (4 basamak için doğru) O zaman -0003 -9997 = 0 => -0003 = 9997 olur. 0008 – 0003 = 0008 + 9997 = 1 0005 Bu ne demek? Ders 2, Slayt 27

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA Yani sonuç 0005 olarak bulunur. Ancak bu değerin düzenlenmesi gerekebilir. Bu işlem sonucundaki elde bitine İŞARET BİTİ adı verilir ve sonuç bu bite göre düzenlenir. Eğer işaret biti 1 ise sonuç + dır ve aynı bırakılır Eğer işaret biti 0 ise sonuç – dir ve düzenlenir. NEDEN? Ders 2, Slayt 28

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA 4 bit ile 0 -15 arası tamsayıları ifade etmek mümkün olabilir: 0 0000 1 0001 1111 15 2 0010 1110 14 3 0011 1101 13 4 0100 12 5 0101 1011 11 6 0110 10 7 0111 1001 9 1000 8 Ders 2, Slayt 29

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA Yada alternatif olarak – 8 ile 7 arası tamsayılar da ifade edilebilirler: +0 0000 +1 0001 1111 -1 +2 0010 1110 -2 +3 0011 1101 -3 +4 0100 1100 -4 +5 0101 1011 -5 +6 0110 1010 -6 +7 0111 1001 -7 1000 -8 Ders 2, Slayt 30

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA Burada 10 tabanında gösterildiği gibi 2 tabanına göre tümleme kabulü yapılmaktadır. +0 0000 +1 0001 + 1111 -1 = 1 0000 +2 0010 + 1110 -2 = 1 0000 +3 0011 + 1101 -3 = 1 0000 +4 0100 + 1100 -4 = 1 0000 +5 0101 + 1011 -5 = 1 0000 +6 0110 + 1010 -6 = 1 0000 +7 0111 + 1001 -7 = 1 0000 1000 -8 Ders 2, Slayt 31

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA İkilik düzende bir sayının tabana tümleyeni için 1) Sayının 1’e tümleyeni hesaplanır 2) Elde edilen sayıya 1 değeri eklenir 3) 4) 5) Ders 2, Slayt 32 ÖRNEK: verilen sayı 1’e tümleyeni 2’ye tümleyeni % 10111 % 01000 % 01001

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA ÖRNEK: % - % % % Yani % + % %1 11001 101010 01011 11001 01011 00100 elde işaretsonuç Ders 2, Slayt 33 25 21 21’in 1’e tümleyeni 21’in 2’ye tüm. 25 21’in 2’ye tüm.

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA ÖRNEK: % - % % % Yani % + % %0 10101 11001 00110 00111 10101 00111 11100 elde işaretsonuç Ders 2, Slayt 34 21 25 25’in 1’e tümleyeni 25’in 2’ye tüm. 21 25’in 2’ye tüm.

TÜMLEYEN ARİTMETİĞİ İLE ÇIKARMA ÖRNEK devam: İşaret biti 1 yani negatif olduğu için sonucun düzenlenmesi gerekir. Bunun için de sonucun 2’ye tümleyeninin hesaplanması gerekir. % 11100 % 00011 % 00100 => 4 yani -4 sayısı elde edilir. Ders 2, Slayt 35

İkilik Tabanda İşlemler: ÇARPMA Onluk tabanda tanımlanmış yöntemlerin benzerleri geçerlidir. Bunlar: 0 x 0=0 0 x 1=0 1 x 0=0 1 x 1=1 Taban ile çarpma (2 ile) bir bit sola kayma olarak tanımlanır Ders 2, Slayt 36

İkilik Tabanda İşlemler: ÇARPMA ÖRNEK: %101 ve %10 sayılarının çarpımını hesaplayalım. 101 x 10 000 + 1010 Ders 2, Slayt 37

İkilik Tabanda İşlemler: BÖLME Onluk tabanda tanımlanmış yöntemlerin benzerleri geçerlidir. Taban ile bölme (2 ile) bir bit sağa kayma olarak tanımlanır. ÖRNEK: 1010 : 11 veya 10 tabanında 10 : 3 - 0000 011 9 3 1010 1 - 110 100 - 11 1 Ders 2, Slayt 38

Sekizli Sayı Düzeni Sekizli sayı düzeninde kullanılan rakamlar: 0 1 2 3 4 5 6 7 olarak tanımlıdır. Sekizli düzende verilen sayılar: w 0 o 7777 w& w Ders 2, Slayt 39 77778 biçimlerinde gösterilirler

Sekizli Sayı Düzeni uİkili sayı sisteminde ifade edilen sayıların büyük olması durumunda gösterimleri çok uzun olabilmektedir. u. Bu problemi gidermek üzere kullanılan yaklaşımlardan biri sekizli sayı sistemini kullanmaktır. u. Bunun avantajı ikili dönüşümlerin pratik oluşudur. Ders 2, Slayt 40 sistemle

İkili/Sekizli Taban Dönüşümleri İkili sayı düzeninde verilen bir sayının bitleri 3 lü gruplar halinde düzenlenir. Bu 3 lü grupların her birinin ifade ettiği sayılar sağdan sola doğru yazıldıklarında ikili sayı düzeninden sekizli sayı düzenine dönüşüm gerçeklenir. Sekizliden ikili sayı düzenine dönüşüm de benzer adımlar ters sırada yapılarak elde edilir. Ders 2, Slayt 41

İkili/Sekizli Taban Dönüşümleri ÖRNEK: % 01011100101000 sayısını sekizli sayı düzeninde gösterelim. 010 1 1 1 000 => 4096 + 1024 + 512 + 256 + 32 + 8 = 5928 001 011 100 101 000 Ders 2, Slayt 42

Onaltılı (Hexadecimal) Sayı Düzeni Onaltılı sayı düzeninde kullanılan rakamlar: 0 1 2 3 4 5 6 7 8 9 A B C D E F olarak tanımlıdır. Burada: A=10 B=11 C=12 D=13 E=14 F=15 değerlerini ifade ederler. Onaltılı düzende verilen sayılar: w 0 x FFFF (PIC işlemci notasyonu) w h’FFFF’ (PIC işlemci notasyonu) w w Ders 2, Slayt 43 $ FFFF 16 veya FFFFh biçimlerinde gösterilirler

İkili/Onaltılı Taban Dönüşümleri İkili sayı düzeninde verilen bir sayının bitleri 4 lü gruplar halinde düzenlenir. Bu 4 lü grupların her birinin ifade ettiği sayılar sağdan sola doğru yazıldıklarında ikili sayı düzeninden onaltılı sayı düzenine dönüşüm gerçeklenir. Onaltılıdan ikili sayı düzenine dönüşüm de benzer adımlar ters sırada yapılarak elde edilir. Ders 2, Slayt 44

DERS 2 SAYI DÜZENLERİ -SON – -Kaynaklar: -1) An Introduction to Digital Signal Processors, Bruno Paillard -2) Mikroişlemciler Mikrobilgisayarlar, Eşref Adalı, ISBN 975 -511 -175 -1