Deriving the equations of motion a graphical explanation

Deriving the equations of motion a graphical explanation of where they come from. By J. Jaffrey at Long Bay College, NZ

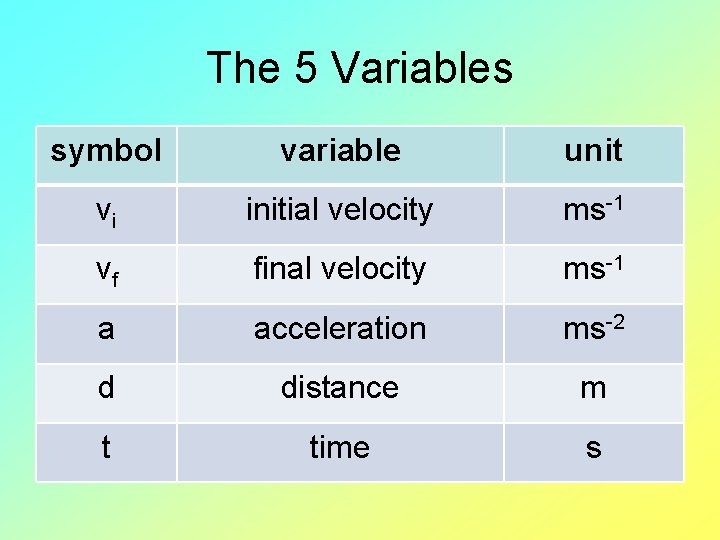
The 5 Variables symbol variable unit vi initial velocity ms-1 vf final velocity ms-1 a acceleration ms-2 d distance m t time s

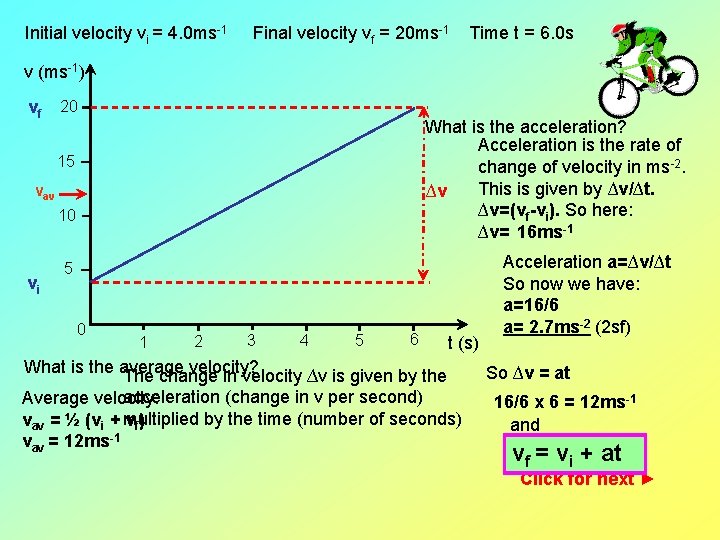
Imagine you are cycling and reach a hill. You pedal and accelerate steadily down the hill. You start at 4. 0 ms-1 and after 6. 0 s end up at 20 ms-1. Initial velocity vi = 4. 0 ms-1 Final velocity vf = 20 ms-1 Time t = 6. 0 s We can plot this motion on a graph with velocity on the vertical axis and time on the horizontal axis. Click for next ►

Initial velocity vi = 4. 0 ms-1 Final velocity vf = 20 ms-1 Time t = 6. 0 s v (ms-1) vf 20 What is the acceleration? Acceleration is the rate of change of velocity in ms-2. This is given by ∆v/∆t. ∆v ∆v=(vf-vi). So here: ∆v= 16 ms-1 15 vav 10 vi 5 0 1 2 3 4 5 6 t (s) What is the average velocity? The change in velocity ∆v is given by the acceleration (change in v per second) Average velocity: by the time (number of seconds) vav = ½ (vi + multiplied vf) vav = 12 ms-1 Acceleration a=∆v/∆t So now we have: a=16/6 a= 2. 7 ms-2 (2 sf) So ∆v = at 16/6 x 6 = 12 ms-1 and vf = vi + at Click for next ►

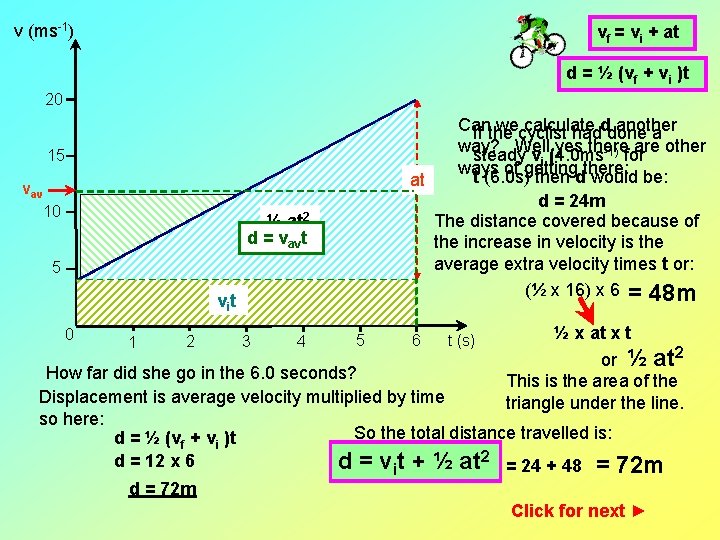
v (ms-1) vf = vi + at d = ½ (vf + vi )t 20 15 at vav 10 d = 24 m The distance covered because of the increase in velocity is the average extra velocity times t or: (½ x 16) x 6 = 48 m ½ at 2 d = vavt 5 vit 0 1 2 3 4 Can wecyclist calculate another If the hadddone a way? Well yes there are other -1) for steady vi (4. 0 ms ways of getting t (6. 0 s) then dthere: would be: 5 6 t (s) ½ x at x t or ½ at 2 This is the area of the triangle under the line. How far did she go in the 6. 0 seconds? Displacement is average velocity multiplied by time so here: So the total distance travelled is: d = ½ (vf + vi )t d = 12 x 6 d = vit + ½ at 22 = 24 + 48 = 72 m d = 72 m i Click for next ►

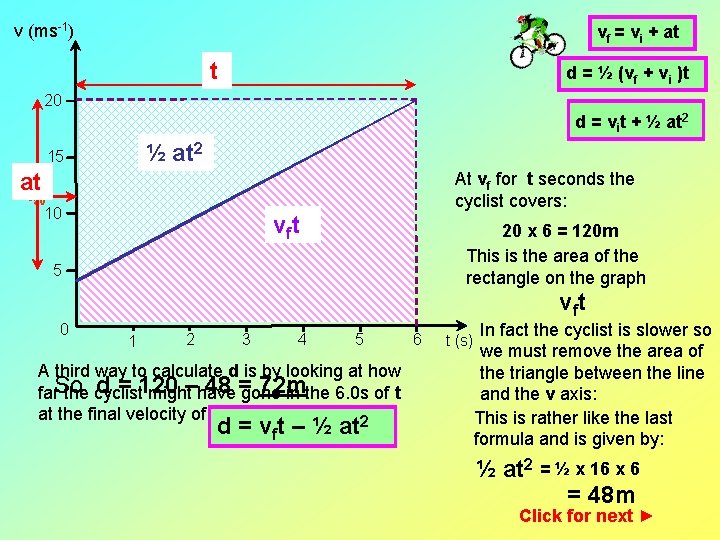
v (ms-1) vf = vi + at t d = ½ (vf + vi )t 20 d = vit + ½ at 2 15 at v At vf for t seconds the cyclist covers: av 10 v ft 20 x 6 = 120 m This is the area of the rectangle on the graph 5 v ft 0 1 2 3 4 5 A third way to calculate d is by looking at how d = 120 48 =gone 72 m far. So the cyclist might–have in the 6. 0 s of t at the final velocity of 20 ms-1 vf 2 d = vft – ½ at 6 t (s) In fact the cyclist is slower so we must remove the area of the triangle between the line and the v axis: This is rather like the last formula and is given by: ½ at 2 = ½ x 16 x 6 = 48 m Click for next ►

Initial velocity vi = 4. 0 ms-1 Final velocity vf = 20 ms-1 Time t = 6. 0 s d = 72 m The last equation cannot be shown easily from a graph. However it can be derived using algebra. vf = vi + at square both sides vf 2 = (vi + at)2 expand vf 2 = vi 2 + 2 viat +a 2 t 2 extract 2 a vf 2 = vi 2 + 2 a ( vit + ½ at 2 ) But this term in brackets is simply d so simplifying we get our final equation of motion: vf 2 = vi 2 + 2 ad (ms-1)2 All three terms give: ms-2 m vf = =v vi + + at at v f i d = ½ (vf + vi )t d = vit + ½ at 2 d = vft – ½ at 2 vf 2 = vi 2 + 2 ad m 2 s-2 We can check the units both sides are the same. Click for next ►

The Equations of Motion vf = vi + at d = ½ (vf + vi )t d = vit + ½ at 2 d = vft – ½ at 2 vf 2 = vi 2 + 2 ad Click to finish