DERIVING LINEAR REGRESSION COEFFICIENTS Y X This sequence



















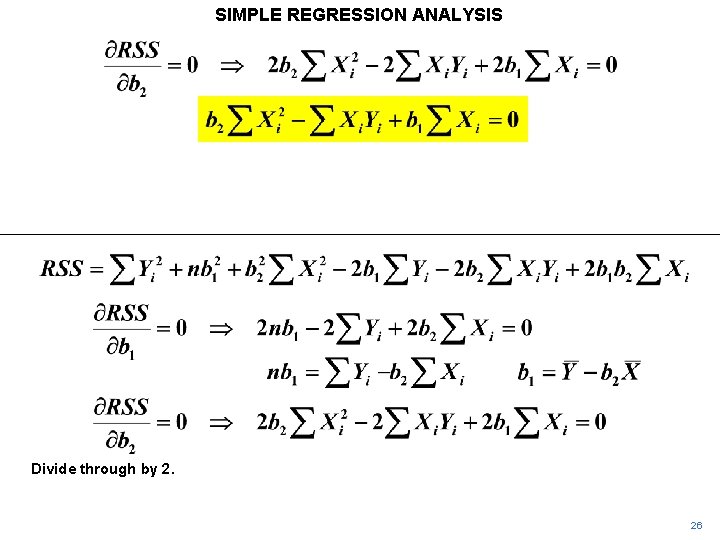















- Slides: 41

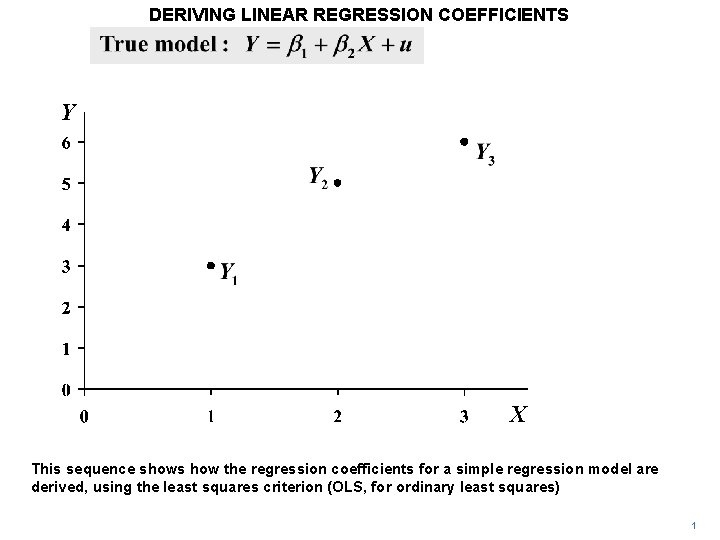
DERIVING LINEAR REGRESSION COEFFICIENTS Y X This sequence shows how the regression coefficients for a simple regression model are derived, using the least squares criterion (OLS, for ordinary least squares) 1

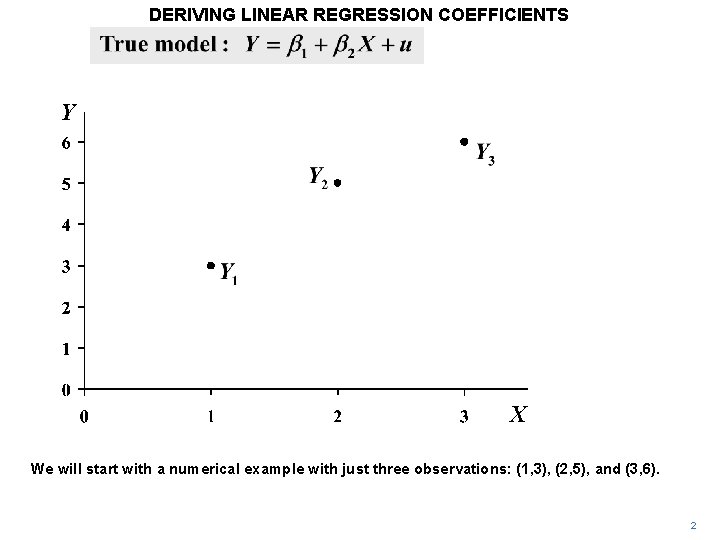
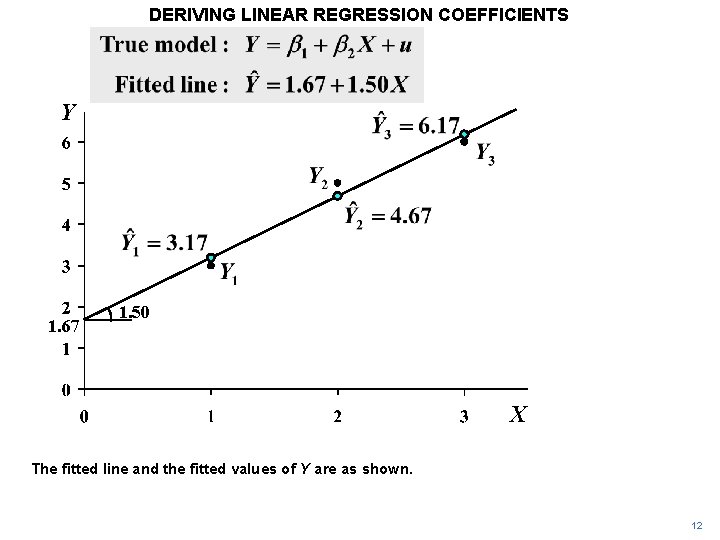
DERIVING LINEAR REGRESSION COEFFICIENTS Y X We will start with a numerical example with just three observations: (1, 3), (2, 5), and (3, 6). 2

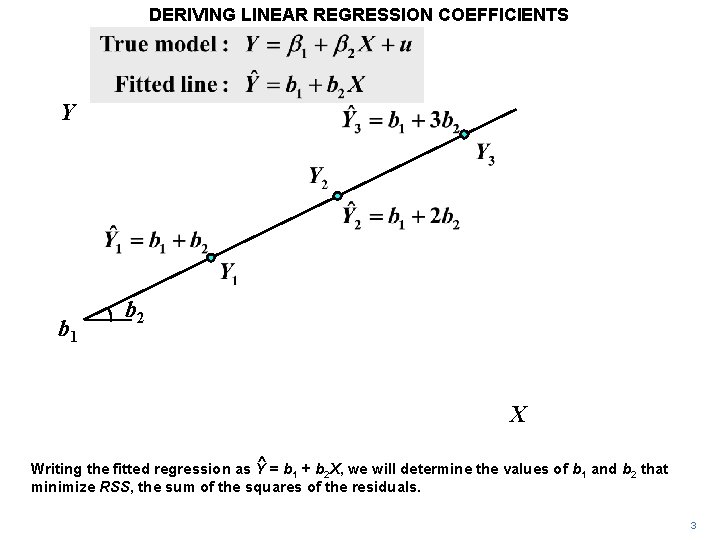
DERIVING LINEAR REGRESSION COEFFICIENTS Y b 1 b 2 X ^ = b + b X, we will determine the values of b and b that Writing the fitted regression as Y 1 2 minimize RSS, the sum of the squares of the residuals. 3

DERIVING LINEAR REGRESSION COEFFICIENTS Y b 1 b 2 X Given our choice of b 1 and b 2, the residuals are as shown. 4

SIMPLE REGRESSION ANALYSIS The sum of the squares of the residuals is thus as shown above. 5

SIMPLE REGRESSION ANALYSIS The quadratics have been expanded. 6

SIMPLE REGRESSION ANALYSIS Like terms have been added together. 7

SIMPLE REGRESSION ANALYSIS For a minimum, the partial derivatives of RSS with respect to b 1 and b 2 should be zero. (We should also check a second-order condition. ) 8

SIMPLE REGRESSION ANALYSIS The first-order conditions give us two equations in two unknowns. 9

SIMPLE REGRESSION ANALYSIS Solving them, we find that RSS is minimized when b 1 and b 2 are equal to 1. 67 and 1. 50, respectively. 10

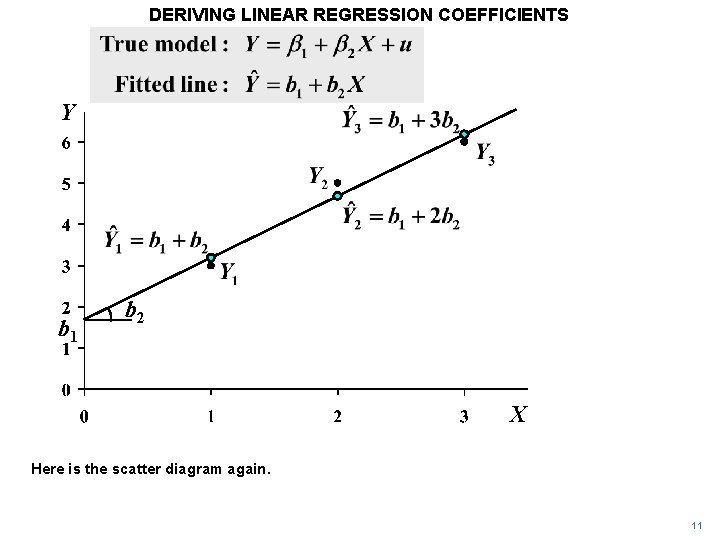
DERIVING LINEAR REGRESSION COEFFICIENTS Y b 1 b 2 X Here is the scatter diagram again. 11

DERIVING LINEAR REGRESSION COEFFICIENTS Y 1. 67 1. 50 X The fitted line and the fitted values of Y are as shown. 12

DERIVING LINEAR REGRESSION COEFFICIENTS Y X 1 Xn X Now we will do the same thing for the general case with n observations. 13

DERIVING LINEAR REGRESSION COEFFICIENTS Y b 1 b 2 X 1 Xn X Given our choice of b 1 and b 2, we will obtain a fitted line as shown. 14

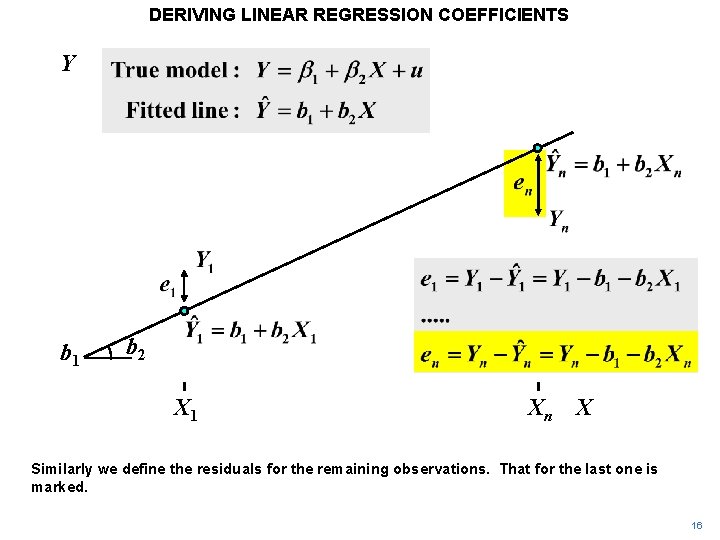
DERIVING LINEAR REGRESSION COEFFICIENTS Y b 1 b 2 X 1 Xn X The residual for the first observation is defined. 15

DERIVING LINEAR REGRESSION COEFFICIENTS Y b 1 b 2 X 1 Xn X Similarly we define the residuals for the remaining observations. That for the last one is marked. 16

DERIVING LINEAR REGRESSION COEFFICIENTS RSS, the sum of the squares of the residuals, is defined for the general case. The data for the numerical example are shown for comparison. . 17

DERIVING LINEAR REGRESSION COEFFICIENTS The quadratics are expanded. 18

DERIVING LINEAR REGRESSION COEFFICIENTS Like terms are added together. 19

DERIVING LINEAR REGRESSION COEFFICIENTS Note that in this equation the observations on X and Y are just data that determine the coefficients in the expression for RSS. 20

DERIVING LINEAR REGRESSION COEFFICIENTS The choice variables in the expression are b 1 and b 2. This may seem a bit strange because in elementary calculus courses b 1 and b 2 are usually constants and X and Y are variables. 21

DERIVING LINEAR REGRESSION COEFFICIENTS However, if you have any doubts, compare what we are doing in the general case with what we did in the numerical example. 22

DERIVING LINEAR REGRESSION COEFFICIENTS The first derivative with respect to b 1. 23

DERIVING LINEAR REGRESSION COEFFICIENTS With some simple manipulation we obtain a tidy expression for b 1. 24

DERIVING LINEAR REGRESSION COEFFICIENTS The first derivative with respect to b 2. 25
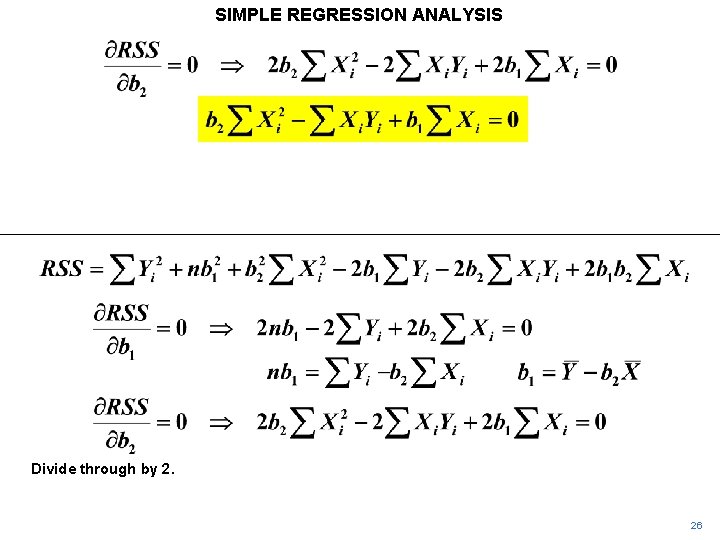
SIMPLE REGRESSION ANALYSIS Divide through by 2. 26

SIMPLE REGRESSION ANALYSIS We now substitute for b 1 using the expression obtained for it and we thus obtain an equation that contains b 2 only. 27

SIMPLE REGRESSION ANALYSIS The definition of the sample mean has been used. 28

SIMPLE REGRESSION ANALYSIS The last two terms have been disentangled. 29

SIMPLE REGRESSION ANALYSIS Terms not involving b 2 have been transferred to the right side. 30

SIMPLE REGRESSION ANALYSIS To create space, the equation is shifted to the top of the slide. 31

SIMPLE REGRESSION ANALYSIS Hence we obtain an expression for b 2. 32

SIMPLE REGRESSION ANALYSIS In practice, we shall use an alternative expression. We will demonstrate that it is equivalent. 33

SIMPLE REGRESSION ANALYSIS Expanding the numerator, we obtain the terms shown. 34

SIMPLE REGRESSION ANALYSIS In the second term the mean value of Y is a common factor. In the third, the mean value of X is a common factor. The last term is the same for all i. 35

SIMPLE REGRESSION ANALYSIS We use the definitions of the sample means to simplify the expression. 36

SIMPLE REGRESSION ANALYSIS Hence we have shown that the numerators of the two expressions are the same. 37

SIMPLE REGRESSION ANALYSIS The denominator is mathematically a special case of the numerator, replacing Y by X. Hence the expressions are quivalent. 38

DERIVING LINEAR REGRESSION COEFFICIENTS Y b 1 b 2 X 1 Xn X The scatter diagram is shown again. We will summarize what we have done. We hypothesized that the true model is as shown, we obtained some data, and we fitted a line. 39

DERIVING LINEAR REGRESSION COEFFICIENTS Y b 1 b 2 X 1 Xn X We chose the parameters of the fitted line so as to minimize the sum of the squares of the residuals. As a result, we derived the expressions for b 1 and b 2. 40

Copyright Christopher Dougherty 1999– 2006. This slideshow may be freely copied for personal use. 17. 06