DERIVING GAS LAWS The relationship between temperature and

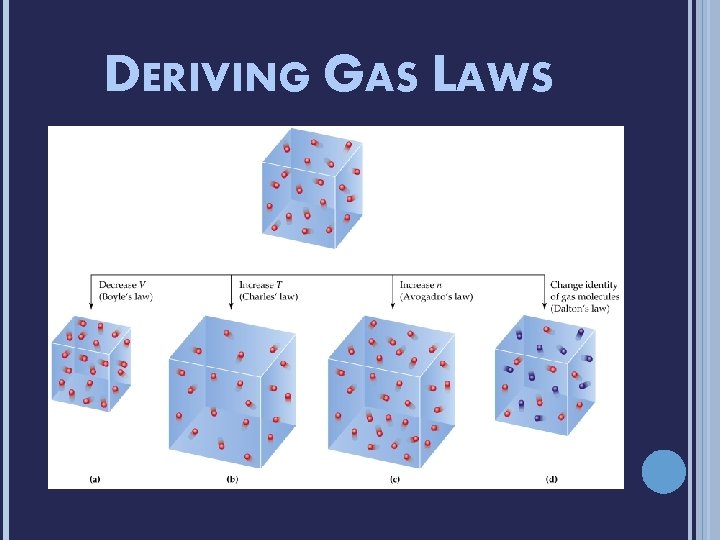
DERIVING GAS LAWS

The relationship between temperature and volume

HOW VOLUME VARIES WITH TEMPERATURE If we place a balloon in liquid nitrogen it shrinks: So, gases shrink if cooled. Conversely, if we heat a gas it expands (as in a hot air balloon). Let’s take a closer look at temperature before we try to find the exact relationship of V vs. T. Link to liquid nitrogen video

Molecular Level Picture of Charles’ Law • Constant Pressure (allow piston to move freely) • Constant moles of gas (sealed system) • As Temperature ↑, molecules ↑ speed → molecules strike piston more frequently and with more force pushing piston to larger volume in order to maintain constant pressure (constant total force of collisions) Link to Charles’ Law Link to Gas Laws simulation Link to phet

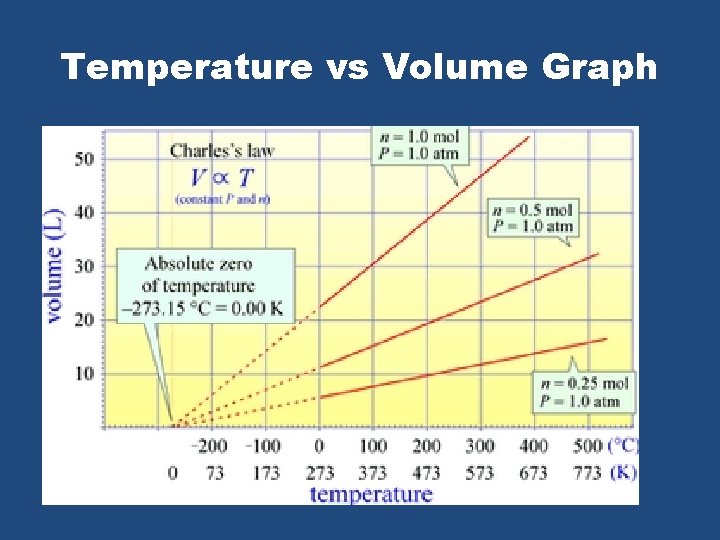
Temperature vs Volume Graph

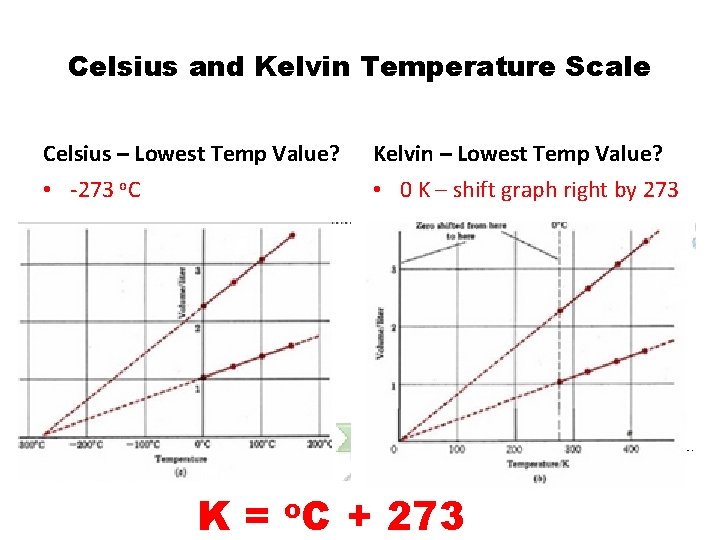
Celsius and Kelvin Temperature Scale Celsius – Lowest Temp Value? Kelvin – Lowest Temp Value? • -273 o. C • 0 K – shift graph right by 273 K = o. C + 273

TEMPERATURE IS EXPRESSED IN K FOR ALL GAS LAWS Kelvin Temp is directly proportional to average Kinetic Energy Lowest Value of Kelvin is zero (absolute zero). At 0 K all atomic motion ceases. Kelvin Temperature is never negative. Negative Temp values create physically impossible calculations (eg negative volumes gases occupying less than no space)

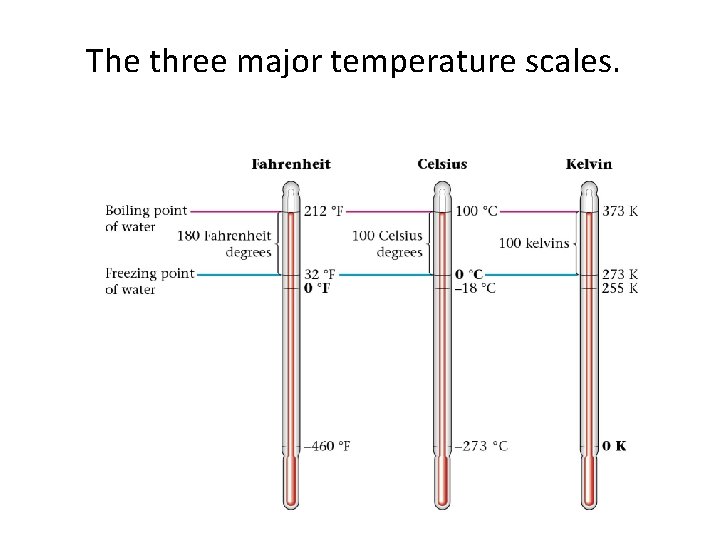
The three major temperature scales.

Comparing Celsius and Kelvin Temperature • Is 20 K twice as hot as 10 K? • Yes. Kelvin scale lowest value starts at 0 K and goes up. • Is 20 o. C is twice as hot as 10 o. C? • No. The celsius temperature scale starts at • -273, not zero.

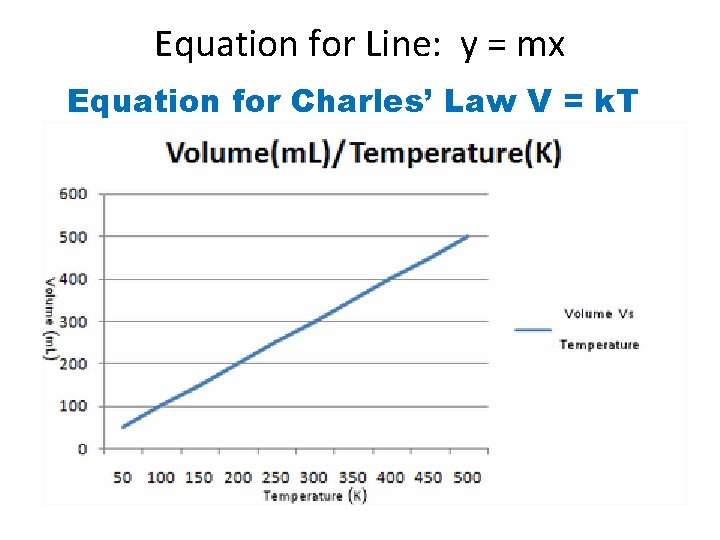
Equation for Line: y = mx Equation for Charles’ Law V = k. T

DERIVATION OF CHARLES’ LAW EQUATION IN TERMS OF V 1, T 1, V 2 AND T 2: • V = k. T k = V/T • At Volume, V 1 and Temperature, T 1 • V 1/T 1 = k • At same pressure and number of moles, the ratio of any other volume V 2 and Temperature T 2 must also equal k: V 2/T 2 = k • Thus V 1/T 1 = k = V 2/T 2 • V 1/T 1 = V 2/T 2 or T 1/V 1 = T 2/V 2 (at constant pressure and # of moles, n)

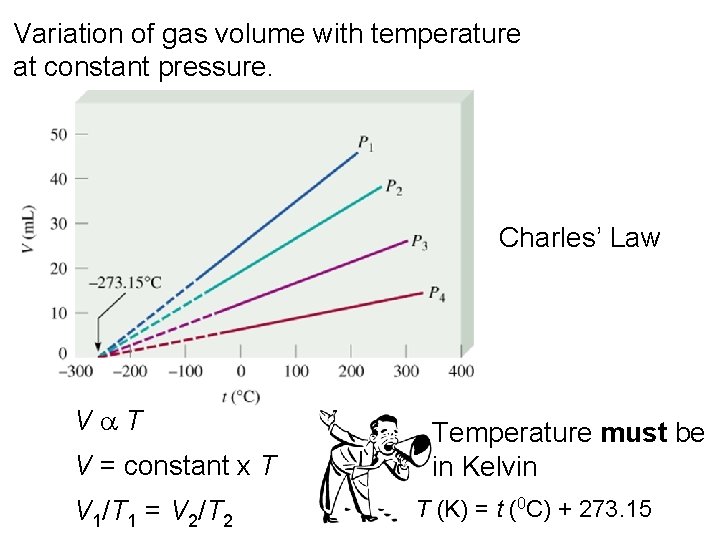
Variation of gas volume with temperature at constant pressure. Charles’ Law Va. T V = constant x T V 1/T 1 = V 2/T 2 Temperature must be in Kelvin T (K) = t (0 C) + 273. 15

A sample of carbon monoxide gas at 15 0 C. occupies 2. 58 L. The temperature is then raised to 38 0 C at constant pressure. Predict whether the volume will increase or decrease and than calculate the new volume. V 1/T 1 = V 2/T 2 V 2 = ? V 1 = 2. 58 L T 1 = 15 + 273 = 288 K V 1 x T 2 V 2 = = T 1 T 2 = 38 + 273 = 311 K 2. 58 L x 311 K 288 K = 2. 79 L

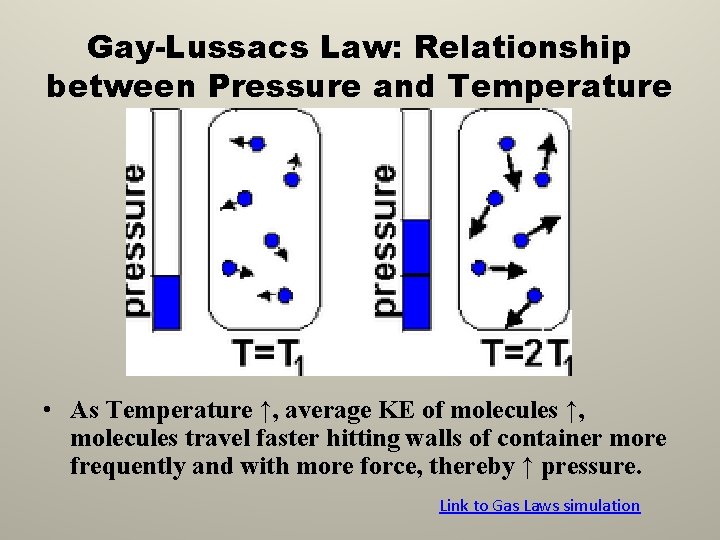
Gay-Lussacs Law: Relationship between Pressure and Temperature • As Temperature ↑, average KE of molecules ↑, molecules travel faster hitting walls of container more frequently and with more force, thereby ↑ pressure. Link to Gas Laws simulation

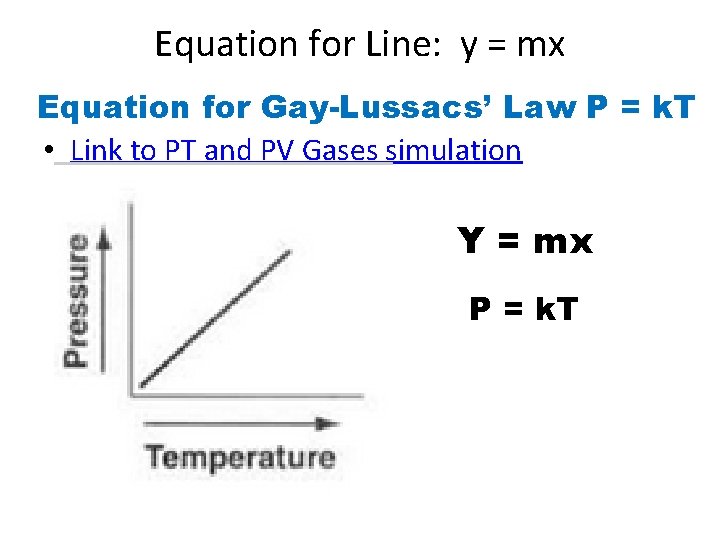
Equation for Line: y = mx Equation for Gay-Lussacs’ Law P = k. T • Link to PT and PV Gases simulation Y = mx P = k. T

DERIVATION OF GAY- LUSSAC’S LAW EQUATION IN TERMS OF P 1, T 1, P 2 AND T 2: • P = k. T k = P/T • At Volume, P 1 and Temperature, T 1 • P 1/T 1 = k • At same volume and number of moles, the ratio of any other pressure, P 2 and Temperature T 2 must also equal k: P 2/T 2 = k • Thus P 1/T 1 = k = P 2/T 2 • P 1/T 1 = P 2/T 2 or P 1/V 1 = P 2/V 2 (at constant volume and # of moles, n)

The pressure is a hydrogen tank is 3000. psi. If the temperature is cooled 20 0 C to 15 0 C at constant volume. Will the pressure increase or decrease? What is the final pressure of the gas? P 1 = 3000. psi T 1 = 20 + 273 =293 K P 2 = ? T 2 = 15 + 273 = 288 K P 1 P 2 = T 1 T 2 = 3000. psi x 288 K = 2950 psi (3 SF) P 2 = P 1 x 293 K T 1

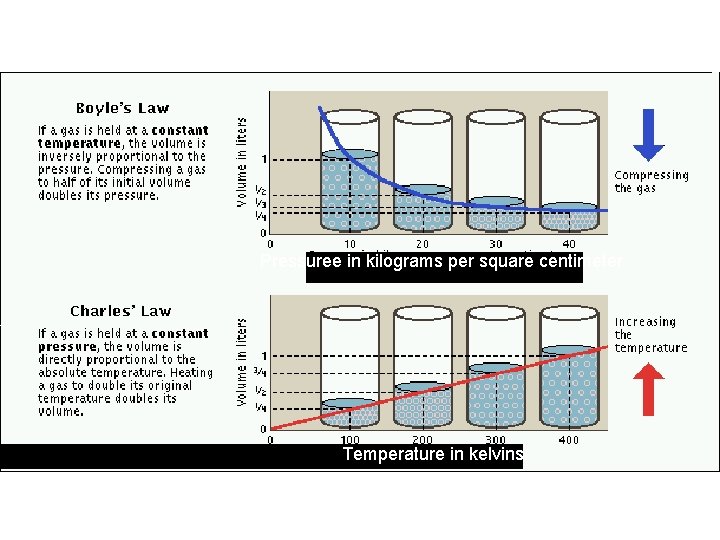
Pressuree in kilograms per square centimeter Temperature in kelvins

Equation for Line: y = mx Equation for Boyle’s Law P = k (1/V) V vs. P 1/V vs P Link to Boyle’s Law

DERIVATION OF BOYLE’S LAW EQUATION IN TERMS OF P 1, V 1, P 2 AND V 2: • P = k(1/V) k = PV • At Pressure, P 1 and Volume, V 1 • P 1 V 1 = k • At same temperature and number of moles, the ratio of any other volume P 1 and Volume V 2 must also equal k: P 2 V 2 = k • Thus P 1 V 1 = k = P 2 V 2 • P 1 V 1 = P 2 V 2 • (at constant temperature and # of moles, n)

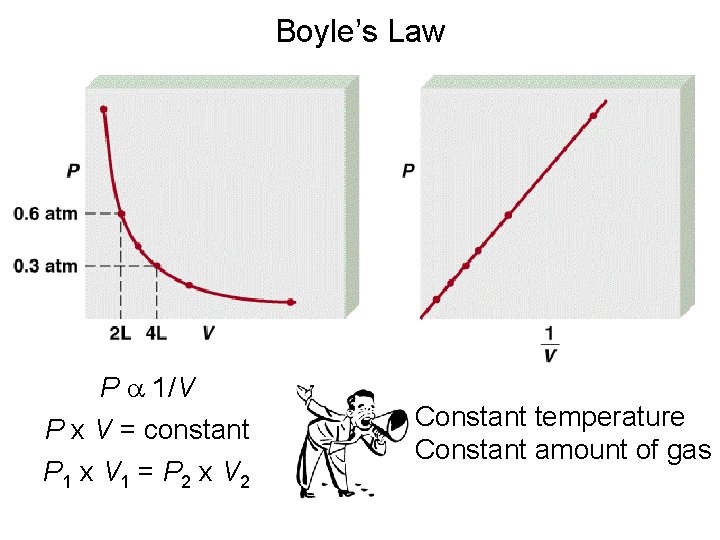
Boyle’s Law P a 1/V P x V = constant P 1 x V 1 = P 2 x V 2 Constant temperature Constant amount of gas

The pressure of a 1. 5 L sample of gas changes from 56 mm. Hg (torr) to 150. mm Hg (torr). Will the volume increase or decrease? Calculate the new volume P 1 x V 1 = P 2 x V 2 P 1 = 56 torr P 2 = 150 torr V 1 = 1. 5 L V 2 = ? L P 1 x V 1 56 torr x 1. 5 L V 2 = = 150 torr P 2 = 0. 56 L

COMBINED GAS LAW • • Combining all equations gives the combined gas law: P 1/T 1 = P 2/T 2 V 1/T 1 = V 2/T 2 P 1 x V 1 = P 2 x V 2 n, # of moles constant

At what temperature does 100. m. L of nitrogen at 27 0 C and 1. 13 atm occupy a volume of 500. m. L at a pressure of 1. 89 atm? P 1 = 1. 13 atm T 1 = 27 + 273 =300. K V 1 = 100. m. L P 1 P 2 = V 1 T 1 V 2 T 2 288 K = 1. 89 atm x T 2 293 K P 2 = 1. 89 atm T 2 = ? V 2 = 500. m. L T 2 = P 2 x V 1 P 1 x T 1 V 2 = 2950 psi (3 SF)