Derivatives definition and derivatives of various functions What

  • Slides: 32
Download presentation
Derivatives: definition and derivatives of various functions

Derivatives: definition and derivatives of various functions

What is a derivative? • A function • the rate of change of a

What is a derivative? • A function • the rate of change of a function • the slope of the line tangent to the curve

The tangent line single point of intersection

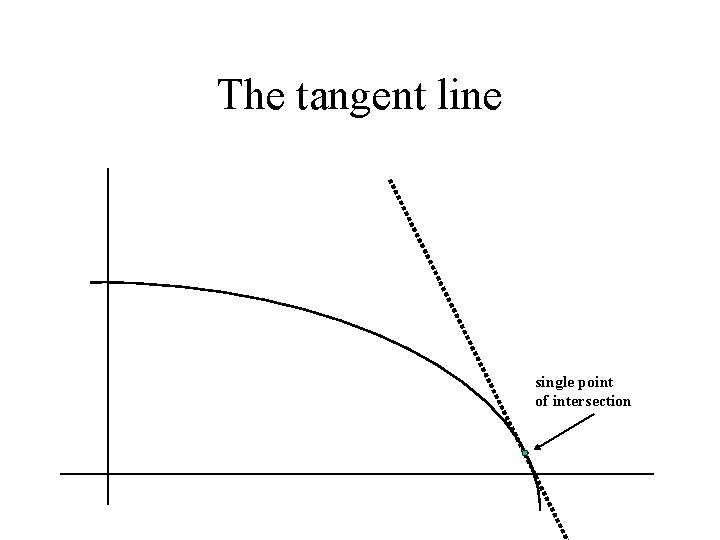
The tangent line single point of intersection

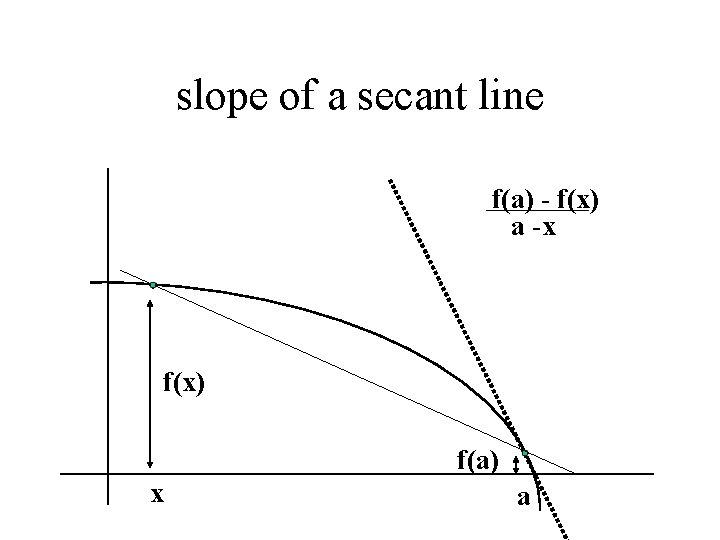
slope of a secant line f(a) - f(x) a -x f(x) f(a) x a

slope of a secant line f(a) - f(x) a -x f(x) f(a) x a

slope of a (closer) secant line f(a) - f(x) a-x f(x) f(a) x x

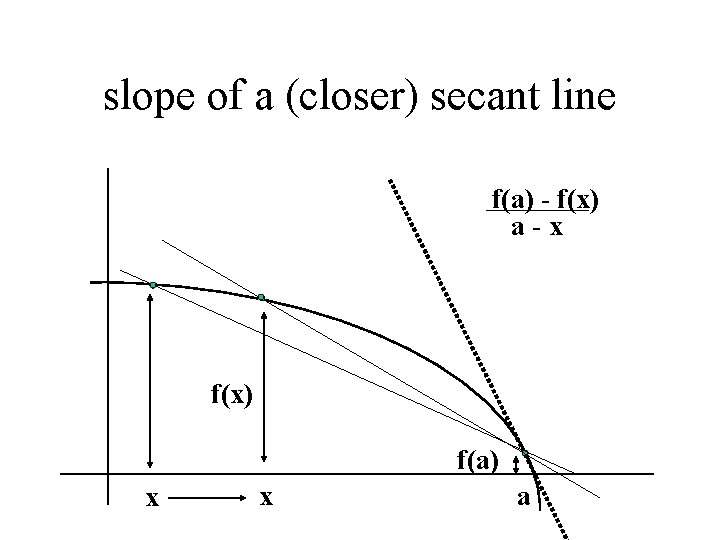
slope of a (closer) secant line f(a) - f(x) a-x f(x) f(a) x x a

closer and closer… a

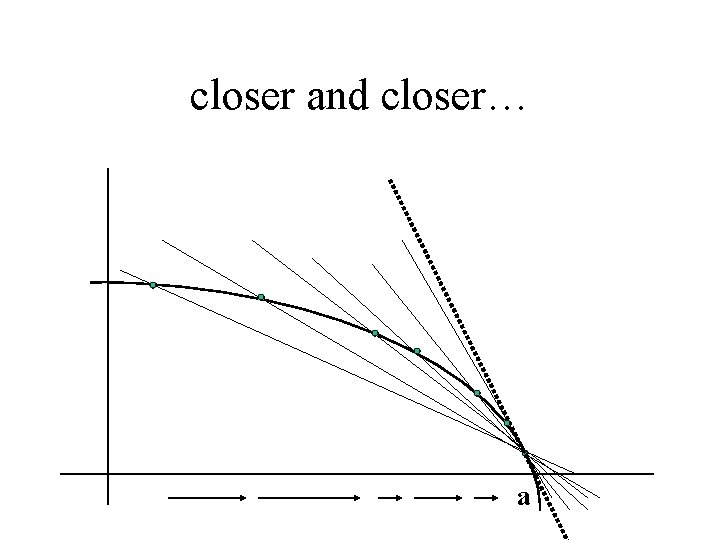
closer and closer… a

watch the slope. . .

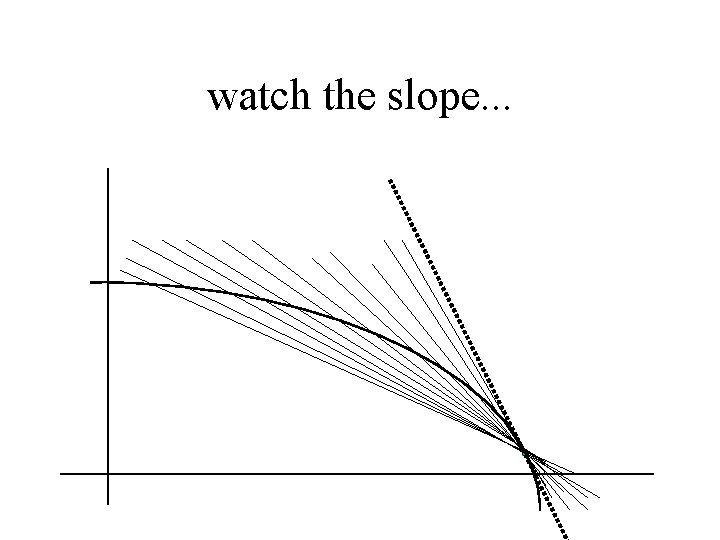
watch the slope. . .

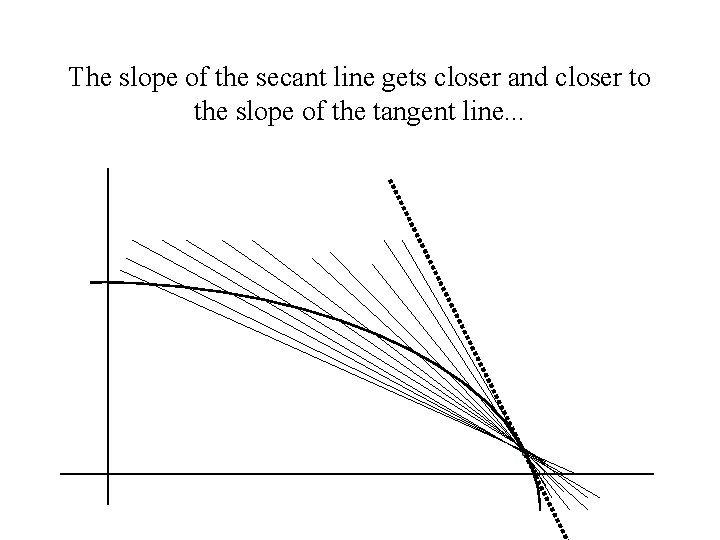
The slope of the secant line gets closer and closer to the slope of

The slope of the secant line gets closer and closer to the slope of the tangent line. . .

As the values of x get closer and closer to a! x a

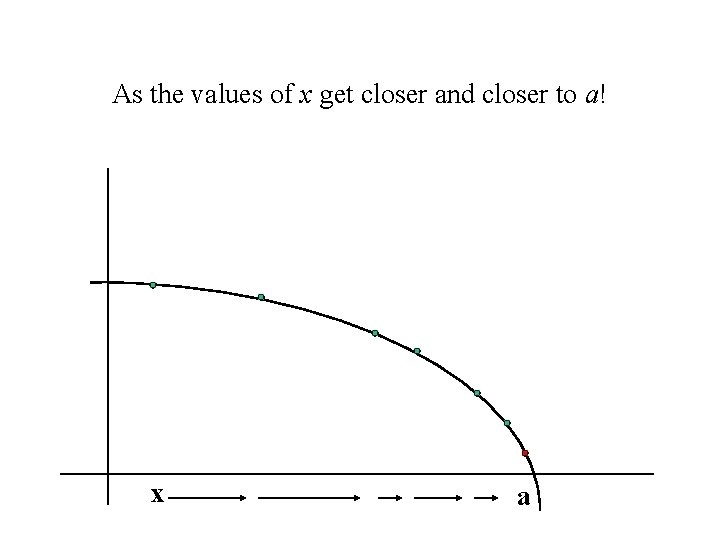
As the values of x get closer and closer to a! x a

The slope of the secant lines gets closer to the slope of the tangent

The slope of the secant lines gets closer to the slope of the tangent line. . . as the values of x get closer to a Translates to….

lim x as x goes to a a f(x) - f(a) x-a Equation for

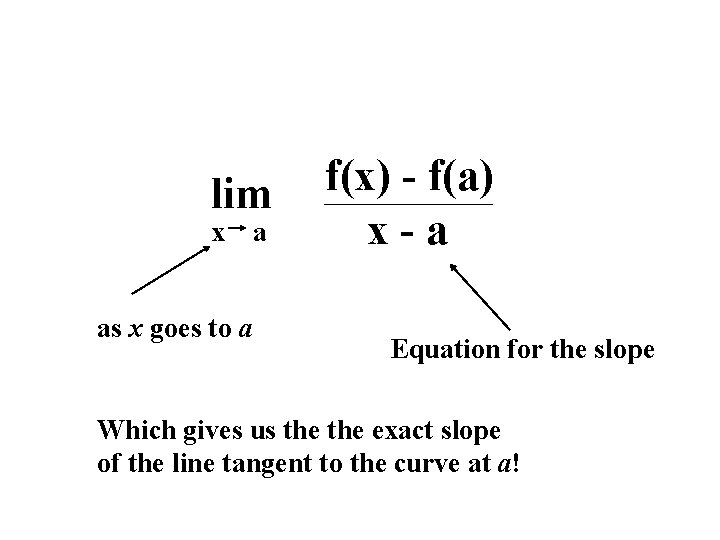
lim x as x goes to a a f(x) - f(a) x-a Equation for the slope Which gives us the exact slope of the line tangent to the curve at a!

The tangent line problem secant line (x, f(x)) is the point of tangency and

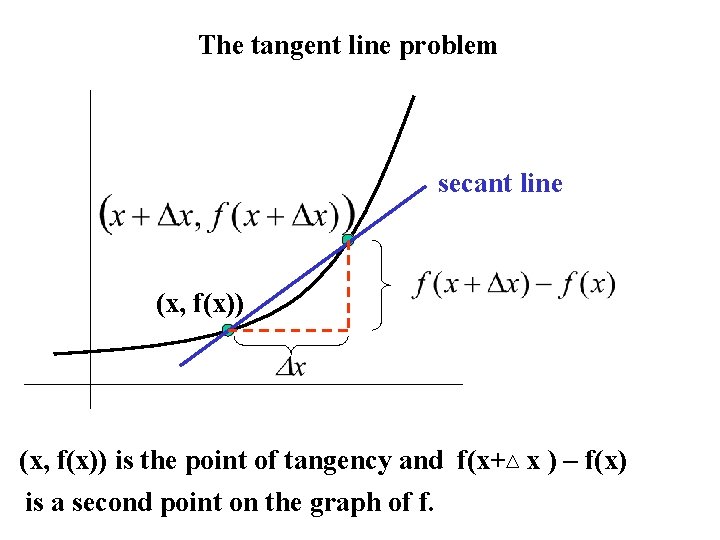
The tangent line problem secant line (x, f(x)) is the point of tangency and f(x+ x ) – f(x) is a second point on the graph of f.

The slope between these two points is Definition of Tangent Line with Slope m

The slope between these two points is Definition of Tangent Line with Slope m

Find the slope of the graph of f(x) = x 2 +1 at the

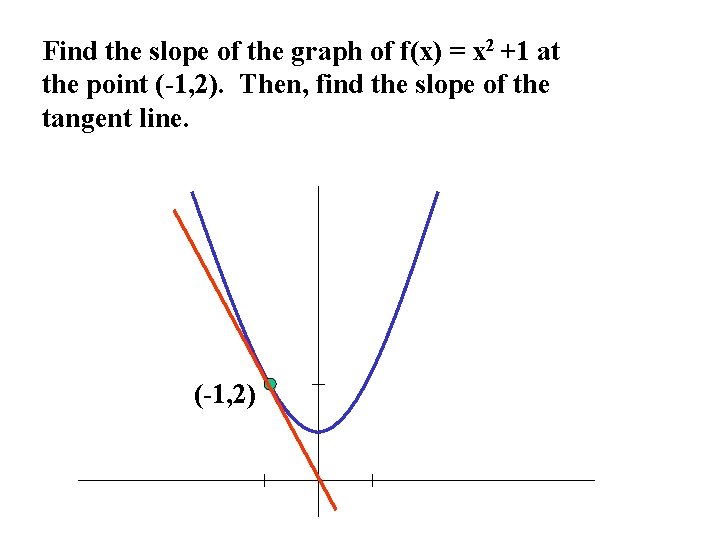
Find the slope of the graph of f(x) = x 2 +1 at the point (-1, 2). Then, find the slope of the tangent line. (-1, 2)

f(x) = x 2 + 1 Therefore, the slope at any point (x, f(x))

f(x) = x 2 + 1 Therefore, the slope at any point (x, f(x)) is given by m = 2 x What is the slope at the point (-1, 2)? m = -2

The limit used to define the slope of a tangent line is also used

The limit used to define the slope of a tangent line is also used to define of the two fundamental operations of calculus --- differentiation Definition of the Derivative of a Function f’(x) is read “f prime of x”

Find f’(x) for f(x) = and use the result to find the slope of

Find f’(x) for f(x) = and use the result to find the slope of the graph of f at the points (1, 1) & (4, 2). What happens at the point (0, 0)? 1

Derivative of a Function “the derivative of f with respect to x” “y

Derivative of a Function “the derivative of f with respect to x” “y prime” “the derivative of y with respect to x” “the derivative of f of x”

Differentiability. • To be differentiable, a function must be continuous and smooth. • Derivatives

Differentiability. • To be differentiable, a function must be continuous and smooth. • Derivatives will not exist at the following: corner vertical tangent cusp discontinuity

Differentiability: Intermediate value theorem • If a and b are any two points in

Differentiability: Intermediate value theorem • If a and b are any two points in an interval on which f is differentiable, then takes on every value between and Between a and b, must take on every value between. and

Rules of differentiation

Rules of differentiation

Differentiation: Function Types •

Differentiation: Function Types •

Differentiation: Function Types •

Differentiation: Function Types •

Differentiation: Function Types •

Differentiation: Function Types •

Rules of Differentiation •

Rules of Differentiation •

Rules of Differentiation •

Rules of Differentiation •

Rules of Differentiation •

Rules of Differentiation •

Rules of Differentiation •

Rules of Differentiation •

Examples of Composite Functions •

Examples of Composite Functions •

The Chain Rule of Composite Functions •

The Chain Rule of Composite Functions •

Examples •

Examples •

Session Problem Set •

Session Problem Set •

Module Derivatives and Related Accounting Issues Derivatives DerivativesModule Derivatives and Related Accounting Issues Derivatives Derivatives
Derivatives and Gradients Derivatives Derivatives tell us whichDerivatives and Gradients Derivatives Derivatives tell us which
CREDIT DERIVATIVES WHAT ARE CREDIT DERIVATIVES Credit derivativesCREDIT DERIVATIVES WHAT ARE CREDIT DERIVATIVES Credit derivatives
Derivatives part I 1 Derivatives Derivatives are financialDerivatives part I 1 Derivatives Derivatives are financial
3 DERIVATIVES DERIVATIVES 3 4 Derivatives of Trigonometric3 DERIVATIVES DERIVATIVES 3 4 Derivatives of Trigonometric
Derivatives part I 1 Derivatives Derivatives are financialDerivatives part I 1 Derivatives Derivatives are financial
Derivatives part I 1 Derivatives Derivatives are financialDerivatives part I 1 Derivatives Derivatives are financial
TRANSCENDENTAL FUNCTIONS Transcendental Functions Inverse Functions Derivatives ofTRANSCENDENTAL FUNCTIONS Transcendental Functions Inverse Functions Derivatives of
DERIVATIVES OF INVERSE TRIG FUNCTIONS To get derivativesDERIVATIVES OF INVERSE TRIG FUNCTIONS To get derivatives
Second Order Partial Derivatives Since derivatives of functionsSecond Order Partial Derivatives Since derivatives of functions
3 DERIVATIVES DERIVATIVES The functions that we have3 DERIVATIVES DERIVATIVES The functions that we have
3 DERIVATIVES DERIVATIVES The functions that we have3 DERIVATIVES DERIVATIVES The functions that we have
3 DERIVATIVES DERIVATIVES The functions that we have3 DERIVATIVES DERIVATIVES The functions that we have
3 3 DERIVATIVES OF TRIGONOMETRIC FUNCTIONS DERIVATIVES OF3 3 DERIVATIVES OF TRIGONOMETRIC FUNCTIONS DERIVATIVES OF
Powerpoint Jeopardy Definition of Derivatives Basic Derivatives EquationPowerpoint Jeopardy Definition of Derivatives Basic Derivatives Equation
Welcome Todays Topic is Derivatives Derivatives Limit DefinitionWelcome Todays Topic is Derivatives Derivatives Limit Definition
SQL Functions SingleRow Functions MultipleRow Functions Character FunctionsSQL Functions SingleRow Functions MultipleRow Functions Character Functions
Functions Functions l l Evaluating Functions Graphing FunctionsFunctions Functions l l Evaluating Functions Graphing Functions
13 VECTOR FUNCTIONS VECTOR FUNCTIONS 13 2 Derivatives13 VECTOR FUNCTIONS VECTOR FUNCTIONS 13 2 Derivatives
8 Transcendental Functions Logarithms Exponential Functions Derivatives of8 Transcendental Functions Logarithms Exponential Functions Derivatives of
Applications and layered architectures Various services various applicationsApplications and layered architectures Various services various applications
Derivatives and Securitization Both Derivatives and Securitization representDerivatives and Securitization Both Derivatives and Securitization represent
2 LIMITS AND DERIVATIVES LIMITS AND DERIVATIVES 22 LIMITS AND DERIVATIVES LIMITS AND DERIVATIVES 2
2 LIMITS AND DERIVATIVES LIMITS AND DERIVATIVES We2 LIMITS AND DERIVATIVES LIMITS AND DERIVATIVES We