Derivative Practice Definition Applied Family of f Of











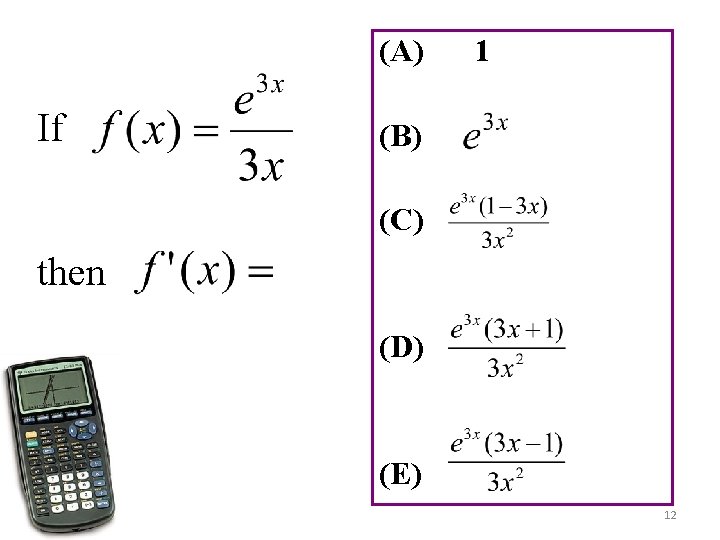





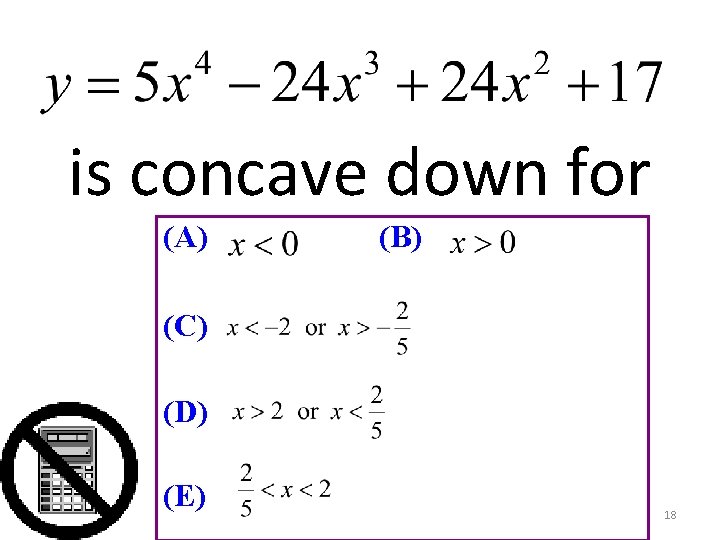

















![The maximum value of on the interval [0, 2] is (A) (B) (C) (D) The maximum value of on the interval [0, 2] is (A) (B) (C) (D)](https://slidetodoc.com/presentation_image/bd608256dfe0df9c7993b889e350e084/image-38.jpg)








![If f is continuous on [2, 5] and differentiable on (2, 5) with f(2) If f is continuous on [2, 5] and differentiable on (2, 5) with f(2)](https://slidetodoc.com/presentation_image/bd608256dfe0df9c7993b889e350e084/image-48.jpg)



- Slides: 51

Derivative Practice Definition Applied Family of f: Of the Derivatives f & f’’ Derivative NO Calc Applied Derivatives WITH Calc 100 100 100 200 200 200 300 300 300 400 400 400 500 500 500 1


Solution (100 pts) E. 3

If then is (A) (B) (C) (D) (E) 4

Solution (200 pts) A. 5

If then (A) 8 (B) 2 (C) -2 (D) -3 (E) -8 6

Solution (300 pts) C. -2 7

If what is the value of at (3, 4) (A) (B) (C) (D) (E) 8

Solution (400 pts) A. 9

Let f and g be differentiable functions with the following properties: I. for all x II. If and then (A) (B) (C) (D) 0 (E) 2 10

Solution (500 pts) E. 2 11
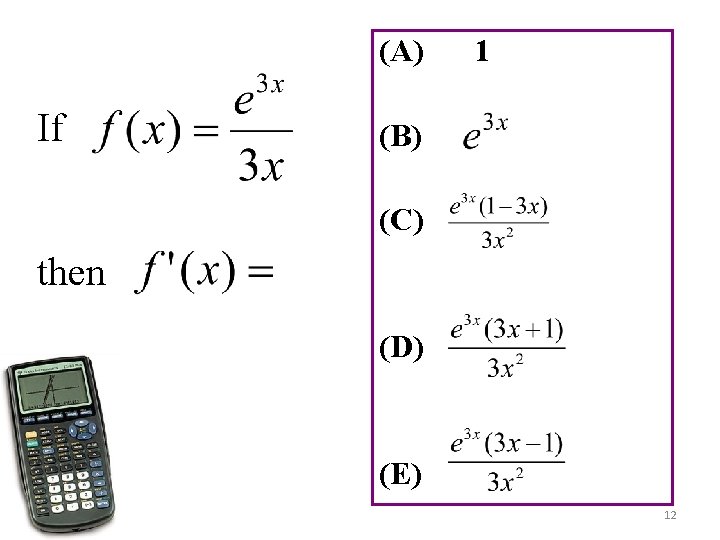
(A) If 1 (B) (C) then (D) (E) 12

Solution (100 pts) E 13

The graph of the function changes concavity at x = (A) 3. 29 (B) 2. 21 (C) 1. 34 (D) 0. 41 (E) -0. 39 14

Solution (200 pts) B 2. 21 15

Let f be a function such that For all x in the closed interval [3, 4] with selected values shown in the table. Which of the following must be true about X 3. 2 3. 3 3. 4 3. 5 f(x) 2. 48 2. 68 2. 86 3. 03 (A) (B) (C) (D) (E) 16

Solution (300 pts) D 17
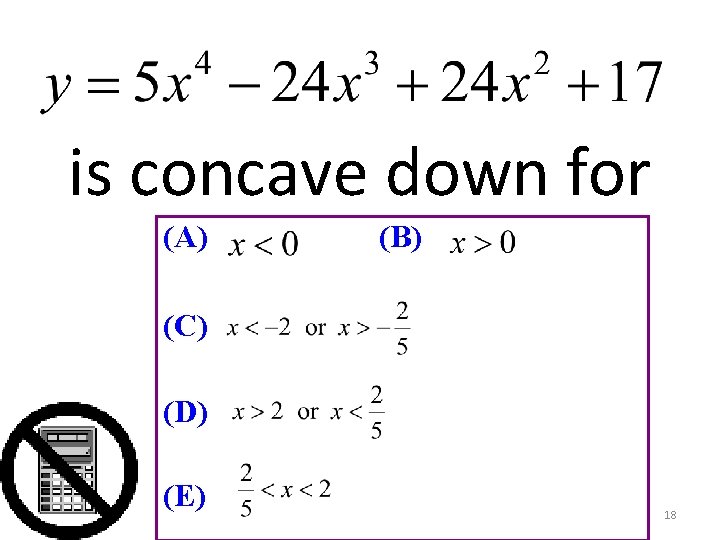
is concave down for (A) (B) (C) (D) (E) 18

Solution (400 pts) E 19

What are all the values of x for which the function f defined by is increasing? (A) There are no such values of x (B) (C) (D) (E) All values of x 20

Solution (500 pts) D. 21

Let For what value of x does (A) (B) (C) (D) (E) -2 -1 1 2 4 22

Solution (100 pts) D 2 23

Let f be a function such that Which of the following must be true? I. f is continuous at x = 7 II. f is differentiable at x = 7 III. The derivative of f is continuous at x = 7 (A) (B) (C) (D) (E) I only I and III only II and III only 24

Solution (200 pts) C I and II only 25

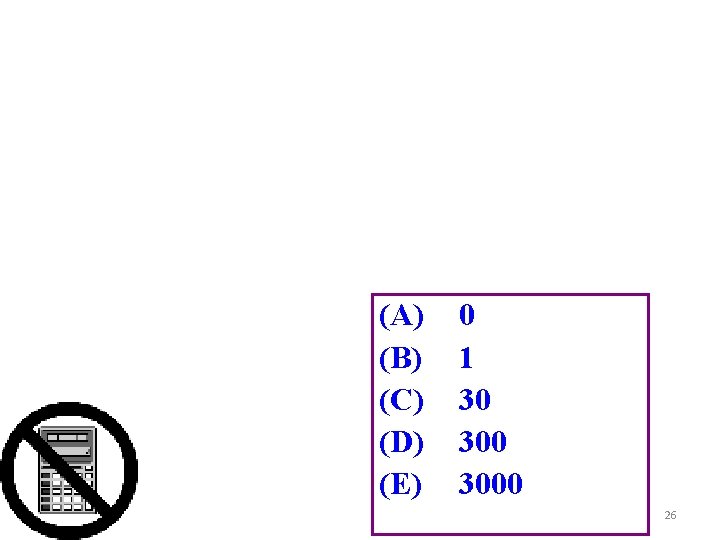
(A) (B) (C) (D) (E) 0 1 30 3000 26

Solution (300 pts) D. 300 27

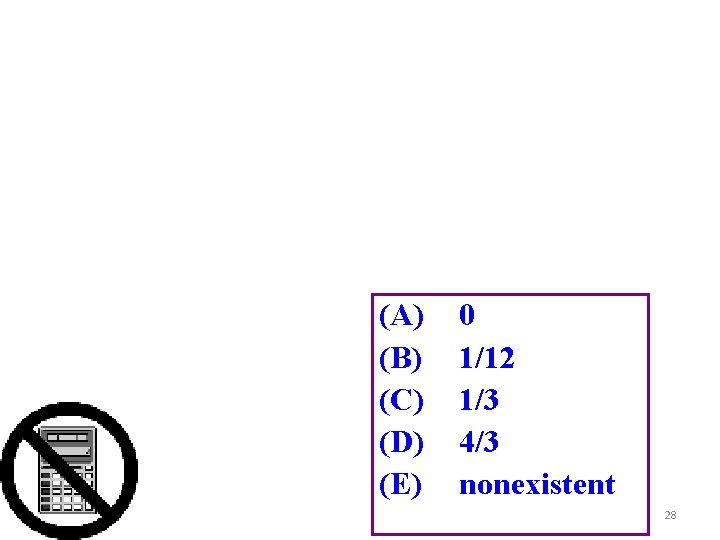
(A) (B) (C) (D) (E) 0 1/12 1/3 4/3 nonexistent 28

Solution (400 pts) B. 1/12 29


Solution (500 pts) B. 31

An equation of the line tangent to the graph of at is (A) (B) (C) (D) (E) 32

Solution (100 pts) C. 33

Let then (A) (B) (C) (D) (E) -1 0 1 2 nonexistent 34

Solution (200 pts) A. -1 35

The minimum acceleration attained on the interval 0 ≤ t ≤ 4 by the particle whose velocity is given by is (A) (B) (C) (D) (E) -16 -10 -8 -25/3 -3 36

Solution (300 pts) D. -25/3 37
![The maximum value of on the interval 0 2 is A B C D The maximum value of on the interval [0, 2] is (A) (B) (C) (D)](https://slidetodoc.com/presentation_image/bd608256dfe0df9c7993b889e350e084/image-38.jpg)
The maximum value of on the interval [0, 2] is (A) (B) (C) (D) (E) 25 -7 -2 0 2 38

Solution (400 pts) D. 0 39

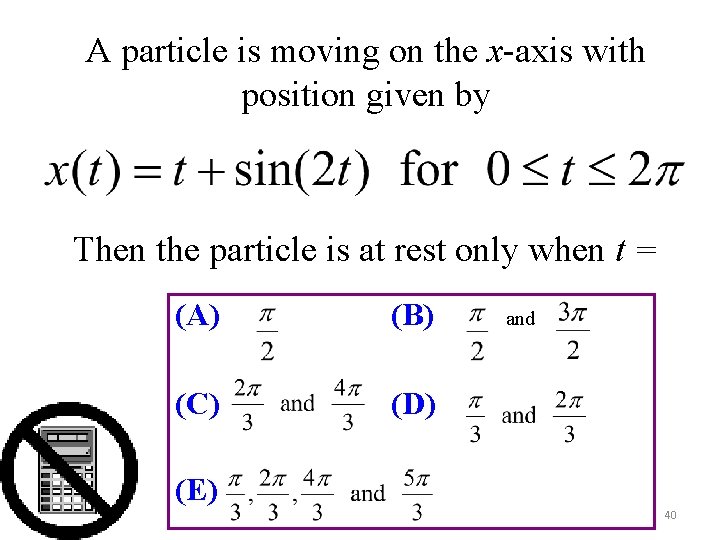
A particle is moving on the x-axis with position given by Then the particle is at rest only when t = (A) (B) (C) (D) and (E) 40

Solution (500 pts) E. 41

Which of the following is an equation of the line tangent to the graph of at the point where (A) (B) (C) (D) (E) 42

Solution (100 pts) A. 43

The side of a cube is increasing at a constant rate of 0. 2 centimeter per second. In terms of the surface area S, what is the rate of change of the volume of the cube, in cubic centimeters per second? (A) (B) (C) (D) (E) 0. 1 S 0. 2 S 0. 6 S 0. 04 S 0. 008 S 44

Solution (200 pts) A. 0. 1 S 45

Let f be a function that is differentiable on the open interval (-3, 7). If f(-1) = 4, f(2) = -5 and f(6) = 8, which of the following must be true? I. f has at least 2 zeroes II. f has a relative minimum at x = 2 III. For some c, 2 < c < 6, f(c) = 4 (A) I only (B) II only (C) I and II only (D) I and III only (E) I, II, and III 46

Solution (300 pts) D. I and III only 47
![If f is continuous on 2 5 and differentiable on 2 5 with f2 If f is continuous on [2, 5] and differentiable on (2, 5) with f(2)](https://slidetodoc.com/presentation_image/bd608256dfe0df9c7993b889e350e084/image-48.jpg)
If f is continuous on [2, 5] and differentiable on (2, 5) with f(2) = -4 and f(5) = 14, which of the following statements must be true? I. f(x) = 6 has a solution in (2, 5) II. f’(x) = 6 has a solution in (2, 5) III. f’’(x) = 6 has a solution in (2, 5) (A) I only (B) II only (C) I and II only (D) I and III only (E) I, II, and III 48

Solution (400 pts) C. I and II only 49

At the moment that a rectangle is 8 feet long and 3 feet wide, its length is increasing at 0. 5 feet/minute and its width is decreasing at 1. 5 feet/minute. The area is (A) (B) (C) (D) (E) decreasing at 10. 5 square feet/minute increasing at 13. 5 square feet/minute increasing at 8. 5 square feet/minute decreasing at 0. 75 square feet/minute 50

Solution (500 pts) (A) decreasing at 10. 5 square feet/minute 51