Depth Increment in IDA Ling Zhao Dept of

  • Slides: 15
Download presentation
Depth Increment in IDA* Ling Zhao Dept. of Computing Science University of Alberta July

Depth Increment in IDA* Ling Zhao Dept. of Computing Science University of Alberta July 4, 2003

Outline l Introduction l Examples l Modifications on IDA* l Analytical Model l Experimental

Outline l Introduction l Examples l Modifications on IDA* l Analytical Model l Experimental results l Work to do l Conclusions

Introduction l In some single-agent search problems with very low branching factors (less than

Introduction l In some single-agent search problems with very low branching factors (less than 2), the generic IDA* typically visits many more nodes than A*. l Branching factor: b solution length: s A* -- bs IDA* -- b 1+b 2 +… +bs = (bs+1 -b)/(b-1) when bs is large enough, IDA* visits about 1/(b-1) times more nodes than A*.

Examples Overhead = 1/(1 -b) PCP: b = 1. 120 overhead = 8. 33

Examples Overhead = 1/(1 -b) PCP: b = 1. 120 overhead = 8. 33 Pathfinding: b is very close to 1 (? ) overhead > 30

How to solve the problem? l Depth is increased by more than one in

How to solve the problem? l Depth is increased by more than one in each iteration. cons: less redundant work pros: may need to search nodes with f value greater than solution length. Modification on generic IDA*(ensure optimality): when a solution is found, update the search threshold and keep searching.

Analytical model Assumptions: l search tree grows perfectly in an exponential series (1<b<2, s

Analytical model Assumptions: l search tree grows perfectly in an exponential series (1<b<2, s is very large) l need to find all optimal solutions l depth increment is a constant

A* - bs Analytical model IDA* - (bs+1 -b)/(b-1) -> bs+1/(b-1) IDA*’- (b(i+1)c- bc)/

A* - bs Analytical model IDA* - (bs+1 -b)/(b-1) -> bs+1/(b-1) IDA*’- (b(i+1)c- bc)/ (bc -1) -> b(i+1)c/ (bc -1) (ic = k+s) = bs * bk+c / (bc -1) overhead = bk+c / (bc -1) -1 Iteration 1: bc c solution length s Iteration 2 : b 2 c Iteration i-1: b(i-1)c k Iteration i: bic

overhead = bk+c / (bc -1) – 1 worst case (k=c): Min(overhead)=3 when bc

overhead = bk+c / (bc -1) – 1 worst case (k=c): Min(overhead)=3 when bc = 2 best case (k=0): Min(overhead)->0 when bc -> +infinity average case (k=c/2): Min(overhead)=1. 598 when bc = 3 Iteration 1: bc c solution length s Iteration 2 : b 2 c Iteration i-1: b(i-1)c k Iteration i: bic

overhead = bk+c / (bc -1) – 1 another average case: only shadowed area

overhead = bk+c / (bc -1) – 1 another average case: only shadowed area is visited (suppose it is 50% of the over-searched area), and k=c/2 Min(overhead) = 1. 1 when bc =2. 28 Iteration 1: bc c solution length s Iteration 2 : b 2 c Iteration i-1: b(i-1)c k Iteration i: bic

Experimental results l 200 difficult PCP instances k = 45%i x = 20% of

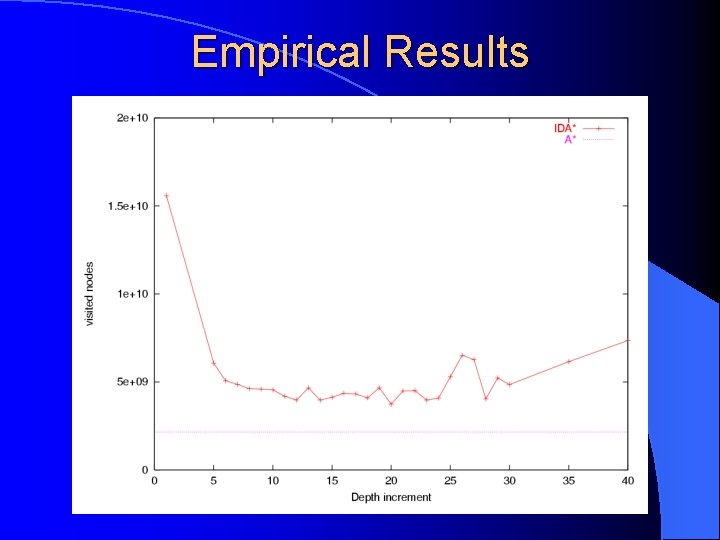
Experimental results l 200 difficult PCP instances k = 45%i x = 20% of over-searched area From the model: Min(overhead) = 0. 81 when bc = 7. 70 Empirically: Min(overhead)=0. 67 when c=20

Empirical Results

Empirical Results

Further thoughts Decrease overhead of IDA*’ 1. node overhead - better heuristics (look ahead)

Further thoughts Decrease overhead of IDA*’ 1. node overhead - better heuristics (look ahead) 2. right increment - very specific to problems 3. variable increment? ? ?

Work to do l Test the impact from better heuristics (lookahead) l Apply the

Work to do l Test the impact from better heuristics (lookahead) l Apply the idea to other problems - pathfinding? - two-player games with low bf - sliding puzzles (15, 24 -puzzles)? l Better statistical methods to compare analytical and empirical results

Summary Search problems with very low branching factors receive relatively less attention. difficult problem

Summary Search problems with very low branching factors receive relatively less attention. difficult problem => high/medium bf l PCP is a good domain to test algorithms for problems with low bf l IDA* with large depth increment performs much better in some problems with low branching factor (1<b<2) and typically very long solution lengths. l IDA*’ is almost cost-free l

A Simple Example of PCP Instance 1 2 3 100 1 00 Rules: 100

A Simple Example of PCP Instance 1 2 3 100 1 00 Rules: 100 pair 1: 1 1001 pair 3: 1001100 pair 1: 1001 pair 1: 100100 10011 1. select pairs 1001001 pair 3: 1001100 2. make the concatenated top string and bottom string identical. pair 2: 100100100 pair 2: 1001100100100

Planner Overview Increment Management The Increment Management screenPlanner Overview Increment Management The Increment Management screen
Repetition Increment Decrement Increment Decrement num Toppings numRepetition Increment Decrement Increment Decrement num Toppings num
Increment and Decrement The increment and decrement operatorsIncrement and Decrement The increment and decrement operators
Tax Increment Refinancing Zone TIRZ Presentation Tax IncrementTax Increment Refinancing Zone TIRZ Presentation Tax Increment
Increment Operator To increment a variable X byIncrement Operator To increment a variable X by
Planner Overview 2015 Increment Management The Increment ManagementPlanner Overview 2015 Increment Management The Increment Management
Tax Increment Refinancing Zone TIRZ Presentation Tax IncrementTax Increment Refinancing Zone TIRZ Presentation Tax Increment
Program Increment 2 Increment Demo 27 juni 2017Program Increment 2 Increment Demo 27 juni 2017
Increment Operator To increment a variable X byIncrement Operator To increment a variable X by
Increment and Decrement Operators Increment and Decrement OperationsIncrement and Decrement Operators Increment and Decrement Operations
Finding depth 1 Overview Depth from stereo DepthFinding depth 1 Overview Depth from stereo Depth
Ida B Wells A Red Record Background IdaIda B Wells A Red Record Background Ida
Meunarodno udruenje za razvoj IDA js Uvod IDAMeunarodno udruenje za razvoj IDA js Uvod IDA
FOTOSINTESIS PHOTOSYNTHESIS by IDA RIANAWATY Copyright2009 by IdaFOTOSINTESIS PHOTOSYNTHESIS by IDA RIANAWATY Copyright2009 by Ida