Depth First Search Depth First Search Assume unweighted
















- Slides: 106

Depth First Search

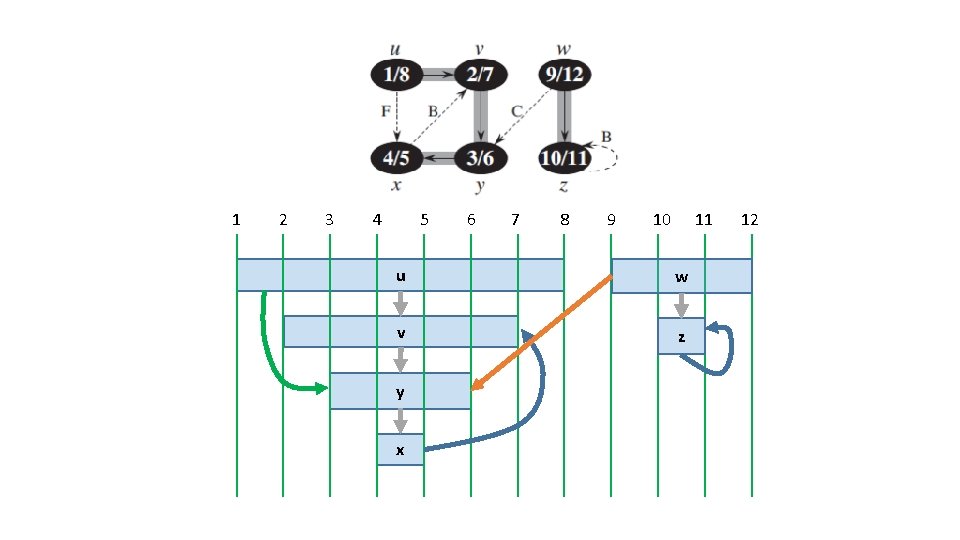
Depth First Search • Assume unweighted directed graph (allow self loops)








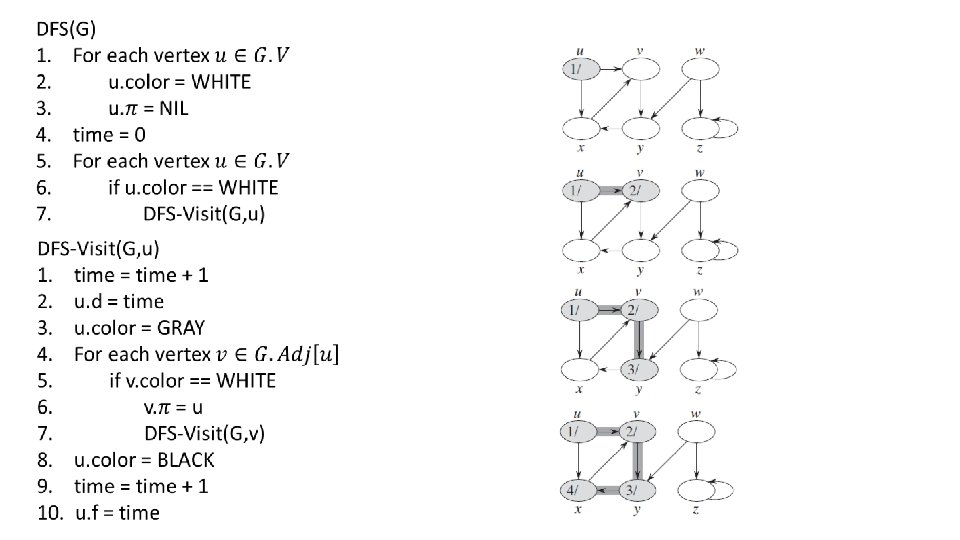
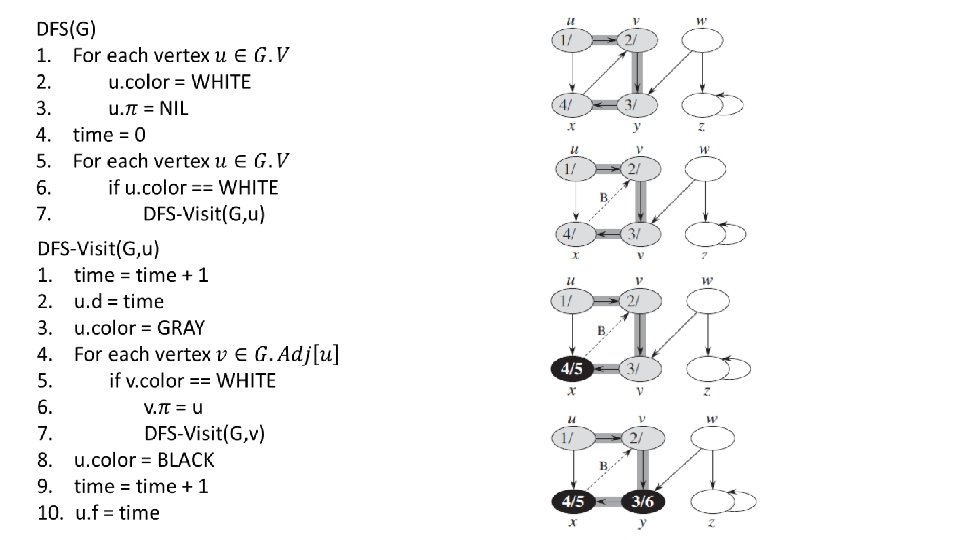
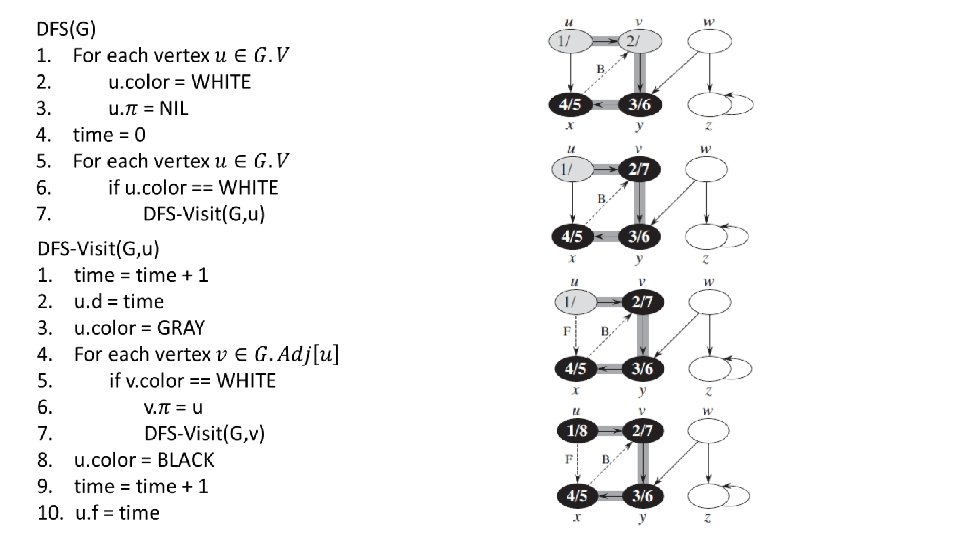
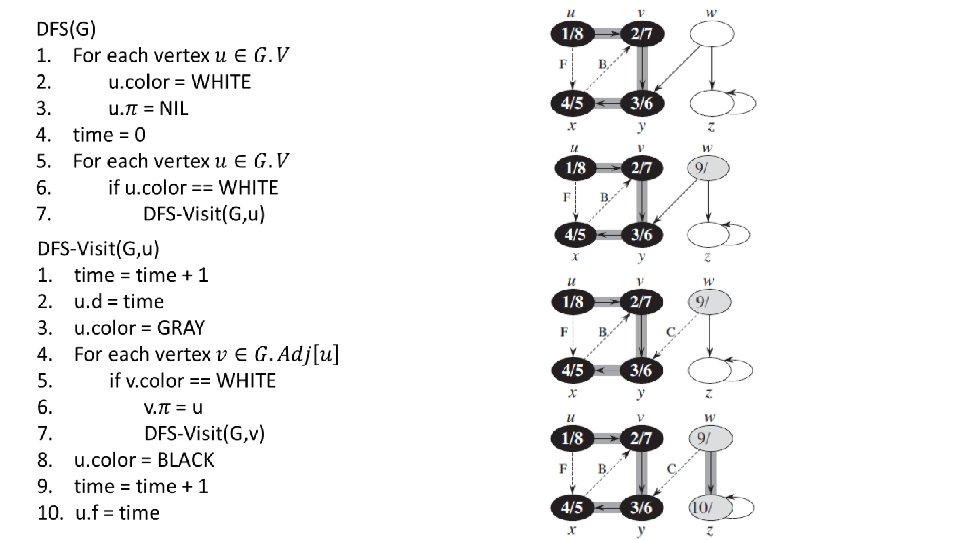
Proof: It corresponds to the structure of the recursive calls to DFS-Visit

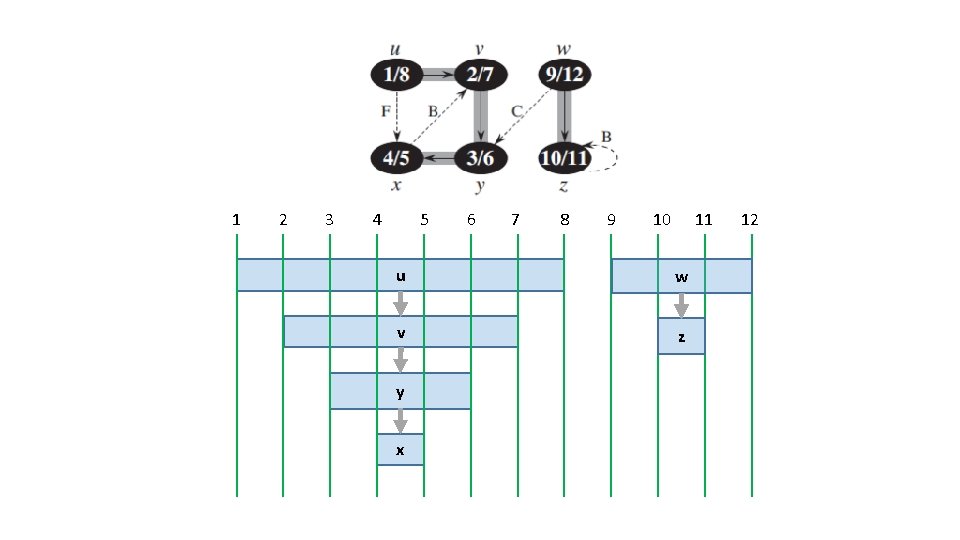
1 2 3 4 5 6 7 8 9 10 11 u w v z y x 12

Proof: It corresponds to the structure of the recursive calls to DFS-Visit

Proof: It corresponds to the structure of the recursive calls to DFS-Visit

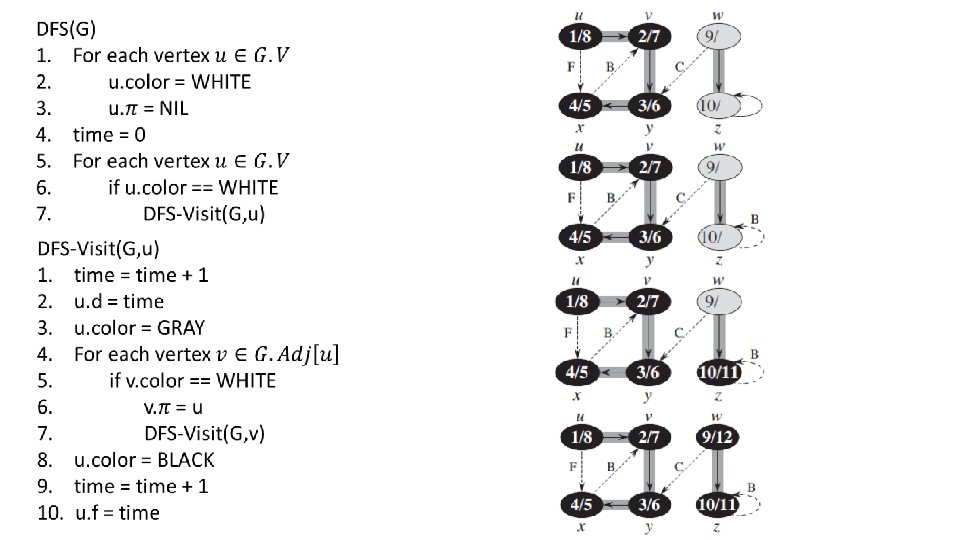
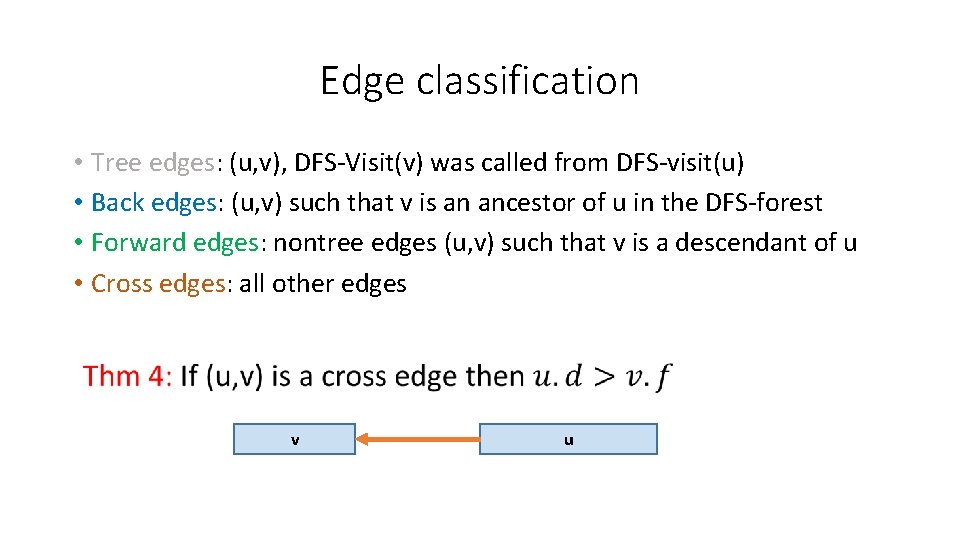
Edge classification • Tree edges: (u, v), DFS-Visit(v) was called from DFS-visit(u) • Back edges: (u, v) such that v is an ancestor of u in the DFS-forest

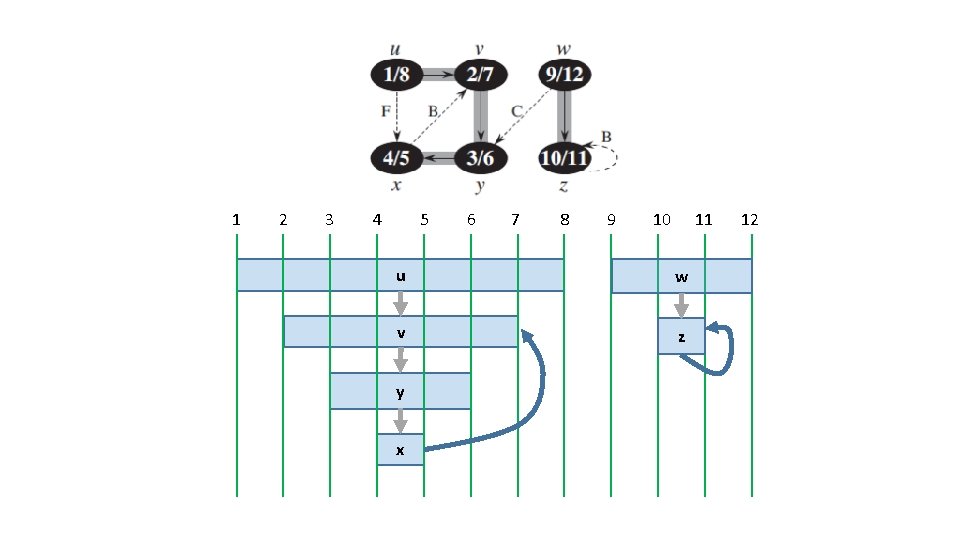
1 2 3 4 5 6 7 8 9 10 11 u w v z y x 12

Edge classification • Tree edges: (u, v), DFS-Visit(v) was called from DFS-visit(u) • Back edges: (u, v) such that v is an ancestor of u in the DFS-forest • Forward edges: nontree edges (u, v) such that v is a descendant of u

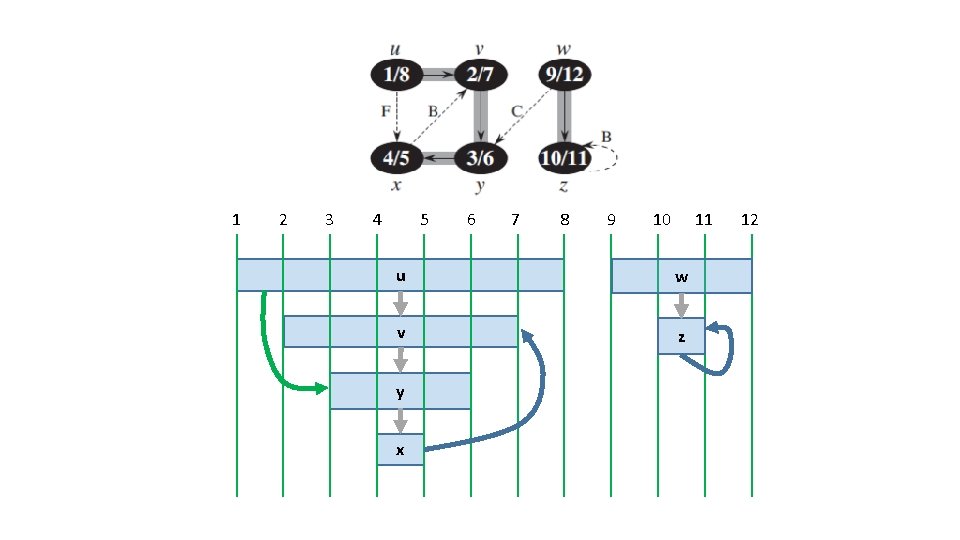
1 2 3 4 5 6 7 8 9 10 11 u w v z y x 12

Edge classification • Tree edges: (u, v), DFS-Visit(v) was called from DFS-visit(u) • Back edges: (u, v) such that v is an ancestor of u in the DFS-forest • Forward edges: nontree edges (u, v) such that v is a descendant of u • Cross edges: all other edges

1 2 3 4 5 6 7 8 9 10 11 u w v z y x 12

Edge classification • Tree edges: (u, v), DFS-Visit(v) was called from DFS-visit(u) • Back edges: (u, v) such that v is an ancestor of u in the DFS-forest • Forward edges: nontree edges (u, v) such that v is a descendant of u • Cross edges: all other edges v u

Classify as we go. . •

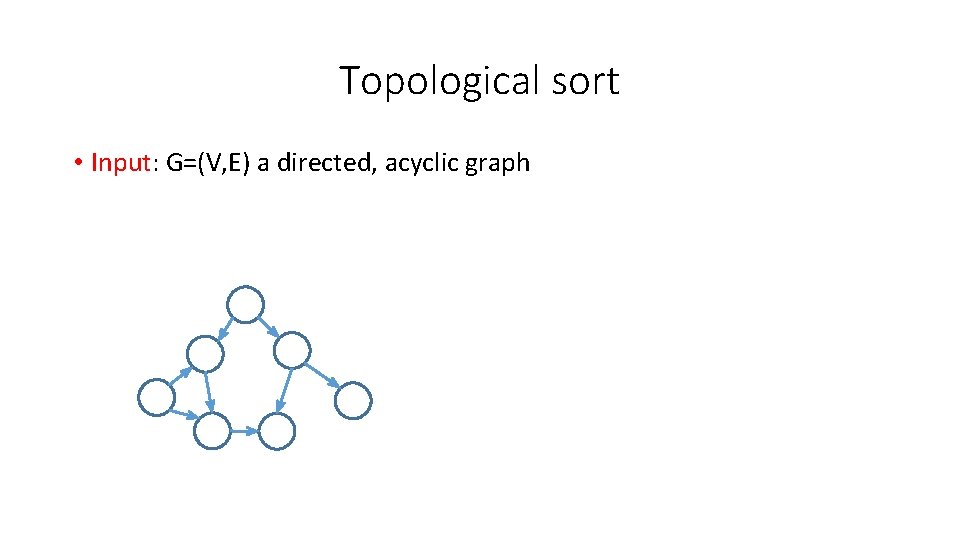
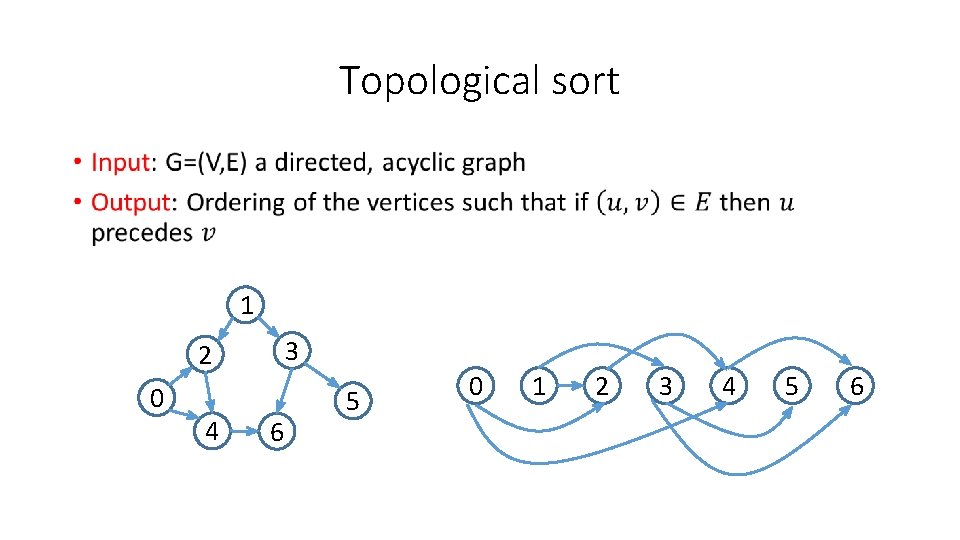
Topological sort • Input: G=(V, E) a directed, acyclic graph

Topological sort • 1 3 2 0 4 6 5 0 1 2 3 4 5 6

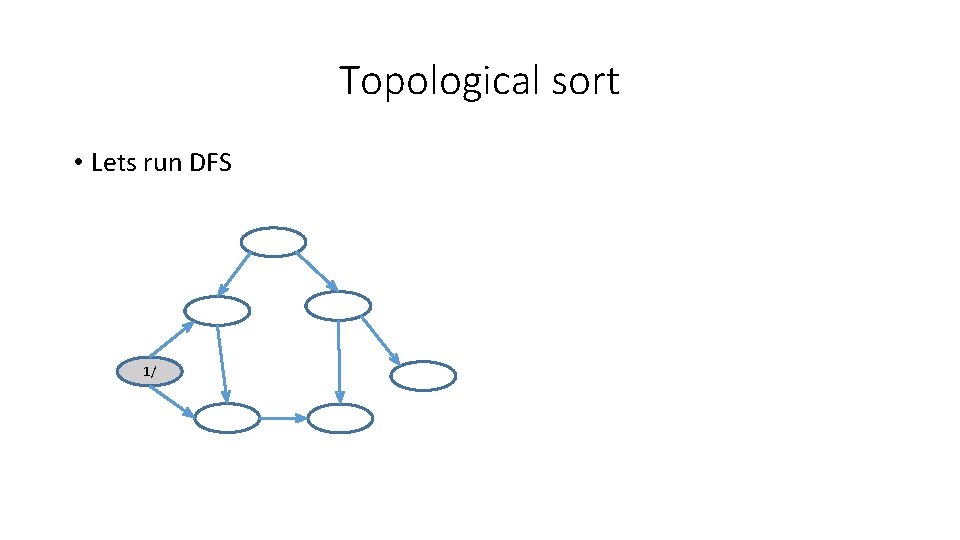
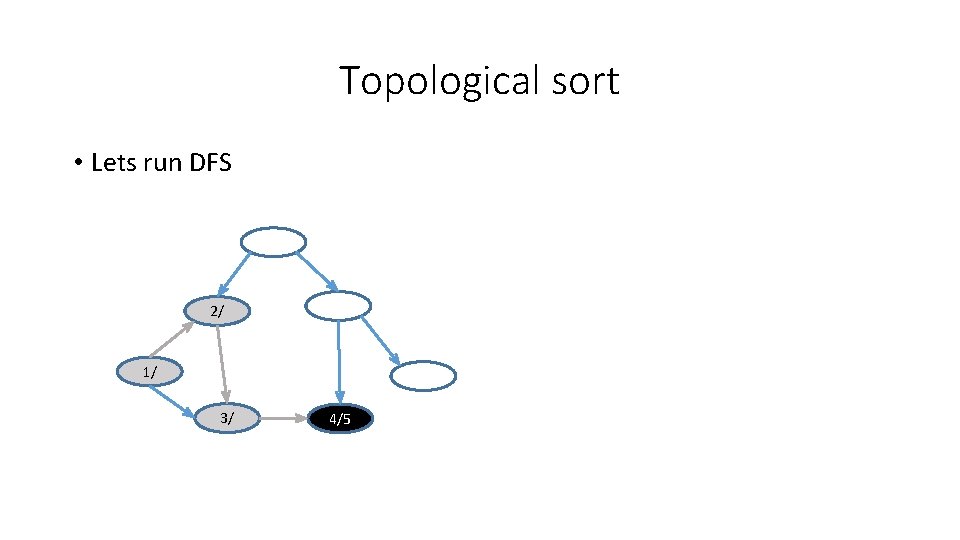
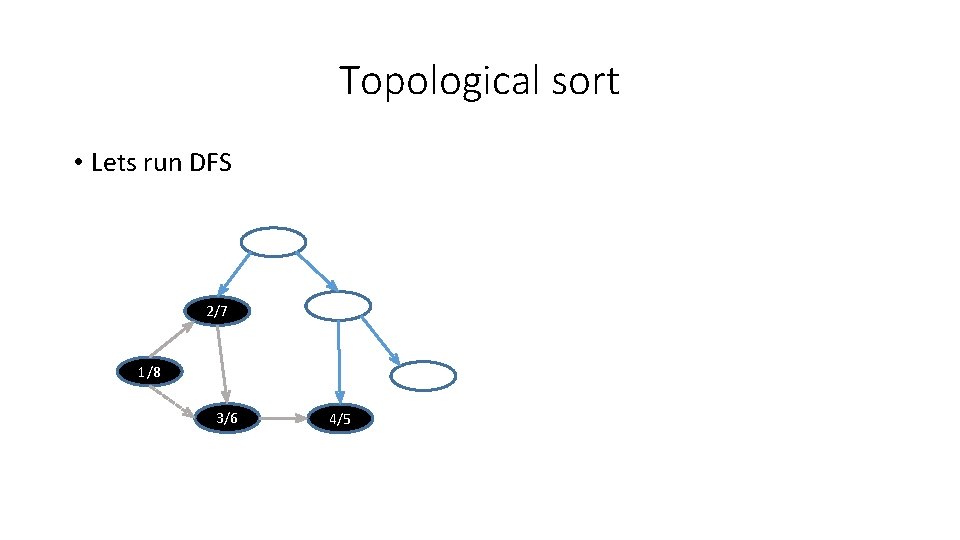
Topological sort • Lets run DFS 1/

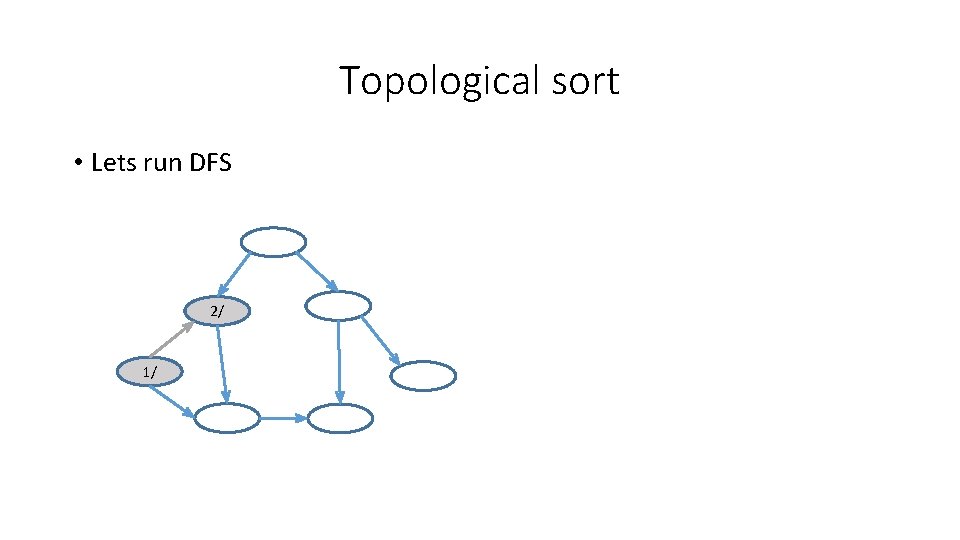
Topological sort • Lets run DFS 2/ 1/

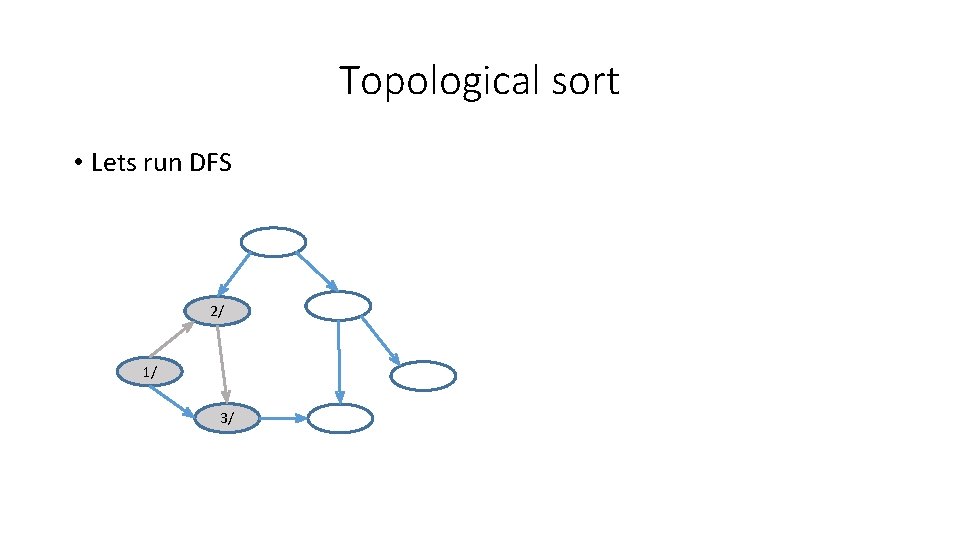
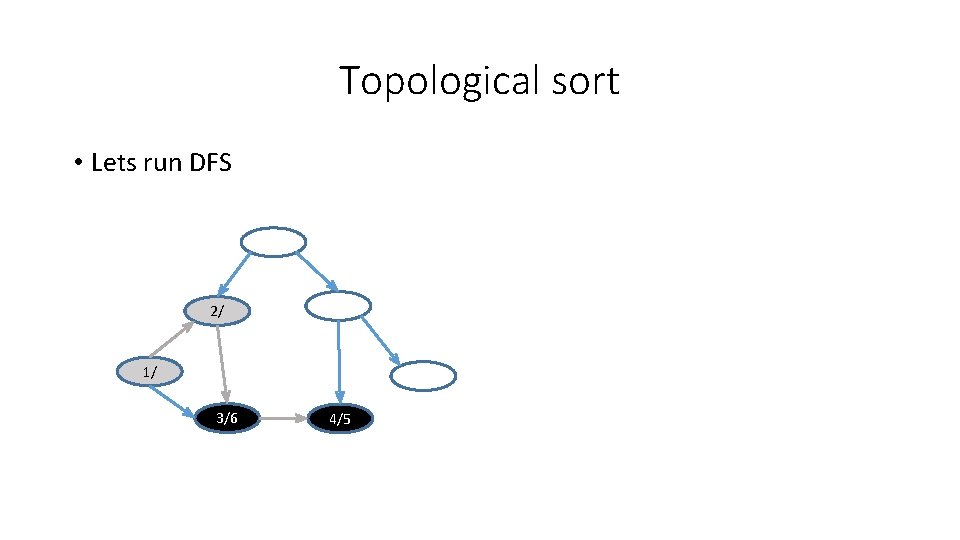
Topological sort • Lets run DFS 2/ 1/ 3/

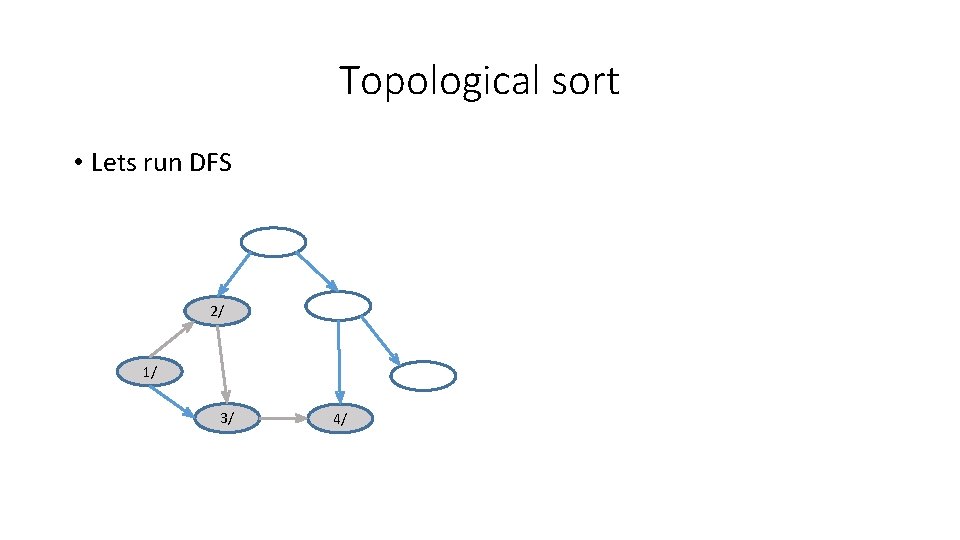
Topological sort • Lets run DFS 2/ 1/ 3/ 4/

Topological sort • Lets run DFS 2/ 1/ 3/ 4/5

Topological sort • Lets run DFS 2/ 1/ 3/6 4/5

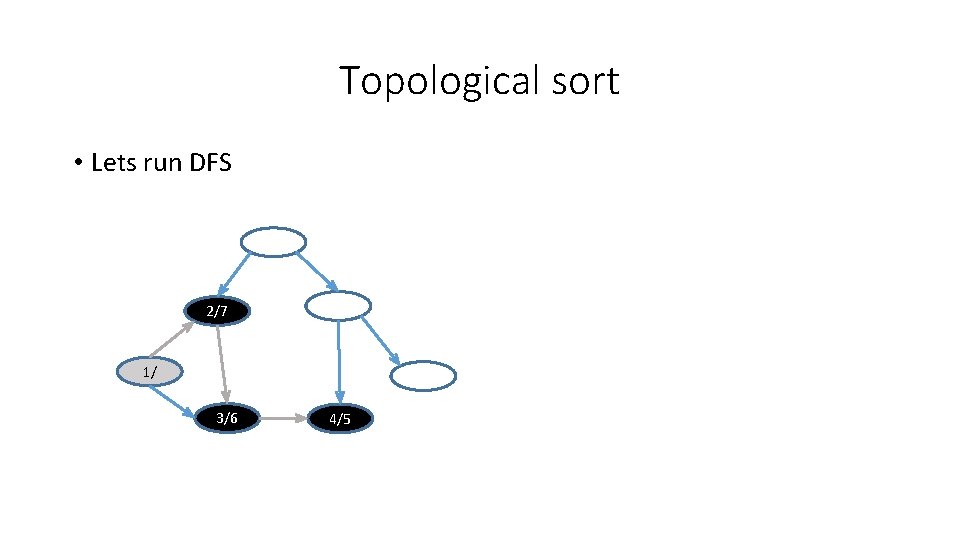
Topological sort • Lets run DFS 2/7 1/ 3/6 4/5

Topological sort • Lets run DFS 2/7 1/ 3/6 4/5

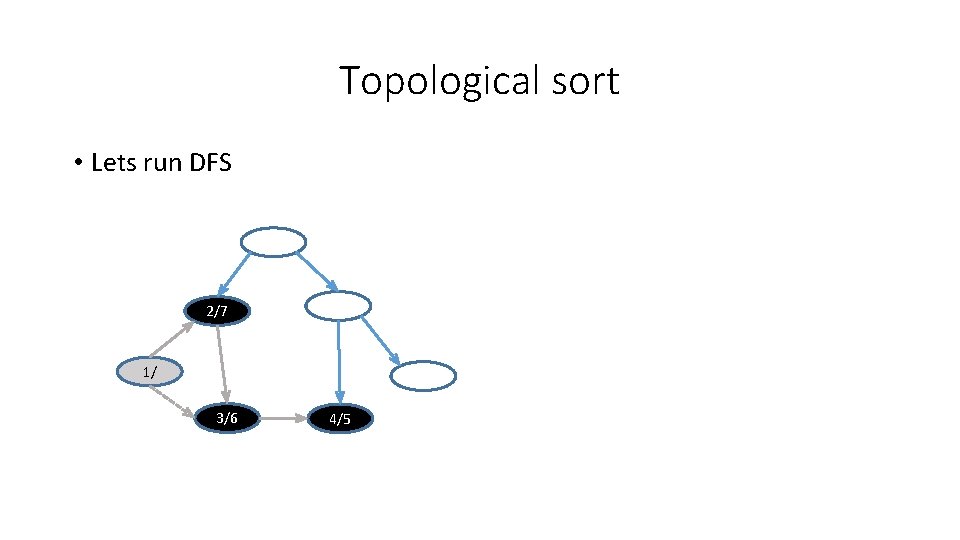
Topological sort • Lets run DFS 2/7 1/8 3/6 4/5

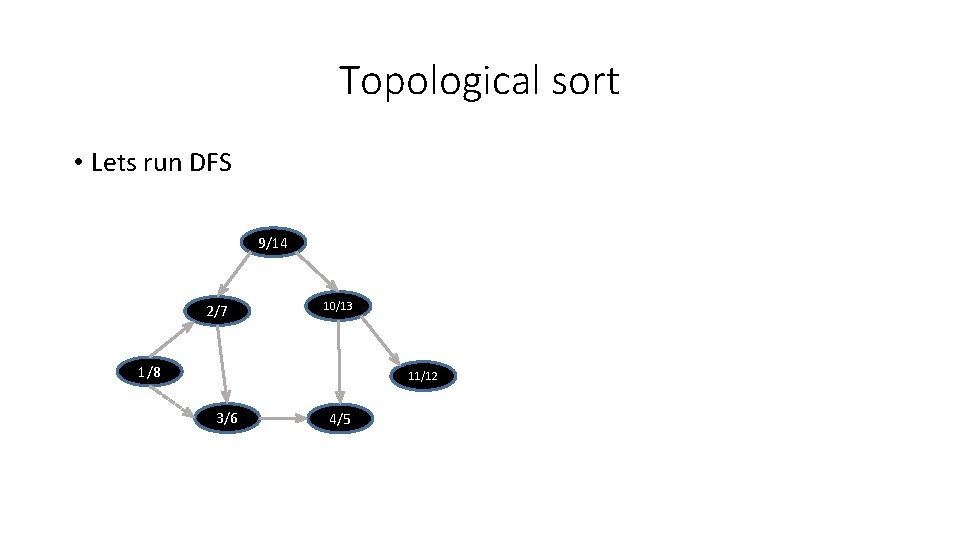
Topological sort • Lets run DFS 9/14 2/7 10/13 1/8 11/12 3/6 4/5

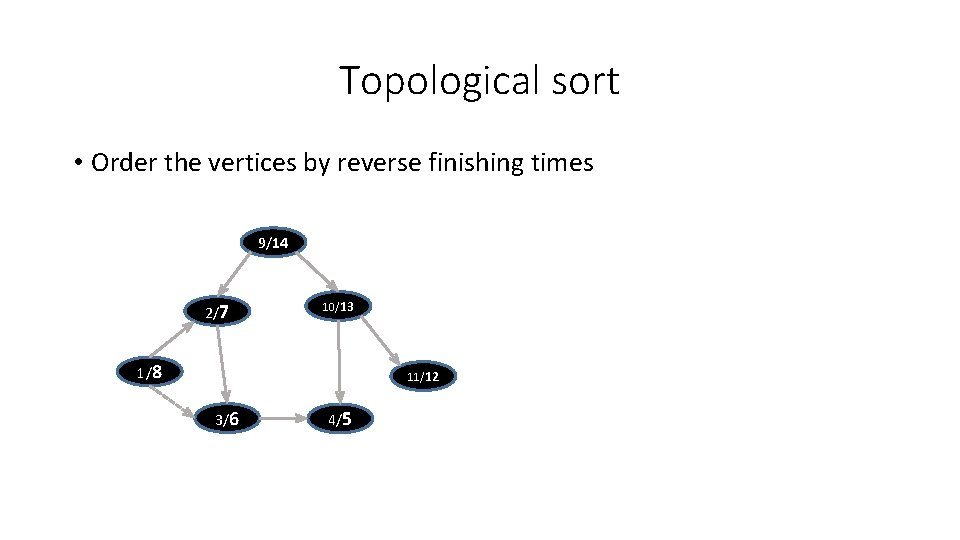
Topological sort • Order the vertices by reverse finishing times 9/14 2/7 10/13 1/8 11/12 3/6 4/5

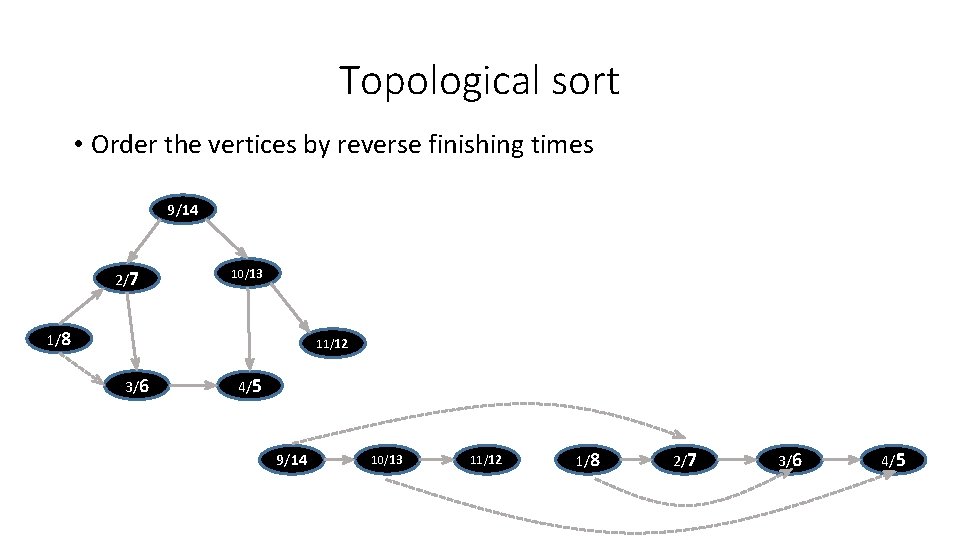
Topological sort • Order the vertices by reverse finishing times 9/14 2/7 10/13 1/8 11/12 3/6 4/5 9/14 10/13 11/12 1/8 2/7 3/6 4/5

Topological sort (correctness) Thm 6: DFS on DAG does not produce back edges

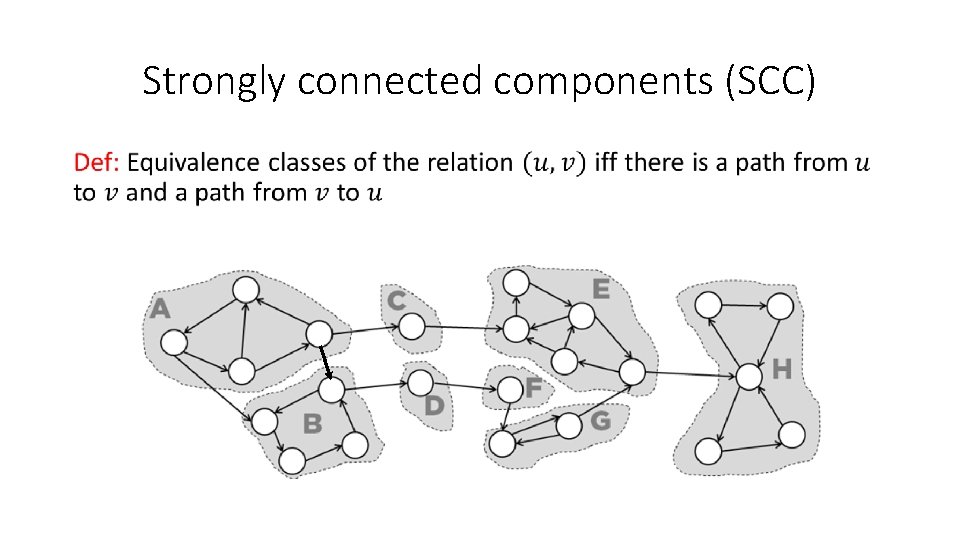
Strongly connected components (SCC) •




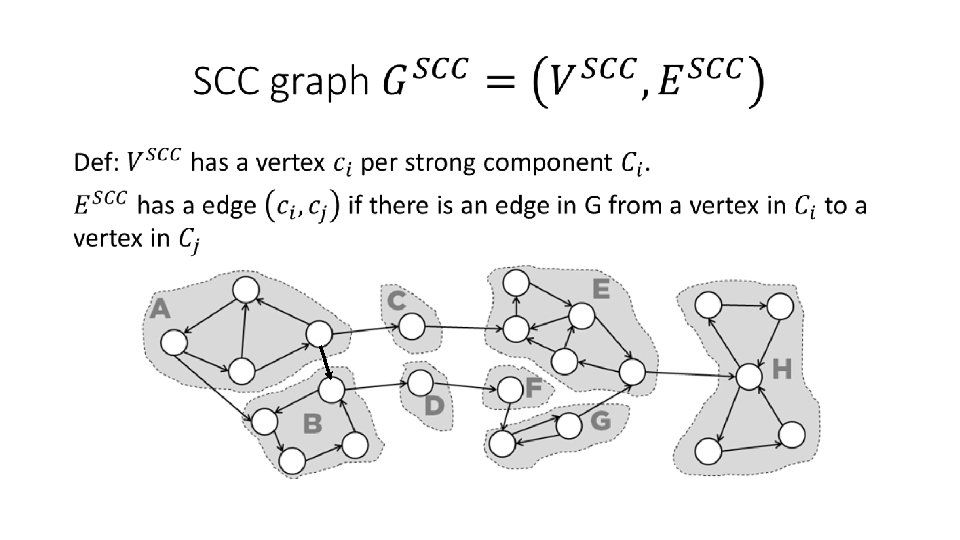
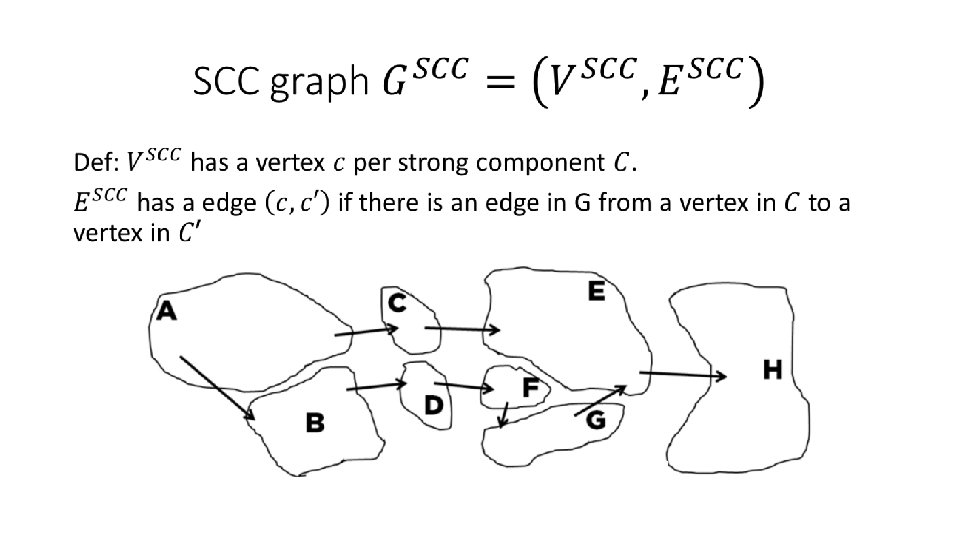
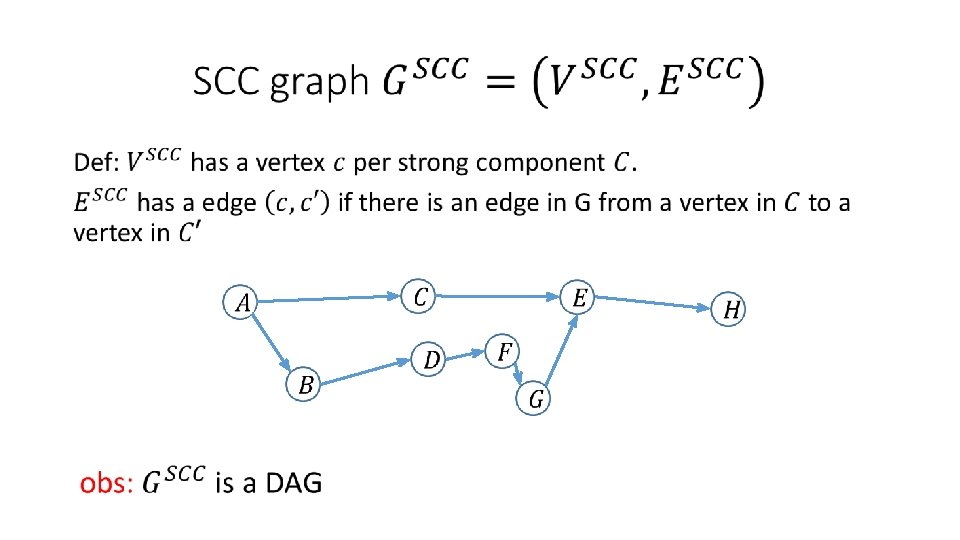
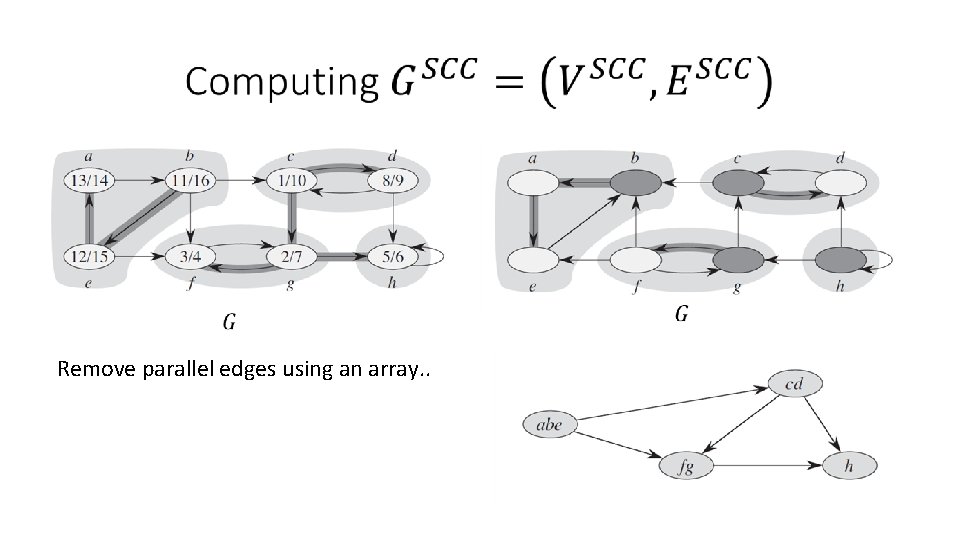
Computing strongly connected components

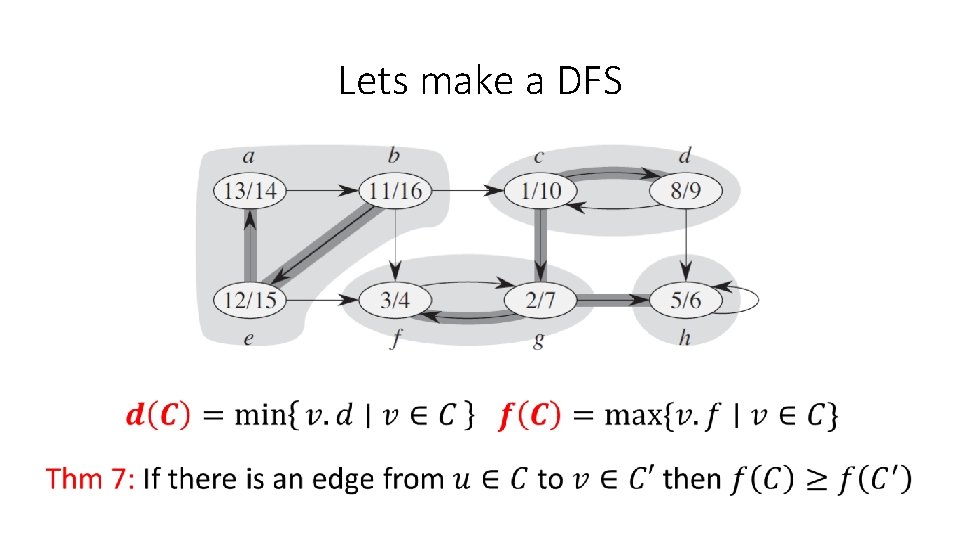
Lets make a DFS

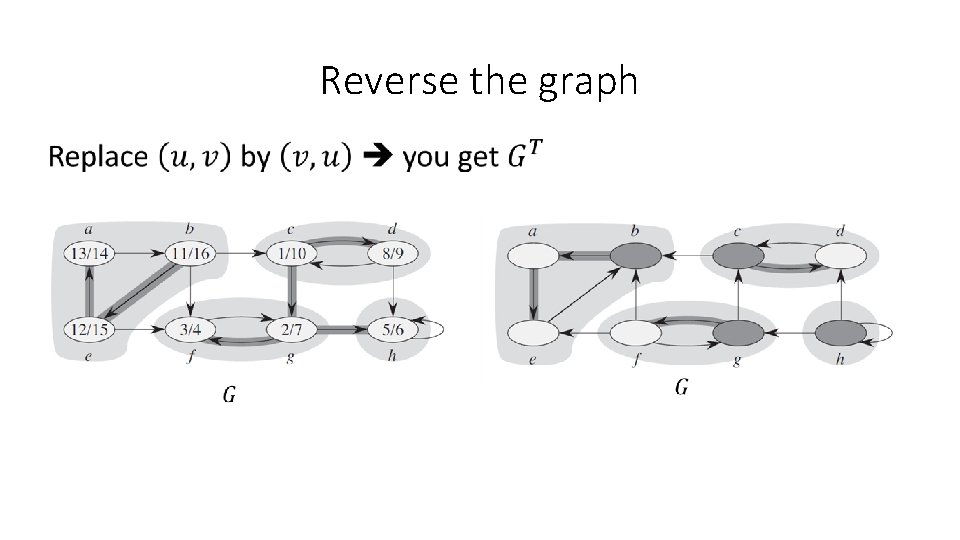
Reverse the graph

An algorithm to compute SCC’s

Remove parallel edges using an array. .

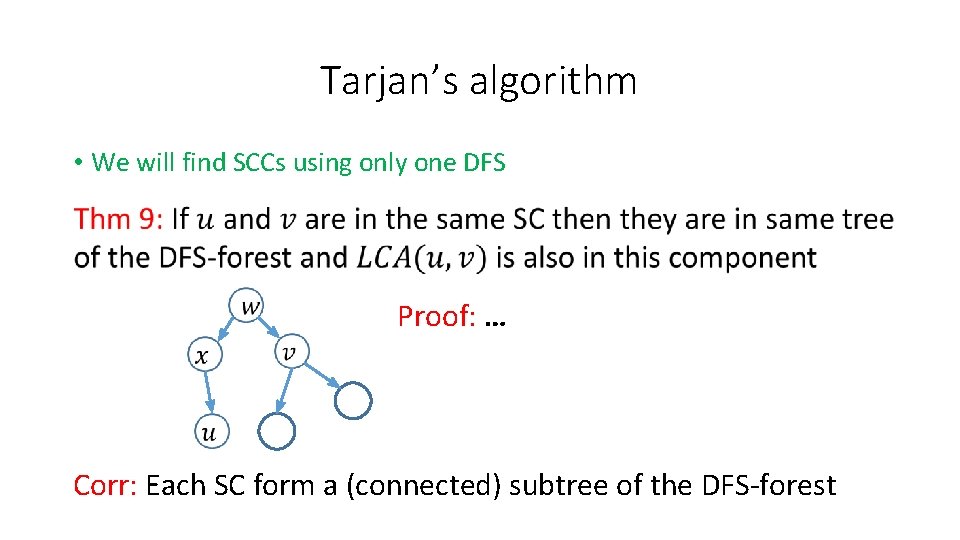
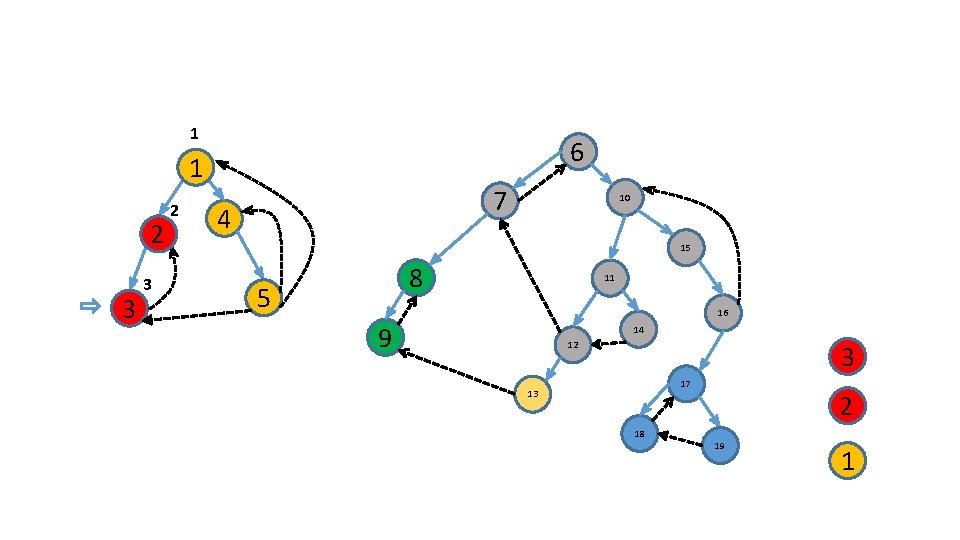
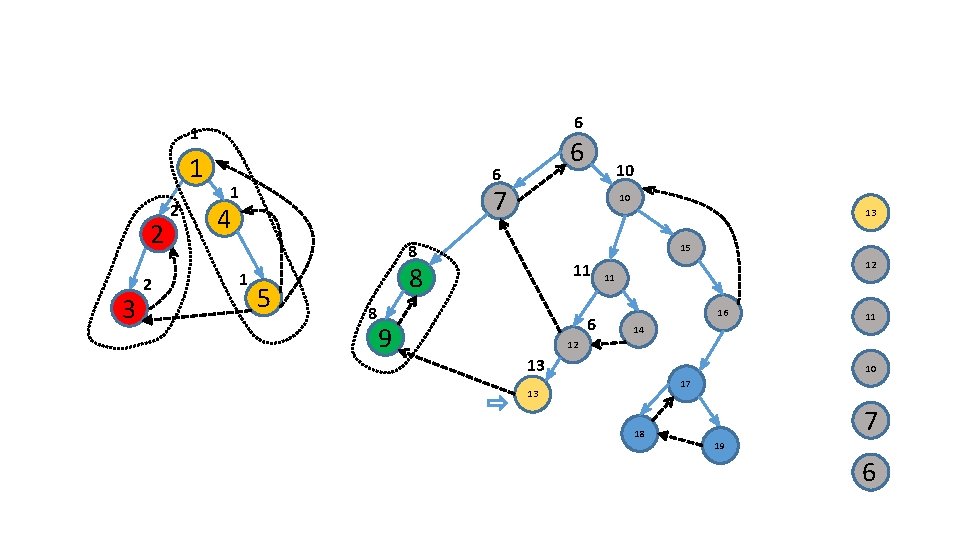
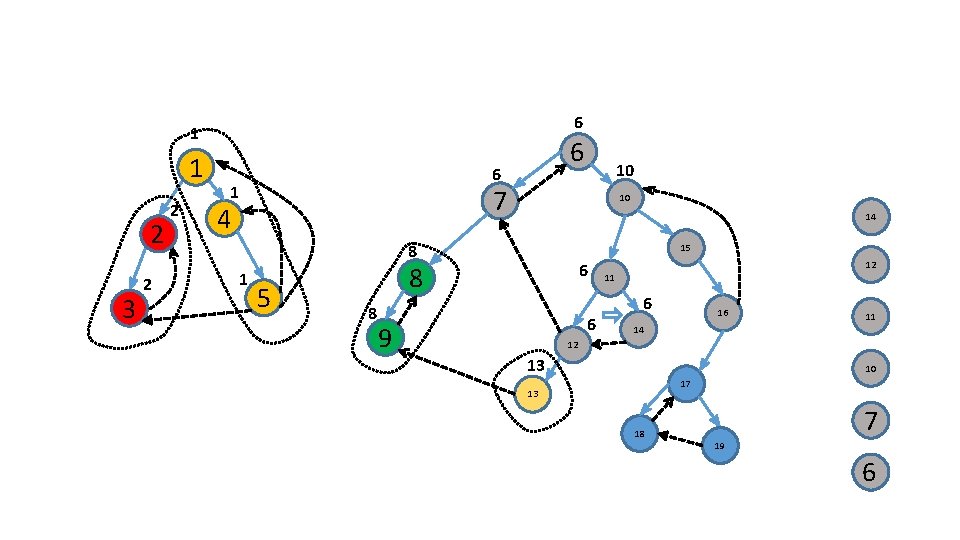
Tarjan’s algorithm • We will find SCCs using only one DFS Proof: … Corr: Each SC form a (connected) subtree of the DFS-forest

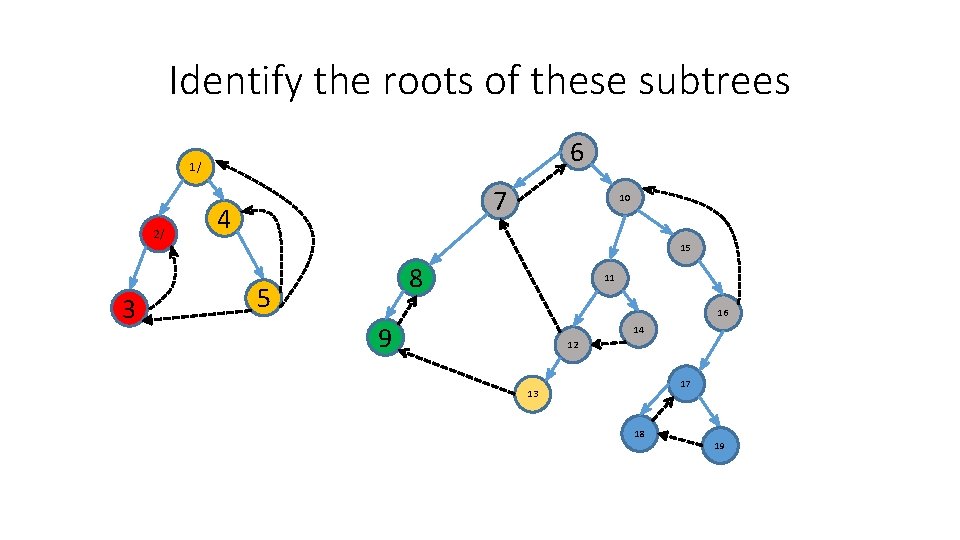
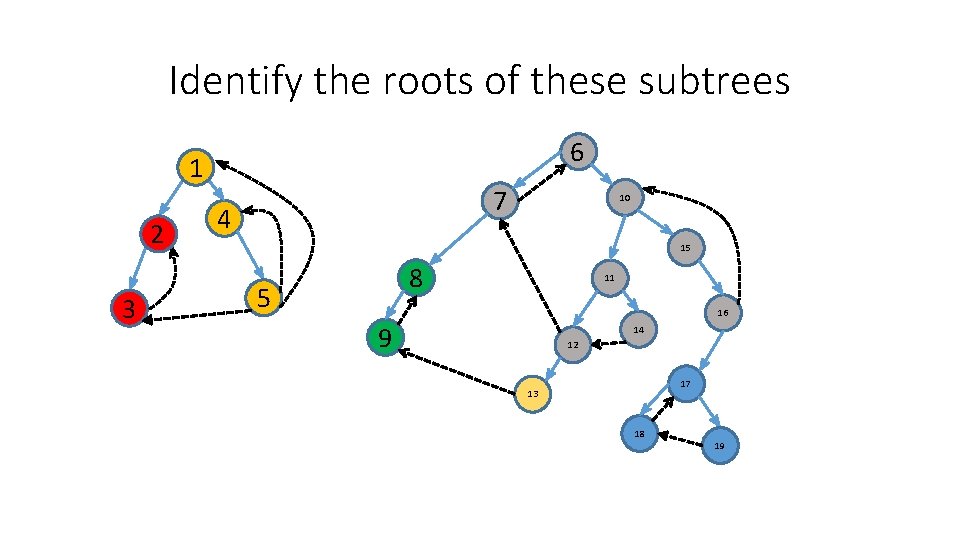
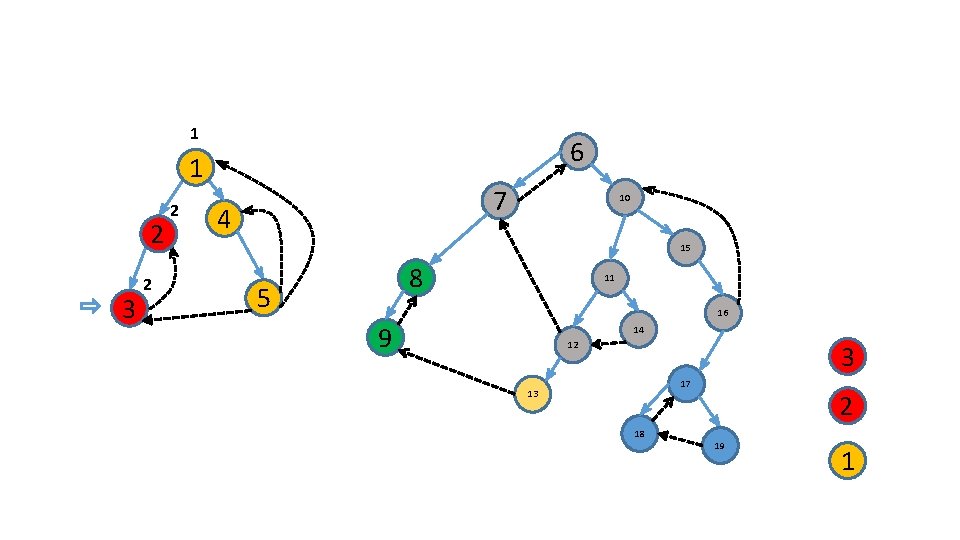
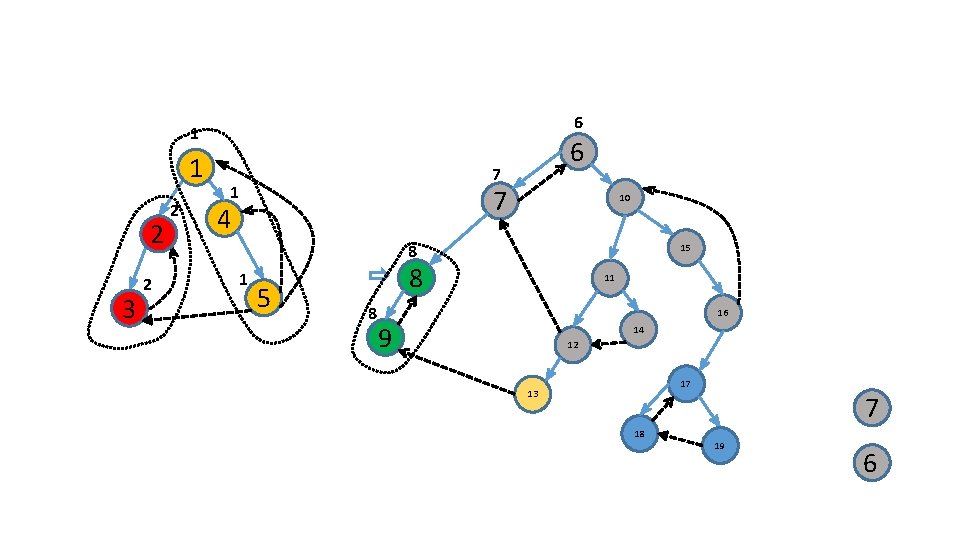
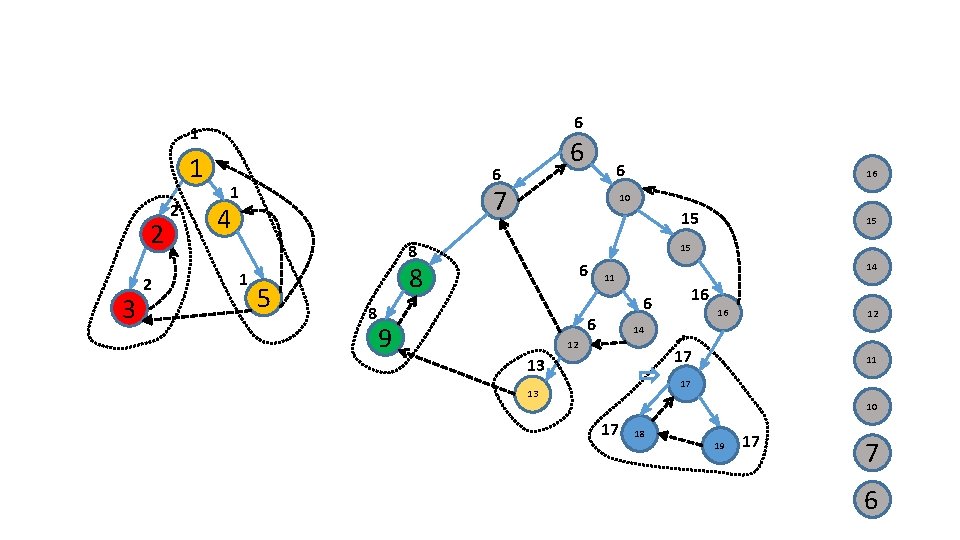
Identify the roots of these subtrees 6 1/ 2/ 7 4 10 15 3 8 5 11 16 9 14 12 17 13 18 19

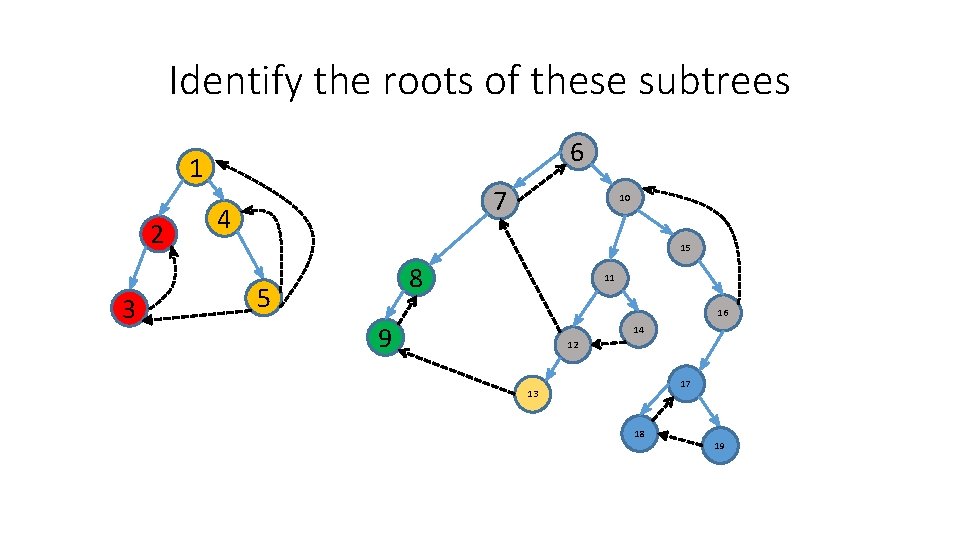
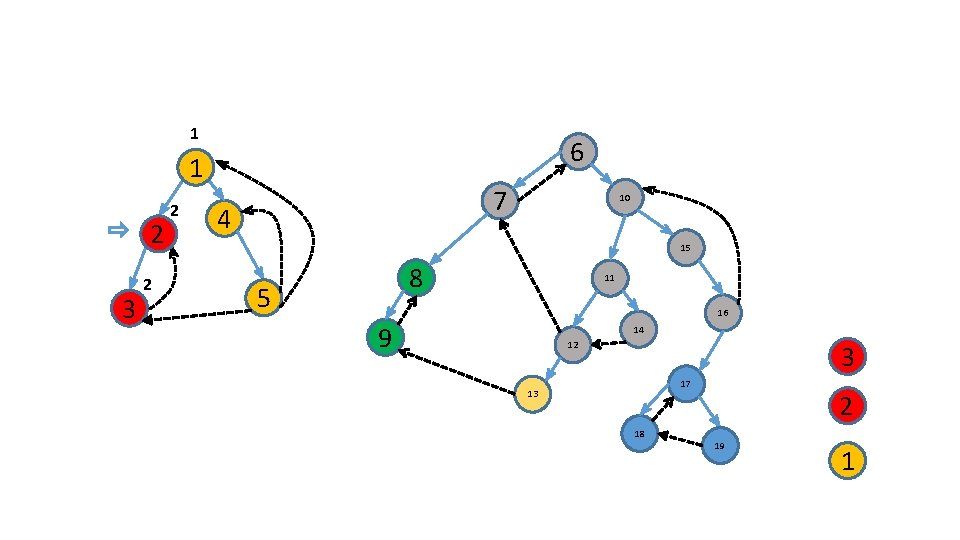
Identify the roots of these subtrees 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19

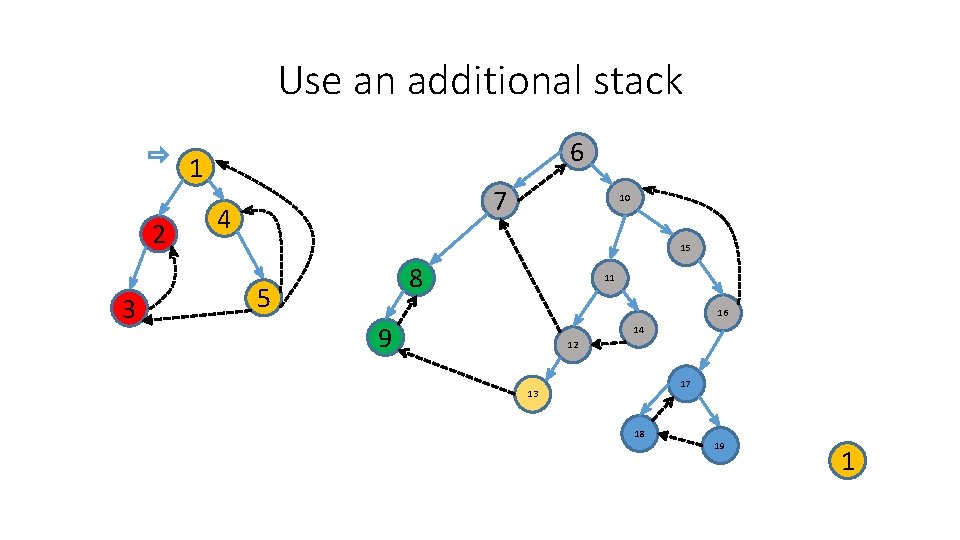
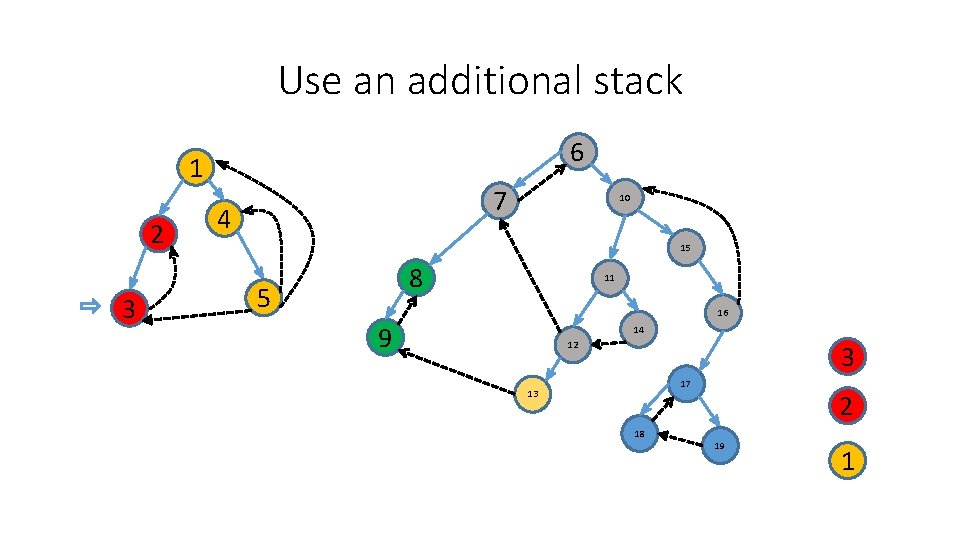
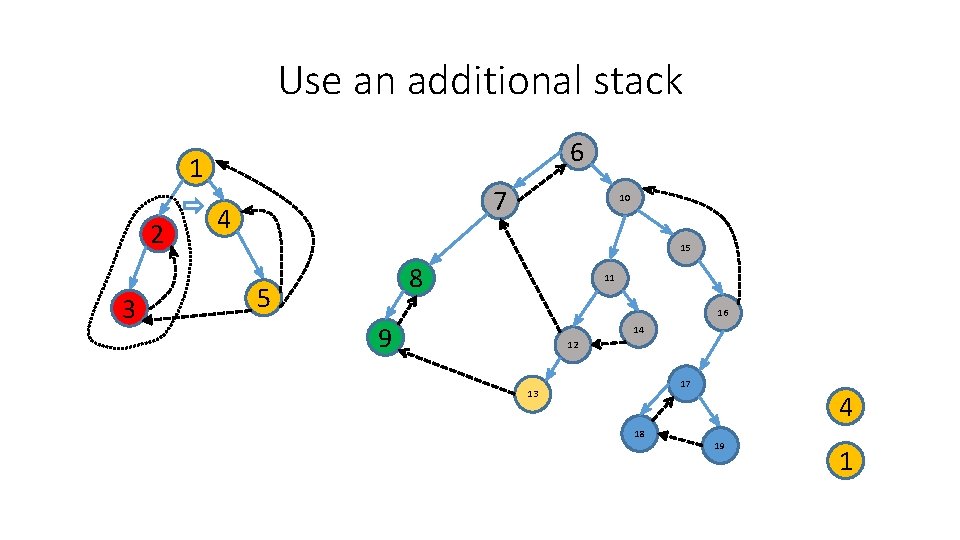
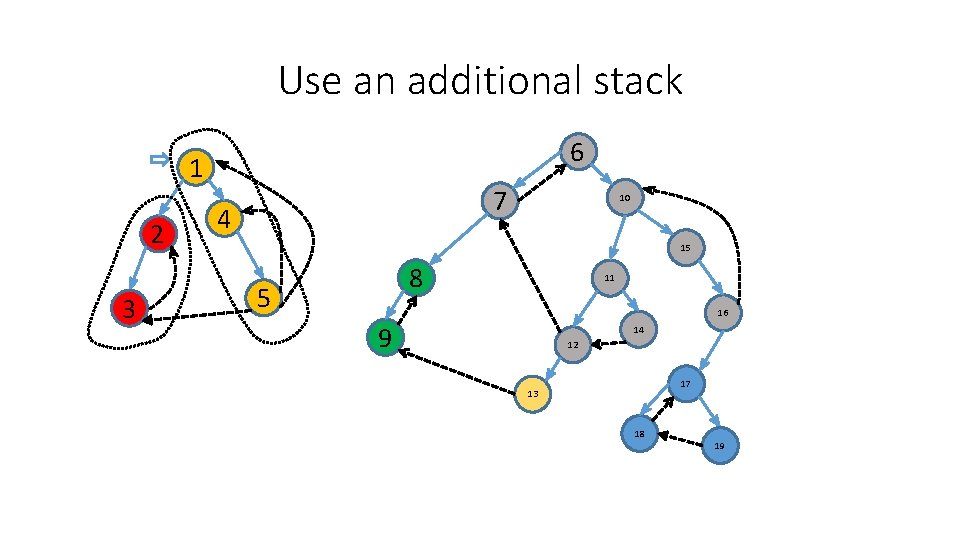
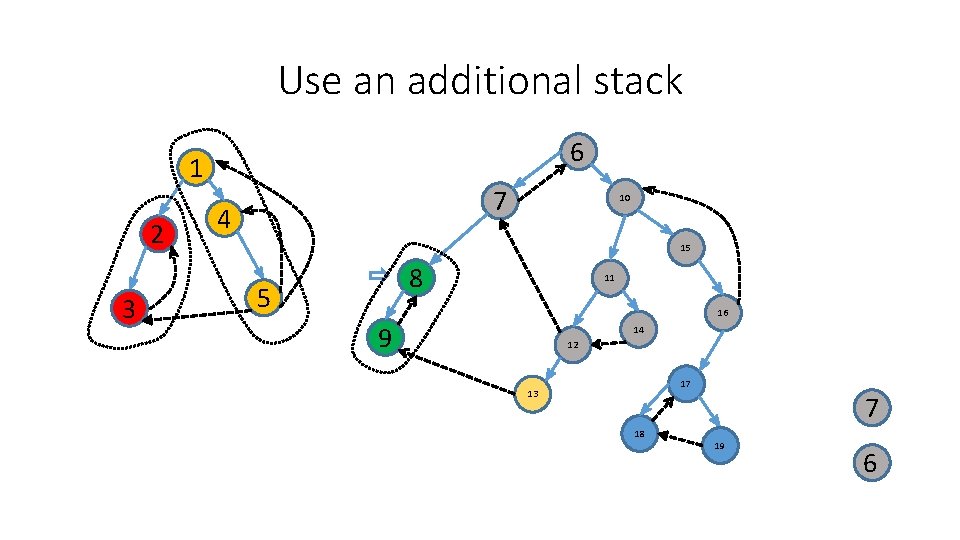
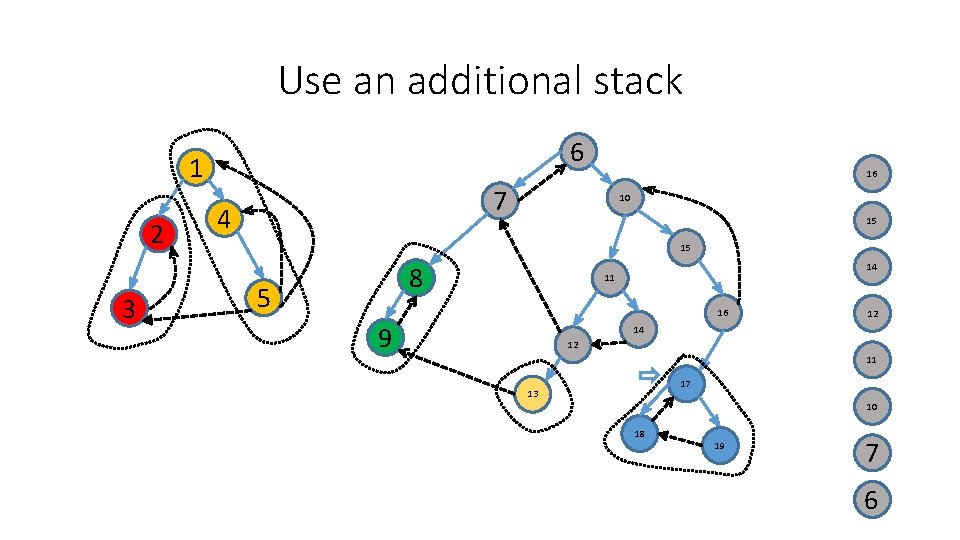
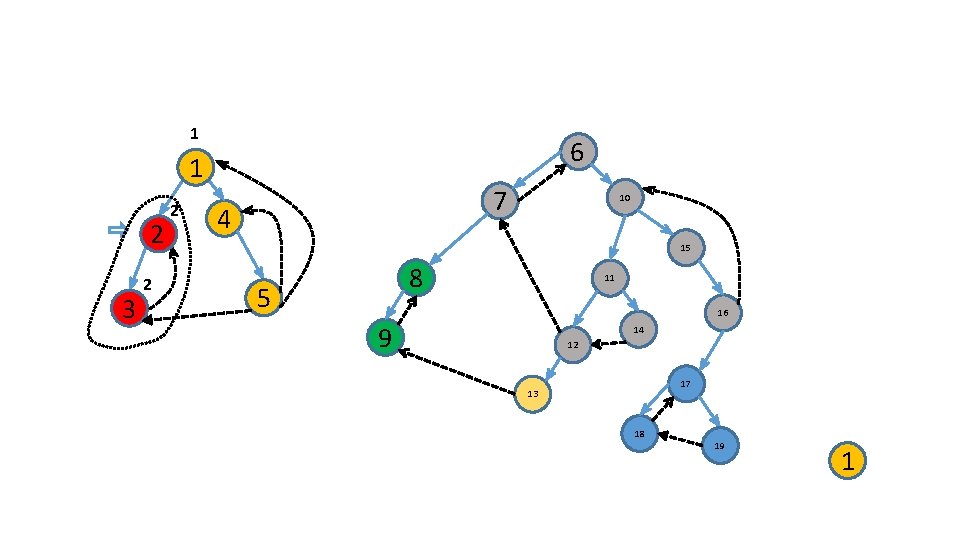
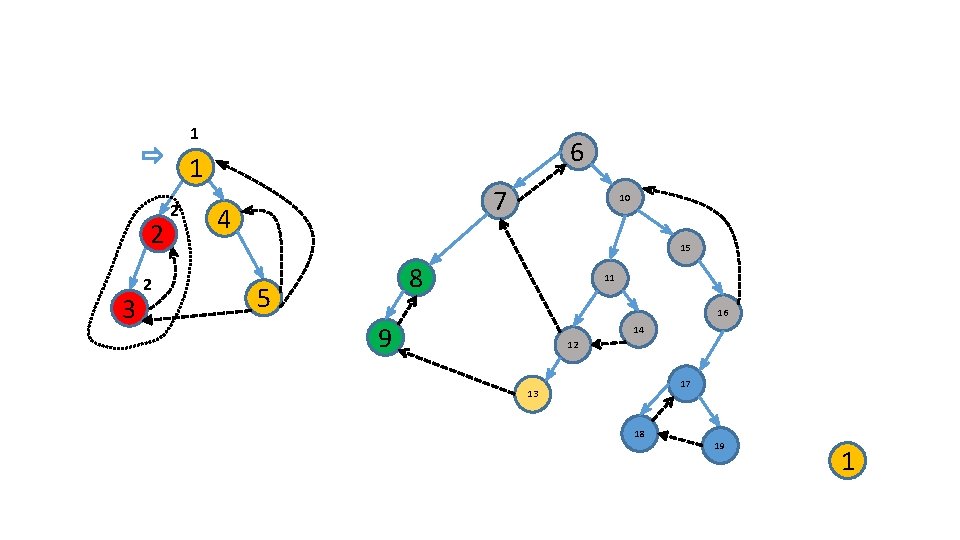
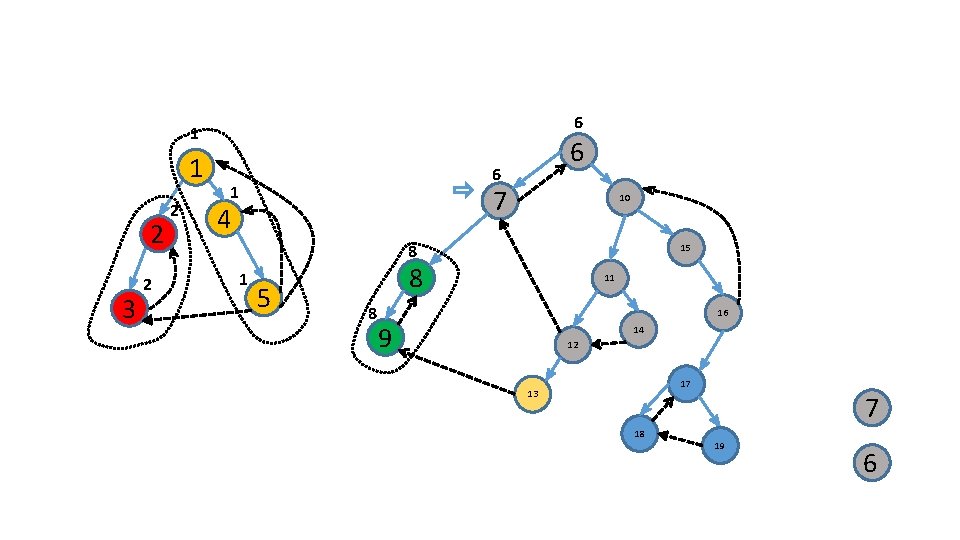
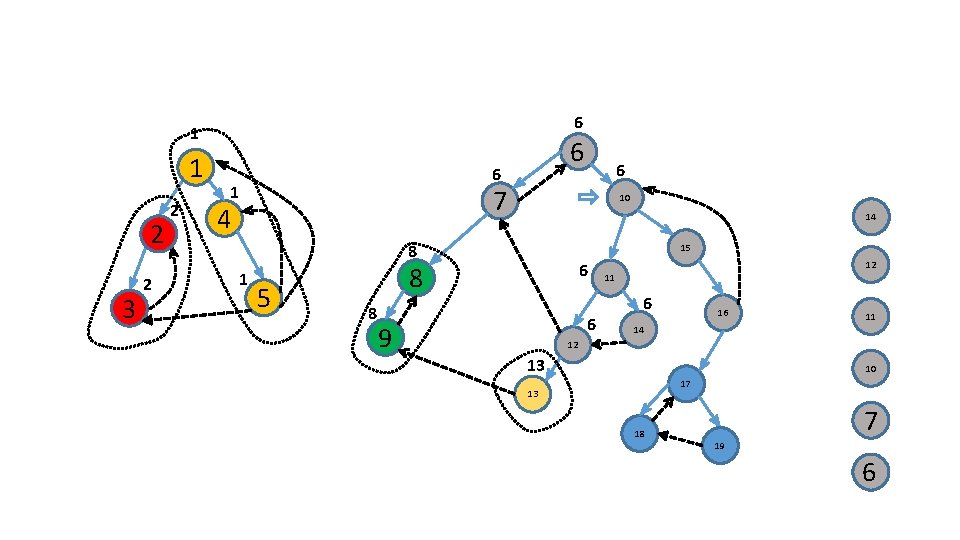
Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19 1

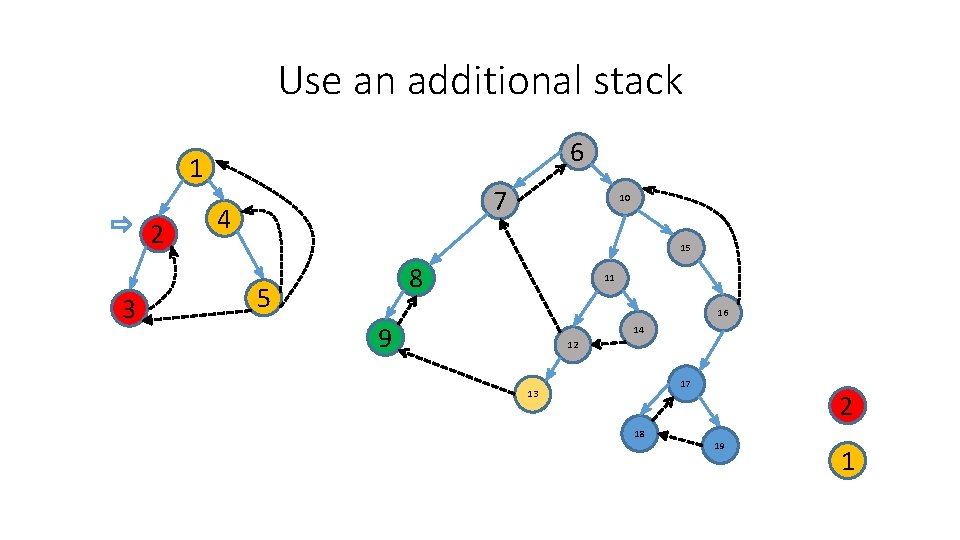
Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 2 19 1

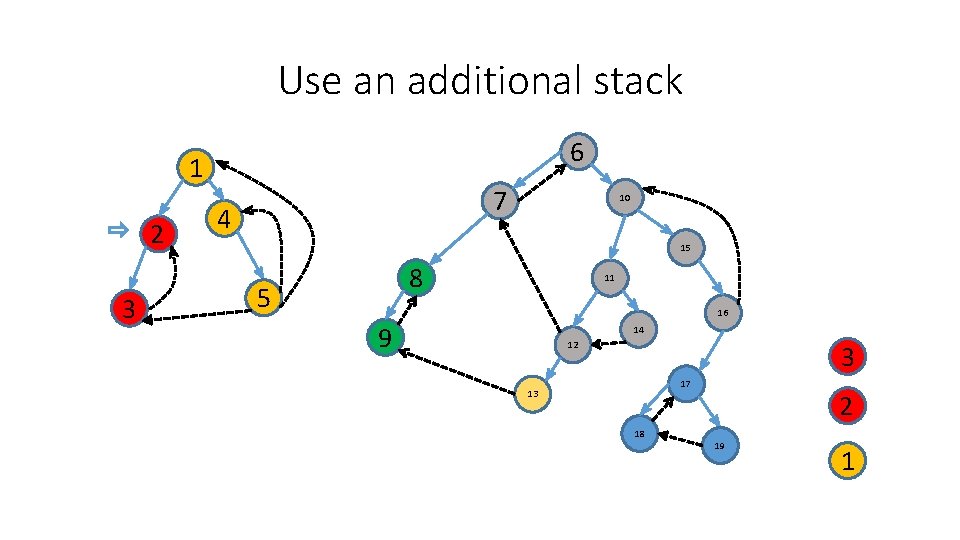
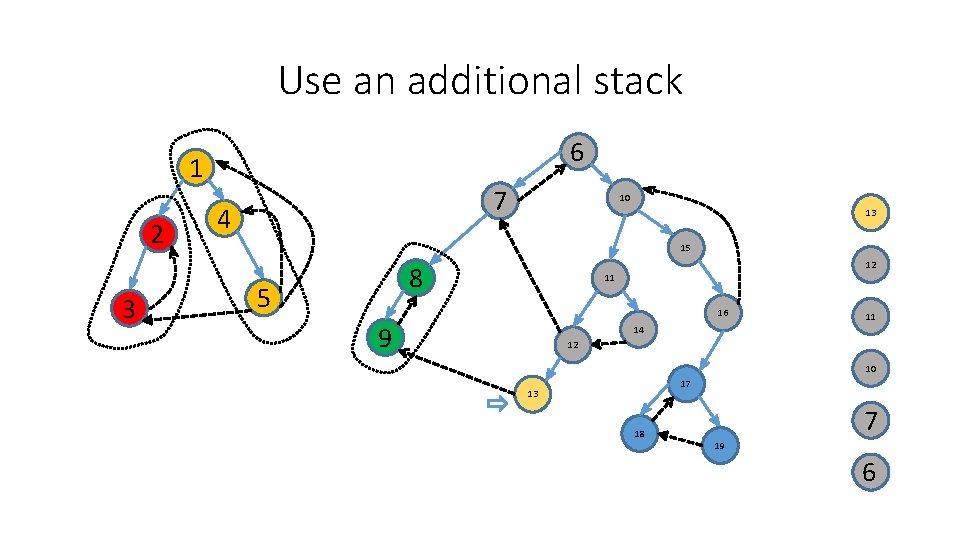
Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 3 17 13 18 2 19 1

Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 3 17 13 18 2 19 1

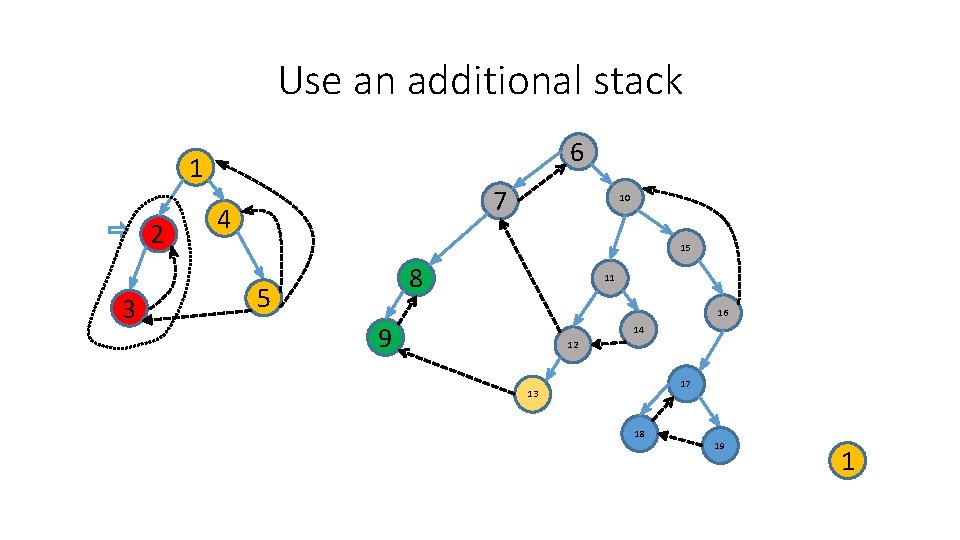
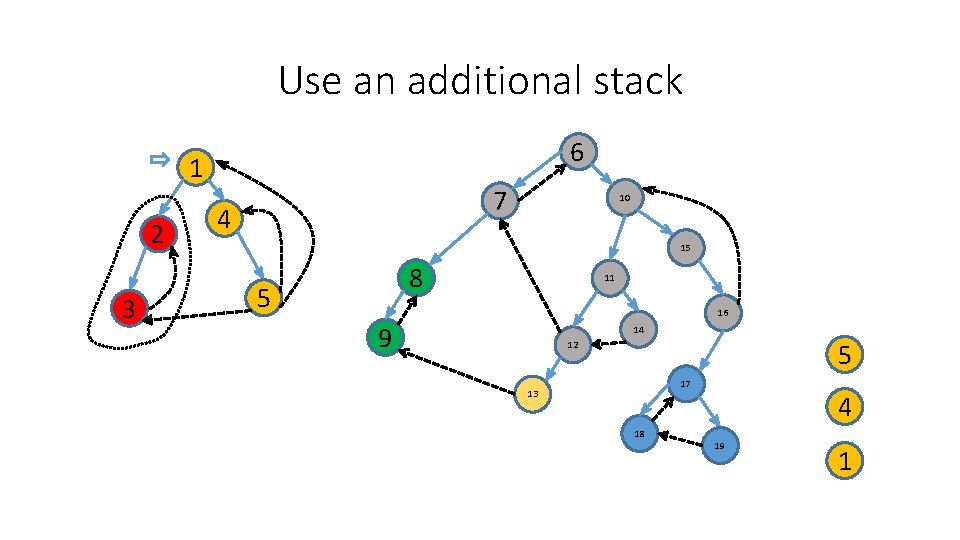
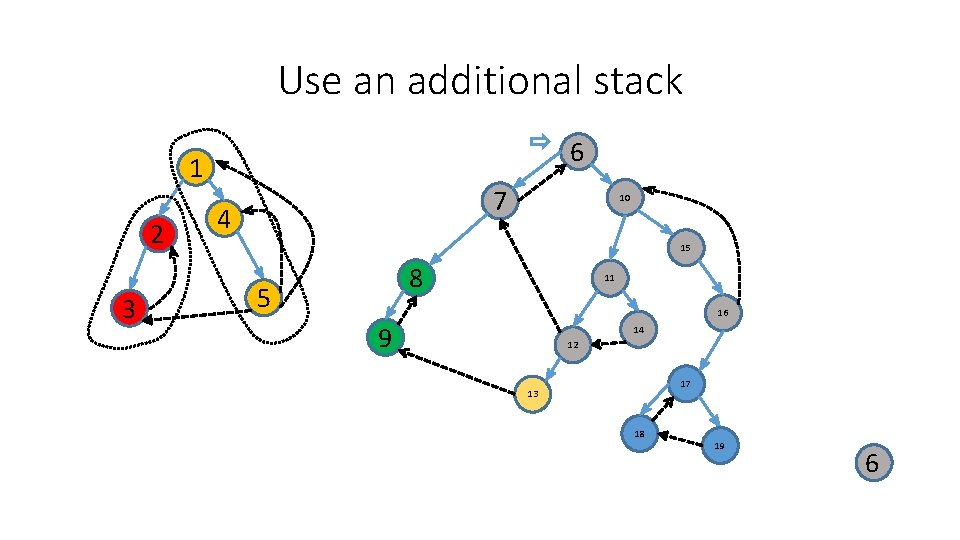
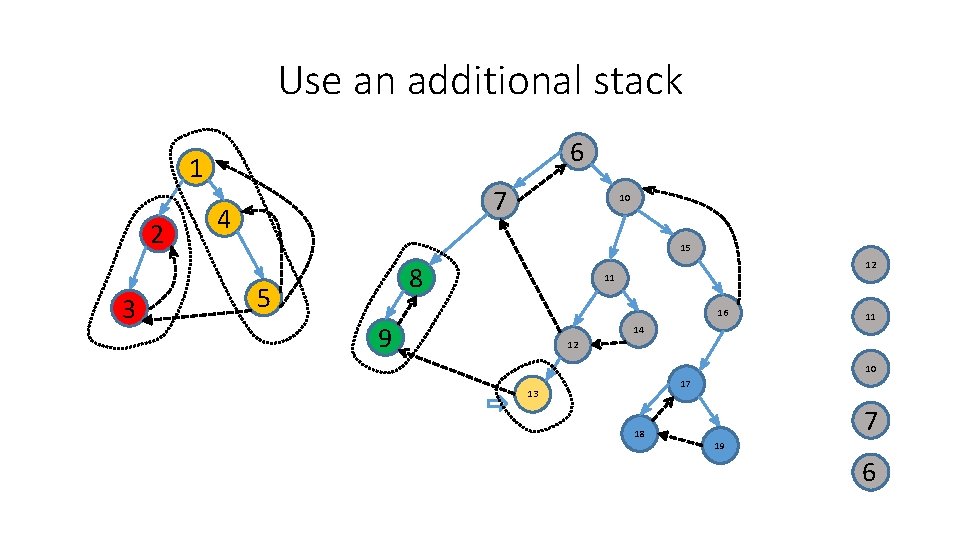
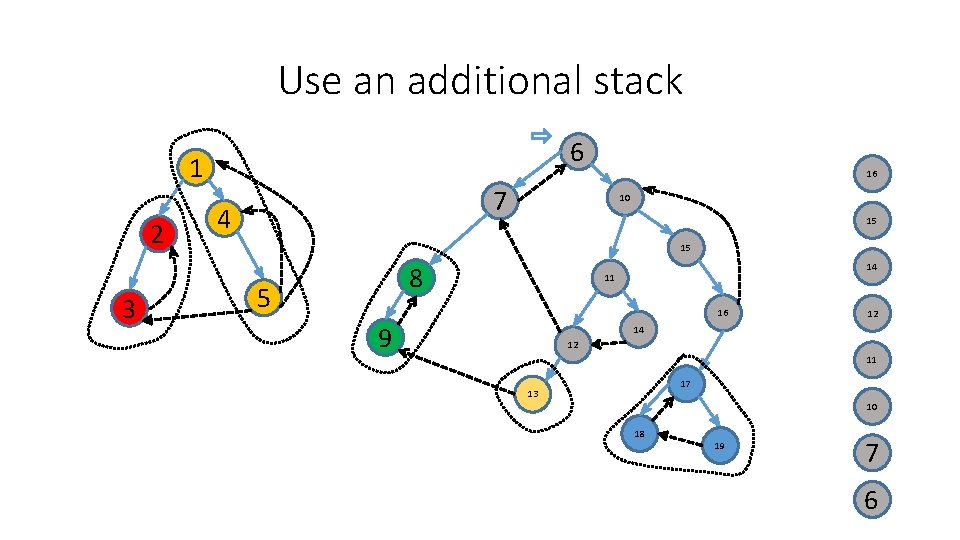
Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19 1

Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19 1

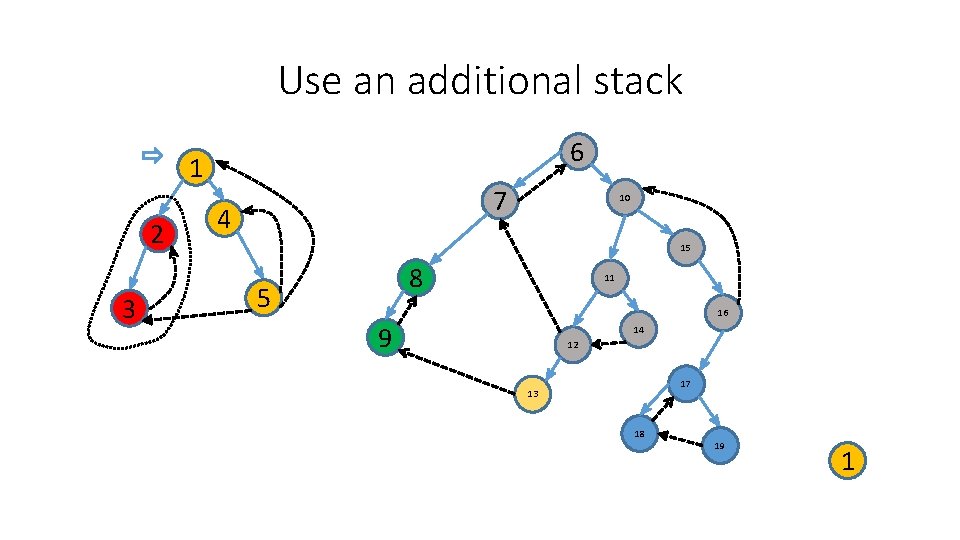
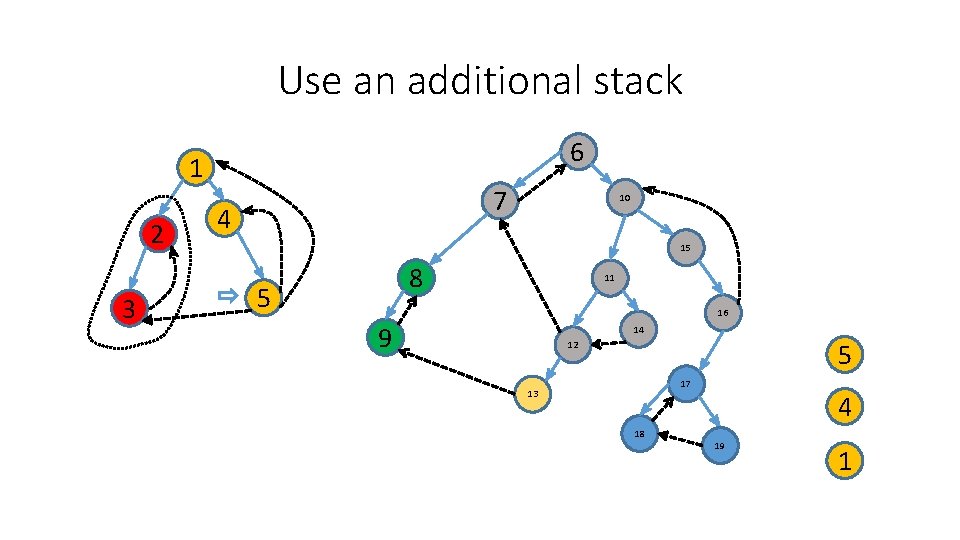
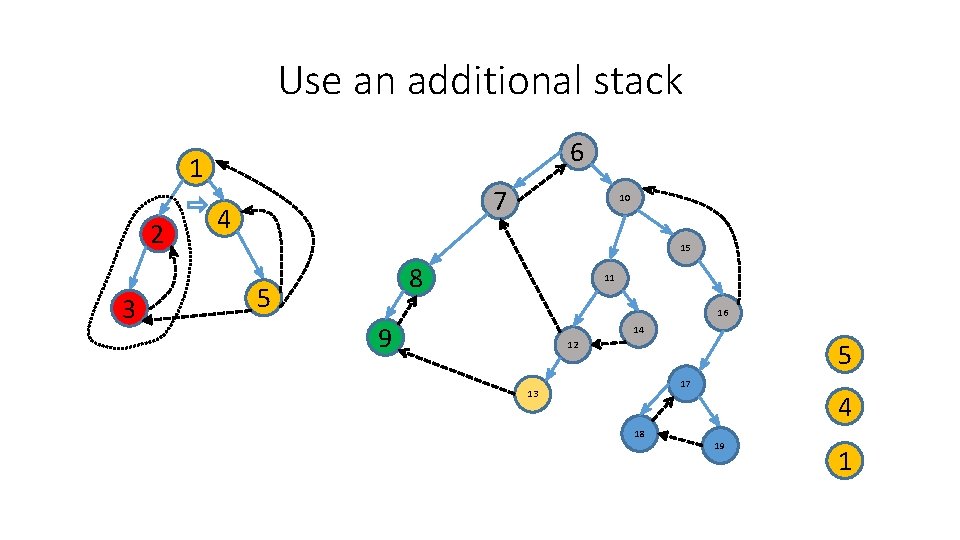
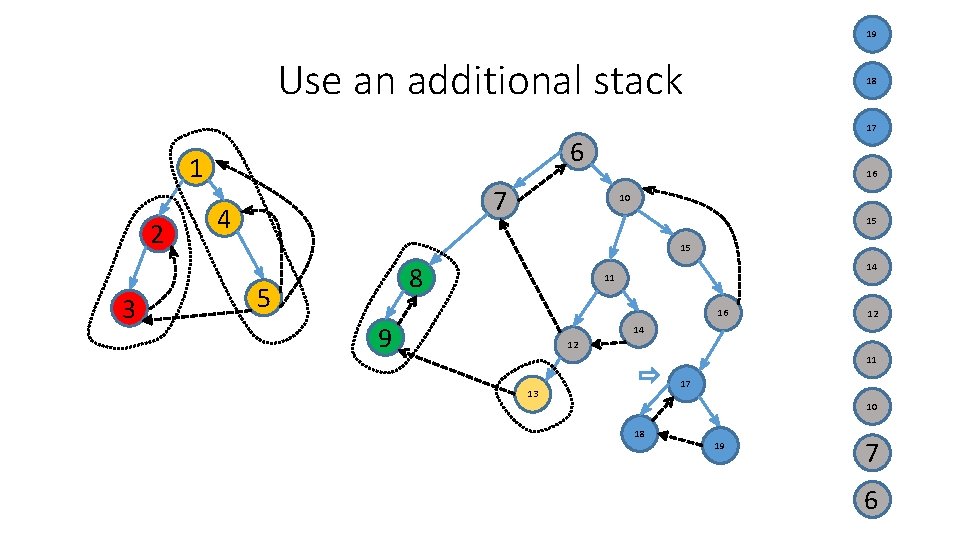
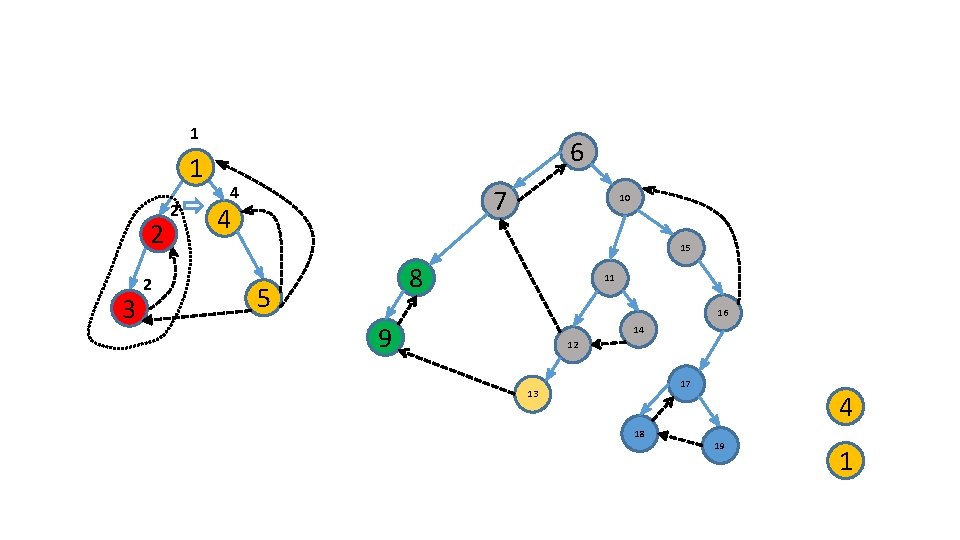
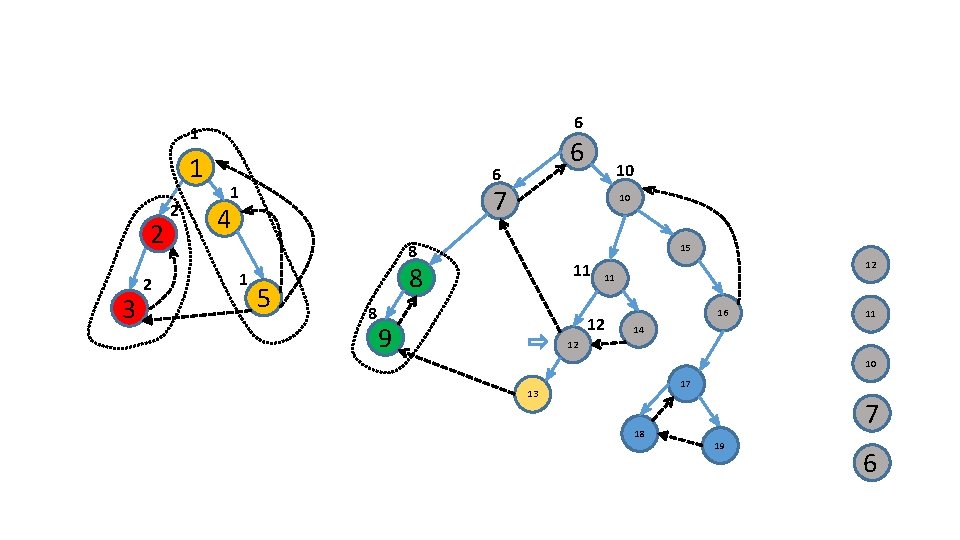
Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 4 19 1

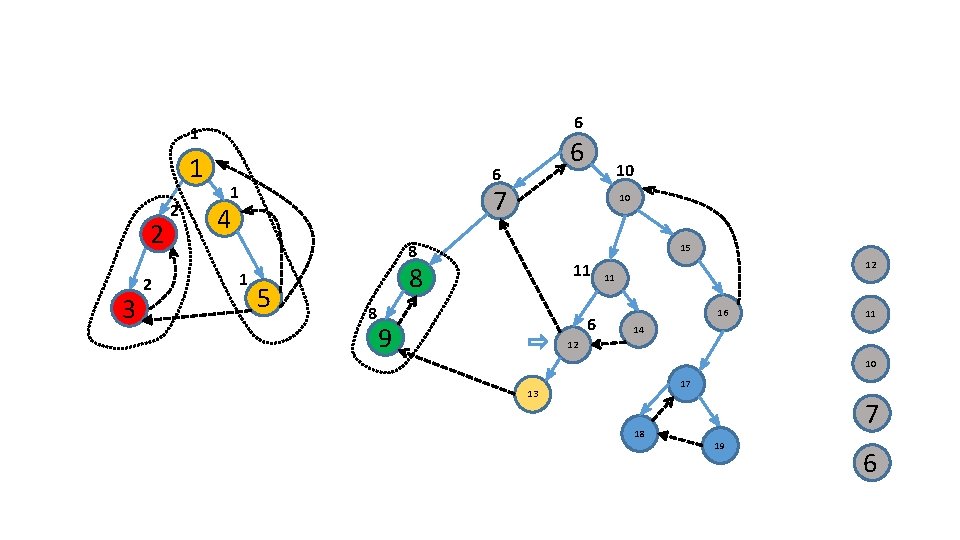
Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 5 12 17 13 18 4 19 1

Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 5 12 17 13 18 4 19 1

Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 5 12 17 13 18 4 19 1

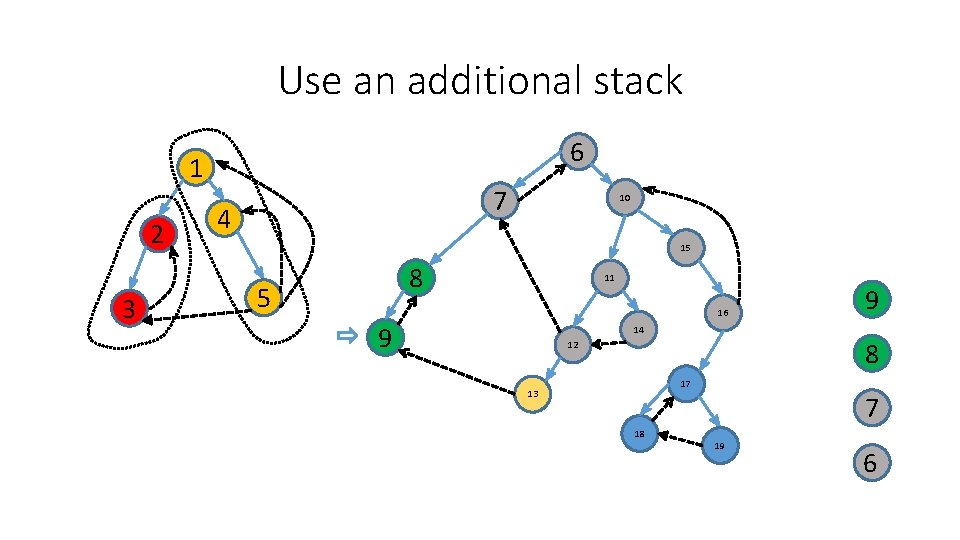
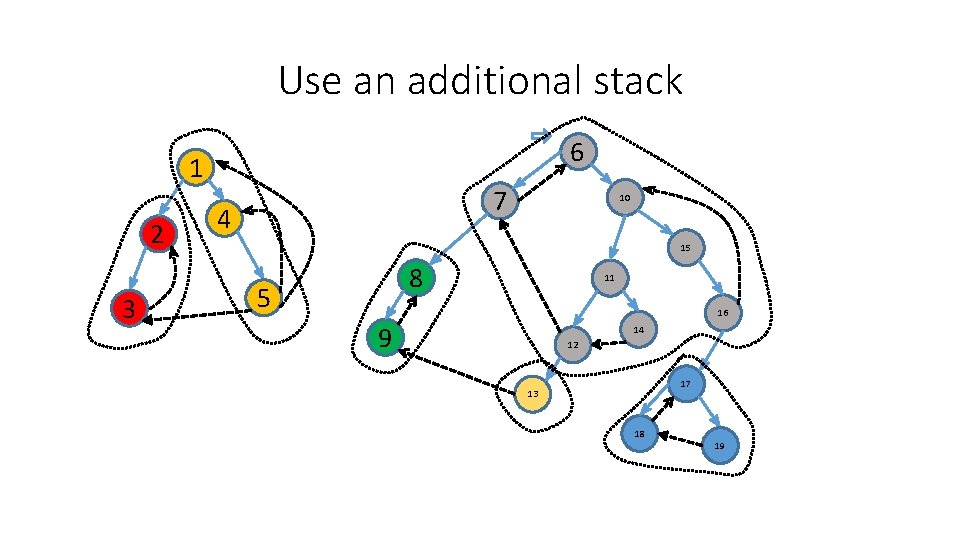
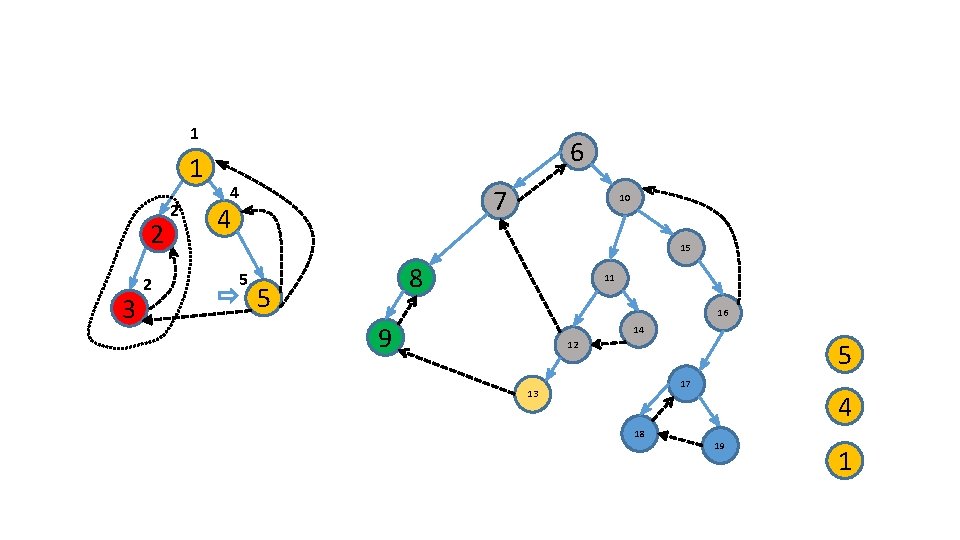
Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19

Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19 6

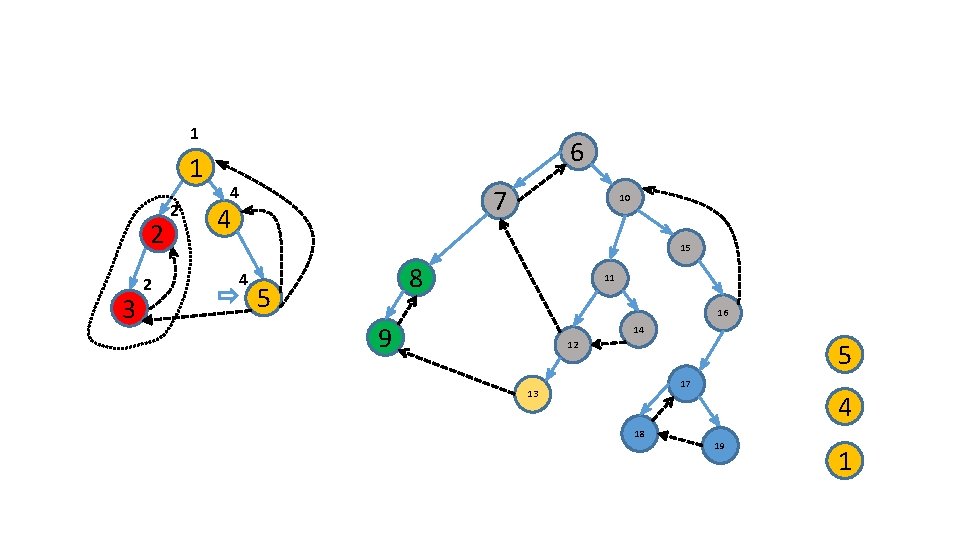
Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 9 14 8 12 17 13 7 18 19 6

Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 9 14 8 12 17 13 7 18 19 6

Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 7 18 19 6

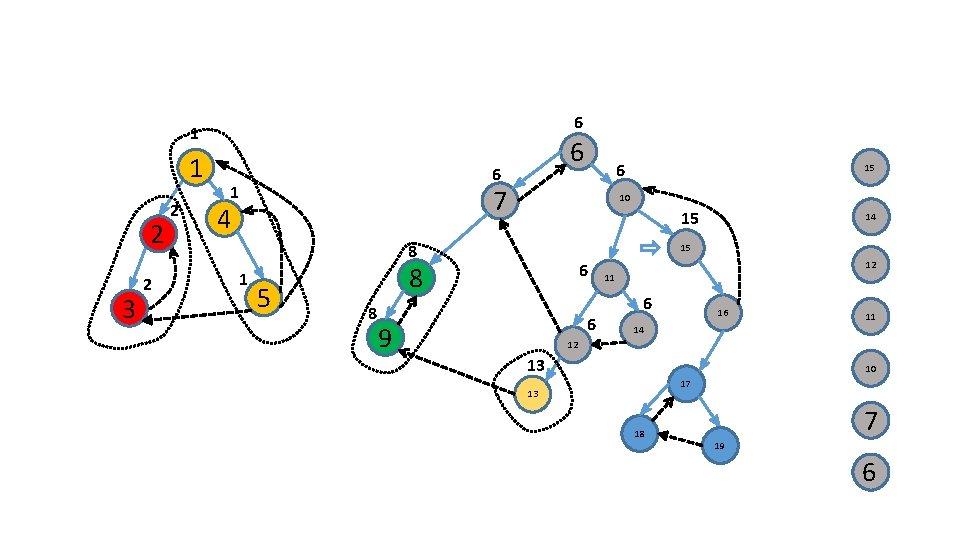
Use an additional stack 6 1 2 3 7 4 10 13 15 12 8 5 11 16 9 11 14 12 10 17 13 18 7 19 6

Use an additional stack 6 1 2 3 7 4 10 15 12 8 5 11 16 9 11 14 12 10 17 13 18 7 19 6

19 Use an additional stack 18 17 6 1 2 3 16 7 4 10 15 15 8 5 14 11 16 9 12 14 12 11 17 13 10 18 19 7 6

Use an additional stack 6 1 2 3 16 7 4 10 15 15 8 5 14 11 16 9 12 14 12 11 17 13 10 18 19 7 6

Use an additional stack 6 1 2 3 16 7 4 10 15 15 8 5 14 11 16 9 12 14 12 11 17 13 10 18 19 7 6

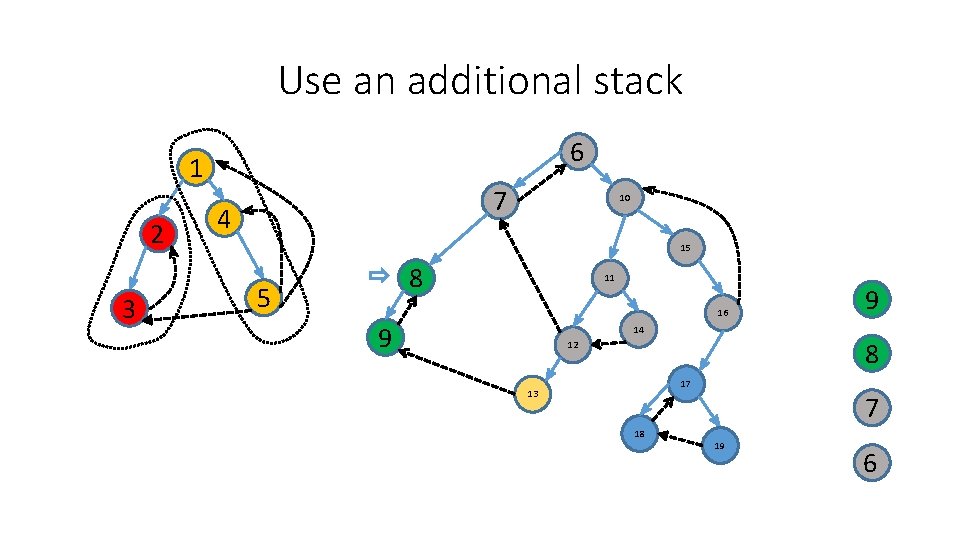
Use an additional stack 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19

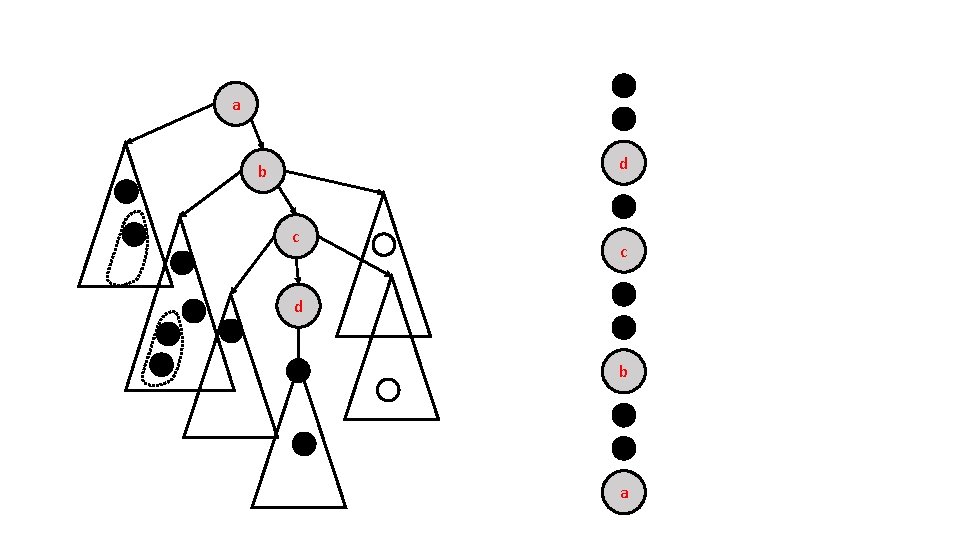
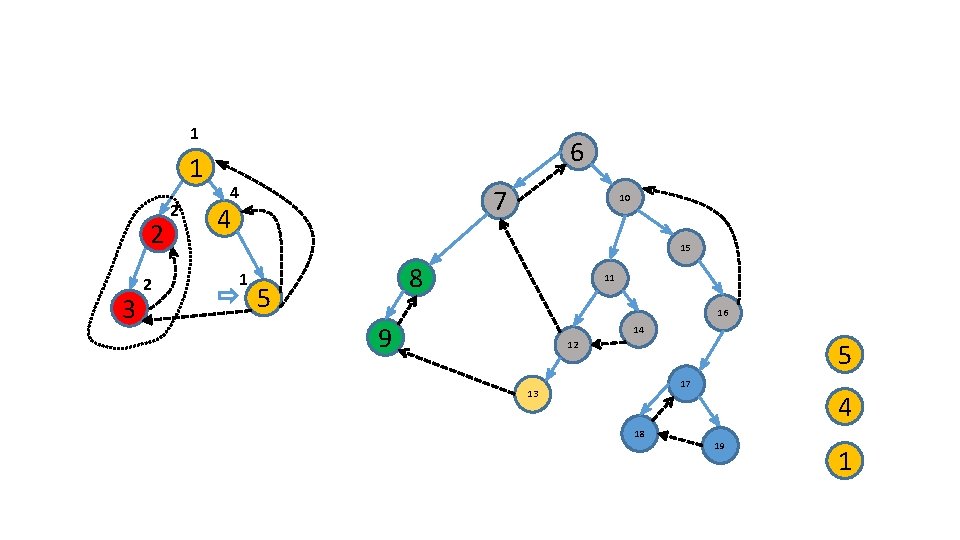
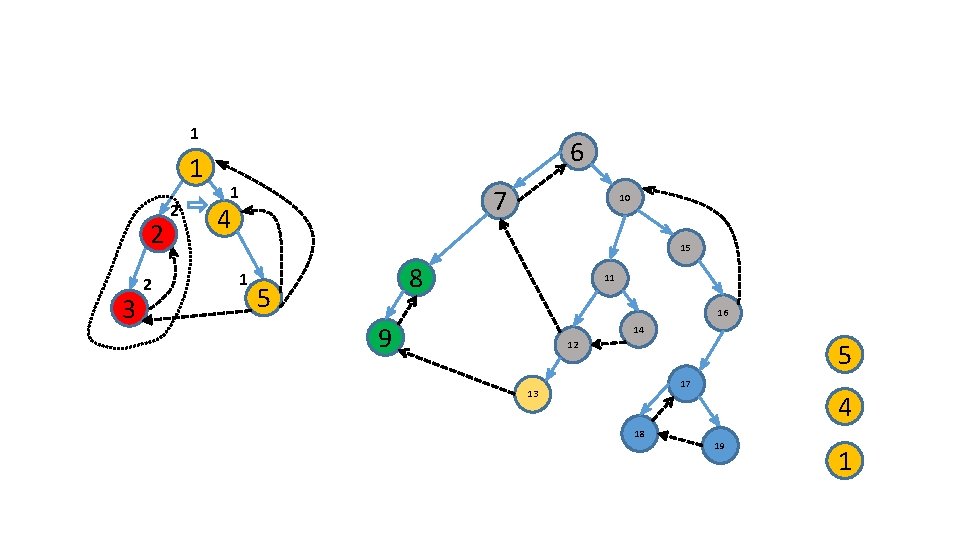
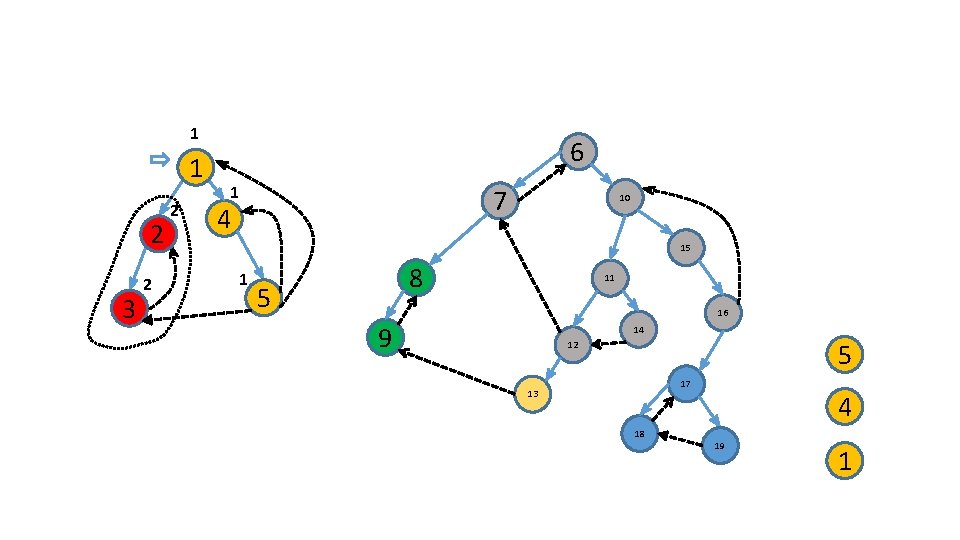
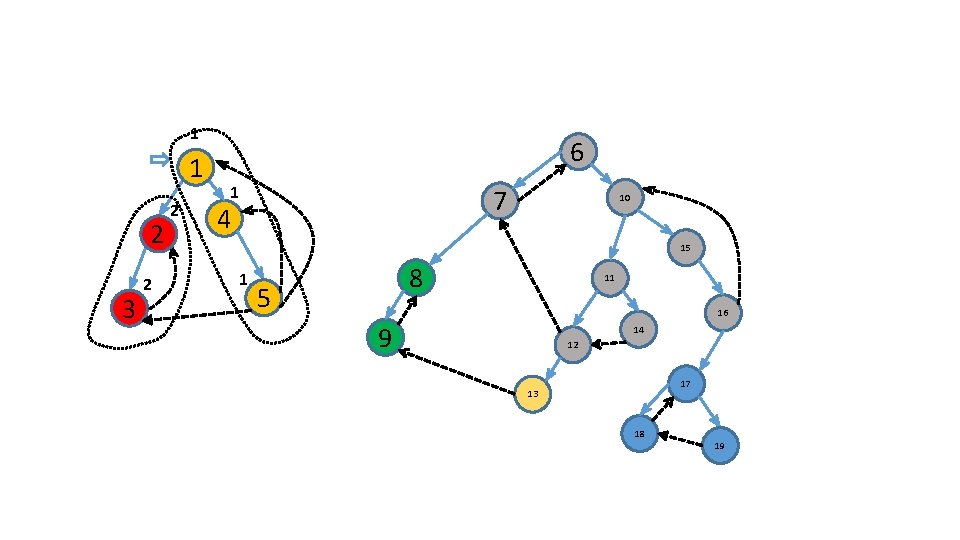
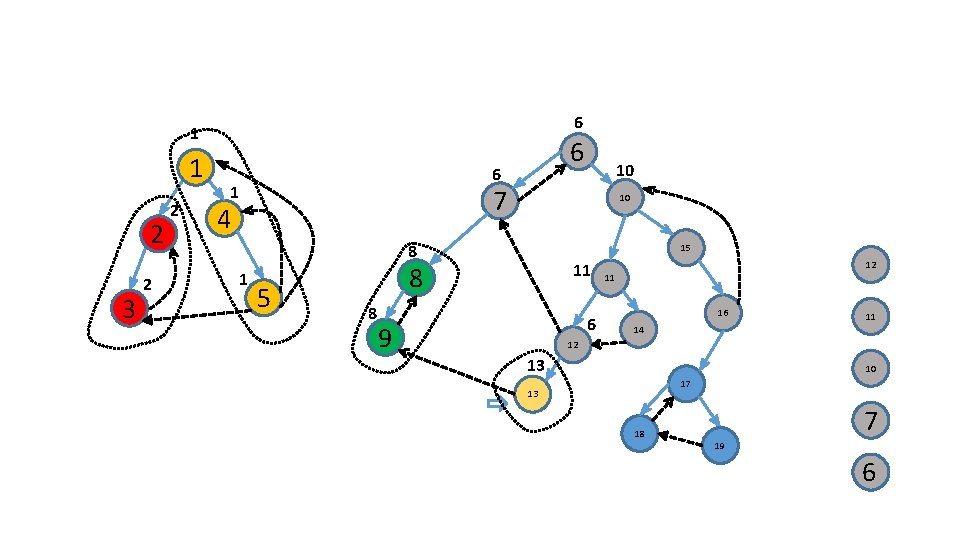
Characterize these roots ?

a d b c c d b a

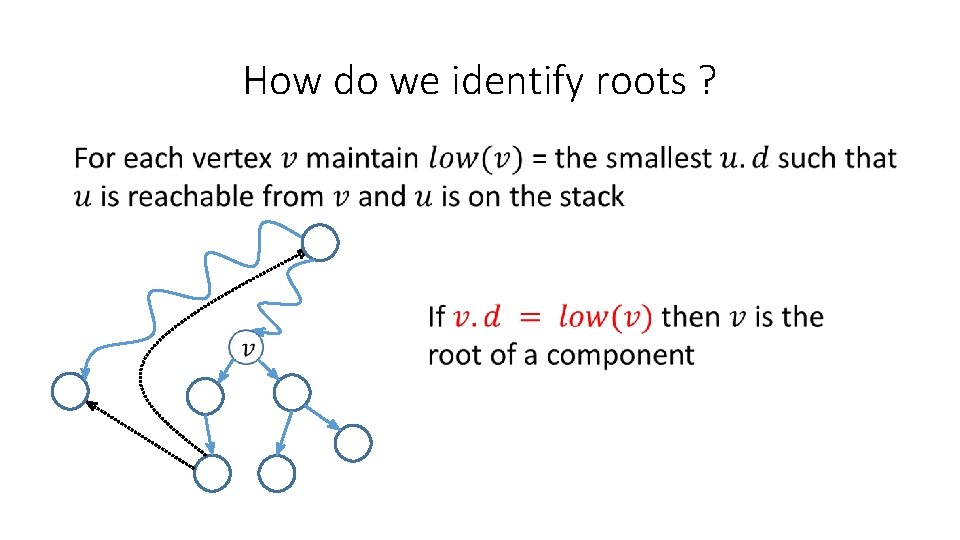
How do we identify roots ? .

Identify the roots of these subtrees 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19

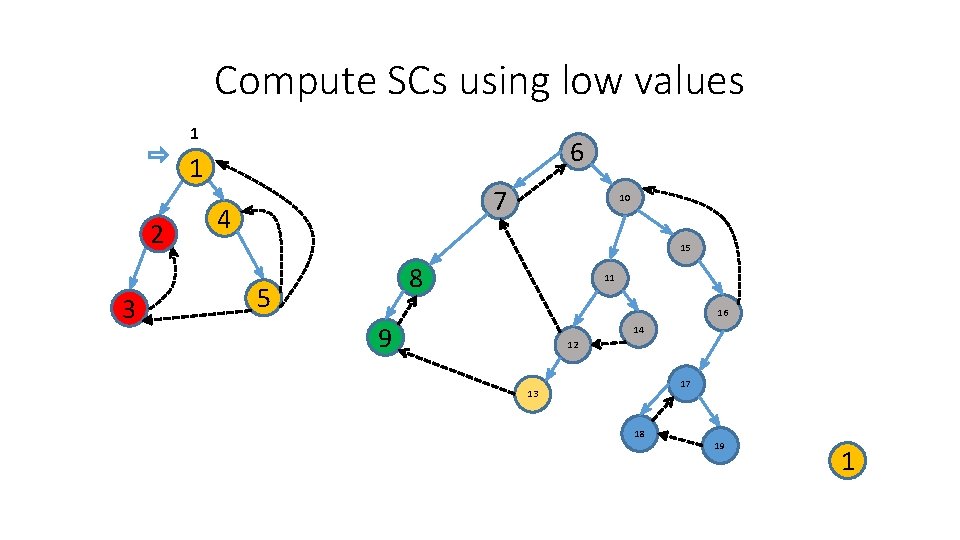
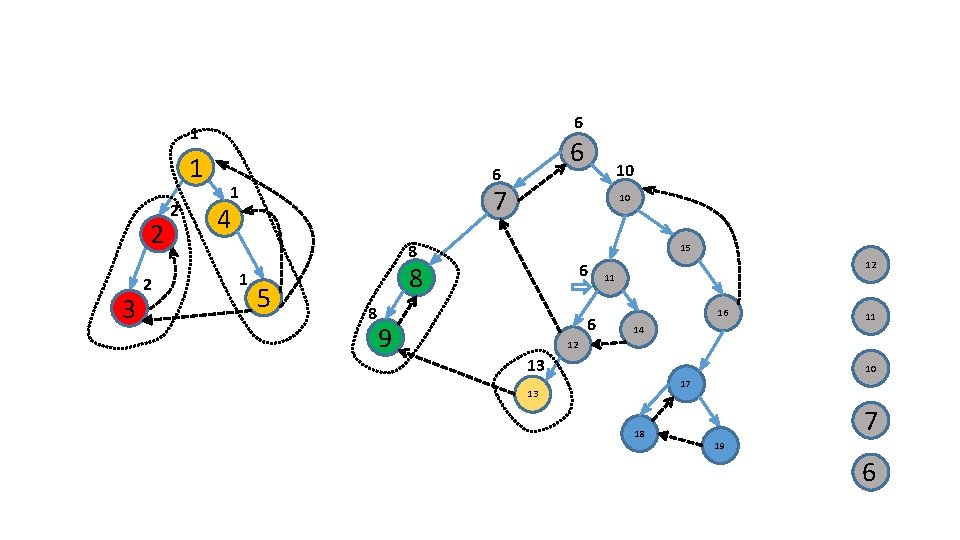
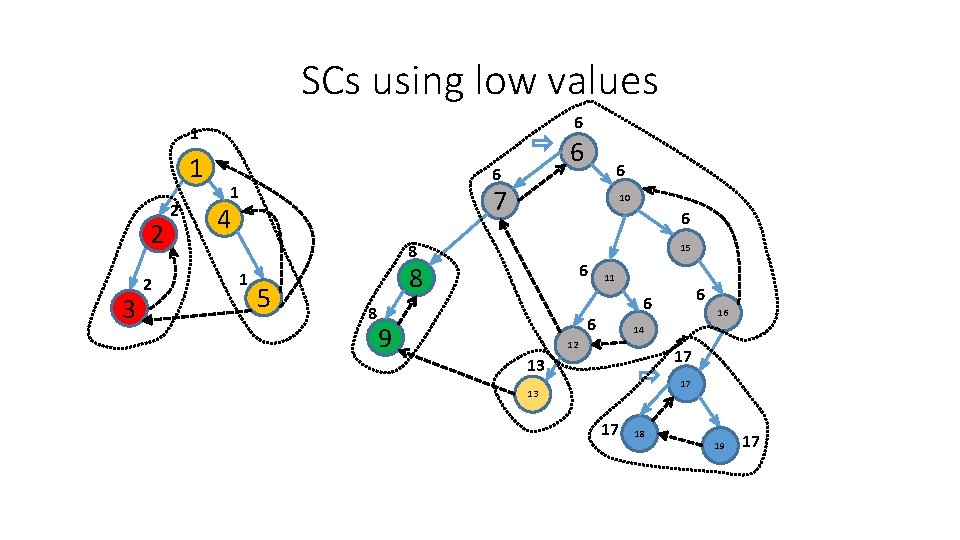
Compute SCs using low values 1 6 1 2 3 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19 1

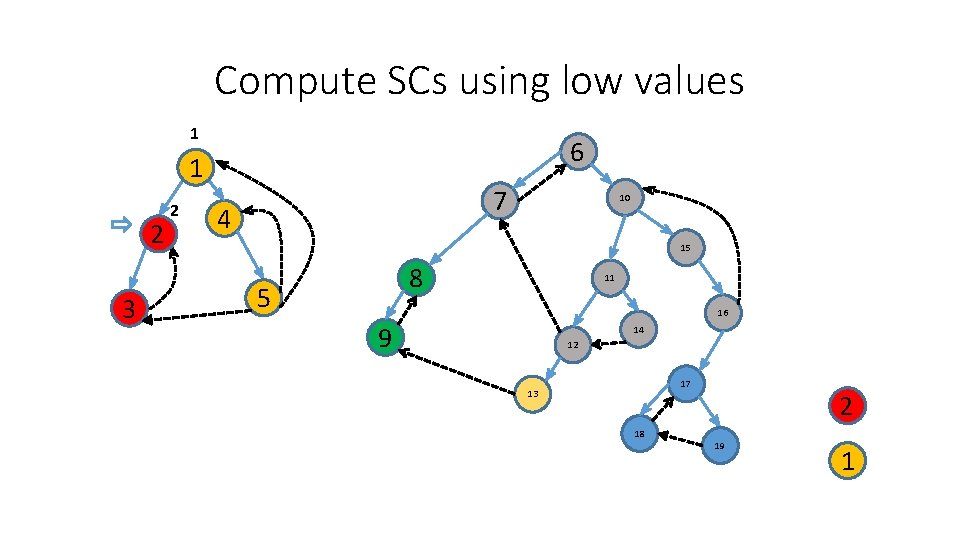
Compute SCs using low values 1 6 1 2 3 2 7 4 10 15 8 5 11 16 9 14 12 17 13 18 2 19 1

1 6 1 2 3 3 2 7 4 10 15 8 5 11 16 9 14 12 3 17 13 18 2 19 1

1 6 1 2 3 2 2 7 4 10 15 8 5 11 16 9 14 12 3 17 13 18 2 19 1

1 6 1 2 3 2 2 7 4 10 15 8 5 11 16 9 14 12 3 17 13 18 2 19 1

1 6 1 2 3 2 2 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19 1

1 6 1 2 3 2 2 7 4 10 15 8 5 11 16 9 14 12 17 13 18 19 1

1 1 2 3 2 2 6 4 7 4 10 15 8 5 11 16 9 14 12 17 13 18 4 19 1

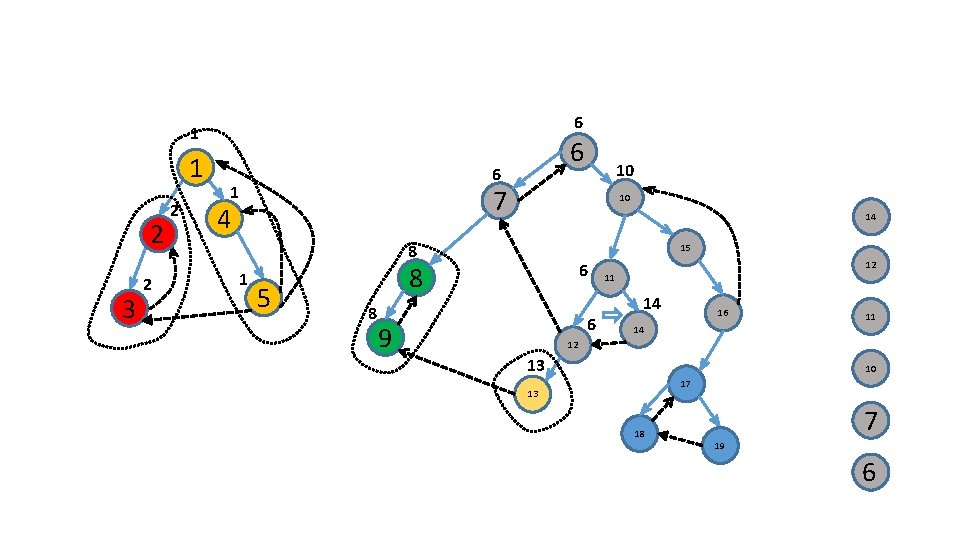
1 1 2 3 2 2 6 4 7 4 10 15 5 8 5 11 16 9 14 5 12 17 13 18 4 19 1

1 1 2 3 2 2 6 4 7 4 10 15 4 8 5 11 16 9 14 5 12 17 13 18 4 19 1

1 1 2 3 2 2 6 4 7 4 10 15 1 8 5 11 16 9 14 5 12 17 13 18 4 19 1

1 1 2 3 2 2 6 1 7 4 10 15 1 8 5 11 16 9 14 5 12 17 13 18 4 19 1

1 1 2 3 2 2 6 1 7 4 10 15 1 8 5 11 16 9 14 5 12 17 13 18 4 19 1

1 1 2 3 2 2 6 1 7 4 10 15 1 8 5 11 16 9 14 12 17 13 18 19

6 1 1 2 3 2 2 6 1 7 4 10 15 1 8 5 11 16 9 14 12 17 13 18 19 6

6 1 1 2 3 2 2 6 7 1 7 4 10 8 1 5 15 8 9 11 16 9 9 14 8 12 17 13 7 18 19 6

6 1 1 2 3 2 2 6 7 1 7 4 10 8 1 5 15 8 8 11 16 9 9 14 8 12 17 13 7 18 19 6

6 1 1 2 3 2 2 6 7 1 7 4 10 8 1 5 15 8 8 11 16 9 9 14 8 12 17 13 7 18 19 6

6 1 1 2 3 2 2 6 7 1 7 4 10 8 1 5 15 8 8 11 16 9 14 12 17 13 7 18 19 6

6 1 1 2 3 2 2 6 6 1 7 4 10 8 1 5 15 8 8 11 16 9 14 12 17 13 7 18 19 6

6 1 1 2 3 2 2 6 6 1 7 4 10 8 1 10 5 15 11 8 8 12 11 12 9 16 11 14 12 10 17 13 18 7 19 6

6 1 1 2 3 2 2 6 6 1 7 4 10 8 1 10 5 15 11 8 8 6 9 12 11 16 11 14 12 10 17 13 18 7 19 6

6 1 1 2 3 2 2 6 6 1 7 4 10 13 8 1 10 5 15 11 8 8 9 6 12 11 16 11 14 12 13 10 17 13 18 7 19 6

6 1 1 2 3 2 2 6 6 1 7 4 10 8 1 10 5 15 11 8 8 9 6 12 11 16 11 14 12 13 10 17 13 18 7 19 6

6 1 1 2 3 2 2 6 6 1 7 4 10 8 1 10 5 15 6 8 8 9 6 12 11 16 11 14 12 13 10 17 13 18 7 19 6

6 1 1 2 3 2 2 6 6 1 7 4 10 14 8 1 10 5 15 6 8 8 9 6 12 11 14 16 11 14 12 13 10 17 13 18 7 19 6

6 1 1 2 3 2 2 6 6 1 7 4 10 14 8 1 10 5 15 6 8 8 9 6 12 11 6 16 11 14 12 13 10 17 13 18 7 19 6

6 1 1 2 3 2 2 6 6 1 7 4 10 14 8 1 6 5 15 6 8 8 9 6 12 11 6 16 11 14 12 13 10 17 13 18 7 19 6

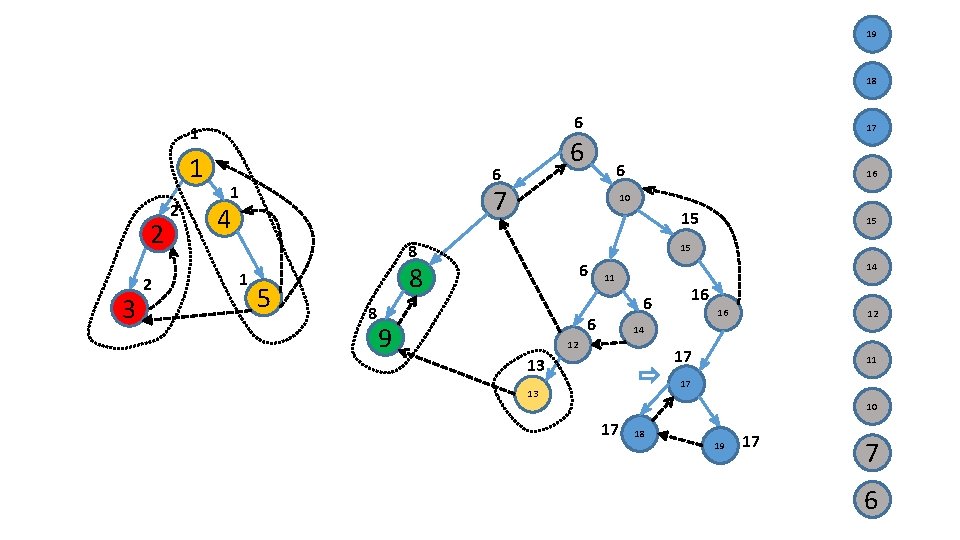
6 1 1 2 3 2 2 6 6 1 7 4 5 15 9 14 15 6 8 8 15 10 8 1 6 6 12 11 6 16 11 14 12 13 10 17 13 18 7 19 6

19 18 6 1 1 2 3 2 2 6 6 1 6 7 4 5 15 9 15 15 6 8 8 16 10 8 1 17 14 11 6 6 16 16 12 14 12 17 13 11 17 13 10 17 18 19 17 7 6

6 1 1 2 3 2 2 6 6 1 7 4 5 15 9 15 15 6 8 8 16 10 8 1 6 14 11 6 6 16 16 12 14 12 17 13 11 17 13 10 17 18 19 17 7 6

SCs using low values 6 1 1 2 3 2 2 6 6 1 7 4 10 6 8 1 6 5 15 6 8 8 9 11 6 6 6 16 14 12 17 13 17 18 19 17

Tarjan’s algorithm