Dependability Maintainability Theory and Methods 3 Reliability Block

Dependability & Maintainability Theory and Methods 3. Reliability Block Diagrams Andrea Bobbio Dipartimento di Informatica Università del Piemonte Orientale, “A. Avogadro” 15100 Alessandria (Italy) bobbio@unipmn. it - http: //www. mfn. unipmn. it/~bobbio/IFOA A. Bobbio IFOA, Reggio Emilia, June 2003 17 -18, 2003 Reggio Emilia, June 17 -18,

Model Types in Dependability Combinatorial models assume that components are statistically independent: poor modeling power coupled with high analytical tractability. Reliability Block Diagrams, FT, …. State-space models rely on the specification of the whole set of possible states of the system and of the possible transitions among them. CTMC, Petri nets, …. A. Bobbio Reggio Emilia, June 17 -18, 2003 2

Reliability Block Diagrams q Each component of the system is represented as a block; q System behavior is represented by connecting the blocks; q Failures of individual components are assumed to be independent; q Combinatorial (non-state space) model type. A. Bobbio Reggio Emilia, June 17 -18, 2003 3

Reliability Block Diagrams (RBDs) 1. Schematic representation or model; 2. Shows reliability structure (logic) of a system; 3. Can be used to determine dependability measures; 4. A block can be viewed as a “switch” that is “closed” when the block is operating and “open” when the block is failed; 5. System is operational if a path of “closed switches” is found from the input to the output of the diagram. A. Bobbio Reggio Emilia, June 17 -18, 2003

Reliability Block Diagrams (RBDs) Can be used to calculate: – Non-repairable system reliability given: Ø Individual block reliabilities (or failure rates); Ø Assuming mutually independent failures events. – Repairable system availability given: v. Individual block availabilities (or MTTFs and MTTRs); v. Assuming mutually independent failure and restoration events; v. Availability of each block is modeled as 2 -state Markov chain. A. Bobbio Reggio Emilia, June 17 -18, 2003

Series system in RBD Series system of n components. A 1 A 2 An Components are statistically independent Define event Ei = “component i functions properly. ” P(Ei) is the probability “component i functions properly” Ø the reliability R i(t) (non repairable) Ø the availability A i(t) (repairable) A. Bobbio Reggio Emilia, June 17 -18, 2003

Reliability of Series system of n components. A 1 A 2 An Components are statistically independent Define event Ei = "component i functions properly. ” Denoting by R i(t) the reliability of component i Product law of reliabilities: A. Bobbio Reggio Emilia, June 17 -18, 2003

Series system with time-independent failure rate Let i be the time-independent failure rate of component i. - it Then: Ri (t) = e The system reliability Rs(t) becomes: Rs(t) = e A. Bobbio - st n with s = i 1 1 MTTF = ———— s n i i=1 Reggio Emilia, June 17 -18, 2003 i=1

Availability for Series System Assuming independent repair for each component, where Ai is the (steady state or transient) availability of component i A. Bobbio Reggio Emilia, June 17 -18, 2003

Series system: an example A. Bobbio Reggio Emilia, June 17 -18, 2003

Series system: an example A. Bobbio Reggio Emilia, June 17 -18, 2003

Improving the Reliability of a Series System Sensitivity analysis: Si= Rs ———— = Ri Rs ———— Ri The optimal gain in system reliability is obtained by improving the least reliable component. A. Bobbio Reggio Emilia, June 17 -18, 2003

The part-count method It is usually applied for computing the reliability of electronic equipment composed of boards with a large number of components. Components are connected in series and with timeindependent failure rate. A. Bobbio Reggio Emilia, June 17 -18, 2003

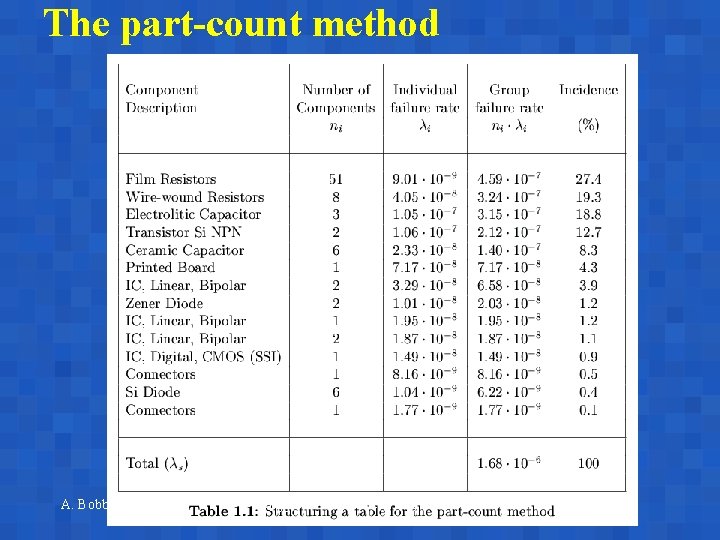
The part-count method A. Bobbio Reggio Emilia, June 17 -18, 2003

Redundant systems When the dependability of a system does not reach the desired (or required) level: v Improve the individual components; v Act at the structure level of the system, resorting to redundant configurations. A. Bobbio Reggio Emilia, June 17 -18, 2003

Parallel redundancy A system consisting of n independent components in parallel. It will fail to function only if all n components have failed. Ei = “The component i is functioning” Ep = “the parallel system of n component is functioning properly. ” A. Bobbio Reggio Emilia, June 17 -18, 2003 A 1. . . An

Parallel system Therefore: A. Bobbio Reggio Emilia, June 17 -18, 2003

Parallel redundancy — Fi (t) = P (Ei) Probability component i is not functioning (unreliability) Ri (t) = 1 - Fi (t) = P (Ei) Probability component i is functioning (reliability) Fp (t) = n i=1 Fi (t) n Rp (t) = 1 - Fp (t) = 1 - (1 - Ri (t)) i=1 A. Bobbio Reggio Emilia, June 17 -18, 2003 A 1. . . An

2 -component parallel system For a 2 -component parallel system: A 1 Fp (t) = F 1 (t) F 2 (t) A 2 Rp (t) = 1 – (1 – R 1 (t)) (1 – R 2 (t)) = = R 1 (t) + R 2 (t) – R 1 (t) R 2 (t) A. Bobbio Reggio Emilia, June 17 -18, 2003

2 -component parallel system: constant failure rate For a 2 -component parallel system A 1 with constant failure rate: A 2 Rp (t) = e - 1 t +e 1 1 MTTF = —— + —— 1 A. Bobbio 2 - 2 t – – e - ( 1 + 2 ) t 1 ———— 1 + 2 Reggio Emilia, June 17 -18, 2003

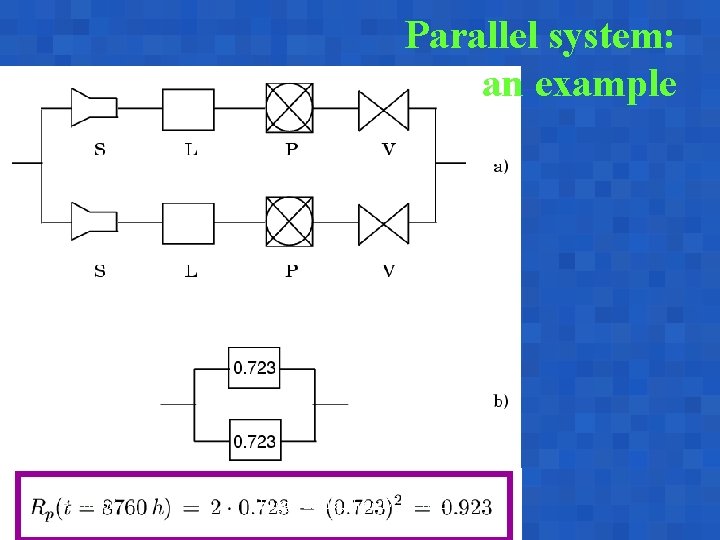
Parallel system: an example A. Bobbio Reggio Emilia, June 17 -18, 2003

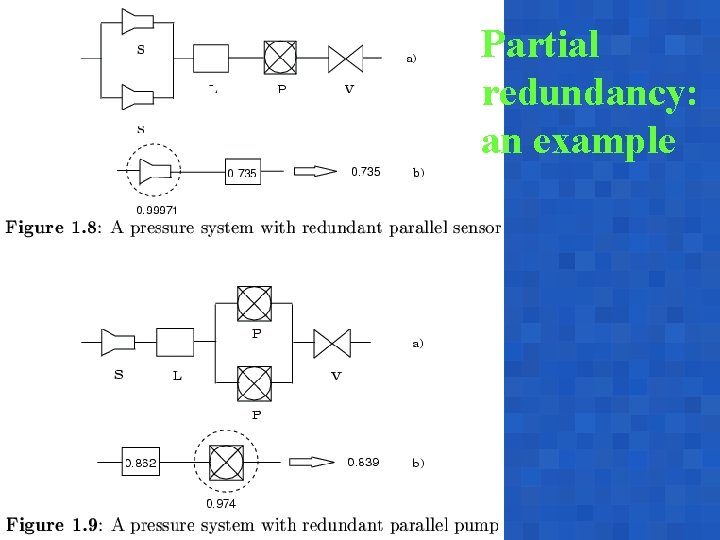
Partial redundancy: an example A. Bobbio Reggio Emilia, June 17 -18, 2003

Availability for parallel system Assuming independent repair, where Ai is the (steady state or transient) availability of component i. A. Bobbio Reggio Emilia, June 17 -18, 2003

Series-parallel systems A. Bobbio Reggio Emilia, June 17 -18, 2003

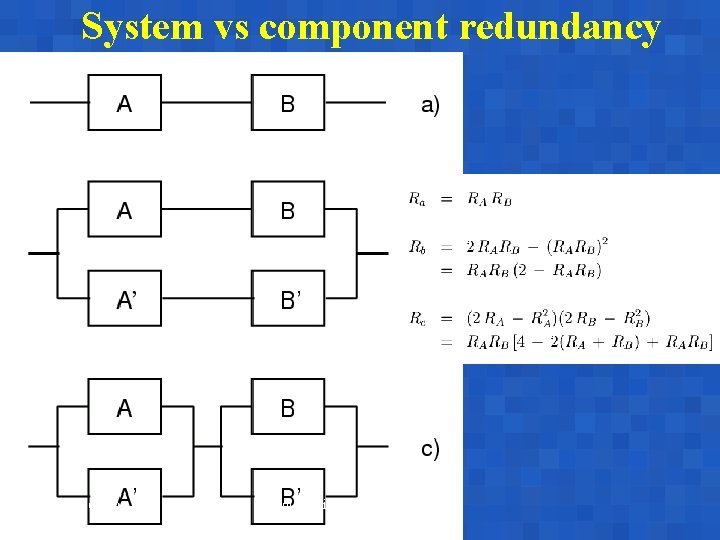
System vs component redundancy A. Bobbio Reggio Emilia, June 17 -18, 2003

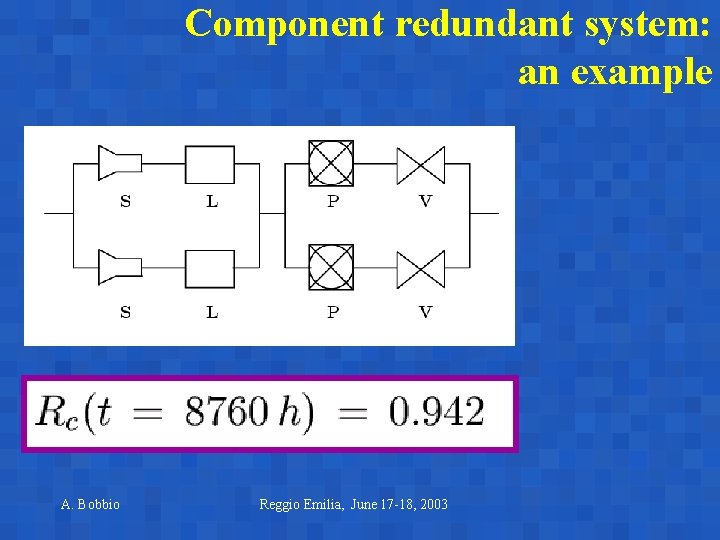
Component redundant system: an example A. Bobbio Reggio Emilia, June 17 -18, 2003

Is redundancy always useful ? A. Bobbio Reggio Emilia, June 17 -18, 2003

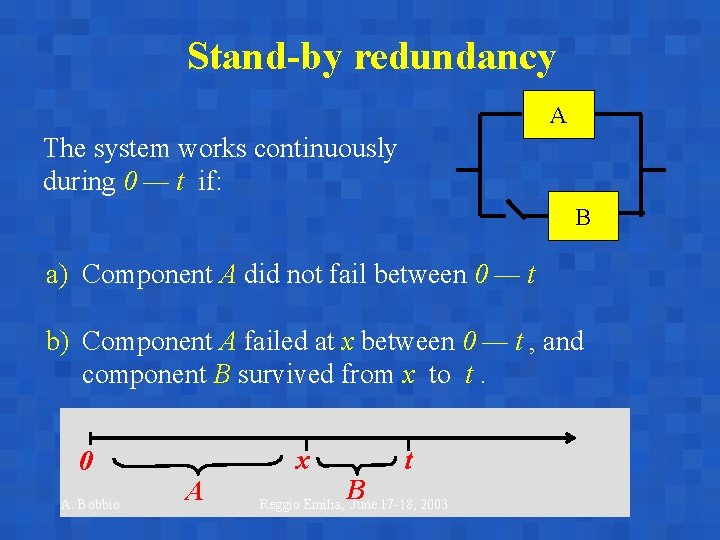
Stand-by redundancy A The system works continuously during 0 — t if: B a) Component A did not fail between 0 — t b) Component A failed at x between 0 — t , and component B survived from x to t. 0 A. Bobbio x A B t Reggio Emilia, June 17 -18, 2003

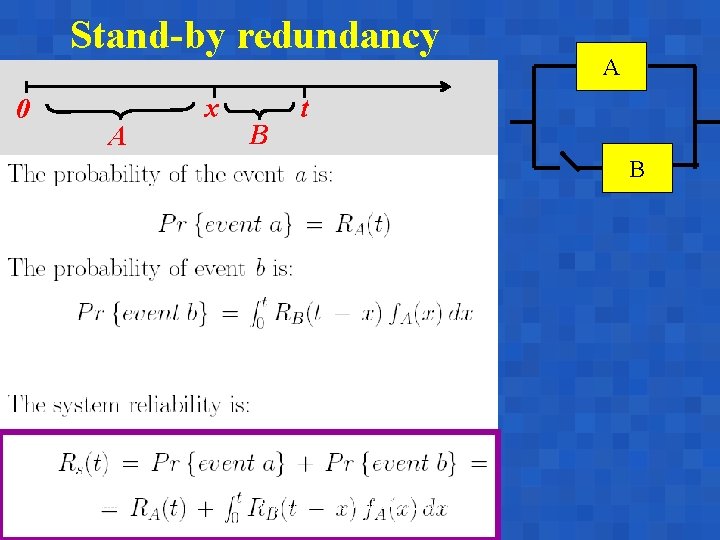
Stand-by redundancy 0 A x B A t B A. Bobbio Reggio Emilia, June 17 -18, 2003

Stand-by redundancy (exponential components) A B A. Bobbio Reggio Emilia, June 17 -18, 2003

Majority voting redundancy A 1 A 2 A 3 A. Bobbio Reggio Emilia, June 17 -18, 2003 Voter

2: 3 majority voting redundancy A 1 Voter A 2 A 3 A. Bobbio Reggio Emilia, June 17 -18, 2003