DEPARTMENT OF QUANTITATIVE METHODS INFORMATION SYSTEMS Introduction to





























































- Slides: 65

DEPARTMENT OF QUANTITATIVE METHODS & INFORMATION SYSTEMS Introduction to Business Statistics QM 120 Chapter 4

Experiment, outcomes, and sample space 2 Ø Ø Ø Probability and statistics are related in an important way. It is used to allow us to evaluate the reliability of our conclusions about the population when we have only sample information. Data are obtained by observing either uncontrolled events in nature or controlled situation in laboratory. We use the term experiment to describe either method of data collection. The observation or measurement generated by an experiment may or may not produce a numerical value. Here are some examples: Ø Ø Recording a test grade Interviewing a householder to obtain his or her opinion in certain issue.

Experiment, outcomes, and sample space 3 Table 1: Examples of experiments, outcomes, and sample spaces Ø Experiment Outcomes Sample Space Toss a coin once Head, Tail S = {Head, Tail} Roll a die once 1, 2, 3, 4, 5, 6 S = {1, 2, 3, 4, 5, 6} Play a lottery Win, Lose S = {Win, Lose} Select a student M, F S = {M, F} Toss a coin twice HH, HT, TH, TT S = {HH, HT, TH, TT} Venn diagram is a picture that depicts all possible outcomes for an experiment while in tree diagram, each outcome is represented a branch of a tree. H ●H ●T Venn Diagram T Tree Diagram

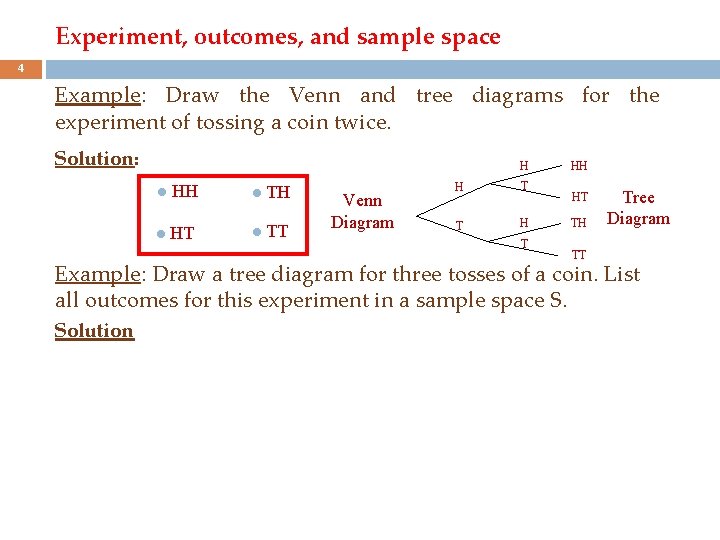
Experiment, outcomes, and sample space 4 Example: Draw the Venn and tree diagrams for the experiment of tossing a coin twice. Solution: H ● HH ● TH ● HT ● TT Venn Diagram H T T HH HT TH TT Tree Diagram Example: Draw a tree diagram for three tosses of a coin. List all outcomes for this experiment in a sample space S. Solution

Experiment, outcomes, and sample space 5 A simple event is the outcome that is observed on a single repetition of the experiment. It is often denoted by E with a subscript. Example: Toss a die and observe the number that appears on the upper face. List the simple event in the experiment. Solution: When the die is tossed once, there are six possible outcomes. There are the simple events, listed below. Event E 1: Observe a 1 Event E 2: Observe a 2 Event E 3: Observe a 3 Event E 4: Observe a 4 Event E 5: Observe a 5 Event E 6: Observe a 6

Experiment, outcomes, and sample space 6 We can now define an event (or compound event) as a collection of simple events, often denoted a capital letter. Example: Tossing a die (continued) We can define the events A and B as follow, A: Observe an odd number B: Observe a number less than 4 Solution:

Experiment, outcomes, and sample space 7 Example: Suppose we randomly select two persons from members of a club and observe whether the person selected is a man or woman. Write all the outcomes from experiment. Draw the Venn and tree diagrams for this experiment. Solution: Ø Ø Two events are mutually exclusive if, when one event occurs, the other cannot, and vice versa. The set of all simple events is called the sample space, S.

Calculating Probability 8 Probability is a numerical measure of the likelihood that an event will occur. Ø Two properties of probability Ø The probability of an even always lies in the range 0 to 1. 0 ≤ P(Ei) ≤ 1 0 ≤ P(A) ≤ 1 Ø The sum of the probabilities of all simple events for an experiment, denoted by ΣP(Ei), is always 1. ∑ P(Ei) = P(E 1) + P(E 2) + P(E 3) +. . =1

Calculating Probability 9 Three conceptual approaches to probability 1. Classical probability Ø Ø Ø Two or more events that have the same probability of occurrence are said to be equally likely events. The probability of a simple event is equal to 1 divided by the total number of all final outcomes for an equally likely experiment. Classical probability rule to find probability

Calculating Probability 10 Example: Find the probability of obtaining a head and the probability of obtaining a tail for one toss of a coin. Solution

Calculating Probability 11 Example: Find the probability of obtaining an even number in one roll of a die. Solution

Calculating Probability 12 Calculating the probability of an event: Ø List all the simple events in the sample space. Ø Assign an appropriate probability to each simple event. Ø Determine which simple events result in the event of interest. Ø Sum the probabilities of the simple events that result in the event of interest. Always 1. Include all simple events in the sample space. 2. Assign realistic probabilities to the simple events.

Calculating Probability 13 Example: A six years boy has a safe box that contains four banknotes: One-Dinar, Five-Dinar, Ten-Dinar, Twenty-Dinar. His sister which is a three years old girl randomly grabbed three banknotes from the safe box to buy a 30 KD toy. Find the odds (probability) that this girl can buy the toy. Solution

Calculating Probability 14 2. Relative frequency concept of probability Ø Ø Suppose we want to know the following probabilities: Ø The next car coming out of an auto factory is a “lemon” Ø A randomly selected family owns a home Ø A randomly selected woman has never smoked The outcomes above are neither equally likely nor fixed for each sample. The variation goes to zero as n becomes larger and larger If an experiment is repeated n times and an event A is observed f times, then

Calculating Probability 15 Example: In a group of 500 women, 80 have played golf at least once. Suppose one of these 500 woman is selected. What is the probability that she played golf at least once Solution

Calculating Probability 16 Example: Ten of the 500 randomly selected cars manufactured at a certain auto factory are found to be defective. What is the probability that the next car manufactured at that factory is a defective? Solution:

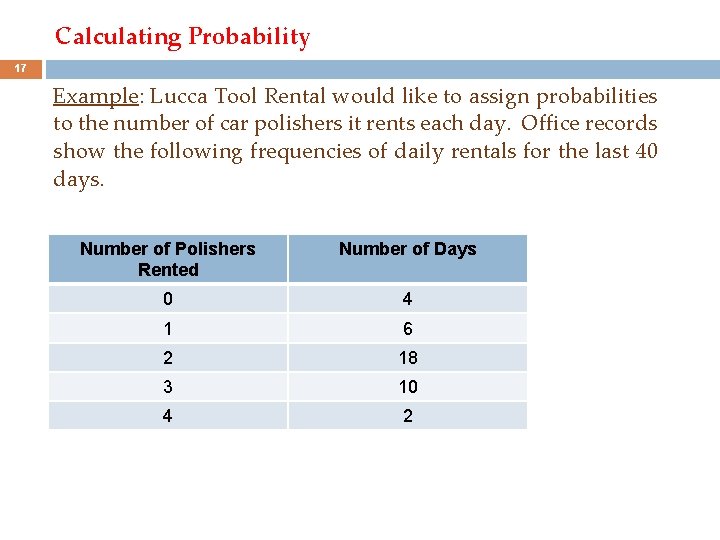
Calculating Probability 17 Example: Lucca Tool Rental would like to assign probabilities to the number of car polishers it rents each day. Office records show the following frequencies of daily rentals for the last 40 days. Number of Polishers Rented Number of Days 0 4 1 6 2 18 3 10 4 2

Calculating Probability 18 Solution

Calculating Probability 19 Law of large numbers: If an experiment is repeated again and again, the probability of an event obtained from the relative frequency approaches the actual probability. 3. Subjective probability Ø Ø Suppose we want to know the following probabilities: Ø A student who is taking a statistics class will get an A grade. Ø KSE price index will be higher at the end of the day. Ø China will dominate the gold medal list in the 2008 Olympics. Subjective probability is the probability assigned to an event based on subjective judgment, experience, information, and belief.

Counting Rule 20 Suppose that an experiment involves a large number N of simple events and you know that all the simple events are equally likely. Then each simple event has probability 1/N and the probability of an event A can be calculated as Ø The mn rule Ø Consider an experiment that is performed in two stages. If the first stage can be performed in m ways and for each of these ways, the second stage can be accomplished in n ways, then there mn ways to accomplish the experiment

Counting Rule 21 Example: Suppose you want to order a car in one of three styles and in one of four paint colors. To find out how many options are available, you can think of first picking one of the m = 3 styles and then one of n = 4 colors. Style Color 1 2 1 3 4 1 2 Using the mn rule, as shown in the figure below, you have mn= (3)(4) = 12 possible options. 2 3 4 1 2 3 3 4

Counting Rule 22 The extended mn rule Ø If an experiment is performed in k stages, with n 1 ways to accomplish the first stage, n 2 to accomplish the second stage…, and nk ways to accomplish the kth stage, the number of ways to accomplish the experiment is Example: A bus driver can take three routes from city A to city B, four routes from city B to city C, and three routes from city C to city D. For traveling from A to D, the driver must drive from A to B to C to D, how many possible routes from A to D are available

Counting Rule 23 Example: A couple is planning their weeding reception. The bird's parents have given thema choice of four reception facilities, three caterers, five DJs, and two limo services. He the couple randomly selects one reception facility, one caterer, one DJ, and one limo service, how many different outcomes are possible? .

Counting Rule 24 A counting rule for permutations (orderings) Ø The number of ways we can arrange n distinct objects, taking them r at a time, is A counting rule for combination Ø The number of distinct combinations of n distinct objects that can be formed, taking them r at a time, is

Counting Rule 25 Ø Ø Permutations: Given that position (order) is important, if one has 5 different objects (e. g. A, B, C, D, and E), how many unique ways can they be placed in 3 positions (e. g. ADE, AED, DEA, DAE, EAD, EDA, ABC, ACB, BCA, BAC etc. ) Combinations: If one has 5 different objects (e. g. A, B, C, D, and E), how many ways can they be grouped as 3 objects when position does not matter (e. g. ABC, ABD, ABE, ACD, ACE, ADE are correct but CBA is not ok as is equal to ABC)

Marginal & Conditional Probabilities 26 Ø Suppose all 100 employees of a company were asked whether they are in favor of or against paying high salaries to CEOs of U. S. companies. The following table gives a twoway classification of their responses. In favor Against Male 15 45 60 Female 4 36 40 19 81 100 Total Ø Total Marginal probability is the probability of a single event without consideration of any other event

Marginal & Conditional Probabilities 27 Ø Ø Ø Suppose one employee is selected, he/she maybe classified either on the bases of gender alone or on the bases of opinion. The probability of each of the following event is called marginal probability Ø P(male) = 60/100 Ø P(female) = 40/100 Ø Ø In favor Against Total Male 15 45 60 P(in favor) = 19/100 Female 4 36 40 P(against) = 81/100 Total 19 81 100 Suppose the employee selected is known to be male. What is the probability that he is in favor?

Marginal & Conditional Probabilities 28 Ø This probability is called conditional probability and is written as “the probability that the employee selected is in favor given that he is a male. ” P( in favor | male ) The event whose probability is to be determined Ø This event has already occurred Read as “given” Conditional probability is the probability that an even will occur given that another event has already occurred. If A and B are two events, then the conditional probability of A given B is written as P(A | B )

Marginal & Conditional Probabilities 29 Example: Find the conditional probability P(in favor | male) for the data on 100 employees Solution

Marginal & Conditional Probabilities 30 Example: Find the conditional probability P(female|in favor) for the data on 100 employees Solution

Marginal & Conditional Probabilities 31 Example: Consider the experiment of tossing a fair die. Denote by A and B the following events: A={Observing an even number}, B={Observing a number of dots less than or equal to 3}. Find the probability of the event A, given the event B. Solution

Mutually Exclusive Events 32 Ø Events that cannot occur together are called mutually exclusive events. Example: Consider the following events for one roll of a die A: an even number is observed = {2, 4, 6} B: an odd number is observed = {1, 3, 5} C: a number less than 5 is observed = {1, 2, 3, 4} - A and B are mutually exclusive events but A and C are not. - How about B and C? - Simple events are mutually exclusive always.

Independent vs. Dependent events 33 Ø Ø Two events are said to be independent if the occurrence of one does not affect the probability of the other one. A and B are said to be independent events if either P(A| B) = P(A) or P(B | A) = P(B) Example: Refer to the information on 100 employees. Are events “female (F)” and “in favor (A)” independent? Solution:

Independent vs. Dependent events 34 Ø What is the difference between mutually exclusive and independent events? Ø Ø Ø It is common to get confused or not to tell the difference between these two terminologies. When two events are mutually exclusive, they cannot both happen. Once the event B has occurred, event A cannot occur, so that P(A|B) = 0, or vice versa. The occurrence of event B certainly affects the probability that event A can occur. Therefore, Ø Mutually exclusive events must be dependent. Ø Independent events are never mutually exclusive. But, dependent events may or may not be mutually exclusive

Independent vs. Dependent events 35 Example: A sample of 420 people were asked if they smoke or not and whether they are graduate or not. The following two-way classification table gives their responses College graduate Not a college graduate Smoker 35 80 Nonsmoker 130 175 If an person is selected at random from this sample, find the probability that this person is a ØCollege graduate (G). ØNonsmoker (NS). ØSmoker (S) given the person is not a college graduate (NG). ØCollege graduate (G) given the person is a nonsmoker (NS). ØAre the events Smoker and college graduate independent? Why? Ø

Independent vs. Dependent events

Independent vs. Dependent events 37

Complementary Events 38 Ø Ø Two mutually exclusive events that taken together include all the outcome for an experiment (sample space, S) are called complementary events. Consider the following Venn diagram: The complement of event A, denoted by A and read as “A bar” or “A complement, ” is the event that includes B all the outcomes for an experiment that Venn diagram of two complementary evens are not in A Ø Since two complementary events, taken together, include all the sample space S, the sum of probabilities of all outcomes is 1 P(A) + P(A) = 1 - P(A)

Complementary Events 39 Example: In a lot of five machines, two are defective. If one of machines is randomly selected, what are the complementary events for this experiment and what are their probabilities? Solution: The two complementary events for this experiment are A = the machine selected is defective A = the machine selected is not defective Since there are 2 defective and three non defective machines, the probabilities of each event is P(A) = 2/5 = 0. 4 P(A) = 3/5 = 0. 6 or simply P(A) = 1 = 0. 4 = 0. 6

Intersection of Events & Multiplication Rule 40 Intersection of events Ø Let A and B be two events defined in a sample space. The intersection of A and B represents the collection of all outcomes that are common to both A and B is denoted by any of the followings A and B, A ∩ B, or AB Example: Let A = the event that a person owns a PC Let B = the event that a person owns a mobile A A and B B Intersection of events A and B

Intersection of Events & Multiplication Rule 41 Multiplication rule Ø Ø Sometimes we may need to find the probability of two events happening together. The probability of the intersection of two events A and B is called their joint probability. It is written P(AB) or P(A ∩ B) Ø Ø It can be obtained by multiplying the marginal probability of one event with the conditional probability of the second one. Multiplication rule: The probability of the intersection of two events A and B is P(AB) = P(A ∩ B) = P(A)P(B|A) = P(B)P(A|B)

Intersection of Events & Multiplication Rule 42 Example: The following table gives the classification of all employees of a company by gender and college degree. College graduate (G) Not a college graduate (N) Total Male (M) 7 20 27 Female (F) 4 9 13 Total 11 29 40 If one employee is selected at random, what is the probability that the employee is a female and a college graduate? Solution

Intersection of Events & Multiplication Rule

Intersection of Events & Multiplication Rule 44 Example: A box contains 20 DVD, 4 of which are defective. If two DVDs are selected at random (without replacement), what is the probability that both are defective? Solution:

Intersection of Events & Multiplication Rule 45 Ø If events A and B are independent, their joint probability simplifies from P(A ∩ B) = P(A)P(B |A) Ø TO P(A ∩ B) = P(A)P(B ) Sometimes we know the joint probability of two events A and B, in this case, the conditional probability of B given A or A given B is

Intersection of Events & Multiplication Rule 46 Example: According to a survey, 60% of all homeowners owe money on home mortgages. 36% owe money on both home mortgages and car loans. Find the conditional probability that a homeowner selected at random owes money on a car loan given that he owes money on a home mortgage. Solution:

Intersection of Events & Multiplication Rule 47 Example: A computer company has two quality control inspectors, Mr. Smith and Mr. Robertson, who independently inspect each computer before it is shipped to a client. The probability that Mr. Smith fails to detect a defective PC is. 02 while it is. 01 for Mr. Robertson. Find the probability that both inspectors will fail to detect a defective PC. Solution:

Intersection of Events & Multiplication Rule 48 Example: The probability that a patient is allergic to Penicillin is. 2. Suppose this drug is administrated to three patients. Find a) The probability that all three of them are allergic to it b) At least one of them is not allergic Solution: Let A = 1 st patient is allergic to penicillin B = 2 nd patient is allergic to penicillin C = 3 rd patient is allergic to penicillin

Union of Events & Addition Rule 49 Union of events Ø Let A and B be two events defined in a sample space S. The union of events A and B is the collection of all outcomes that belong either to A and B or to both A and B and is denoted by “ A or B” or “A ∪ B” S A B

Union of Events & Addition Rule 50 Example: A company has 1000 employees. Of them, 400 are females and 740 are labor union members. Of the 400 females, 250 are union members. Describe the union of events “female” and “union member” Solution

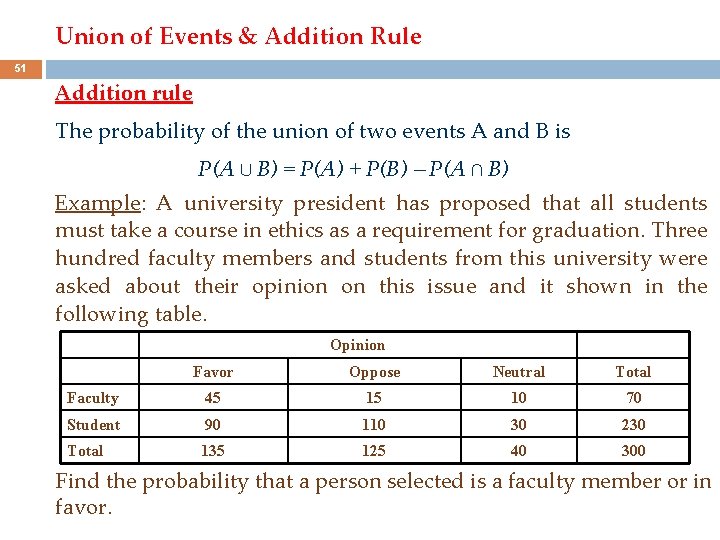
Union of Events & Addition Rule 51 Addition rule The probability of the union of two events A and B is P(A ∪ B) = P(A) + P(B) – P(A ∩ B) Example: A university president has proposed that all students must take a course in ethics as a requirement for graduation. Three hundred faculty members and students from this university were asked about their opinion on this issue and it shown in the following table. Opinion Favor Oppose Neutral Total Faculty 45 15 10 70 Student 90 110 30 230 Total 135 125 40 300 Find the probability that a person selected is a faculty member or in favor.

Union of Events & Addition Rule 52 Solution:

Union of Events & Addition Rule 53 Example: There a total of 7225 thousand persons with multiple jobs in the US. Of them, 4115 thousand are male, 1742 thousand are single, and 905 thousand are male and single. What is the probability that a selected person is a male or single? Solution:

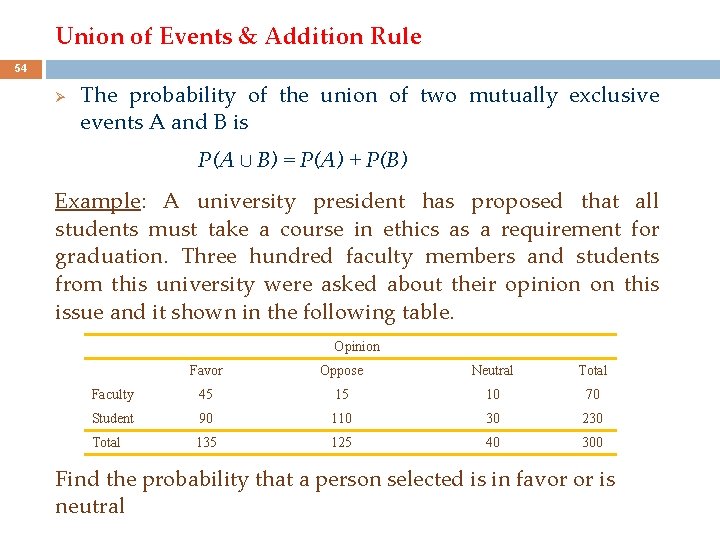
Union of Events & Addition Rule 54 Ø The probability of the union of two mutually exclusive events A and B is P(A ∪ B) = P(A) + P(B) Example: A university president has proposed that all students must take a course in ethics as a requirement for graduation. Three hundred faculty members and students from this university were asked about their opinion on this issue and it shown in the following table. Opinion Favor Oppose Neutral Total Faculty 45 15 10 70 Student 90 110 30 230 Total 135 125 40 300 Find the probability that a person selected is in favor or is neutral

Union of Events & Addition Rule 55 Solution:

Union of Events & Addition Rule 56 Example: Eighteen percent of the working lawyers in the United States are female. Two lawyers are selected at random and it is observed whether they are male or female. a) Draw a tree diagram for this experiment b) Find the probability that at least one of the two lawyers is a female. Solution:

Law of Total Probability & Bayes’ Rule Consider the following Venn diagram B 1 A 1 B B 2 Bn-1 A 2 An-1 Bn A An Can we find the area (probability) of A assuming that we know the probability of each Bi & P(A|Bi) ?

Law of Total Probability & Bayes’ Rule 58 Addition Law Multiplication Law Conditional Probability

Law of Total Probability & Bayes’ Rule 59 Bayes’ theorem (two-event case) Bayes’ theorem

Law of Total Probability & Bayes’ Rule 60 Example: Manufacturing firm that receives shipment of parts from two different suppliers. Currently, 65 percent of the parts purchased by the company are from supplier 1 and the remaining 35 percent are from supplier 2. Historical Data suggest the quality rating of the two supplier are shown in the table: Good Parts Bad Parts Supplier 1 98 2 Supplier 2 95 5 a) Draw a tree diagram for this experiment with the probability of all outcomes b) Given the information the part is bad, What is the probability the part came from supplier 1?

Law of Total Probability & Bayes’ Rule 61 Solution:

Law of Total Probability & Bayes’ Rule 62 Example: An insurance company rents 35% of the cars for its customers from Avis and the rest from Hertz. From past records they know that 8% of Avis cars break down and 5% of Hertz cars break down. A customer calls and complains that his rental car broke down. What is the probability that his car was rented from Avis?

Law of Total Probability & Bayes’ Rule 63 Solution:

Example 64 A study was recently done in which 500 people were asked to indicate their preferences for one of three products. The following table shows the breakdown of the responses by gender of the respondents. Gender Male Female Product Preference A B C 80 20 10 200 70 120 Suppose one person is randomly chosen. Based on this data, what is the probability that the person chose is a female who prefers product C? A). 31 B). 92 C). 86 D). 24

Example 65 The method of probability assessment that relies on an examination of historical data from similar situations is A) classical assessment B) relative frequency of occurrence C) subjective assessment D) historical assessment