Department of Mechanical Engineering ME 322 Mechanical Engineering

Department of Mechanical Engineering ME 322 – Mechanical Engineering Thermodynamics Lecture 36 Combustion Reactions

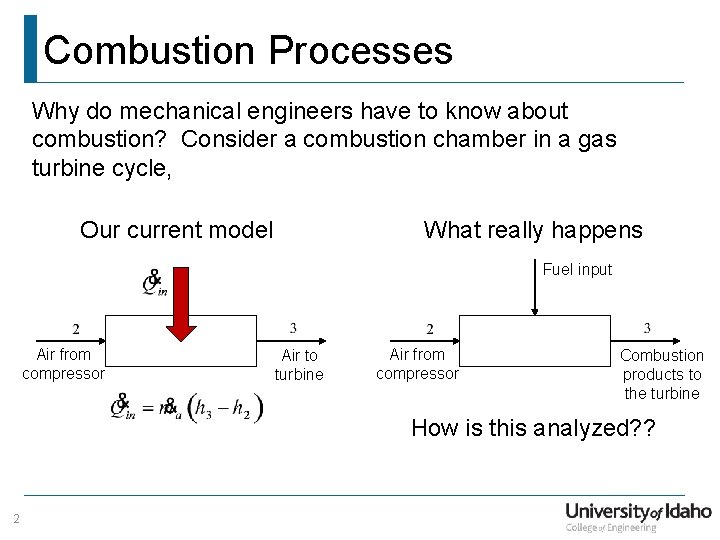
Combustion Processes Why do mechanical engineers have to know about combustion? Consider a combustion chamber in a gas turbine cycle, What really happens Our current model Fuel input Air from compressor Air to turbine Air from compressor Combustion products to the turbine How is this analyzed? ? 2

Combustion (ME Perspective) • Fuels – Stored chemical energy • Combustion Reaction – Transforms the chemical energy stored in the fuel to thermal energy (heat) • Goals for this lecture topic – Understand combustion chemistry – Understand terminology used in combustion – Solve some basic combustion problems 3

Combustion The combustion of a fuel requires oxygen, Reactants Products Fuel + Oxidant Products Fuel In the most general sense, a fossil fuel makeup is, The Greek letters signify the atomic composition of the fuel. For example. . . 4

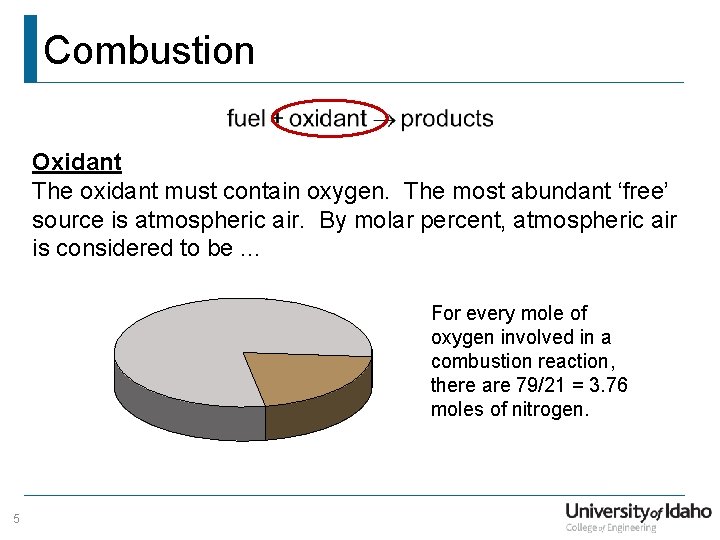
Combustion Oxidant The oxidant must contain oxygen. The most abundant ‘free’ source is atmospheric air. By molar percent, atmospheric air is considered to be. . . For every mole of oxygen involved in a combustion reaction, there are 79/21 = 3. 76 moles of nitrogen. 5

Combustion with Air as Oxidizer 1 mole of air is comprised of : ~0. 21 mole of Oxygen ~0. 79 mole of Nitrogen For balancing chemical equations we often write air as: 1 O 2 + 3. 76 N 2 Be careful as the above is not 1 mole of air. The above represents 4. 76 moles of air. This is especially important when Calculating molar AFR 6

Combustion Products (for fuels with no sulfur content) - Complete Combustion: CO 2, H 2 O, and N 2 - Incomplete Combustion: CO 2, H 2 O, N 2, CO, NOx - Combustion with Excess Oxygen: CO 2, H 2 O, N 2, and O 2 NOTE: Fuels containing sulfur have the potential of introducing sulfuric acid into the product stream. 7

Combustion Terminology • 8

Combustion Terminology In many combustion processes, one of the parameters we are interested in is how much air (or oxygen) is required per unit quantity (moles or mass) of fuel. Air-Fuel Ratio (AFR), and Fuel-Air Ratios 9

Combustion Terminology Dimensionless AFR: Want a way to describe if a mixture is stoichiometric, rich, or lean. Equivalence Ratio (combustion engineers) 10

Combustion Terminology Dimensionless AFR: Want a way to describe if a mixture is stoichiometric, rich, or lean. Lambda (engine calibration, mechanics) 11

Equivalence Ratio and Products • ME 322 Advanced courses 12

Stoichiometric (Complete) Combustion Stoichiometric Combustion of a General Fuel in Air Looks like 1 equation and 5 unknowns Atomic Balance Equations 5 equations 5 unknowns (n 0 through n 4) 13

Lean Combustion of a General Fuel in Excess Air PTA = Percent Theoretical Air expressed as a decimal 6 equations 6 unknowns (x 0 through x 5) Requires a stoichiometric balance first (to get n 0) 14

Two Example Problems Example 1 Given: Known fuel and theoretical air Find: A/F ratios (mass and molar), equivalence ratio, and dew point of water in combustion products Example 2 Given: Dried exhaust composition Find: Fuel composition, A/F ratio, and dew point 15

Example 1 – Octane Combustion Given: Gasoline (modeled as octane - C 8 H 18) burns completely in 150% theoretical air (or 50% excess air). Find: (a) the A/F ratios (mass and molar) (b) the equivalence ratio (c) the dew point of the products of combustion at assuming that the products are at 1 atm 16

Example 1 – Octane Combustion In order to calculate the air-fuel ratios and the equivalence ratio, we need to know how much air is used in the combustion reaction. This is determined by balancing the combustion reaction. In order to determine the dew point of the products, we need to know the molar composition of the products. This is also determined by balancing the combustion reaction. Everything depends on the correct balance of the combustion reaction! 17

Example 1 – Octane Combustion Solution strategy. . . 1. Balance the stoichiometric reaction to get n 0 2. Balance the reaction with 150% theoretical air 3. Calculate the required (A/F) ratios, the equivalence ratio, and the dew point temperature of the products 18

Example 1 – Octane Combustion Stoichiometric Reaction 19

Example 1 – Octane Combustion in 150% theoretical air 20

Example 1 – Octane Combustion The molar (A/F) ratio can now be found. . . 21

Example 1 – Octane Combustion The mass-based (A/F) ratio can be found knowing the molecular masses of the air and the fuel, The molecular mass of the air is, The molecular mass of the fuel is, 22

Example 1 – Octane Combustion Now, the mass-based (A/F) can be found. . . Once the (A/F) ratios are determined, the equivalence ratio can be found, 23

Example 1 – Octane Combustion The dew point of the products is the temperature where the water vapor condenses, Tdp = Tsat at Pw (partial pressure of the water vapor) 24

Example 2 – Problem 15. 42 Given: Combustion exhaust with 9. 1% CO 2, 8. 9% CO, 82% N 2, and no O 2 Find: a) Fuel Composition (Cn. Hm) b) Mass percentage of carbon and hydrogen in fuel c) Molar air/fuel ratio and percent theoretical air (PTA) d) Dew point temperature at. 106 MPa 25

Example 2 – Problem 15. 42 STEP 1: Write balance equation using ORSAT data Cn. Hm + a(O 2 + 3. 76 N 2) 9. 1 CO 2 + 8. 9 CO + b. H 2 O + 82 N 2 STEP 2: Solve for unknowns and write fuel model Cn. Hm n = 18 26 m = 33 a= 21. 8 b= 16. 5

Example 2 – Problem 15. 42 STEP 3: Compute molar mass of fuel & mass composition Mfuel = 18 lbmol. C/lbmolfuel*(12 lbm/lbmol. C) + 33 lbmol. H/lbmolfuel*(1 lbm/lbmol. H) = 249 lbm/lbmol fuel C: 18*(12)/249 87% H: 33*(1)/249 13% 27

Example 2 – Problem 15. 42 STEP 4: Calculate molar air/fuel ratio (actual reaction) 21. 8 * (1 + 3. 76) /1 = 103. 8 moles air / mole fuel STEP 5: Write equation for stoichiometric reaction C 18 H 33 + 26. 25(O 2 + 3. 76 N 2) 18 CO 2 + 16. 5 H 2 O + 98. 7 N 2 STEP 6: Find theoretical air %TA = (21. 8 / 26. 75) * 100 = 83% 28

Example 2 – Problem 15. 42 STEP 7: Find dew point of combustion products # moles of H 2 O (in original equation) = 16. 5 # moles of other combustion products = 100 # moles of all products (in original equation) = 116. 5 Pw =. 106 * (16. 5/116. 5) =. 015 Mpa Tsat (. 015 MPa) = 54 C 29