Department of Mathematics and Function Visualization 3 D

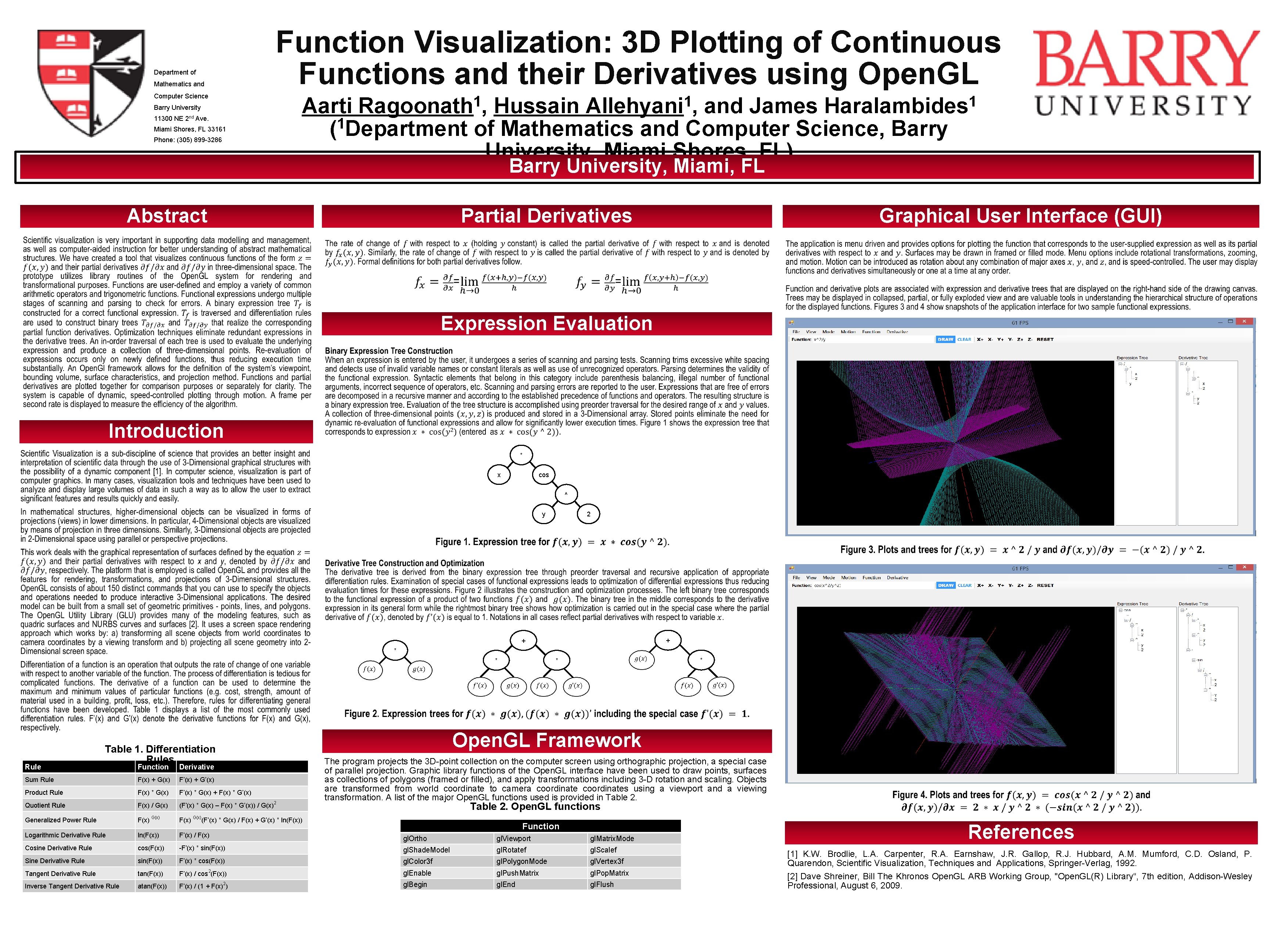
Department of Mathematics and Function Visualization: 3 D Plotting of Continuous Functions and their Derivatives using Open. GL Computer Science Barry University 11300 NE 2 nd Ave. Miami Shores, FL 33161 Phone: (305) 899 -3286 1 Ragoonath , 1 Allehyani , 1 Haralambides Aarti Hussain and James 1 ( Department of Mathematics and Computer Science, Barry University, Miami Shores, FL) Barry University, Miami, FL Partial Derivatives Graphical User Interface (GUI) H 2 O Abstract Expression Evaluation Introduction * x cos ^ y 2 + + * * Rule Table 1. Differentiation Rules * * Open. GL Framework Z= x^3/y^3 & Z’= 3 x^2/3 y^2 The program projects the 3 D-point collection on the computer screen using orthographic projection, a special case of parallel projection. Graphic library functions of the Open. GL interface have been used to draw points, surfaces as collections of polygons (framed or filled), and apply transformations including 3 -D rotation and scaling. Objects are transformed from world coordinate to camera coordinates using a viewport and a viewing transformation. A list of the major Open. GL functions used is provided in Table 2. Function Derivative Sum Rule F(x) + G(x) F’(x) + G’(x) Product Rule F(x) * G(x) F’(x) * G(x) + F(x) * G’(x) Quotient Rule F(x) / G(x) (F’(x) * G(x) – F(x) * G’(x)) / G(x)2 Generalized Power Rule F(x) G(x)(F’(x) * G(x) / F(x) + G’(x) * ln(F(x)) Logarithmic Derivative Rule ln(F(x)) F’(x) / F(x) gl. Ortho gl. Viewport gl. Matrix. Mode Cosine Derivative Rule cos(F(x)) -F’(x) * sin(F(x)) gl. Shade. Model gl. Rotatef gl. Scalef Sine Derivative Rule sin(F(x)) F’(x) * cos(F(x)) gl. Color 3 f gl. Polygon. Mode gl. Vertex 3 f Tangent Derivative Rule tan(F(x)) F’(x) / cos 2(F(x)) gl. Enable gl. Push. Matrix gl. Pop. Matrix Inverse Tangent Derivative Rule atan(F(x)) F’(x) / (1 + F(x)2) gl. Begin gl. End gl. Flush Table 2. Open. GL functions Function References [1] K. W. Brodlie, L. A. Carpenter, R. A. Earnshaw, J. R. Gallop, R. J. Hubbard, A. M. Mumford, C. D. Osland, P. Quarendon, Scientific Visualization, Techniques and Applications, Springer-Verlag, 1992. [2] Dave Shreiner, Bill The Khronos Open. GL ARB Working Group, "Open. GL(R) Library“, 7 th edition, Addison-Wesley Professional, August 6, 2009.