Department of Computer Eng Sharif University of Technology

Department of Computer Eng. Sharif University of Technology Discrete-time signal processing Chapter 4: Sampling of Continuous-Time Signals Content and Figures are from Discrete-Time Signal Processing, 2 e by Oppenheim, Shafer and Buck, © 1999 -2000 Prentice Hall Inc.

4. 1 Periodic Sampling • In this method x[n] obtained from xc(t) according to the relation : • The sampling operation is generally not invertible i. e. , given the output x[n] it is not possible in general to reconstruct xc(t). Although we remove this ambiguity by restricting xc(t). Chapter 4: Sampling of Continuous-Time Signals 1

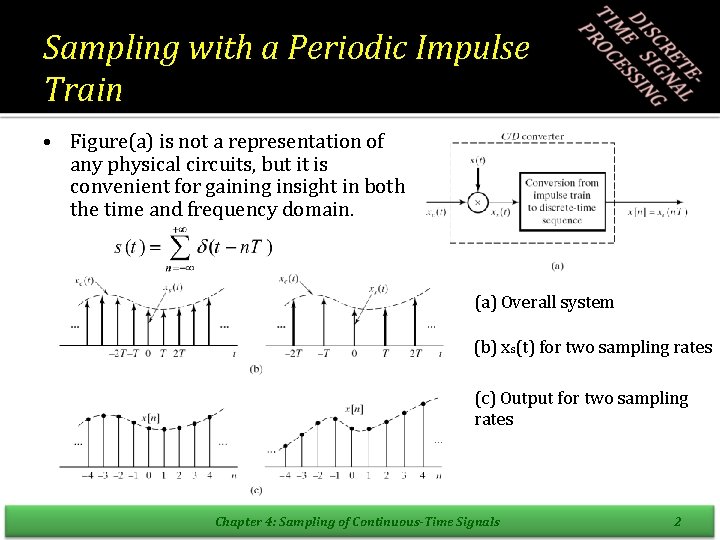
Sampling with a Periodic Impulse Train • Figure(a) is not a representation of any physical circuits, but it is convenient for gaining insight in both the time and frequency domain. (a) Overall system (b) xs(t) for two sampling rates (c) Output for two sampling rates Chapter 4: Sampling of Continuous-Time Signals 2

4. 2 Frequency Domain Representation of Sampling • Let us now consider the Fourier transform of xs(t): • If and Chapter 4: Sampling of Continuous-Time Signals 3

Frequency Domain Representation of Sampling • By applying the continuous-time Fourier transform to equation We obtain consequently Chapter 4: Sampling of Continuous-Time Signals 4

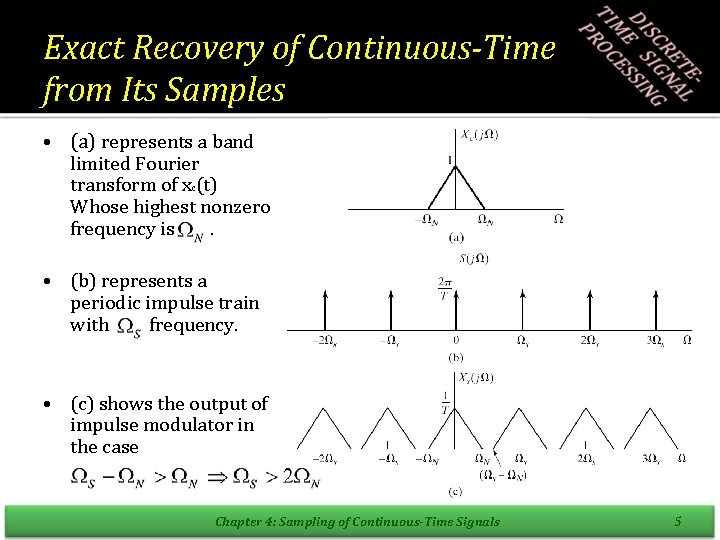
Exact Recovery of Continuous-Time from Its Samples • (a) represents a band limited Fourier transform of xc(t) Whose highest nonzero frequency is. • (b) represents a periodic impulse train with frequency. • (c) shows the output of impulse modulator in the case Chapter 4: Sampling of Continuous-Time Signals 5

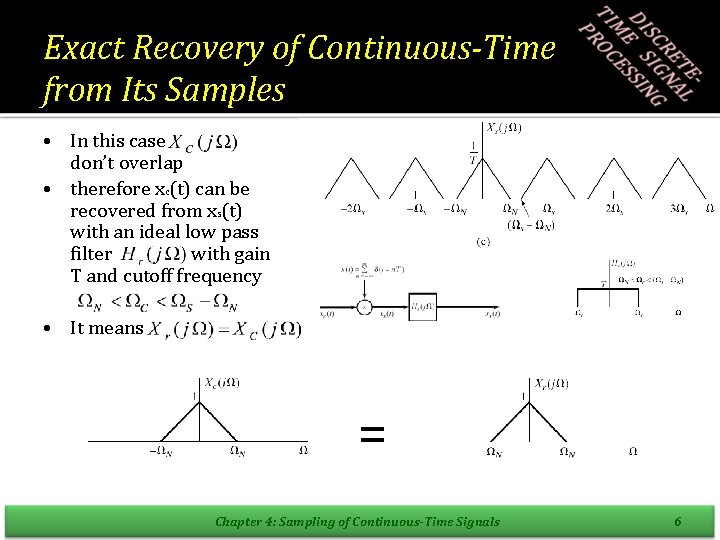
Exact Recovery of Continuous-Time from Its Samples • In this case don’t overlap • therefore xc(t) can be recovered from xs(t) with an ideal low pass filter with gain T and cutoff frequency • It means = Chapter 4: Sampling of Continuous-Time Signals 6

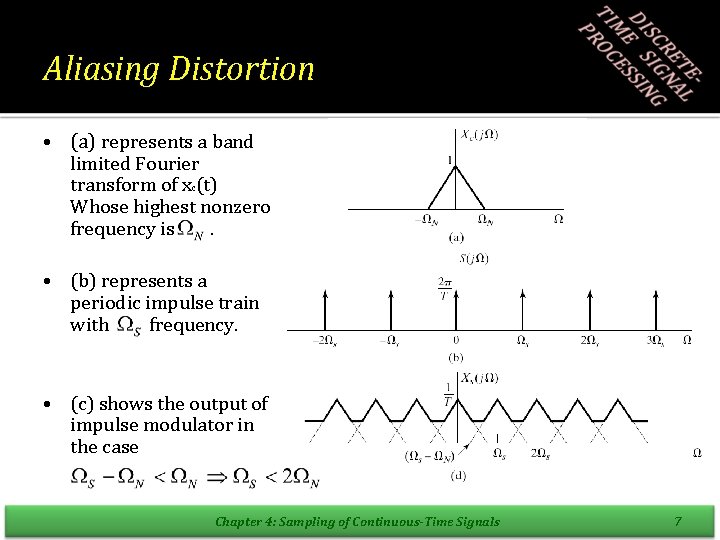
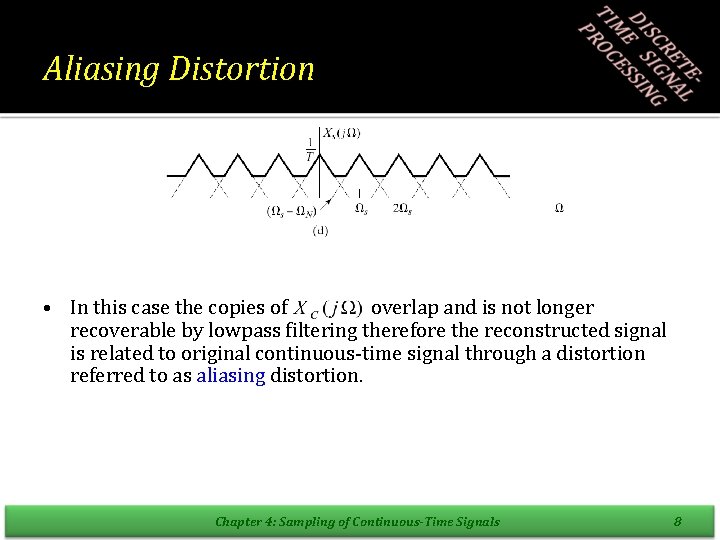
Aliasing Distortion • (a) represents a band limited Fourier transform of xc(t) Whose highest nonzero frequency is. • (b) represents a periodic impulse train with frequency. • (c) shows the output of impulse modulator in the case Chapter 4: Sampling of Continuous-Time Signals 7

Aliasing Distortion • In this case the copies of overlap and is not longer recoverable by lowpass filtering therefore the reconstructed signal is related to original continuous-time signal through a distortion referred to as aliasing distortion. Chapter 4: Sampling of Continuous-Time Signals 8

Example: The effect of aliasing in the sampling of cosine signal • Suppose Chapter 4: Sampling of Continuous-Time Signals 9

Nyquist Sampling Theorem • Sampling theorem describes precisely how much information is retained when a function is sampled, or whether a band-limited function can be exactly reconstructed from its samples. • Sampling Theorem: Suppose that to a frequency interval , i. e. , is band-limited Then xc(t) can be exactly reconstructed from equidistant samples where is the sampling period, frequency (samples/second), is the sampling is for radians/second. Chapter 4: Sampling of Continuous-Time Signals 10

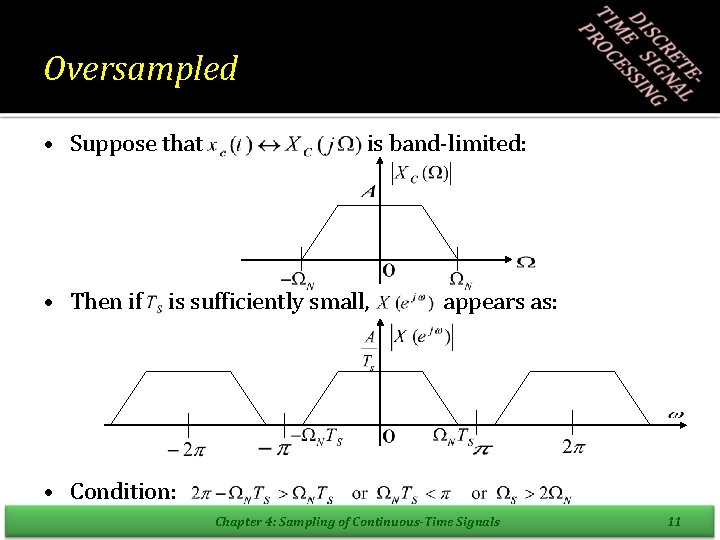
Oversampled • Suppose that • Then if is band-limited: is sufficiently small, appears as: • Condition: Chapter 4: Sampling of Continuous-Time Signals 11

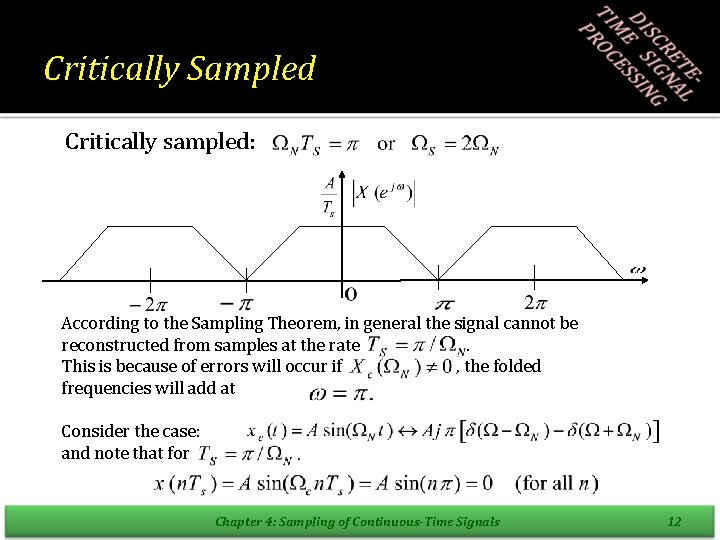
Critically Sampled Critically sampled: According to the Sampling Theorem, in general the signal cannot be reconstructed from samples at the rate. This is because of errors will occur if , the folded frequencies will add at Consider the case: and note that for Chapter 4: Sampling of Continuous-Time Signals 12

Undersampled (aliased) If sampling theorem condition is not satisfied • The frequencies are folded - summed. This changes the shape of the spectrum. There is no process whereby the added frequencies can be discriminated - so the process is not reversible. • Thus, the original (continuous) signal cannot be reconstructed exactly. Information is lost, and false (alias) information is created. • If a signal is not strictly band-limited, sampling can still be done at twice the effective band-limited. Chapter 4: Sampling of Continuous-Time Signals 13

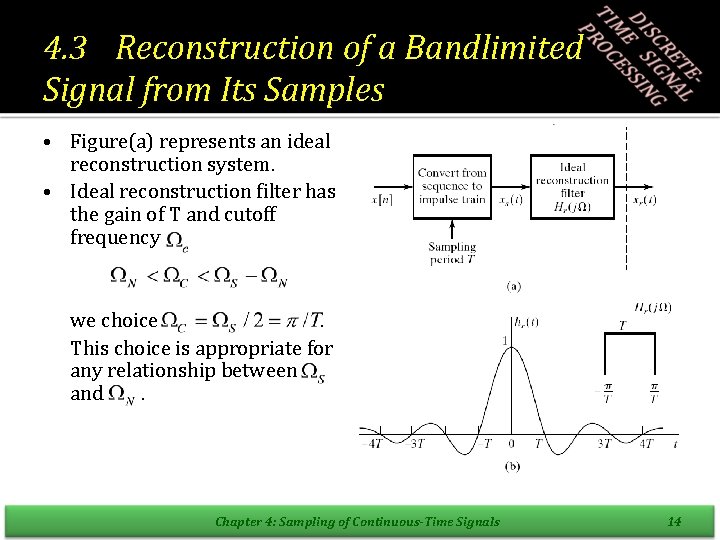
4. 3 Reconstruction of a Bandlimited Signal from Its Samples • Figure(a) represents an ideal reconstruction system. • Ideal reconstruction filter has the gain of T and cutoff frequency we choice. This choice is appropriate for any relationship between and. Chapter 4: Sampling of Continuous-Time Signals 14

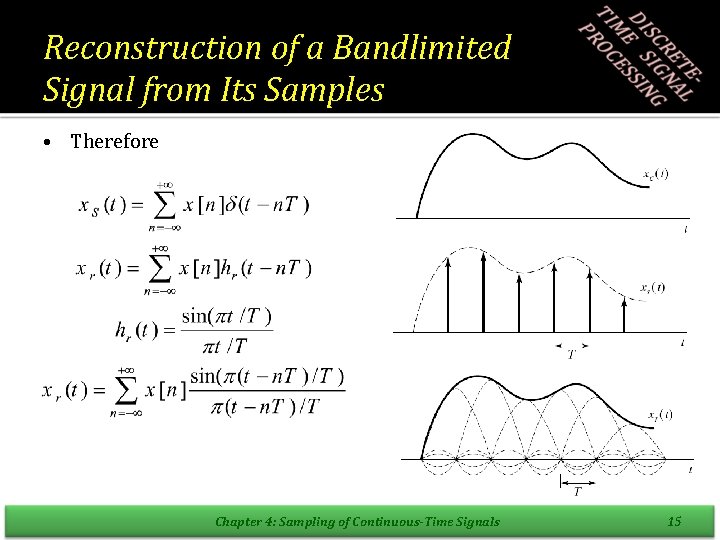
Reconstruction of a Bandlimited Signal from Its Samples • Therefore Chapter 4: Sampling of Continuous-Time Signals 15

Reconstruction of a Bandlimited Signal from Its Samples For all integer values of m. independent from the sampling period T. Therefore the resulting signal is an exact reconstruction of x c(t) at the sampling times. the fact that, if there is no aliasing, the low pass filter interpolates the correct reconstruction between the samples, and if there is aliasing, it can’t interpolate them correctly. Chapter 4: Sampling of Continuous-Time Signals 16

Ideal D/C Converter • The properties of the ideal D/C converter are most easily seen in the frequency domain. Chapter 4: Sampling of Continuous-Time Signals 17

4. 4 Discrete-Time Processing of Continuous-Time Signals • A major application of discrete-time systems is in the processing of continuous-time signals. We know from the previous sections Chapter 4: Sampling of Continuous-Time Signals 18

4. 4. 1 LTI Discrete-Time systems • In the LTI systems we have IF then Chapter 4: Sampling of Continuous-Time Signals 19

4. 4. 1 LTI Discrete-Time systems • In general if the discrete-time system is LTI and if the sampling frequency is above the Nyquist rate associated with the band width of the input xc(t), then the overall system will be equivalent to a LTI continuous-time system with an effective frequency response given by: Chapter 4: Sampling of Continuous-Time Signals 20

Example: Ideal Continuous-Time Lowpass Filtering Using a Discrete-Time Lowpass Filter Chapter 4: Sampling of Continuous-Time Signals 21

Example: Ideal Continuous-Time Lowpass Filtering Using a Discrete-Time Lowpass Filter Chapter 4: Sampling of Continuous-Time Signals 22

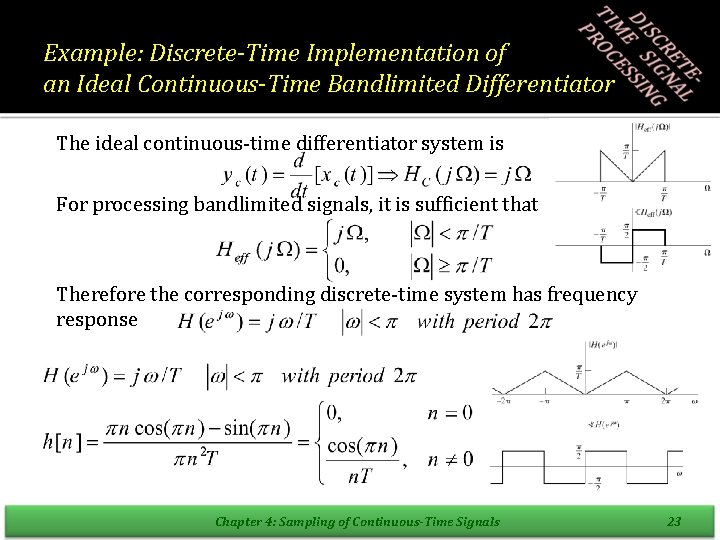
Example: Discrete-Time Implementation of an Ideal Continuous-Time Bandlimited Differentiator The ideal continuous-time differentiator system is For processing bandlimited signals, it is sufficient that Therefore the corresponding discrete-time system has frequency response Chapter 4: Sampling of Continuous-Time Signals 23

Example: Discrete-Time Implementation of an Ideal Continuous-Time Bandlimited Differentiator • If this system has the input Chapter 4: Sampling of Continuous-Time Signals 24

4. 4. 2 Impulse Invariance • If the desired continuous-time system has bandlimited frequency response then how to choose so that In this case the discrete-time system is said to be an impulseinvariant version of the continuous time system. Chapter 4: Sampling of Continuous-Time Signals 25

Example: A discrete-time lowpass filter obtained by impulse invariance • We want to obtain an ideal lowpass discrete-time filter with cutoff frequency. we can do this by sampling a continuous-time ideal lowpass filter with cutoff frequency Chapter 4: Sampling of Continuous-Time Signals 26

4. 6 Changing the sampling rate using discrete-time processing • We have seen that a continuous-time signal can be represented by a discrete-time signal. • It is often necessary to change the sampling rate of x[n] and obtain a new discrete-time signal such that • One approach is to reconstruct and then resample it with period , but it is of interest to consider methods that involve only discrete time operations. Chapter 4: Sampling of Continuous-Time Signals 27

4. 6. 1 Sampling rate reduction by an integer factor • Discrete-time sampler or compressor • If representation of then is an exact • Downsampling: the operation of reducing the sampling rate (including any filtering). Chapter 4: Sampling of Continuous-Time Signals 28

Frequency domain relation between the input and output of the compressor Chapter 4: Sampling of Continuous-Time Signals 29

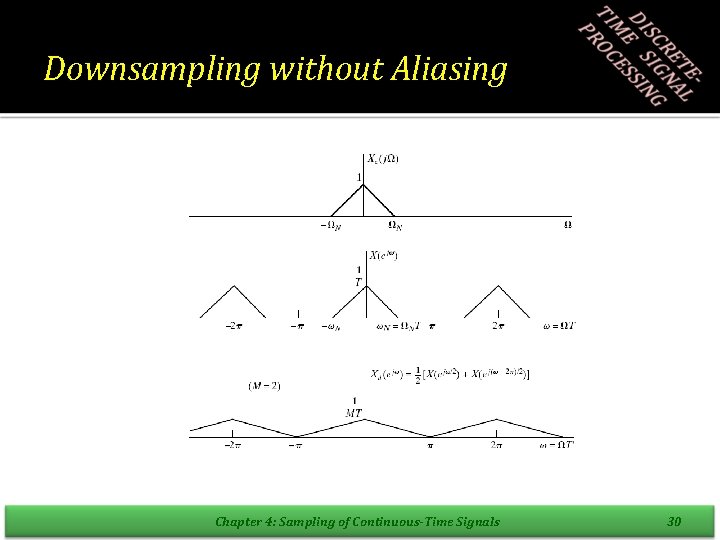
Downsampling without Aliasing Chapter 4: Sampling of Continuous-Time Signals 30

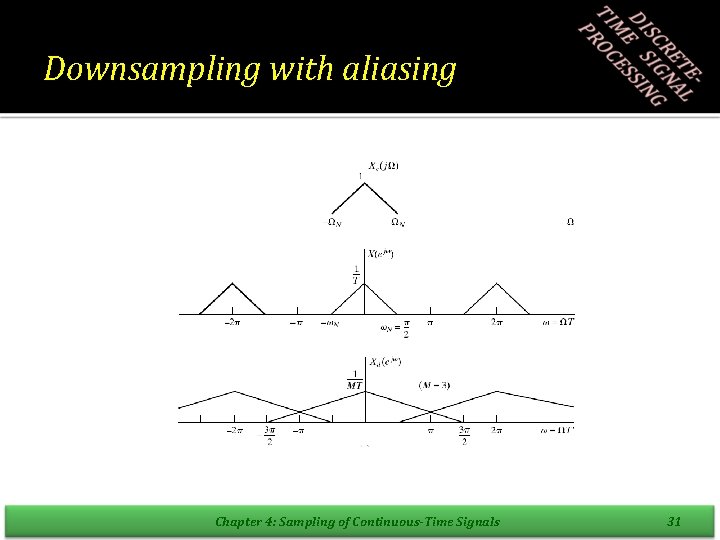
Downsampling with aliasing Chapter 4: Sampling of Continuous-Time Signals 31

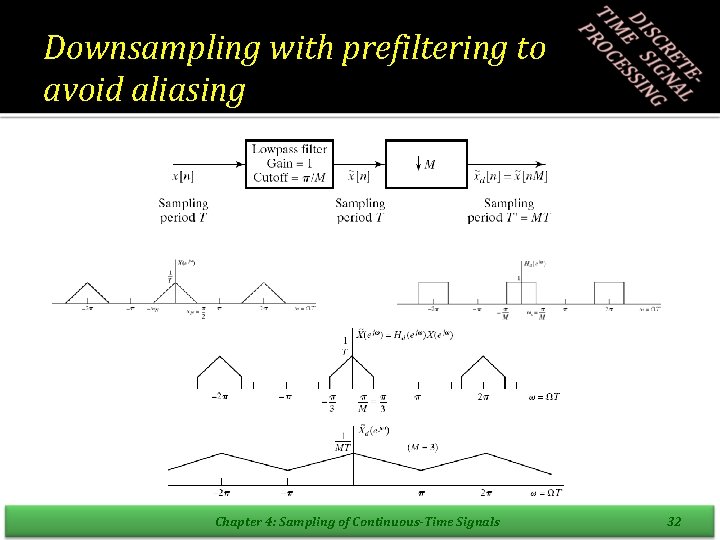
Downsampling with prefiltering to avoid aliasing Chapter 4: Sampling of Continuous-Time Signals 32

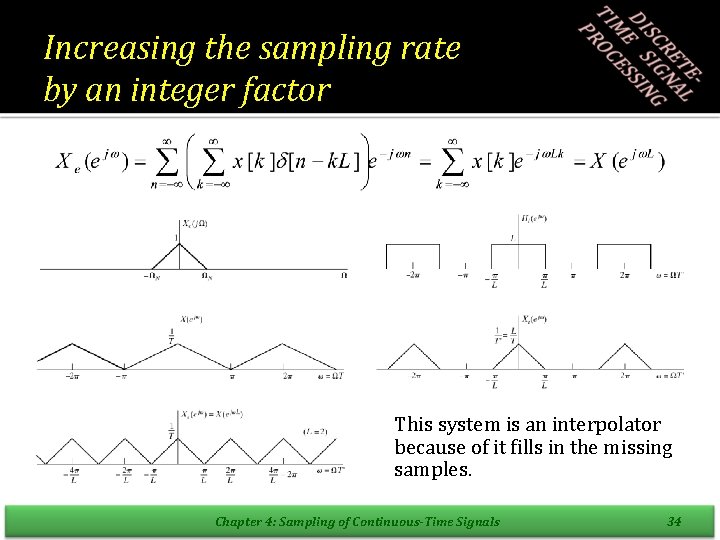
4. 6. 2 Increasing the sampling rate by an integer factor • We will refer to the operation of increasing the sampling rate upsampling • The system on the left is called a sampling rate expander. Its output is • The system on the right is a lowpass discrete-time filter with cutoff frequency and gain L. Chapter 4: Sampling of Continuous-Time Signals 33

Increasing the sampling rate by an integer factor This system is an interpolator because of it fills in the missing samples. Chapter 4: Sampling of Continuous-Time Signals 34

Increasing the Sampling Rate By an Integer Factor If the input sequence without aliasing then is obtained by oversampling of was obtained by sampling is correct for all n, And. Chapter 4: Sampling of Continuous-Time Signals 35

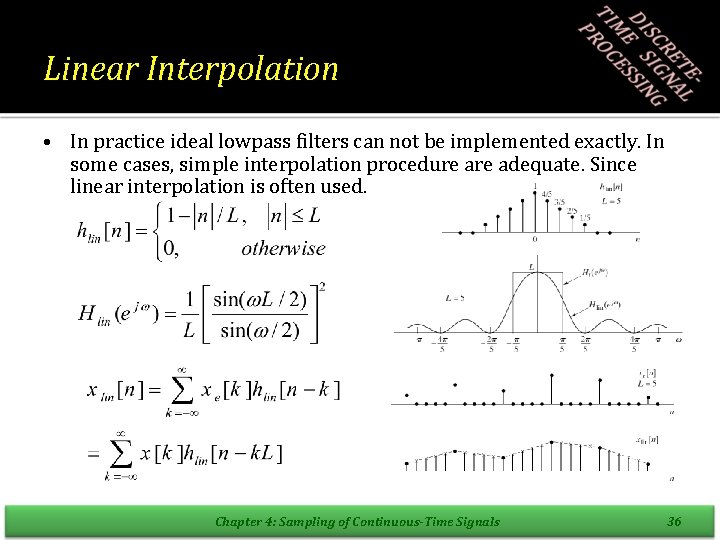
Linear Interpolation • In practice ideal lowpass filters can not be implemented exactly. In some cases, simple interpolation procedure adequate. Since linear interpolation is often used. Chapter 4: Sampling of Continuous-Time Signals 36

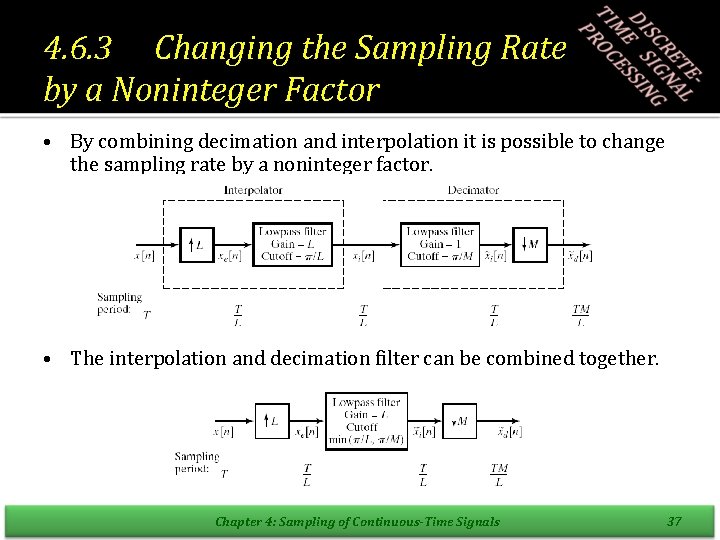
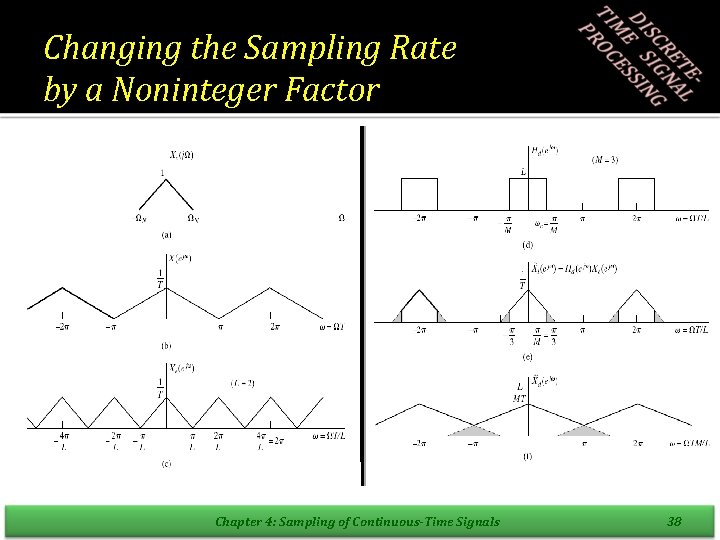
4. 6. 3 Changing the Sampling Rate by a Noninteger Factor • By combining decimation and interpolation it is possible to change the sampling rate by a noninteger factor. • The interpolation and decimation filter can be combined together. Chapter 4: Sampling of Continuous-Time Signals 37

Changing the Sampling Rate by a Noninteger Factor Chapter 4: Sampling of Continuous-Time Signals 38