Department of Computer and Information Science School of

Department of Computer and Information Science, School of Science, IUPUI CSCI 240 Analysis of Algorithms Big-Oh Dale Roberts, Lecturer Computer Science, IUPUI E-mail: droberts@cs. iupui. edu Dale Roberts

Asymptotic Analysis Ignoring constants in T(n) Analyzing T(n) as n "gets large" Example: The big-oh (O) Notation Dale Roberts

3 major notations Ο)g(n)), Big-Oh of g of n, the Asymptotic Upper Bound. W(g(n)), Big-Omega of g of n, the Asymptotic Lower Bound. Q(g(n)), Big-Theta of g of n, the Asymptotic Tight Bound. Dale Roberts

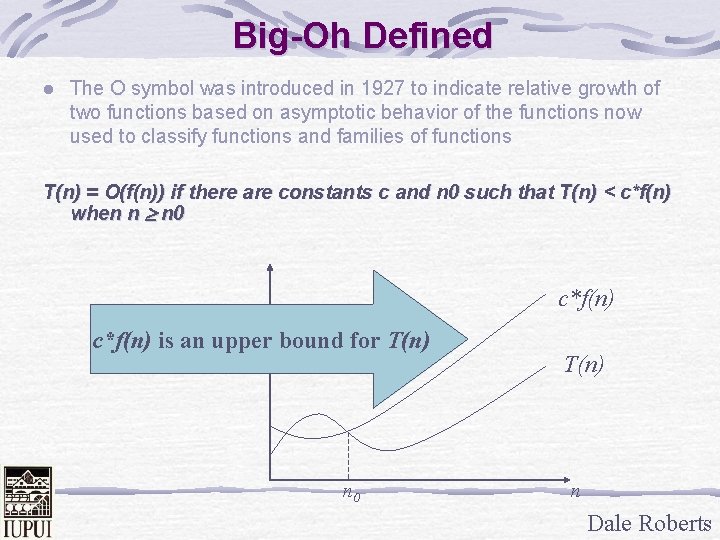
Big-Oh Defined l The O symbol was introduced in 1927 to indicate relative growth of two functions based on asymptotic behavior of the functions now used to classify functions and families of functions T(n) = O(f(n)) if there are constants c and n 0 such that T(n) < c*f(n) when n n 0 c*f(n) is an upper bound for T(n) n 0 T(n) n Dale Roberts

Big-Oh Describes an upper bound for the running time of an algorithm Upper bounds for Insertion Sort running times: • worst case: • best case: O(n 2) O(n) T(n) = c 1*n 2 + c 2*n + c 3 T(n) = c 1*n + c 2 Time Complexity Dale Roberts

Big-O Notation We say Insertion Sort’s run time is O(n 2) Properly we should say run time is in O(n 2) Read O as “Big-Oh” (you’ll also hear it as “order”) In general a function f(n) is O(g(n)) if there exist positive constants c and n 0 such that f(n) c g(n) for all n n 0 e. g. if f(n)=1000 n and g(n)=n 2, n 0 = 1000 and c = 1 then f(n) < 1*g(n) where n > n 0 and we say that f(n) = O(g(n(( The O notation indicates 'bounded above by a constant multiple of'. Dale Roberts

Big-Oh Properties Fastest growing function dominates a sum O(f(n)+g(n)) is O(max{f(n), g(n)}) Product of upper bounds is upper bound for the product If f is O(g) and h is O(r) then fh is O(gr) f is O(g) is transitive If f is O(g) and g is O(h) then f is O(h) Hierarchy of functions O(1), O(logn), O(n 1/2), O(nlogn), O(n 2), O(2 n), O(n!) Dale Roberts

Some Big-Oh’s are not reasonable Polynomial Time algorithms An algorithm is said to be polynomial if it is O( nc ), c >1 Polynomial algorithms are said to be reasonable They solve problems in reasonable times! Coefficients, constants or low-order terms are ignored e. g. if f(n) = 2 n 2 then f(n) = O(n 2( Exponential Time algorithms An algorithm is said to be exponential if it is O( rn ), r > 1 Exponential algorithms are said to be unreasonable Dale Roberts

Can we justify Big O notation? Big O notation is a huge simplification; can we justify it? It only makes sense for large problem sizes For sufficiently large problem sizes, the highest-order term swamps all the rest! Consider R = x 2 + 3 x + 5 as x varies: x x x = = = 0 x 2 100 x 2 10, 000 100, 000 = = 0 1000000 3 x 3 x = = 10 30 3000 5 5 = = 5 5 R R R = = = 5 135 10, 305 1, 003, 005 100, 030, 005 10, 000, 300, 005 Dale Roberts

Classifying Algorithms based on Big-Oh A function f(n) is said to be of at most logarithmic growth if f(n) = O(log n( A function f(n) is said to be of at most quadratic growth if f(n) = O(n 2( A function f(n) is said to be of at most polynomial growth if f(n) = O(nk), for some natural number k > 1 A function f(n) is said to be of at most exponential growth if there is a constant c, such that f(n) = O(cn), and c > 1 A function f(n) is said to be of at most factorial growth if f(n) = O(n. (! A function f(n) is said to have constant running time if the size of the input n has no effect on the running time of the algorithm (e. g. , assignment of a value to a variable). The equation for this algorithm is f(n) = c Other logarithmic classifications: f(n) = O(n log n( f(n) = O(log n( Dale Roberts

Rules for Calculating Big-Oh Base of Logs ignored logan = O(logbn( Power inside logs ignored log(n 2) = O(log n( Base and powers in exponents not ignored 3 n is not O(2 n( 2 a(n ) is not O(an( If T(x) is a polynomial of degree n, then T(x) = O(xn( Dale Roberts

Big-Oh Examples 1. 2 n 3 + 3 n 2 + n = 2 n 3 + 3 n 2 + O(n( 3 + O( n 2 + n ( 2 n = 3 + O( n 2( 2 n = = O(n 3 ) = O(n 4( 2 n. 23 + 3 n 2 + n = 2 n 3 + 3 n 2 + O(n( 3 + O(n 2 + n( 2 n = 3 + O(n 2) = O(n 3( 2 n = Dale Roberts

Big-Oh Examples (cont. ). 3 Suppose a program P is O(n 3), and a program Q is O(3 n), and that currently both can solve problems of size 50 in 1 hour. If the programs are run on another system that executes exactly 729 times as fast as the original system, what size problems will they be able to solve? Dale Roberts

Big-Oh Examples (cont) n 3 = 503 * 729 n = 50 * 9 = 450 3 n = 350 * 729 n = log 3 (729 * 350( n = log 3(729) + log 3 350 n = 6 + 50 = 56 Improvement: problem size increased by 9 times for n 3 algorithm but only a slight improvement in problem size (+6) for exponential algorithm. Dale Roberts

Acknowledgements Philadephia University, Jordan Nilagupta, Pradondet Dale Roberts