Density matrix and its application Density matrix An

Density matrix and its application

Density matrix • An alternative of state-vector (ket) representation for a certain set of state-vectors appearing with certain probabilities. 10/31/2020 2

Ensembles – pure and mixed states • Pure sate • Mixed state: set of pure quantum states with given probabilities • Mixing: weighting with classical probabilities • Superposition: weighting with quantum probability amplitudes • E. g. a pure sate can be a superposition 10/31/2020 3

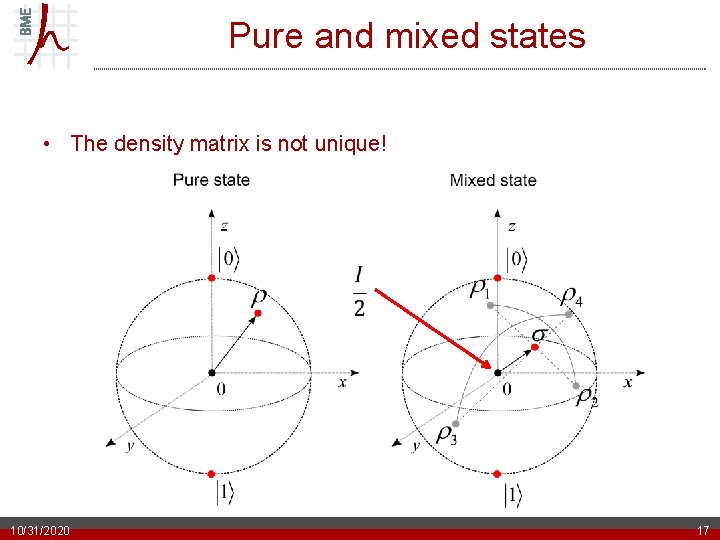
Are density matrices unique? • Density matrices are not unique. This is the price for being able to decompose entangled systems 10/31/2020 4

The Trace • where are the elements of the main diagonal • Eigenvalues and eigenvectors 10/31/2020 5

Properties of the Trace 10/31/2020 6

Trace- properties of density matrices • The trace of any density matrix is equal to one • for a pure state • for a mixed state • for a pure entangled system • for any mixed subsystem of an EPR pair 10/31/2020 7

2 nd Postulate (evolution) • The evolution of any closed physical system in time can be characterized by means of unitary transforms 10/31/2020 8

3 rd Postulate (measurement) • Any quantum measurement can be described bymeans of a set of measurement operators {Mm}, where m stands for the possible results of the measurement. The probability of measuring m if the system is in state v can be calculated as • and the system after measuring m gets in state 9

Illustration • Measurement basis: 10/31/2020 10

Decomposing a system - Partial trace • In general 10/31/2020 11

Decomposing a system - Partial trace • For product state systems 10/31/2020 12

Decomposing a system - Partial trace • For entangled systems 10/31/2020 pure! 13

10/31/2020 Max mixed! Contains no information 14

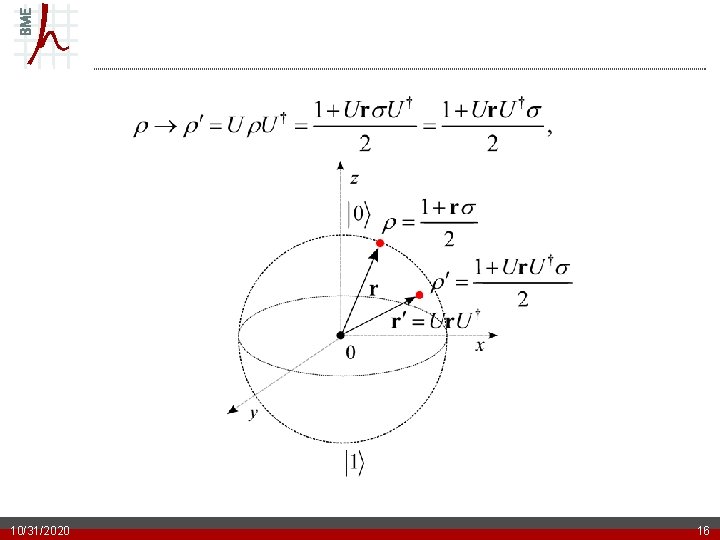
Geometrical interpretation of density matrices • Bloch sphere 10/31/2020 15

10/31/2020 16

Pure and mixed states • The density matrix is not unique! 10/31/2020 17